2024-2025学年北师大版数学八年级上册 综合测试卷(含答案)
文档属性
| 名称 | 2024-2025学年北师大版数学八年级上册 综合测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 00:00:00 | ||
图片预览


文档简介
综合测试卷
考试时间:120分钟 满分:120分
题号 — 二 三 总分
得分
一、选择题
1.下列命题中,真命题的个数是( )
①全等三角形的周长相等;②全等三角形的对应角相等;③全等三角形的面积相等;④全等三角形的对应角平分线相等.
A.4 B.3 C.2 D.1
2.若三角形的三个外角的度数比为2:3:4,则与之对应的三个内角的度数比是( )
A.4:3:2 B.3:2:4 C.5:3:1 D.3:1:5
3.下列图形中,已知 ,则可得到 的是( )
4.如图,直线 的顶点A 在直线n上, 若 则 ( )
5.如图,直线 ,点A在直线 上,以点A 为圆心,适当长度为半径画弧,分别交直线 于B,C两点,连接AC,BC,若 则 的大小为( )
6.如图所示,直线. ,FG平分 的度数是( )
7.一副三角板按如图所示的方式叠放在一起,则图中∠α的度数是( )
A.75° B.65° C.60° D.55°
8.如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°,则∠AOF 的度数是( )
A.20° B.25° C.30° D.35°
9.如图,在△ABC中,∠ABC和∠ACB 的平分线相交于点F,过点 F 作DE∥BC,交AB于点D,交AC于点E,若BD+CE=9,则线段DE的长是( )
A.9 B.8 C.7 D.6
10.如图,把△ABC纸片沿DE 折叠,当点A 落在四边形 BCDE 内部时,∠A 与∠1+∠2之间始终保持一种数量关系,此数量关系是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
二、填空题
11.把命题“对顶角相等”改写成“如果……,那么……”的形式:
12.如图,请填写一个条件,使结论成立:∵ ,∴a∥b.
13.已知:如图, ,则∠BCD= 度.
14.观察下列各式:……,请你将发现的规律用含自然数n(n≥1)的代数式表达出来:
三、解答题
15.(本题满分5分)判断下列命题的真假,若是假命题,请举出反例.
(1)若 则
(2)有一条边、两个角相等的两个三角形全等.
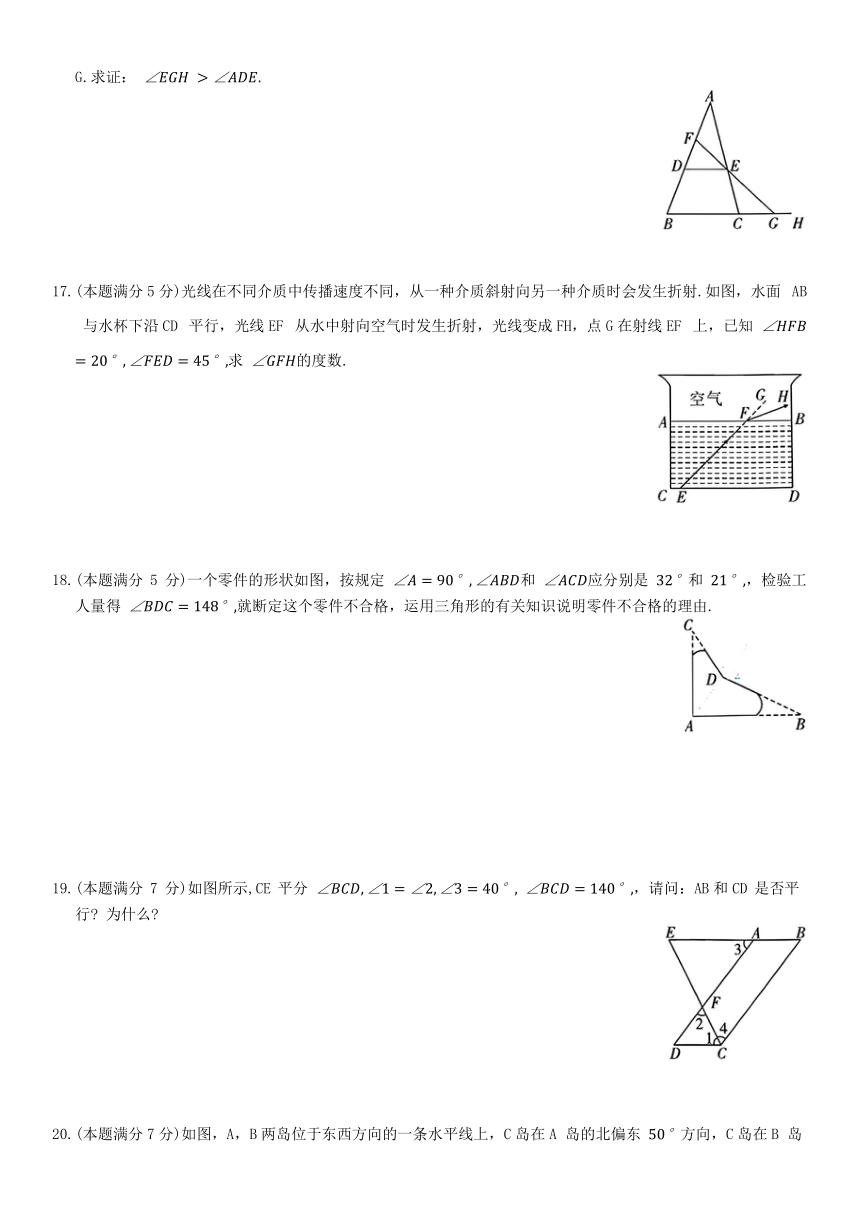
16.(本题满分5分)如图,已知点 D,E分别在AB,AC上, F是AD上一点,FE 的延长线交 BC 的延长线于点G.求证:
17.(本题满分5分)光线在不同介质中传播速度不同,从一种介质斜射向另一种介质时会发生折射.如图,水面 AB 与水杯下沿CD 平行,光线EF 从水中射向空气时发生折射,光线变成FH,点G在射线EF 上,已知 求 的度数.
18.(本题满分5分)一个零件的形状如图,按规定 和 应分别是 和 ,检验工人量得 就断定这个零件不合格,运用三角形的有关知识说明零件不合格的理由.
19.(本题满分 7 分)如图所示,CE 平分 ,请问:AB和CD 是否平行 为什么
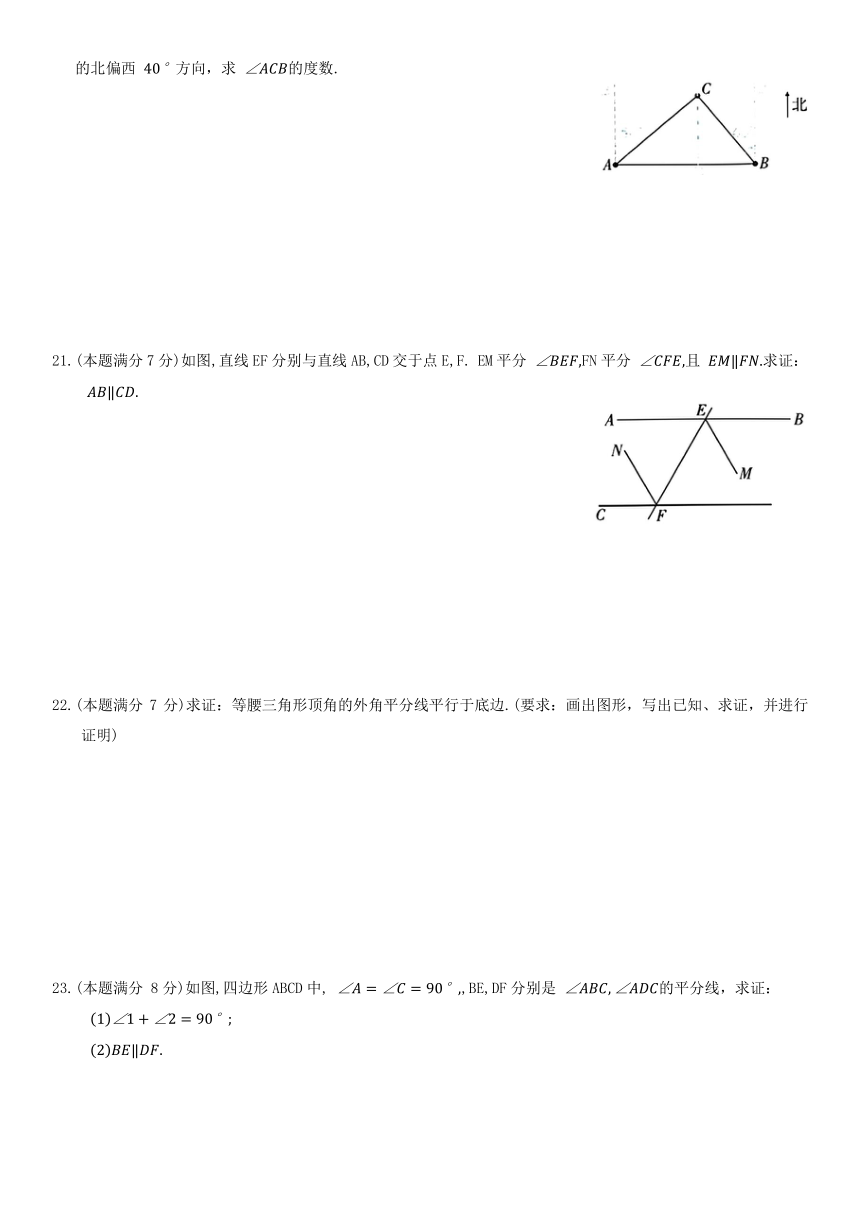
20.(本题满分7分)如图,A,B两岛位于东西方向的一条水平线上,C岛在A 岛的北偏东 方向,C岛在B 岛的北偏西 方向,求 的度数.
21.(本题满分7分)如图,直线EF分别与直线AB,CD交于点E,F. EM平分 FN平分 且 求证:
22.(本题满分7分)求证:等腰三角形顶角的外角平分线平行于底边.(要求:画出图形,写出已知、求证,并进行证明)
23.(本题满分 8分)如图,四边形ABCD中, ,BE,DF分别是 的平分线,求证:
24.(本题满分10分)如图所示, 是 的外角, BE平分 CE平分 ,BE、CE交于点E,求 的度数.
25.(本题满分12分)将一副直角三角板按图所示的方式放置, ,AB 边交直线DE 于点M,设 将直角三角板ABC绕着点C 旋转,在旋转过程中,点B 始终位于直线DE 下方,猜想变化过程中α与β的数量关系,并利用相交线与平行线的相关知识证明你的猜想.
综合测试卷
1、A 2、C 3、B 4.B 5.C 6.A 7.A 8.D 9.A10.B
11. 如果两个角是对顶角,那么这两个角相等 12.∵ ∠1=∠4 ,∴a∥b 13.30
14、
15.解:(1)假命题,x=--1,y=2时,2x+y=0.
(2)假命题,如图,△ABC 和△DEF中,AB=EF,∠B=∠E,∠A=∠D,则△ABC和△DEF不一定全等.
16.证明:∵DE∥BC,
∴∠ADE=∠B.
又∵∠EGH>∠B,
∴∠EGH>∠ADE.
17.解:∵AB∥CD,
∴∠GFB=∠FED=45°.
又∵∠HFB=20°,
∴∠GFH=∠GFB-∠HFB=45°-20°=25°.
18.解:如图,连接 AD 并延长,则∠1=∠ACD+∠CAD,∠2=∠ABD+∠BAD,
故∠BDC=
因为工人量得 所以此零件不合格.
19.解:AB和CD 平行.
理由:∵CE 平分∠BCD,
∴∠1=∠4.
又∵∠1=∠2,
∴∠2=∠4,
∴AD∥
∴∠3=∠D,
∴AB∥CD.
20解:如图,过点A,C,B分别画出南北方向的方向线,
由题意,得∠EAC=50°,∠FBC = 40°.
∵ AE∥DC∥BF,
∴∠ACD = ∠EAC = 50°,
∠BCD =
。
21.证明:∵ EM 平分∠BEF, FN 平分∠CFE,
∴∠BEF=2∠MEF,∠CFE=2∠NFE.
∵ EM ∥FN,
∴∠MEF =∠NFE,
∴ ∠BEF = ∠CFE,
∴ AB∥CD.
22.证明:已知:如图所示,在△ABC中,AB=AC,AD 为外角∠EAB 的平分线.
求证:AD∥BC.证明:∵AB=AC,AD为∠EAB 的平分线,
∴∠B=∠C,∠EAD=∠DAB.
∵∠B+∠C+∠BAC=180°,∠EAD+∠DAB+∠BAC=180°,
∴∠B+∠C=∠EAD+∠DAB,
∴∠B=∠DAB,∴AD∥BC.
23.证明:(1)∵BE,DF分别是∠ABC,∠ADC 的平分线,
∴∠1=∠ABE,∠2=∠ADF.
∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°.
∴2(∠1+∠2)=180°,
∴∠1+∠2=90°.
(2)在△FCD中,∵∠C=90°.
∴∠DFC+∠2=90.
∵∠1+∠2=90°,
∴∠1=∠DFC,
∴BE∥DF.
24.解:∵∠ACD=∠A+∠ABC,CE 平分∠ACD,
又∵∠ECD=∠E+∠EBC,
∴∠E+∠EBC= (∠A+∠ABC).
∵BE 平分
25.解:α与β的数量关系为α-β=15°或α+β=165°.
证明如下:当将直角三角板 ABC 绕着点C 顺时针旋转时,如图①,
∵∠BMD+∠B=∠BCE+∠DEC,
∴α+30°=β+45°,
∴α-β=15°.当将直角三角板 ABC绕着点C 逆时针旋转时,如图②,
∵∠BMD=∠1+∠B,而∠1=∠2,∠2=180°-∠DEC-∠BCE,
∴∠BMD=180°-∠DEC--∠BCE+∠B,
∴α=180°-45°-β+30°,
∴α+β=165°.
考试时间:120分钟 满分:120分
题号 — 二 三 总分
得分
一、选择题
1.下列命题中,真命题的个数是( )
①全等三角形的周长相等;②全等三角形的对应角相等;③全等三角形的面积相等;④全等三角形的对应角平分线相等.
A.4 B.3 C.2 D.1
2.若三角形的三个外角的度数比为2:3:4,则与之对应的三个内角的度数比是( )
A.4:3:2 B.3:2:4 C.5:3:1 D.3:1:5
3.下列图形中,已知 ,则可得到 的是( )
4.如图,直线 的顶点A 在直线n上, 若 则 ( )
5.如图,直线 ,点A在直线 上,以点A 为圆心,适当长度为半径画弧,分别交直线 于B,C两点,连接AC,BC,若 则 的大小为( )
6.如图所示,直线. ,FG平分 的度数是( )
7.一副三角板按如图所示的方式叠放在一起,则图中∠α的度数是( )
A.75° B.65° C.60° D.55°
8.如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°,则∠AOF 的度数是( )
A.20° B.25° C.30° D.35°
9.如图,在△ABC中,∠ABC和∠ACB 的平分线相交于点F,过点 F 作DE∥BC,交AB于点D,交AC于点E,若BD+CE=9,则线段DE的长是( )
A.9 B.8 C.7 D.6
10.如图,把△ABC纸片沿DE 折叠,当点A 落在四边形 BCDE 内部时,∠A 与∠1+∠2之间始终保持一种数量关系,此数量关系是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
二、填空题
11.把命题“对顶角相等”改写成“如果……,那么……”的形式:
12.如图,请填写一个条件,使结论成立:∵ ,∴a∥b.
13.已知:如图, ,则∠BCD= 度.
14.观察下列各式:……,请你将发现的规律用含自然数n(n≥1)的代数式表达出来:
三、解答题
15.(本题满分5分)判断下列命题的真假,若是假命题,请举出反例.
(1)若 则
(2)有一条边、两个角相等的两个三角形全等.
16.(本题满分5分)如图,已知点 D,E分别在AB,AC上, F是AD上一点,FE 的延长线交 BC 的延长线于点G.求证:
17.(本题满分5分)光线在不同介质中传播速度不同,从一种介质斜射向另一种介质时会发生折射.如图,水面 AB 与水杯下沿CD 平行,光线EF 从水中射向空气时发生折射,光线变成FH,点G在射线EF 上,已知 求 的度数.
18.(本题满分5分)一个零件的形状如图,按规定 和 应分别是 和 ,检验工人量得 就断定这个零件不合格,运用三角形的有关知识说明零件不合格的理由.
19.(本题满分 7 分)如图所示,CE 平分 ,请问:AB和CD 是否平行 为什么
20.(本题满分7分)如图,A,B两岛位于东西方向的一条水平线上,C岛在A 岛的北偏东 方向,C岛在B 岛的北偏西 方向,求 的度数.
21.(本题满分7分)如图,直线EF分别与直线AB,CD交于点E,F. EM平分 FN平分 且 求证:
22.(本题满分7分)求证:等腰三角形顶角的外角平分线平行于底边.(要求:画出图形,写出已知、求证,并进行证明)
23.(本题满分 8分)如图,四边形ABCD中, ,BE,DF分别是 的平分线,求证:
24.(本题满分10分)如图所示, 是 的外角, BE平分 CE平分 ,BE、CE交于点E,求 的度数.
25.(本题满分12分)将一副直角三角板按图所示的方式放置, ,AB 边交直线DE 于点M,设 将直角三角板ABC绕着点C 旋转,在旋转过程中,点B 始终位于直线DE 下方,猜想变化过程中α与β的数量关系,并利用相交线与平行线的相关知识证明你的猜想.
综合测试卷
1、A 2、C 3、B 4.B 5.C 6.A 7.A 8.D 9.A10.B
11. 如果两个角是对顶角,那么这两个角相等 12.∵ ∠1=∠4 ,∴a∥b 13.30
14、
15.解:(1)假命题,x=--1,y=2时,2x+y=0.
(2)假命题,如图,△ABC 和△DEF中,AB=EF,∠B=∠E,∠A=∠D,则△ABC和△DEF不一定全等.
16.证明:∵DE∥BC,
∴∠ADE=∠B.
又∵∠EGH>∠B,
∴∠EGH>∠ADE.
17.解:∵AB∥CD,
∴∠GFB=∠FED=45°.
又∵∠HFB=20°,
∴∠GFH=∠GFB-∠HFB=45°-20°=25°.
18.解:如图,连接 AD 并延长,则∠1=∠ACD+∠CAD,∠2=∠ABD+∠BAD,
故∠BDC=
因为工人量得 所以此零件不合格.
19.解:AB和CD 平行.
理由:∵CE 平分∠BCD,
∴∠1=∠4.
又∵∠1=∠2,
∴∠2=∠4,
∴AD∥
∴∠3=∠D,
∴AB∥CD.
20解:如图,过点A,C,B分别画出南北方向的方向线,
由题意,得∠EAC=50°,∠FBC = 40°.
∵ AE∥DC∥BF,
∴∠ACD = ∠EAC = 50°,
∠BCD =
。
21.证明:∵ EM 平分∠BEF, FN 平分∠CFE,
∴∠BEF=2∠MEF,∠CFE=2∠NFE.
∵ EM ∥FN,
∴∠MEF =∠NFE,
∴ ∠BEF = ∠CFE,
∴ AB∥CD.
22.证明:已知:如图所示,在△ABC中,AB=AC,AD 为外角∠EAB 的平分线.
求证:AD∥BC.证明:∵AB=AC,AD为∠EAB 的平分线,
∴∠B=∠C,∠EAD=∠DAB.
∵∠B+∠C+∠BAC=180°,∠EAD+∠DAB+∠BAC=180°,
∴∠B+∠C=∠EAD+∠DAB,
∴∠B=∠DAB,∴AD∥BC.
23.证明:(1)∵BE,DF分别是∠ABC,∠ADC 的平分线,
∴∠1=∠ABE,∠2=∠ADF.
∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°.
∴2(∠1+∠2)=180°,
∴∠1+∠2=90°.
(2)在△FCD中,∵∠C=90°.
∴∠DFC+∠2=90.
∵∠1+∠2=90°,
∴∠1=∠DFC,
∴BE∥DF.
24.解:∵∠ACD=∠A+∠ABC,CE 平分∠ACD,
又∵∠ECD=∠E+∠EBC,
∴∠E+∠EBC= (∠A+∠ABC).
∵BE 平分
25.解:α与β的数量关系为α-β=15°或α+β=165°.
证明如下:当将直角三角板 ABC 绕着点C 顺时针旋转时,如图①,
∵∠BMD+∠B=∠BCE+∠DEC,
∴α+30°=β+45°,
∴α-β=15°.当将直角三角板 ABC绕着点C 逆时针旋转时,如图②,
∵∠BMD=∠1+∠B,而∠1=∠2,∠2=180°-∠DEC-∠BCE,
∴∠BMD=180°-∠DEC--∠BCE+∠B,
∴α=180°-45°-β+30°,
∴α+β=165°.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
