2024-2025学年北师大版数学八年级上册 期末测试卷(含答案)
文档属性
| 名称 | 2024-2025学年北师大版数学八年级上册 期末测试卷(含答案) | 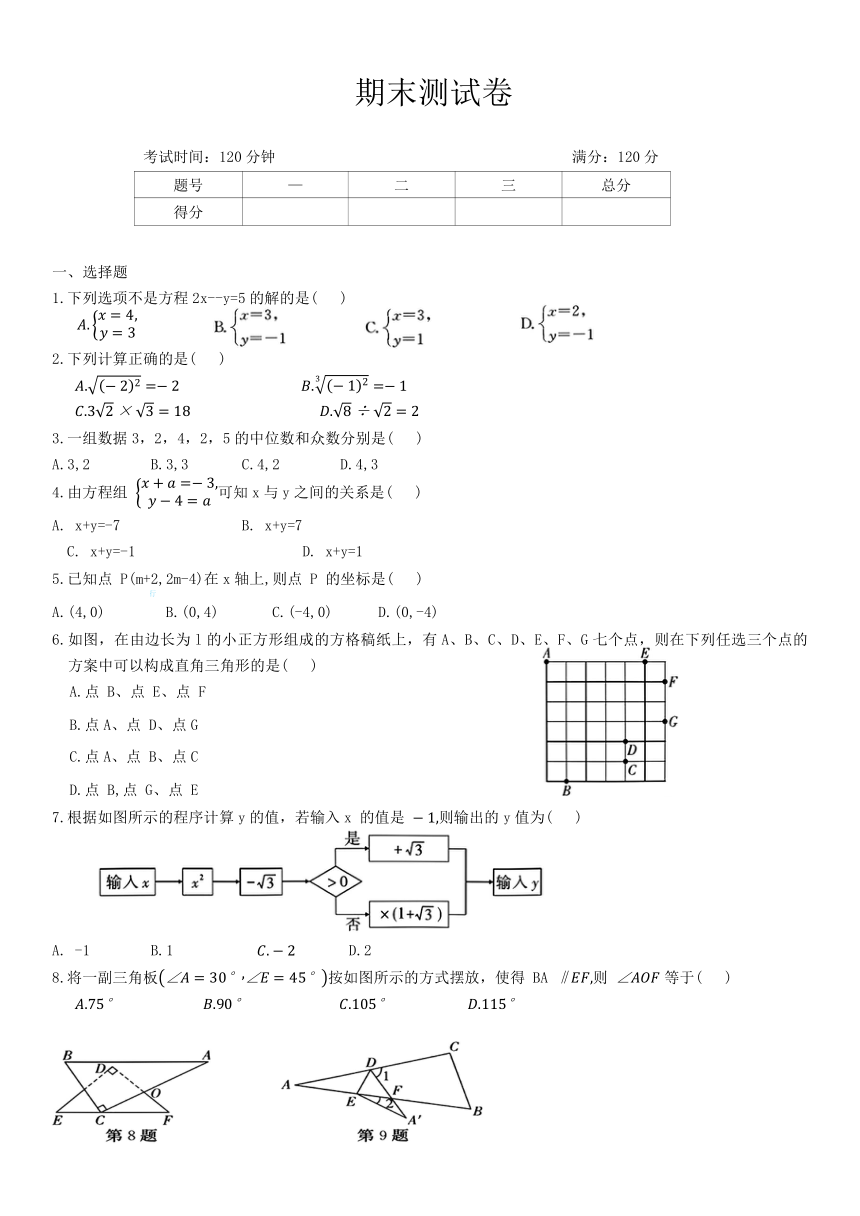 | |
| 格式 | docx | ||
| 文件大小 | 884.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 13:49:37 | ||
图片预览




文档简介
期末测试卷
考试时间:120分钟 满分:120分
题号 — 二 三 总分
得分
一、选择题
1.下列选项不是方程2x--y=5的解的是( )
2.下列计算正确的是( )
3.一组数据3,2,4,2,5的中位数和众数分别是( )
A.3,2 B.3,3 C.4,2 D.4,3
4.由方程组 可知x与y之间的关系是( )
A. x+y=-7 B. x+y=7
C. x+y=-1 D. x+y=1
5.已知点 P(m+2,2m-4)在x轴上,则点 P 的坐标是( )
A.(4,0) B.(0,4) C.(-4,0) D.(0,-4)
6.如图,在由边长为l的小正方形组成的方格稿纸上,有A、B、C、D、E、F、G七个点,则在下列任选三个点的方案中可以构成直角三角形的是( )
A.点 B、点 E、点 F
B.点A、点 D、点G
C.点A、点 B、点C
D.点 B,点 G、点 E
7.根据如图所示的程序计算y的值,若输入x 的值是 则输出的y值为( )
A. -1 B.1 D.2
8.将一副三角板按如图所示的方式摆放,使得 BA 则 等于( )
9.如图,将纸片△ABC沿DE 折叠,使点 A 落在点A'处,若∠1=80°,∠2=24°,则∠A为( )
A.24° B.28° C.32° D.36°
10.一次函数. 与y =x+a的图象如图所示,则下列结论:①k<0;②ab>0;③当x<3时,y 随x的增大而增大;④当x<3时,yA.1个 B.2个
C.3个 D.4个
二填空题、
11.写出一个满足 的整数a的值: .
12.评定学生的学科期末成绩由考试分数、作业分数、课堂参与分数三部分组成,并按3:2:5的比例确定,已知小新的数学考试90分,作业95分,课堂参与92分,则他的数学期末成绩为 分.
13.已知点A(2a-b,b-a),点 B(a,b),直线 AB与x轴平行,且线段AB的长为3,则b-a的 .
14.如图,架在消防车上的云梯 AB 的长为 10m,∠ADB=90°,AD=2BD,云梯底部离地面的距离 BC为2m,则云梯的顶端离地面的距离AE为 m.
三、解答题
15.(本题满分5分)计算:
(本题满分5分)解方程组:
17.(本题满分5分)如图所示,已知 于点E,求 的度数.
18.(本题满分5分)如图,在由边长为1的小正方形组成的( 的网格中,给出了以格点(网格线的交点)为端点的线段AB.
(1)在网格中,以AB 为直角边作直角三角形ABC,使得斜边. 且点C在格点上.
(2)△ABC的面积是 ,斜边AC上的高的长度是——— . .
19.(本题满分7分)如图,数轴的正半轴上有A、B、C三点,表示1和 的对应点分别为A、B,点B 到点A 的距离与点C 到原点的距离相等,设点C所表示的数为x.
(1)x的值为 .
(2)求. 的值,并写出. 的平方根.
20.(本题满分7分)为推广黄冈各县市名优农产品,市政府组织创办了“黄冈地标馆”.一顾客在“黄冈地标馆”发现,如果购买6 盒羊角春牌绿茶和4盒九孔牌藕粉,共需960元.如果购买1盒羊角春牌绿茶和3盒九孔牌藕粉共需300元.请问每盒羊角春牌绿茶和每盒九孔牌藕粉分别需要多少元.
21.(本题满分7分)甲、乙两车在笔直的公路上同起点、同方向、同终点匀速行驶720km.先到终点的原地休息,已知甲车先出发2h,在整个过程中,甲、乙两车的距离 y( km)与甲车出发的时间(h)之间的关系如图所示.
(1)甲车的速度为 km/h,乙车的速度为 km/h.
(2)求出线段AB所在直线的函数关系式,并写出x的取值范围.
22.(本题满分7分)如图,已知点 E、F在直线AB 上,点G在线段CD上,ED与FG 交于点H,
(1)求证:
(2)若 求 的度数.
23.(本题满分8分)如图,在正方形网格中,已知点 A 的坐标是(1,1),点B的坐标是(2,0).
(1)在图中建立平面直角坐标系;
(2)图中点C的坐标是 ,点C关于x 轴的对称点( 的坐标是 ;
(3)若点 D的坐标为( ,在图中标出点 D的位置;
(4)在(2)的条件下,将点 B 向左平移3个单位长度,再向上平移1个单位长度得到点. ,那么点 的坐标是 .△AB'C'的面积为 .
24.(本题满分10分)为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量为每袋500g,与之相差大于10g为不合格.为检验分装效果,工厂对这两台机器分装的成品进行了抽样和分析,过程如下:
【收集数据】 从甲、乙两台机器分装的成品中各随机抽取20袋,测得实际质量(单位:g)如下:
甲:501 497 498 502 513 489 506 490 505 486
502 503 498 497 491 500 505 502 504 505
乙:505 499 502 491 487 506 493 505 499 498
502 503 501 490 501 502 511 499 499 501
【整理数据】 整理以上数据,得到每袋质量x(g)的频数分布表.
机器 质量
485≤ x<490 490≤ x<495 495≤ x<500 500≤ x<505 505≤ x<510 510≤ x<515
甲 2 2 4 7 4 1
乙 1 3 5 7 3 1
【分析数据】 根据以上数据,得到以下统计量.
机器 统计量
平均数 中位数 方差 不合格率
甲 499.7 501.5 42.01 b
乙 499.7 a 31.81 10%
根据以上信息,回答下列问题.
(1)表格中的
(2)综合上表中的统计量,判断工厂应选购哪一台分装机,并说明理由.
25.(本题满分12分)定义:在平面直角坐标系中,对于任意两点 y ),Q(x ,y ),若点 T(x,y)满足 那么称点 T是点P,Q的阳光点.例如:P(-1,6),Q(5,2),当点 T(x,y)满足. 时,点 T(1,2)是点 P,Q的阳光点.
(1)已知点A(0,b),B(4,0),点C是点A,B的阳光点.
①当b=4时,求点C的坐标;
②当b=-4时,求直线AB的函数表达式,并判断此时点C是否在直线 AB 上.
(2)已知点 D(3,0),点. 是直线l上任意一点,点T(x,y)是点D,E的阳光点.
①试确定 y与x之间的函数表达式;
②在如图所示的平面直角坐标系中,画出①中所求的函数图象,并写出该函数的两条性质.
期末测试卷
1.B 2.D 3.A 4.D 5.A 6.A 7.C 8.A 9.B 10.B
11. 4 12. 92 13.±3 14. 4+2
15.解:原式
16.解:方程组整理得+②得,n=1,把n=1代入①,得 则方程组的解为
17.解:
∠D=73°.
又∵FD⊥BC 于点 E,
中.
18.解:(1)如图所示.
的面积是 3 ,斜边 AC上的高的长度是
19.(1)x的值为
(2)解: 2.
因为2 的平方根是
所以 2)的平方根是
20.解:设每盒羊角春牌绿茶x元,每盒九孔牌藕粉y元,
依题意可列方程组解得
即每盒羊角春牌绿茶 120 元,每盒九孔牌藕粉60元.
21.(1)甲车的速度为 60 km/h,乙车的速度为 80 km/h.
(2)解:由题意知点A(11,60),甲再行60÷60=1(h)到达终点,
点B 坐标为(12,0).
设线段AB 所在直线的函数关系式为y= kx+b,
把点A(11,60),点B ( 12, 0 ) 代 入, 得
解得k=-60,b=720,所以y=-60x+720,11≤x≤12.
22.(1)证明:∵∠CED=∠GHD,
∴CE∥FG.
∴∠C=∠FGD,
∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD.
(2)解:由(1)知,∵CE∥FG,又∠EHF=∠GHD=75°,
∴∠CED=∠GHD=75°,
∵AB∥CD,∠D=45°.
∴∠HEF=∠D=45°,
∴∠AEM=∠CEF=∠CED+
23.解:(1)平面直角坐标系如图所示.
(2)图中点C的坐标是 ,点C关于x轴的对称点 的坐标是
(3)点 D 的位置如图所示.
(4)在(2)的条件下,将点 B 向左平移3个单位长度,再向上平移1个单位长度得到点 ,那么点. 的坐标是 的面积为 1 .
24.(1)表格中的a= 501 ,b= 15% .
(2)解:工厂应选购乙分装机.
理由:比较甲、乙两台机器的统计量可知,甲与乙的平均数相同,
中位数相差不大,乙的方差较小,且不合格率更低.
以上分析说明,乙机器的分装合格率更高,且稳定性更好,
所以,乙机器的分装效果更好,工厂应选购乙机器.
25.解:
C点坐标(1,1)
②b=--4时,
C点坐标(1,-1).设直线AB 的函数表达式为y= kx+b,
将点A(0,-4),点B(4,0)代入得 得
所以直线AB 的函数表达式为. x--4.当x=1时,x-4=1-4=-3≠-1,
所以C点不在直线AB 上.
(2)①由阳光点定义得
由①得t=4x-3,由②得t=2y-1.
所以4x-3=2y-1,即y=2x-1,
即y与x之间的函数表达式为y=2x-1.
②如图所示;性质1:y随x的增大而增大 性质2:该图象与y轴交于点(0,-1).
考试时间:120分钟 满分:120分
题号 — 二 三 总分
得分
一、选择题
1.下列选项不是方程2x--y=5的解的是( )
2.下列计算正确的是( )
3.一组数据3,2,4,2,5的中位数和众数分别是( )
A.3,2 B.3,3 C.4,2 D.4,3
4.由方程组 可知x与y之间的关系是( )
A. x+y=-7 B. x+y=7
C. x+y=-1 D. x+y=1
5.已知点 P(m+2,2m-4)在x轴上,则点 P 的坐标是( )
A.(4,0) B.(0,4) C.(-4,0) D.(0,-4)
6.如图,在由边长为l的小正方形组成的方格稿纸上,有A、B、C、D、E、F、G七个点,则在下列任选三个点的方案中可以构成直角三角形的是( )
A.点 B、点 E、点 F
B.点A、点 D、点G
C.点A、点 B、点C
D.点 B,点 G、点 E
7.根据如图所示的程序计算y的值,若输入x 的值是 则输出的y值为( )
A. -1 B.1 D.2
8.将一副三角板按如图所示的方式摆放,使得 BA 则 等于( )
9.如图,将纸片△ABC沿DE 折叠,使点 A 落在点A'处,若∠1=80°,∠2=24°,则∠A为( )
A.24° B.28° C.32° D.36°
10.一次函数. 与y =x+a的图象如图所示,则下列结论:①k<0;②ab>0;③当x<3时,y 随x的增大而增大;④当x<3时,y
C.3个 D.4个
二填空题、
11.写出一个满足 的整数a的值: .
12.评定学生的学科期末成绩由考试分数、作业分数、课堂参与分数三部分组成,并按3:2:5的比例确定,已知小新的数学考试90分,作业95分,课堂参与92分,则他的数学期末成绩为 分.
13.已知点A(2a-b,b-a),点 B(a,b),直线 AB与x轴平行,且线段AB的长为3,则b-a的 .
14.如图,架在消防车上的云梯 AB 的长为 10m,∠ADB=90°,AD=2BD,云梯底部离地面的距离 BC为2m,则云梯的顶端离地面的距离AE为 m.
三、解答题
15.(本题满分5分)计算:
(本题满分5分)解方程组:
17.(本题满分5分)如图所示,已知 于点E,求 的度数.
18.(本题满分5分)如图,在由边长为1的小正方形组成的( 的网格中,给出了以格点(网格线的交点)为端点的线段AB.
(1)在网格中,以AB 为直角边作直角三角形ABC,使得斜边. 且点C在格点上.
(2)△ABC的面积是 ,斜边AC上的高的长度是——— . .
19.(本题满分7分)如图,数轴的正半轴上有A、B、C三点,表示1和 的对应点分别为A、B,点B 到点A 的距离与点C 到原点的距离相等,设点C所表示的数为x.
(1)x的值为 .
(2)求. 的值,并写出. 的平方根.
20.(本题满分7分)为推广黄冈各县市名优农产品,市政府组织创办了“黄冈地标馆”.一顾客在“黄冈地标馆”发现,如果购买6 盒羊角春牌绿茶和4盒九孔牌藕粉,共需960元.如果购买1盒羊角春牌绿茶和3盒九孔牌藕粉共需300元.请问每盒羊角春牌绿茶和每盒九孔牌藕粉分别需要多少元.
21.(本题满分7分)甲、乙两车在笔直的公路上同起点、同方向、同终点匀速行驶720km.先到终点的原地休息,已知甲车先出发2h,在整个过程中,甲、乙两车的距离 y( km)与甲车出发的时间(h)之间的关系如图所示.
(1)甲车的速度为 km/h,乙车的速度为 km/h.
(2)求出线段AB所在直线的函数关系式,并写出x的取值范围.
22.(本题满分7分)如图,已知点 E、F在直线AB 上,点G在线段CD上,ED与FG 交于点H,
(1)求证:
(2)若 求 的度数.
23.(本题满分8分)如图,在正方形网格中,已知点 A 的坐标是(1,1),点B的坐标是(2,0).
(1)在图中建立平面直角坐标系;
(2)图中点C的坐标是 ,点C关于x 轴的对称点( 的坐标是 ;
(3)若点 D的坐标为( ,在图中标出点 D的位置;
(4)在(2)的条件下,将点 B 向左平移3个单位长度,再向上平移1个单位长度得到点. ,那么点 的坐标是 .△AB'C'的面积为 .
24.(本题满分10分)为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量为每袋500g,与之相差大于10g为不合格.为检验分装效果,工厂对这两台机器分装的成品进行了抽样和分析,过程如下:
【收集数据】 从甲、乙两台机器分装的成品中各随机抽取20袋,测得实际质量(单位:g)如下:
甲:501 497 498 502 513 489 506 490 505 486
502 503 498 497 491 500 505 502 504 505
乙:505 499 502 491 487 506 493 505 499 498
502 503 501 490 501 502 511 499 499 501
【整理数据】 整理以上数据,得到每袋质量x(g)的频数分布表.
机器 质量
485≤ x<490 490≤ x<495 495≤ x<500 500≤ x<505 505≤ x<510 510≤ x<515
甲 2 2 4 7 4 1
乙 1 3 5 7 3 1
【分析数据】 根据以上数据,得到以下统计量.
机器 统计量
平均数 中位数 方差 不合格率
甲 499.7 501.5 42.01 b
乙 499.7 a 31.81 10%
根据以上信息,回答下列问题.
(1)表格中的
(2)综合上表中的统计量,判断工厂应选购哪一台分装机,并说明理由.
25.(本题满分12分)定义:在平面直角坐标系中,对于任意两点 y ),Q(x ,y ),若点 T(x,y)满足 那么称点 T是点P,Q的阳光点.例如:P(-1,6),Q(5,2),当点 T(x,y)满足. 时,点 T(1,2)是点 P,Q的阳光点.
(1)已知点A(0,b),B(4,0),点C是点A,B的阳光点.
①当b=4时,求点C的坐标;
②当b=-4时,求直线AB的函数表达式,并判断此时点C是否在直线 AB 上.
(2)已知点 D(3,0),点. 是直线l上任意一点,点T(x,y)是点D,E的阳光点.
①试确定 y与x之间的函数表达式;
②在如图所示的平面直角坐标系中,画出①中所求的函数图象,并写出该函数的两条性质.
期末测试卷
1.B 2.D 3.A 4.D 5.A 6.A 7.C 8.A 9.B 10.B
11. 4 12. 92 13.±3 14. 4+2
15.解:原式
16.解:方程组整理得+②得,n=1,把n=1代入①,得 则方程组的解为
17.解:
∠D=73°.
又∵FD⊥BC 于点 E,
中.
18.解:(1)如图所示.
的面积是 3 ,斜边 AC上的高的长度是
19.(1)x的值为
(2)解: 2.
因为2 的平方根是
所以 2)的平方根是
20.解:设每盒羊角春牌绿茶x元,每盒九孔牌藕粉y元,
依题意可列方程组解得
即每盒羊角春牌绿茶 120 元,每盒九孔牌藕粉60元.
21.(1)甲车的速度为 60 km/h,乙车的速度为 80 km/h.
(2)解:由题意知点A(11,60),甲再行60÷60=1(h)到达终点,
点B 坐标为(12,0).
设线段AB 所在直线的函数关系式为y= kx+b,
把点A(11,60),点B ( 12, 0 ) 代 入, 得
解得k=-60,b=720,所以y=-60x+720,11≤x≤12.
22.(1)证明:∵∠CED=∠GHD,
∴CE∥FG.
∴∠C=∠FGD,
∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD.
(2)解:由(1)知,∵CE∥FG,又∠EHF=∠GHD=75°,
∴∠CED=∠GHD=75°,
∵AB∥CD,∠D=45°.
∴∠HEF=∠D=45°,
∴∠AEM=∠CEF=∠CED+
23.解:(1)平面直角坐标系如图所示.
(2)图中点C的坐标是 ,点C关于x轴的对称点 的坐标是
(3)点 D 的位置如图所示.
(4)在(2)的条件下,将点 B 向左平移3个单位长度,再向上平移1个单位长度得到点 ,那么点. 的坐标是 的面积为 1 .
24.(1)表格中的a= 501 ,b= 15% .
(2)解:工厂应选购乙分装机.
理由:比较甲、乙两台机器的统计量可知,甲与乙的平均数相同,
中位数相差不大,乙的方差较小,且不合格率更低.
以上分析说明,乙机器的分装合格率更高,且稳定性更好,
所以,乙机器的分装效果更好,工厂应选购乙机器.
25.解:
C点坐标(1,1)
②b=--4时,
C点坐标(1,-1).设直线AB 的函数表达式为y= kx+b,
将点A(0,-4),点B(4,0)代入得 得
所以直线AB 的函数表达式为. x--4.当x=1时,x-4=1-4=-3≠-1,
所以C点不在直线AB 上.
(2)①由阳光点定义得
由①得t=4x-3,由②得t=2y-1.
所以4x-3=2y-1,即y=2x-1,
即y与x之间的函数表达式为y=2x-1.
②如图所示;性质1:y随x的增大而增大 性质2:该图象与y轴交于点(0,-1).
同课章节目录
