6.6余角和补角 课件(共20张PPT) 青岛版(2024)数学七年级上册
文档属性
| 名称 | 6.6余角和补角 课件(共20张PPT) 青岛版(2024)数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 671.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 19:34:27 | ||
图片预览




文档简介
(共20张PPT)
第6章
基本的几何图形
6.6 余角和补角
1、理解余角和补角的概念,会判断两个角的互余和互补关系。
2、探索并掌握同角或等角的余角相等、同角或等角的补角相等的性质的运算及解决一些实际问题。
学习目标
任务一、互余、互补定义
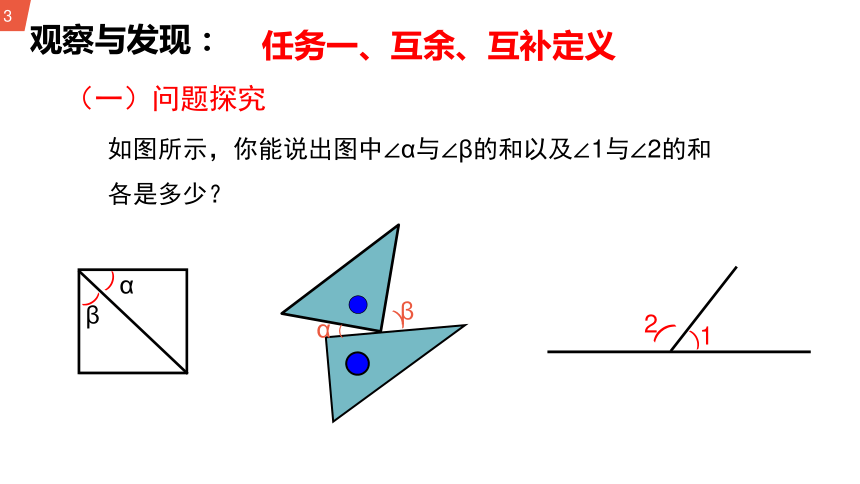
(一)问题探究
如图所示,你能说出图中∠α与∠β的和以及∠1与∠2的和各是多少?
)
)
α
β
α
β
)
)
1
2
)
)
观察与发现:
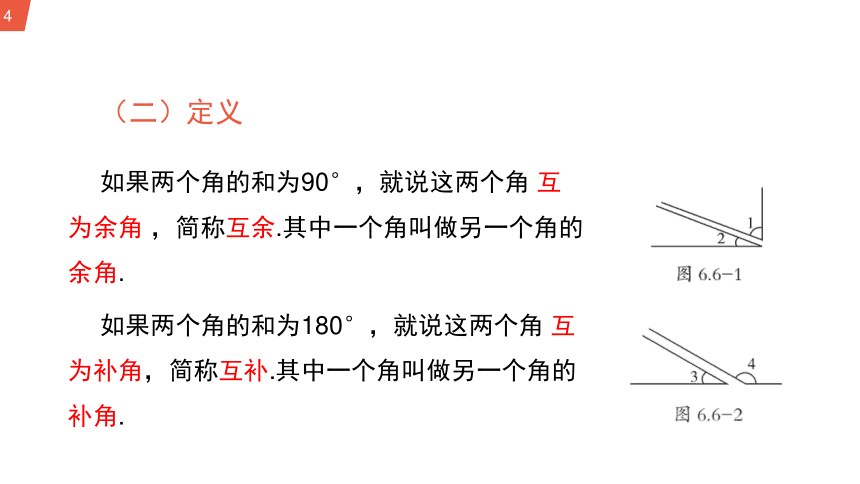
(二)定义
如果两个角的和为90°,就说这两个角 互为余角 ,简称互余.其中一个角叫做另一个角的余角.
如果两个角的和为180°,就说这两个角 互为补角,简称互补.其中一个角叫做另一个角的补角.
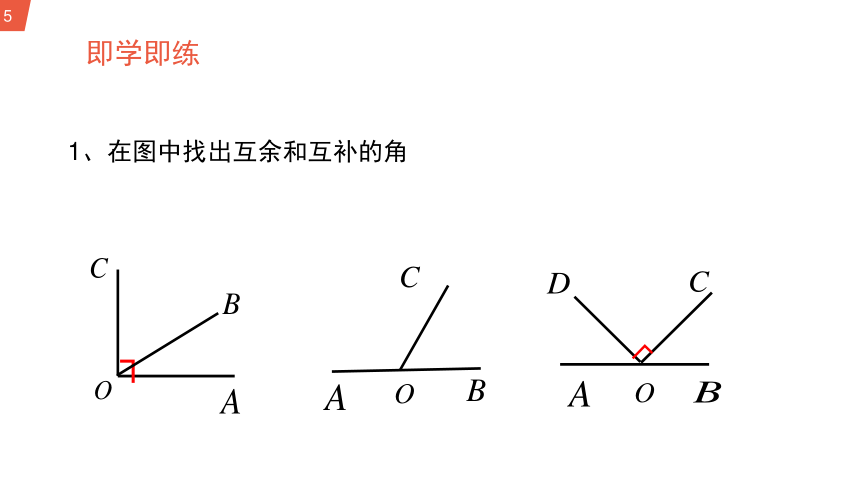
即学即练
1、在图中找出互余和互补的角
┐
┌
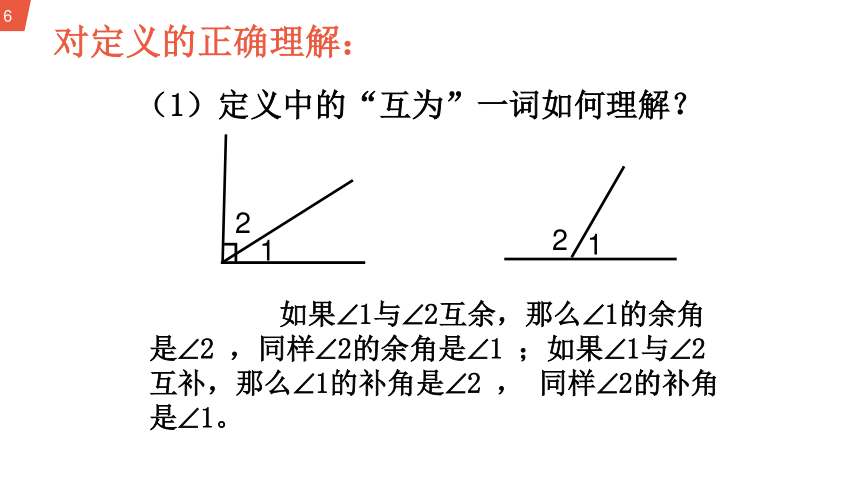
对定义的正确理解:
(1)定义中的“互为”一词如何理解?
如果 1与 2互余,那么 1的余角是 2 ,同样 2的余角是 1 ;如果 1与 2互补,那么 1的补角是 2 , 同样 2的补角是 1。
┐
1
2
1
2
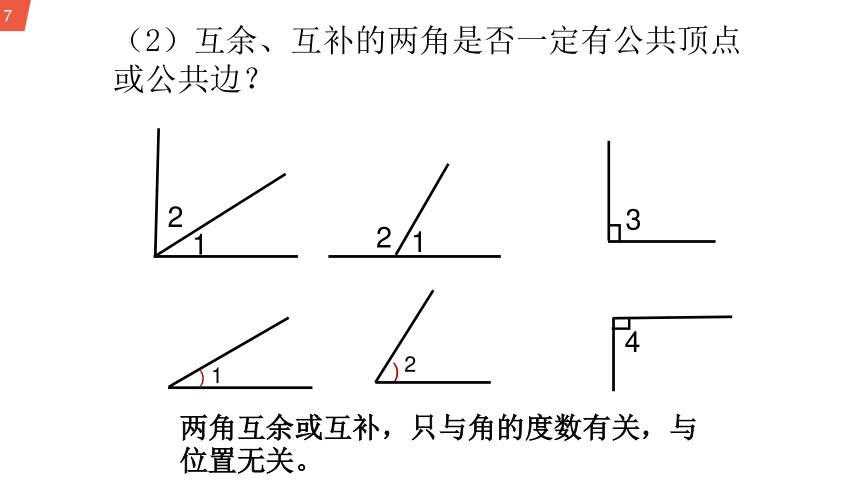
(2)互余、互补的两角是否一定有公共顶点或公共边?
1
2
1
2
)
1
)
2
┐
3
┐
4
两角互余或互补,只与角的度数有关,与位置无关。
(3)∠1 + ∠2 + ∠3 = 90°(180°),能说∠1 、∠2、 ∠3 互余(互补)吗?
不能,互余或互补是两个角之间的数量关系。
1
2
3
1
2
3
即学即练
2、已知∠1与∠2互补,∠1=40°,∠2= 。
3、(必考题)已知∠A=115°,∠B是∠A的补角,则∠B的余角
为 °
4、已知∠A和∠B互余,那么这两个角的补角之和为( )
A.90° B.180° C.270° D.360°
140°
25
C
任务二、余角、补角的性质
(一)余角的性质
如图,∠AOC=∠AOD=90°,找出∠3的两个余角,它们相等吗?为什么?与同学交流。
1
3
2
A
B
C
D
解:∠3的余角为∠1,∠2。∠1=∠2
∵∠1+∠3=90°
∠2+∠3=90°
∴∠1=90°-∠3
∠2=90°-∠3
∴∠1=∠2
结论:同角的余角相等。
几何语言:∵∠1+∠3=90°
∠2+∠3=90°
∴∠1=∠2
O
(一)余角的性质
如图,∠AOC=∠COE=90°,且∠1=∠3,那么它们的余角相等吗?为什么?
解:相等
∵∠1+∠2=90°,∠3+∠4=90°
∴∠2=90°-∠1
∠4=90°-∠3
∵∠1=∠3
∴∠2=∠4
结论:等角的余角相等。
几何语言:∵∠1+∠2=90°
∠3+∠4=90°
且∠1=∠3
∴∠2=∠4
1
2
3
4
A
B
C
D
E
O
余角的性质:同角或等角的余角相等。
如图,直线AB,CD相交于点O,找出∠4的两个补角,它们相等吗?为什么?与同学交流。
解:∠4的补角为∠1,∠3。∠1=∠3
∵∠1+∠4=180°
∠3+∠4=180°
∴∠1=180°-∠4
∠3=180°-∠4
∴∠1=∠3
结论:同角的补角相等。
几何语言:∵∠1+∠4=180°
∠3+∠4=180°
∴∠1=∠3
(二)补角的性质
1
2
3
4
A
B
C
D
O
如图,直线AB,CD相交于点O,∠2=∠4,那么它们的补角相等吗?与同学交流。
解:相等
∵∠1+∠2=180°,∠3+∠4=180°
∴∠1=180°-∠2
∠3=180°-∠4
∵∠2=∠4
∴∠1=∠3
结论:等角的补角相等。
几何语言:∵∠1+∠2=180°
∠3+∠4=180°
且∠2=∠4
∴∠1=∠3
补角的性质:同角或等角的补角相等。
(二)补角的性质
1
2
3
4
A
B
C
D
O
即学即练
2、如图,已知A,O,E三点在同一条直线上,∠1=∠2,且∠1与∠4互余。
(1)∠3与∠2互余吗?为什么?
(2)∠3和∠4有什么关系?
(3)求∠3的补角。
1
2
3
4
即学即练
1、(聊城期中)已知∠1+∠2=180°且∠2=∠3,则∠3+∠1=180°,依据是( )
A.同角的补角相等 B.等角的补角相等
C.等量代换 D.补角的定义
B
典例精讲
例:一个角的补角是它的余角的3倍,求这个角的度数。
解:设这个角是x°,那么它的补角是(180-x)°,余角是(90-x)°,根据题意得:
180-x=3(90-x)
解方程,得 x=45
经检验,x=45符合题意。
所以,这个角是45°.
即学即练
1、(潍坊期中)一个角的余角与这个角的补角之和为130°,求这个角的度数。
2、(聊城期中)已知一个角的补角比它的余角的2倍大45°,求这个角。
巩固应用
1、(甘肃中考)已知∠A=40°,则∠A的余角的大小为 。
2、(菏泽月考)若一个角的补角加上10°等于这个角的余角的3倍,则这个角的度数为 。
3、如果∠1与∠2互余,∠2与∠3互补,那么∠1与∠3的关系是( )
A.∠1=∠3 B.∠1=∠3-90°
C.∠1=∠3+90° D.以上都不对
巩固应用
4、(阳谷期末)如图所示,点C,O,B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,下列结论:①∠EOD=90°;②∠COE=∠AOE;③∠AOE+∠DOC=180°;④互余的角有4对。其中正确的有( )
A.1个 B.2个 C.3个 D.4个
C
E
D
B
O
A
总结归纳
我的收获
1、互余、互补的定义
2、互余互补的计算
3、余角、补角的性质
第6章
基本的几何图形
6.6 余角和补角
1、理解余角和补角的概念,会判断两个角的互余和互补关系。
2、探索并掌握同角或等角的余角相等、同角或等角的补角相等的性质的运算及解决一些实际问题。
学习目标
任务一、互余、互补定义
(一)问题探究
如图所示,你能说出图中∠α与∠β的和以及∠1与∠2的和各是多少?
)
)
α
β
α
β
)
)
1
2
)
)
观察与发现:
(二)定义
如果两个角的和为90°,就说这两个角 互为余角 ,简称互余.其中一个角叫做另一个角的余角.
如果两个角的和为180°,就说这两个角 互为补角,简称互补.其中一个角叫做另一个角的补角.
即学即练
1、在图中找出互余和互补的角
┐
┌
对定义的正确理解:
(1)定义中的“互为”一词如何理解?
如果 1与 2互余,那么 1的余角是 2 ,同样 2的余角是 1 ;如果 1与 2互补,那么 1的补角是 2 , 同样 2的补角是 1。
┐
1
2
1
2
(2)互余、互补的两角是否一定有公共顶点或公共边?
1
2
1
2
)
1
)
2
┐
3
┐
4
两角互余或互补,只与角的度数有关,与位置无关。
(3)∠1 + ∠2 + ∠3 = 90°(180°),能说∠1 、∠2、 ∠3 互余(互补)吗?
不能,互余或互补是两个角之间的数量关系。
1
2
3
1
2
3
即学即练
2、已知∠1与∠2互补,∠1=40°,∠2= 。
3、(必考题)已知∠A=115°,∠B是∠A的补角,则∠B的余角
为 °
4、已知∠A和∠B互余,那么这两个角的补角之和为( )
A.90° B.180° C.270° D.360°
140°
25
C
任务二、余角、补角的性质
(一)余角的性质
如图,∠AOC=∠AOD=90°,找出∠3的两个余角,它们相等吗?为什么?与同学交流。
1
3
2
A
B
C
D
解:∠3的余角为∠1,∠2。∠1=∠2
∵∠1+∠3=90°
∠2+∠3=90°
∴∠1=90°-∠3
∠2=90°-∠3
∴∠1=∠2
结论:同角的余角相等。
几何语言:∵∠1+∠3=90°
∠2+∠3=90°
∴∠1=∠2
O
(一)余角的性质
如图,∠AOC=∠COE=90°,且∠1=∠3,那么它们的余角相等吗?为什么?
解:相等
∵∠1+∠2=90°,∠3+∠4=90°
∴∠2=90°-∠1
∠4=90°-∠3
∵∠1=∠3
∴∠2=∠4
结论:等角的余角相等。
几何语言:∵∠1+∠2=90°
∠3+∠4=90°
且∠1=∠3
∴∠2=∠4
1
2
3
4
A
B
C
D
E
O
余角的性质:同角或等角的余角相等。
如图,直线AB,CD相交于点O,找出∠4的两个补角,它们相等吗?为什么?与同学交流。
解:∠4的补角为∠1,∠3。∠1=∠3
∵∠1+∠4=180°
∠3+∠4=180°
∴∠1=180°-∠4
∠3=180°-∠4
∴∠1=∠3
结论:同角的补角相等。
几何语言:∵∠1+∠4=180°
∠3+∠4=180°
∴∠1=∠3
(二)补角的性质
1
2
3
4
A
B
C
D
O
如图,直线AB,CD相交于点O,∠2=∠4,那么它们的补角相等吗?与同学交流。
解:相等
∵∠1+∠2=180°,∠3+∠4=180°
∴∠1=180°-∠2
∠3=180°-∠4
∵∠2=∠4
∴∠1=∠3
结论:等角的补角相等。
几何语言:∵∠1+∠2=180°
∠3+∠4=180°
且∠2=∠4
∴∠1=∠3
补角的性质:同角或等角的补角相等。
(二)补角的性质
1
2
3
4
A
B
C
D
O
即学即练
2、如图,已知A,O,E三点在同一条直线上,∠1=∠2,且∠1与∠4互余。
(1)∠3与∠2互余吗?为什么?
(2)∠3和∠4有什么关系?
(3)求∠3的补角。
1
2
3
4
即学即练
1、(聊城期中)已知∠1+∠2=180°且∠2=∠3,则∠3+∠1=180°,依据是( )
A.同角的补角相等 B.等角的补角相等
C.等量代换 D.补角的定义
B
典例精讲
例:一个角的补角是它的余角的3倍,求这个角的度数。
解:设这个角是x°,那么它的补角是(180-x)°,余角是(90-x)°,根据题意得:
180-x=3(90-x)
解方程,得 x=45
经检验,x=45符合题意。
所以,这个角是45°.
即学即练
1、(潍坊期中)一个角的余角与这个角的补角之和为130°,求这个角的度数。
2、(聊城期中)已知一个角的补角比它的余角的2倍大45°,求这个角。
巩固应用
1、(甘肃中考)已知∠A=40°,则∠A的余角的大小为 。
2、(菏泽月考)若一个角的补角加上10°等于这个角的余角的3倍,则这个角的度数为 。
3、如果∠1与∠2互余,∠2与∠3互补,那么∠1与∠3的关系是( )
A.∠1=∠3 B.∠1=∠3-90°
C.∠1=∠3+90° D.以上都不对
巩固应用
4、(阳谷期末)如图所示,点C,O,B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,下列结论:①∠EOD=90°;②∠COE=∠AOE;③∠AOE+∠DOC=180°;④互余的角有4对。其中正确的有( )
A.1个 B.2个 C.3个 D.4个
C
E
D
B
O
A
总结归纳
我的收获
1、互余、互补的定义
2、互余互补的计算
3、余角、补角的性质
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
