29.2 三视图 分层练习(含答案)2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 29.2 三视图 分层练习(含答案)2024-2025学年数学人教版九年级下册 | 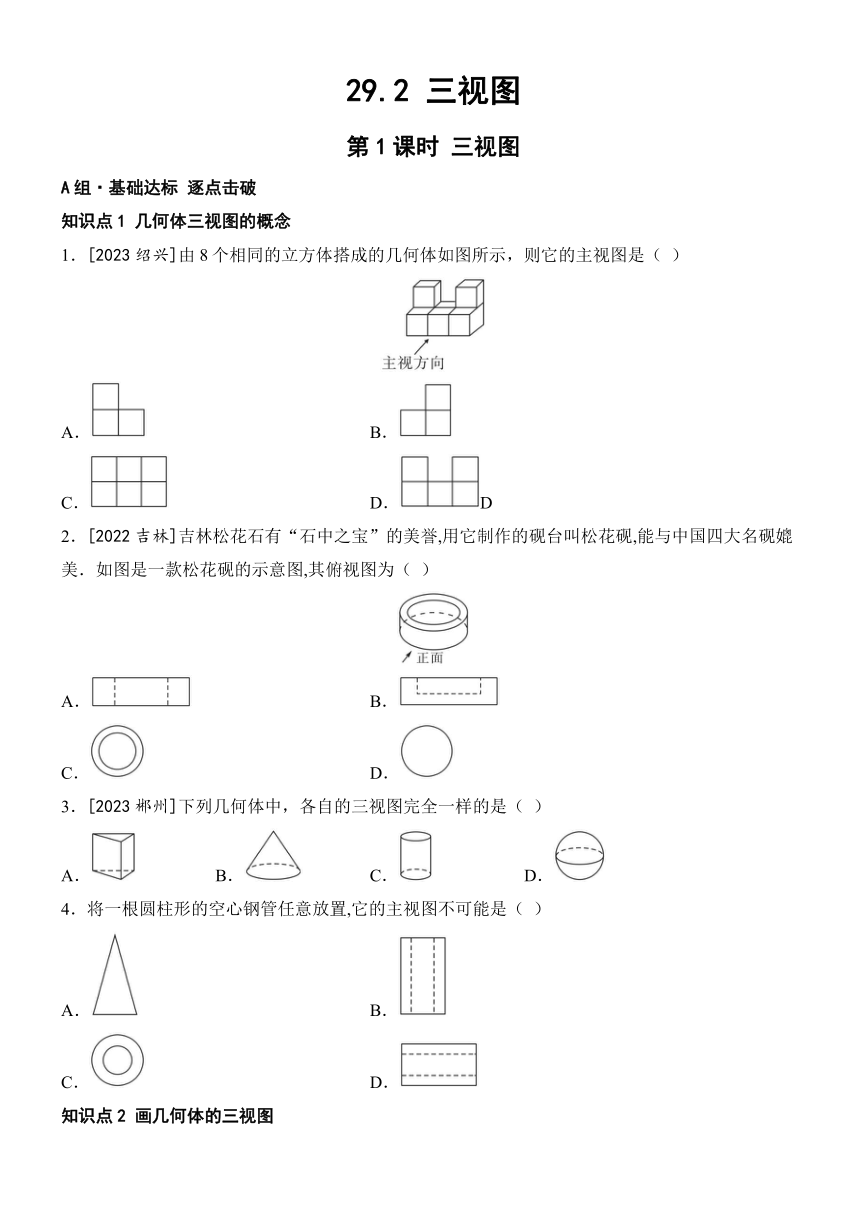 | |
| 格式 | docx | ||
| 文件大小 | 336.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-02 21:29:44 | ||
图片预览


文档简介
29.2 三视图
第1课时 三视图
A组·基础达标 逐点击破
知识点1 几何体三视图的概念
1.[2023绍兴]由8个相同的立方体搭成的几何体如图所示,则它的主视图是( )
A. B.
C. D.D
2.[2022吉林]吉林松花石有“石中之宝”的美誉,用它制作的砚台叫松花砚,能与中国四大名砚媲美.如图是一款松花砚的示意图,其俯视图为( )
A. B.
C. D.
3.[2023郴州]下列几何体中,各自的三视图完全一样的是( )
A. B. C. D.
4.将一根圆柱形的空心钢管任意放置,它的主视图不可能是( )
A. B.
C. D.
知识点2 画几何体的三视图
5.如图是一个蘑菇形小零件,其上部是一个半球体,下部是一个圆柱体,作出它的三视图.
B组·能力提升 强化突破
6.[2023金华]某物体如图所示,其俯视图是( )
A. B.
C. D.
7.[2022江西]如图是由四个完全相同的小正方体搭成的几何体,它的俯视图为( )
A. B. C. D.
C组·核心素养拓展 素养渗透
8.【数学建模】图②是图①中长方体的三视图,用表示面积,,,则( )
A. B.
C. D.
第2课时 由三视图描述物体的形状
A组·基础达标 逐点击破
知识点 由三视图想象出实物原型
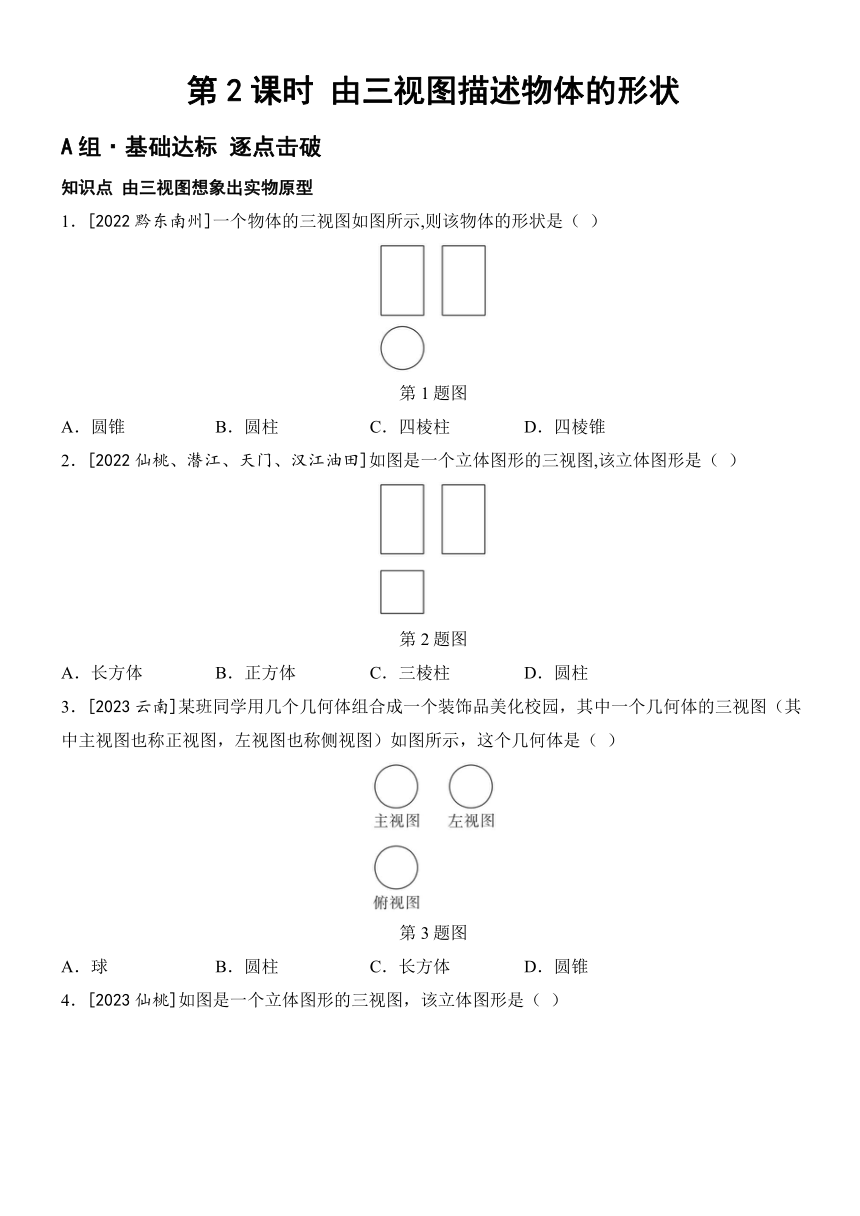
1.[2022黔东南州]一个物体的三视图如图所示,则该物体的形状是( )
第1题图
A.圆锥 B.圆柱 C.四棱柱 D.四棱锥
2.[2022仙桃、潜江、天门、汉江油田]如图是一个立体图形的三视图,该立体图形是( )
第2题图
A.长方体 B.正方体 C.三棱柱 D.圆柱
3.[2023云南]某班同学用几个几何体组合成一个装饰品美化校园,其中一个几何体的三视图(其中主视图也称正视图,左视图也称侧视图)如图所示,这个几何体是( )
第3题图
A.球 B.圆柱 C.长方体 D.圆锥
4.[2023仙桃]如图是一个立体图形的三视图,该立体图形是( )
第4题图
A.三棱柱 B.圆柱 C.三棱锥 D.圆锥
B组·能力提升 强化突破
5.[2023广元]某几何体是由四个大小相同的小立方块拼成,其俯视图如图所示,图中数字表示该位置上的小立方块个数,则这个几何体的左视图是( )
A. B. C. D.
6.[2023眉山]由相同的小正方体搭成的立体图形的部分视图如图所示,则搭成该立体图形的小正方体的最少个数为( )
第6题图
A.6 B.9 C.10 D.14
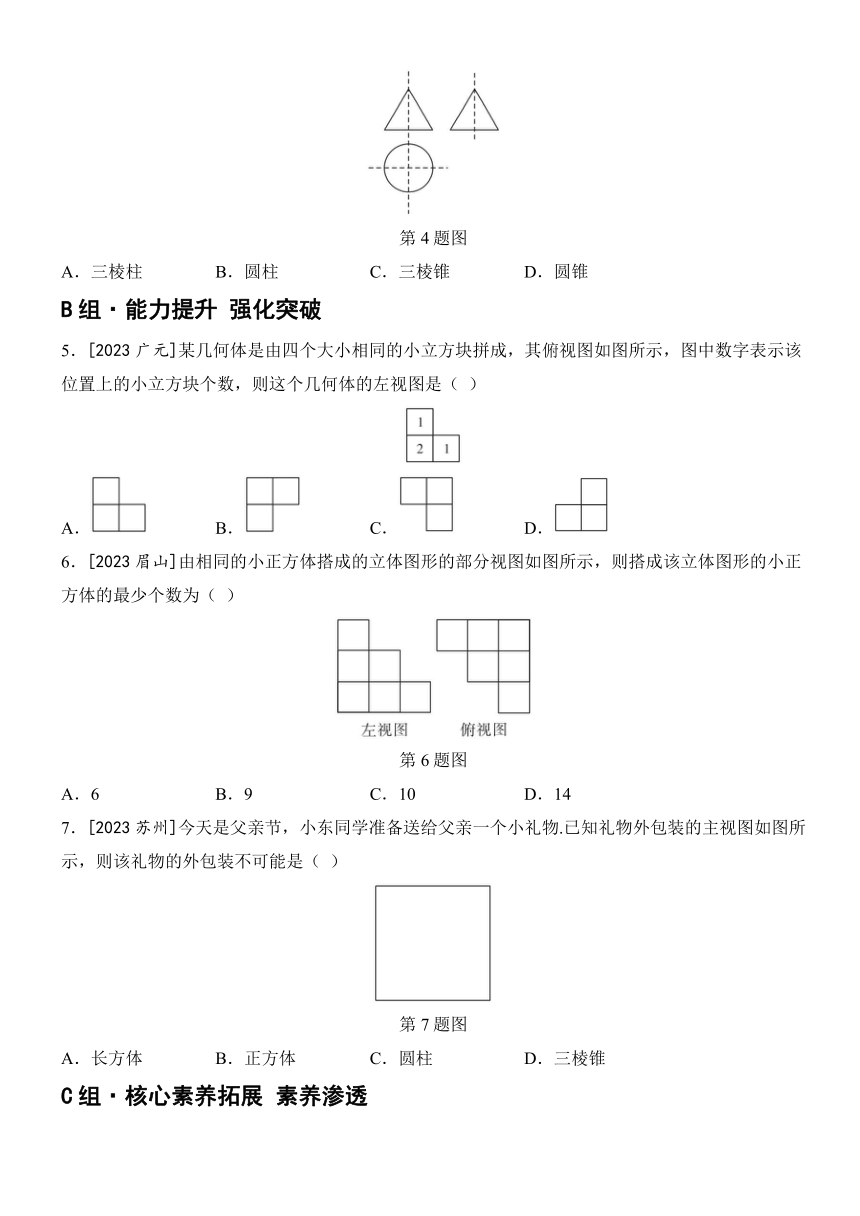
7.[2023苏州]今天是父亲节,小东同学准备送给父亲一个小礼物.已知礼物外包装的主视图如图所示,则该礼物的外包装不可能是( )
第7题图
A.长方体 B.正方体 C.圆柱 D.三棱锥
C组·核心素养拓展 素养渗透
8.【空间观念】我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称为“堑堵”.已知“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的体积为( )
A. B. C. D.16
第3课时 由三视图到表面展开图
A组·基础达标 逐点击破
知识点 由三视图求物体的表面积
1.下列几何体中,其侧面展开图为扇形的是( )
A. B.
C. D.
2.一个几何体的三视图如图所示,则这个几何体的表面积是( )
A. B. C. D.
3.[2023益阳模拟]如图是某圆锥的主视图和左视图,该圆锥的侧面积是( )
A. B. C. D.
4.[2023衡阳模拟]一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为,则的值为( )
A. B. C. D.2
5.如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是________.
6.如图是某几何体的展开图.
(1) 这个几何体的名称是____;
(2) 画出这个几何体的三视图;
(3) 求这个几何体的体积 取.
7.如图是一个几何体的三视图.
(1) 这个几何体的名称是____;
(2) 依据图中给出的数据,计算出这个几何体的侧面积.
B组·能力提升 强化突破
8.[2022河北]某款“不倒翁”(图①)的主视图是图②,,分别与所在圆相切于点,.若该圆的半径是, ,则的长是( )
A. B. C. D.
9.[2023济宁]一个几何体的三视图如图所示,则这个几何体的表面积是( )
A. B. C. D.
10.一个几何体的三视图如图所示,则该几何体的表面积为__________.
第10题图
11.一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
第11题图
C组·核心素养拓展 素养渗透
12.[2022铁岭模拟]【创新意识,空间观念】如图①是一个直四棱柱,如图②是它的三视图,其俯视图是等腰梯形.
(1) 根据图②中给出的数据,可得俯视图(等腰梯形)的高为____,腰长为________;
(2) 主视图和左视图中________,________,________,____;
(3) 求这个直四棱柱的侧面积.
29.2 三视图
第1课时 三视图
A组·基础达标 逐点击破
知识点1 几何体三视图的概念
1.D 2.C 3.D 4.A
知识点2 画几何体的三视图
5.解:如答图.
第5题答图
B组·能力提升 强化突破
6.B 7.A
C组·核心素养拓展 素养渗透
8.C
第2课时 由三视图描述物体的形状
A组·基础达标 逐点击破
知识点 由三视图想象出实物原型
1.B 2.A 3.A 4.D
B组·能力提升 强化突破
5.D 6.B 7.D
C组·核心素养拓展 素养渗透
8.D
第3课时 由三视图到表面展开图
A组·基础达标 逐点击破
知识点 由三视图求物体的表面积
1.C 2.D 3.C 4.A
5.
6.(1) 圆柱
(2) 解:如答图.
第6题答图
(3) 体积为.
7.(1) 圆锥
(2) 解:.
B组·能力提升 强化突破
8.A 9.B
10.
11.解:该几何体的形状是直四棱柱.由三视图知,棱柱底面菱形的对角线长分别为,, 菱形的边长为,棱柱的侧面积为
C组·核心素养拓展 素养渗透
12.(1) 6;
[解析]如答图,过点作于点.
第12题答图
则.
,
,
,
.
高为6,腰长为.
(2) ; ; ; 6
(3) 解:
.
故这个直四棱柱的侧面积是.
第1课时 三视图
A组·基础达标 逐点击破
知识点1 几何体三视图的概念
1.[2023绍兴]由8个相同的立方体搭成的几何体如图所示,则它的主视图是( )
A. B.
C. D.D
2.[2022吉林]吉林松花石有“石中之宝”的美誉,用它制作的砚台叫松花砚,能与中国四大名砚媲美.如图是一款松花砚的示意图,其俯视图为( )
A. B.
C. D.
3.[2023郴州]下列几何体中,各自的三视图完全一样的是( )
A. B. C. D.
4.将一根圆柱形的空心钢管任意放置,它的主视图不可能是( )
A. B.
C. D.
知识点2 画几何体的三视图
5.如图是一个蘑菇形小零件,其上部是一个半球体,下部是一个圆柱体,作出它的三视图.
B组·能力提升 强化突破
6.[2023金华]某物体如图所示,其俯视图是( )
A. B.
C. D.
7.[2022江西]如图是由四个完全相同的小正方体搭成的几何体,它的俯视图为( )
A. B. C. D.
C组·核心素养拓展 素养渗透
8.【数学建模】图②是图①中长方体的三视图,用表示面积,,,则( )
A. B.
C. D.
第2课时 由三视图描述物体的形状
A组·基础达标 逐点击破
知识点 由三视图想象出实物原型
1.[2022黔东南州]一个物体的三视图如图所示,则该物体的形状是( )
第1题图
A.圆锥 B.圆柱 C.四棱柱 D.四棱锥
2.[2022仙桃、潜江、天门、汉江油田]如图是一个立体图形的三视图,该立体图形是( )
第2题图
A.长方体 B.正方体 C.三棱柱 D.圆柱
3.[2023云南]某班同学用几个几何体组合成一个装饰品美化校园,其中一个几何体的三视图(其中主视图也称正视图,左视图也称侧视图)如图所示,这个几何体是( )
第3题图
A.球 B.圆柱 C.长方体 D.圆锥
4.[2023仙桃]如图是一个立体图形的三视图,该立体图形是( )
第4题图
A.三棱柱 B.圆柱 C.三棱锥 D.圆锥
B组·能力提升 强化突破
5.[2023广元]某几何体是由四个大小相同的小立方块拼成,其俯视图如图所示,图中数字表示该位置上的小立方块个数,则这个几何体的左视图是( )
A. B. C. D.
6.[2023眉山]由相同的小正方体搭成的立体图形的部分视图如图所示,则搭成该立体图形的小正方体的最少个数为( )
第6题图
A.6 B.9 C.10 D.14
7.[2023苏州]今天是父亲节,小东同学准备送给父亲一个小礼物.已知礼物外包装的主视图如图所示,则该礼物的外包装不可能是( )
第7题图
A.长方体 B.正方体 C.圆柱 D.三棱锥
C组·核心素养拓展 素养渗透
8.【空间观念】我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称为“堑堵”.已知“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的体积为( )
A. B. C. D.16
第3课时 由三视图到表面展开图
A组·基础达标 逐点击破
知识点 由三视图求物体的表面积
1.下列几何体中,其侧面展开图为扇形的是( )
A. B.
C. D.
2.一个几何体的三视图如图所示,则这个几何体的表面积是( )
A. B. C. D.
3.[2023益阳模拟]如图是某圆锥的主视图和左视图,该圆锥的侧面积是( )
A. B. C. D.
4.[2023衡阳模拟]一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为,则的值为( )
A. B. C. D.2
5.如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是________.
6.如图是某几何体的展开图.
(1) 这个几何体的名称是____;
(2) 画出这个几何体的三视图;
(3) 求这个几何体的体积 取.
7.如图是一个几何体的三视图.
(1) 这个几何体的名称是____;
(2) 依据图中给出的数据,计算出这个几何体的侧面积.
B组·能力提升 强化突破
8.[2022河北]某款“不倒翁”(图①)的主视图是图②,,分别与所在圆相切于点,.若该圆的半径是, ,则的长是( )
A. B. C. D.
9.[2023济宁]一个几何体的三视图如图所示,则这个几何体的表面积是( )
A. B. C. D.
10.一个几何体的三视图如图所示,则该几何体的表面积为__________.
第10题图
11.一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
第11题图
C组·核心素养拓展 素养渗透
12.[2022铁岭模拟]【创新意识,空间观念】如图①是一个直四棱柱,如图②是它的三视图,其俯视图是等腰梯形.
(1) 根据图②中给出的数据,可得俯视图(等腰梯形)的高为____,腰长为________;
(2) 主视图和左视图中________,________,________,____;
(3) 求这个直四棱柱的侧面积.
29.2 三视图
第1课时 三视图
A组·基础达标 逐点击破
知识点1 几何体三视图的概念
1.D 2.C 3.D 4.A
知识点2 画几何体的三视图
5.解:如答图.
第5题答图
B组·能力提升 强化突破
6.B 7.A
C组·核心素养拓展 素养渗透
8.C
第2课时 由三视图描述物体的形状
A组·基础达标 逐点击破
知识点 由三视图想象出实物原型
1.B 2.A 3.A 4.D
B组·能力提升 强化突破
5.D 6.B 7.D
C组·核心素养拓展 素养渗透
8.D
第3课时 由三视图到表面展开图
A组·基础达标 逐点击破
知识点 由三视图求物体的表面积
1.C 2.D 3.C 4.A
5.
6.(1) 圆柱
(2) 解:如答图.
第6题答图
(3) 体积为.
7.(1) 圆锥
(2) 解:.
B组·能力提升 强化突破
8.A 9.B
10.
11.解:该几何体的形状是直四棱柱.由三视图知,棱柱底面菱形的对角线长分别为,, 菱形的边长为,棱柱的侧面积为
C组·核心素养拓展 素养渗透
12.(1) 6;
[解析]如答图,过点作于点.
第12题答图
则.
,
,
,
.
高为6,腰长为.
(2) ; ; ; 6
(3) 解:
.
故这个直四棱柱的侧面积是.
