29.3 课题学习 制作立体模型 分层练习(含答案) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 29.3 课题学习 制作立体模型 分层练习(含答案) 2024-2025学年数学人教版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 176.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-02 21:29:36 | ||
图片预览

文档简介
29.3 课题学习 制作立体模型
A组·基础达标 逐点击破
知识点 由平面展开图制作立体图形
1.[2022宿迁]下列展开图中,是正方体展开图的是( )
A. B.
C. D.
2.[2022泰州]如图为一个几何体的展开图,则该几何体是( )
A.三棱锥 B.四棱锥 C.四棱柱 D.圆锥
3.如图是一个多面体的表面展开图,每个面都标注了序号.若多面体的底面是面③,则多面体的上面是( )
A.面① B.面② C.面⑤ D.面⑥
4.[2023达州]下列图形中,是长方体展开图的是( )
A. B.
C. D.
5.如图所示的正方体的展开图为( )
A. B.
C. D.
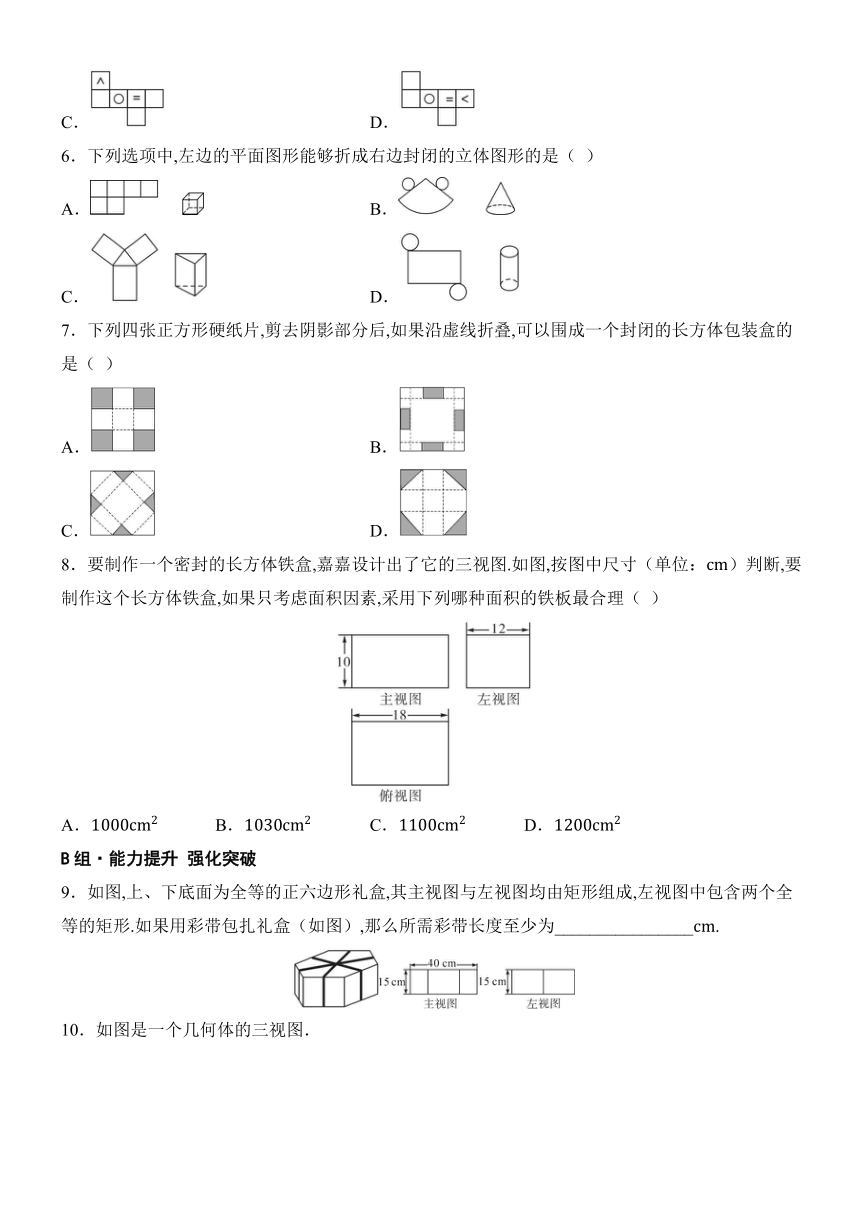
6.下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )
A. B.
C. D.
7.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )
A. B.
C. D.
8.要制作一个密封的长方体铁盒,嘉嘉设计出了它的三视图.如图,按图中尺寸(单位:)判断,要制作这个长方体铁盒,如果只考虑面积因素,采用下列哪种面积的铁板最合理( )
A. B. C. D.
B组·能力提升 强化突破
9.如图,上、下底面为全等的正六边形礼盒,其主视图与左视图均由矩形组成,左视图中包含两个全等的矩形.如果用彩带包扎礼盒(如图),那么所需彩带长度至少为________________.
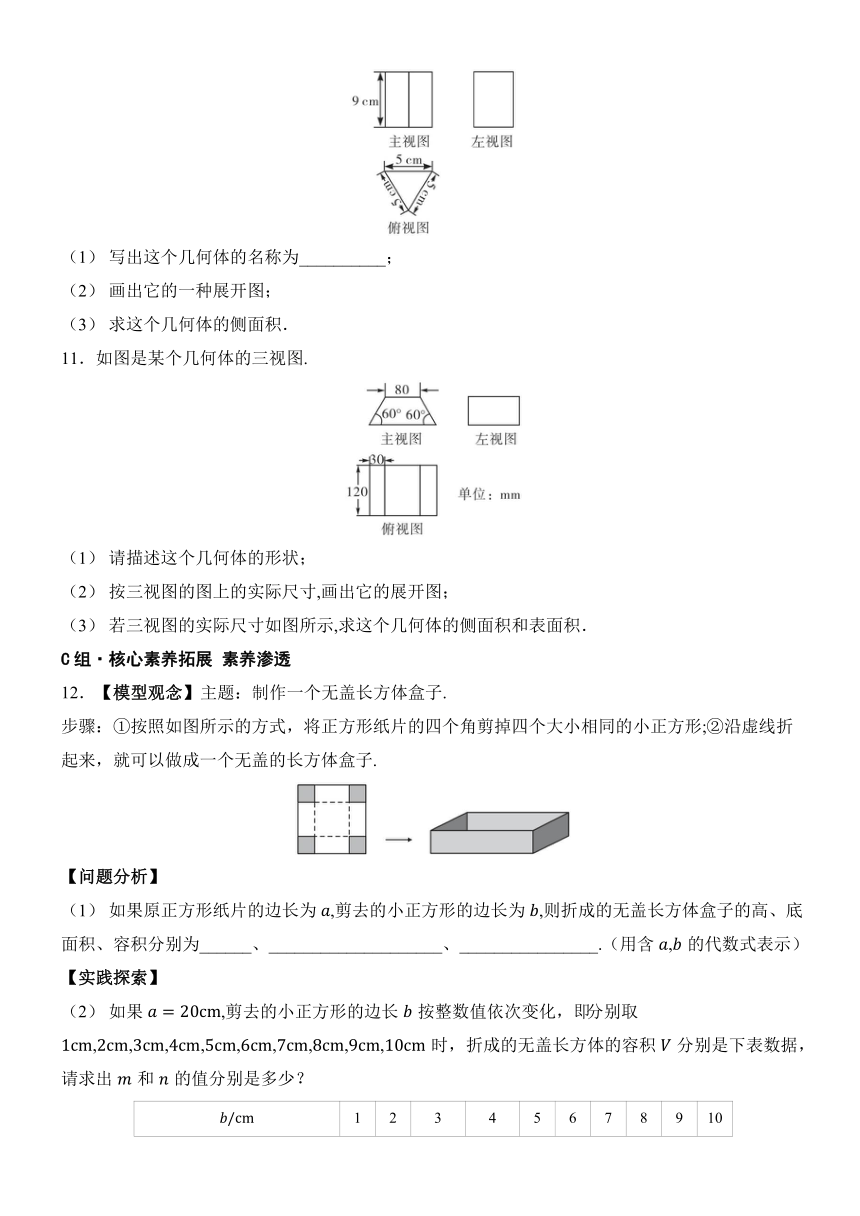
10.如图是一个几何体的三视图.
(1) 写出这个几何体的名称为__________;
(2) 画出它的一种展开图;
(3) 求这个几何体的侧面积.
11.如图是某个几何体的三视图.
(1) 请描述这个几何体的形状;
(2) 按三视图的图上的实际尺寸,画出它的展开图;
(3) 若三视图的实际尺寸如图所示,求这个几何体的侧面积和表面积.
C组·核心素养拓展 素养渗透
12.【模型观念】主题:制作一个无盖长方体盒子.
步骤:①按照如图所示的方式,将正方形纸片的四个角剪掉四个大小相同的小正方形;②沿虚线折起来,就可以做成一个无盖的长方体盒子.
【问题分析】
(1) 如果原正方形纸片的边长为,剪去的小正方形的边长为,则折成的无盖长方体盒子的高、底面积、容积分别为______、____________________、________________.(用含,的代数式表示)
【实践探索】
(2) 如果,剪去的小正方形的边长按整数值依次变化,即分别取,,,,,,,,,时,折成的无盖长方体的容积分别是下表数据,请求出和的值分别是多少?
1 2 3 4 5 6 7 8 9 10
324 512 500 384 252 128 36 0
【实践分析】
观察绘制的统计表,你发现,随着减去的小正方形的边长的增大,所折无盖长方体盒子的容积如何变化?并分析猜想当剪去图形的边长为多少时,所得的无盖长方体的容积最大,此时最大容积是多少?
29.3 课题学习 制作立体模型
A组·基础达标 逐点击破
知识点 由平面展开图制作立体图形
1.C 2.B 3.C 4.C 5.A 6.D 7.C 8.C
B组·能力提升 强化突破
9.
10.(1) 正三棱柱
(2) 解:展开图如答图(答案不唯一).
第10题答图
(3) .
答:这个几何体的侧面积是.
11.(1) 解:底面是上底为,下底为,高为的等腰梯形,棱长为的直四棱柱.
(2) 如答图.
第11题答图
(3) .
C组·核心素养拓展 素养渗透
12.(1) ; ;
(2) 解:当,时,,即;
当,时,,即.
(3) 由表中数据可知,随着减去的小正方形的边长的增大,所折无盖长方体盒子的容积先增大后减小;
由表中数据可知,当时,容积最大为.
A组·基础达标 逐点击破
知识点 由平面展开图制作立体图形
1.[2022宿迁]下列展开图中,是正方体展开图的是( )
A. B.
C. D.
2.[2022泰州]如图为一个几何体的展开图,则该几何体是( )
A.三棱锥 B.四棱锥 C.四棱柱 D.圆锥
3.如图是一个多面体的表面展开图,每个面都标注了序号.若多面体的底面是面③,则多面体的上面是( )
A.面① B.面② C.面⑤ D.面⑥
4.[2023达州]下列图形中,是长方体展开图的是( )
A. B.
C. D.
5.如图所示的正方体的展开图为( )
A. B.
C. D.
6.下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )
A. B.
C. D.
7.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )
A. B.
C. D.
8.要制作一个密封的长方体铁盒,嘉嘉设计出了它的三视图.如图,按图中尺寸(单位:)判断,要制作这个长方体铁盒,如果只考虑面积因素,采用下列哪种面积的铁板最合理( )
A. B. C. D.
B组·能力提升 强化突破
9.如图,上、下底面为全等的正六边形礼盒,其主视图与左视图均由矩形组成,左视图中包含两个全等的矩形.如果用彩带包扎礼盒(如图),那么所需彩带长度至少为________________.
10.如图是一个几何体的三视图.
(1) 写出这个几何体的名称为__________;
(2) 画出它的一种展开图;
(3) 求这个几何体的侧面积.
11.如图是某个几何体的三视图.
(1) 请描述这个几何体的形状;
(2) 按三视图的图上的实际尺寸,画出它的展开图;
(3) 若三视图的实际尺寸如图所示,求这个几何体的侧面积和表面积.
C组·核心素养拓展 素养渗透
12.【模型观念】主题:制作一个无盖长方体盒子.
步骤:①按照如图所示的方式,将正方形纸片的四个角剪掉四个大小相同的小正方形;②沿虚线折起来,就可以做成一个无盖的长方体盒子.
【问题分析】
(1) 如果原正方形纸片的边长为,剪去的小正方形的边长为,则折成的无盖长方体盒子的高、底面积、容积分别为______、____________________、________________.(用含,的代数式表示)
【实践探索】
(2) 如果,剪去的小正方形的边长按整数值依次变化,即分别取,,,,,,,,,时,折成的无盖长方体的容积分别是下表数据,请求出和的值分别是多少?
1 2 3 4 5 6 7 8 9 10
324 512 500 384 252 128 36 0
【实践分析】
观察绘制的统计表,你发现,随着减去的小正方形的边长的增大,所折无盖长方体盒子的容积如何变化?并分析猜想当剪去图形的边长为多少时,所得的无盖长方体的容积最大,此时最大容积是多少?
29.3 课题学习 制作立体模型
A组·基础达标 逐点击破
知识点 由平面展开图制作立体图形
1.C 2.B 3.C 4.C 5.A 6.D 7.C 8.C
B组·能力提升 强化突破
9.
10.(1) 正三棱柱
(2) 解:展开图如答图(答案不唯一).
第10题答图
(3) .
答:这个几何体的侧面积是.
11.(1) 解:底面是上底为,下底为,高为的等腰梯形,棱长为的直四棱柱.
(2) 如答图.
第11题答图
(3) .
C组·核心素养拓展 素养渗透
12.(1) ; ;
(2) 解:当,时,,即;
当,时,,即.
(3) 由表中数据可知,随着减去的小正方形的边长的增大,所折无盖长方体盒子的容积先增大后减小;
由表中数据可知,当时,容积最大为.
