第二十八章 锐角三角函数 单元复习课(含答案) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 第二十八章 锐角三角函数 单元复习课(含答案) 2024-2025学年数学人教版九年级下册 | 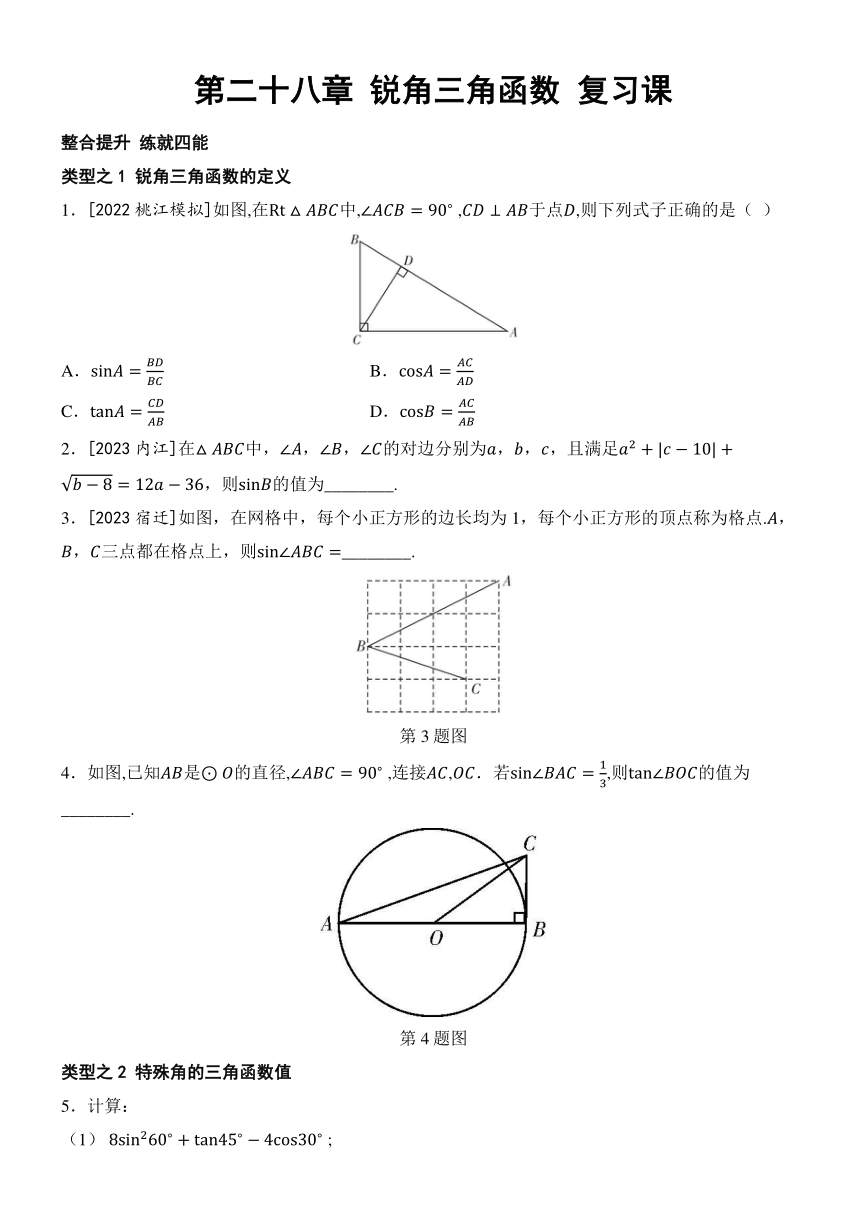 | |
| 格式 | docx | ||
| 文件大小 | 280.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-02 21:38:43 | ||
图片预览




文档简介
第二十八章 锐角三角函数 复习课
整合提升 练就四能
类型之1 锐角三角函数的定义
1.[2022桃江模拟]如图,在中, ,于点,则下列式子正确的是( )
A. B.
C. D.
2.[2023内江]在中,,,的对边分别为,,,且满足,则的值为________.
3.[2023宿迁]如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.,,三点都在格点上,则________.
第3题图
4.如图,已知是的直径, ,连接,.若,则的值为 ________.
第4题图
类型之2 特殊角的三角函数值
5.计算:
(1) ;
(2) .
类型之3 解直角三角形
6.如图,点,,在每个正方形边长为1的网格的格点上,则( )
A. B. C. D.
7.根据下列条件,解直角三角形.
(1) 在中, ,,;
(2) 在中, , ,
8.如图,在中, ,,,点在上,且.
(1) 的长为____;
(2) 求的值.
类型之4 解直角三角形的应用
9.如图,在由四个全等的直角三角形和中间一个小正方形拼成的大正方形中,,连接.设 , .若正方形与正方形的面积之比为, ,则( )
第9题图
A.5 B.4 C.3 D.2
10.某海域有,两个航标,航标在航标北偏西 方向上,距航标.有一艘巡航船从航标出发,沿东北方向行驶一段距离后,到达位于航标南偏东 方向的航标处.
第10题图
(1) __ ,__ ;
(2) 该船与航标之间的距离为______________.
11.[2023邵阳模拟]如图,四边形是某水库大坝的横截面示意图,坝高,背水坡的坡角为 .现需要对大坝进行加固,使上底加宽,且加固后背水坡的坡度.求加固后坝底增加的宽度的长.
12.[2023嘉兴、舟山]图①是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图②,摄像头的仰角、俯角均为 ,摄像头的高度,识别的最远水平距离.
(1) 身高的小杜,头部高度为,他站在离摄像头水平距离的点处,请问小杜最少需要下蹲多少厘米才能被识别?
(2) 身高的小若,头部高度为,踮起脚尖可以增高,但仍无法被识别,社区及时将摄像头的仰角、俯角都调整为 (如图③),此时小若能被识别吗?请计算说明.
(结果精确到.参考数据:,,,,,)
类型之5 解直角三角形与圆的结合
13.[2023长沙模拟]如图,在中,,以为直径的分别交,边于点,,过点作于点.
(1) 求证:是的切线;
(2) 若,且,求的半径及的长.
类型之6 数学活动
14.某综合实践研究小组为了测量观察目标时的仰角和俯角,利用量角器和铅锤自制了一个简易测角仪,如图①所示.
(1) 如图②,在点观察所测物体最高点,当量角器零刻度线上,两点均在视线上时,测得视线与铅垂线所夹的锐角为 ,设仰角为 ,用含 的代数式表示 为______________.
(2) 如图③,为了测量广场上空气球离地面的高度,该小组利用自制简易测角仪在点,处分别测得气球的仰角为 ,为 ,地面上点,,在同一水平直线上,,求气球离地面的高度.(参考数据:,,)
素养专练 培养三会
15.【几何直观】如图,的顶点在边长均相同的正方形网格的格点上,则的值为( )
第15题图
A. B. C.2 D.
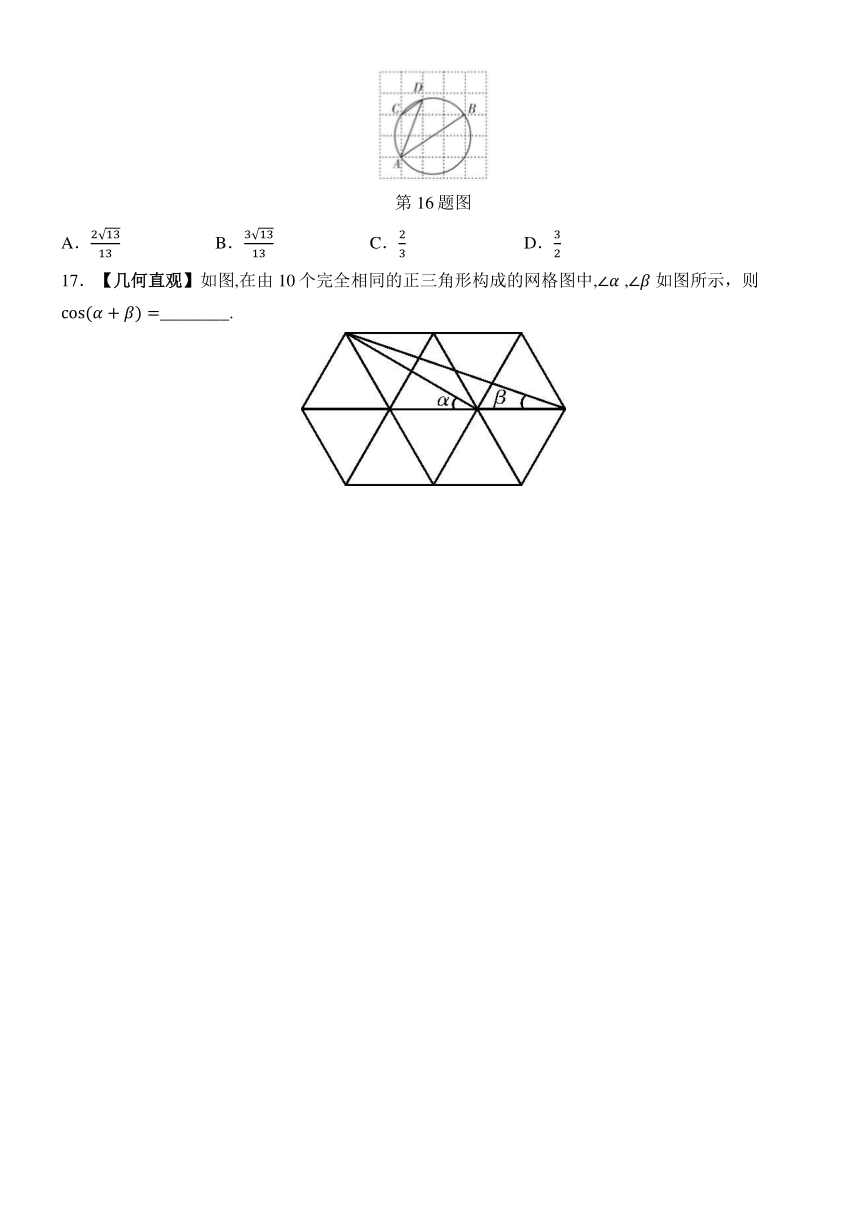
16.【几何直观】如图,在由边长为1的小正方形构成的网格中,点,,都在格点上,以为直径的圆经过点,,则的值为( )
第16题图
A. B. C. D.
17.【几何直观】如图,在由10个完全相同的正三角形构成的网格图中, , 如图所示,则________.
本章复习课
整合提升 练就四能
类型之1 锐角三角函数的定义
1.A
2.
3.
4.
类型之2 特殊角的三角函数值
5.(1) 解:原式.
(2) 原式.
类型之3 解直角三角形
6.B
7.(1) 解: ,,,
.
, .
.
(2) , .
.
,即,
.
8.(1) 4
(2) 解:设,则.
在中,,
即,解得,
,,
.
类型之4 解直角三角形的应用
9.C
10.(1) 45; 60
(2)
11.解:如答图,分别过点,作,交于点,.
第11题答图
四边形是梯形,且,
,,
四边形是矩形,
,.
在中, ,
.
在中,,
,
.
答:加固后坝底增加的宽度的长是.
12.(1) 解:如答图①,过点作的垂线分别交仰角、俯角线于点,,交水平线于点.
第12题答图①
在中, ,
.
,, ,
,
,
,
小杜最少需要下蹲才能被识别.
(2) 如答图②,过点作的垂线分别交仰角、俯角线于点,,交水平线于点.
第12题答图②
在中, ,
.
,, ,,
,
,
小若踮起脚尖后头顶的高度为,
小若头顶超出点的高度为,
踮起脚尖小若能被识别.
类型之5 解直角三角形与圆的结合
13.(1) 证明:如答图①,连接.
第13题答图①
,.
,,
,.
,.
又为的半径,
是的切线.
(2) 解:如答图②,连接,.
为的直径,
,即.
,,
.
在中,,
设,则,
,
,
解得(负值已舍去),
,
的半径为.
四边形是的内接四边形,
.
又,
,
,,,
.
第13题答图②
类型之6 数学活动
14.(1)
(2) 解:设,
, ,
.
,.
在中, ,
,
即,解得,
经检验是方程的解,且符合题意,
.
答:气球离地面的高度约是.
素养专练 培养三会
15.A 16.A
17.
整合提升 练就四能
类型之1 锐角三角函数的定义
1.[2022桃江模拟]如图,在中, ,于点,则下列式子正确的是( )
A. B.
C. D.
2.[2023内江]在中,,,的对边分别为,,,且满足,则的值为________.
3.[2023宿迁]如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.,,三点都在格点上,则________.
第3题图
4.如图,已知是的直径, ,连接,.若,则的值为 ________.
第4题图
类型之2 特殊角的三角函数值
5.计算:
(1) ;
(2) .
类型之3 解直角三角形
6.如图,点,,在每个正方形边长为1的网格的格点上,则( )
A. B. C. D.
7.根据下列条件,解直角三角形.
(1) 在中, ,,;
(2) 在中, , ,
8.如图,在中, ,,,点在上,且.
(1) 的长为____;
(2) 求的值.
类型之4 解直角三角形的应用
9.如图,在由四个全等的直角三角形和中间一个小正方形拼成的大正方形中,,连接.设 , .若正方形与正方形的面积之比为, ,则( )
第9题图
A.5 B.4 C.3 D.2
10.某海域有,两个航标,航标在航标北偏西 方向上,距航标.有一艘巡航船从航标出发,沿东北方向行驶一段距离后,到达位于航标南偏东 方向的航标处.
第10题图
(1) __ ,__ ;
(2) 该船与航标之间的距离为______________.
11.[2023邵阳模拟]如图,四边形是某水库大坝的横截面示意图,坝高,背水坡的坡角为 .现需要对大坝进行加固,使上底加宽,且加固后背水坡的坡度.求加固后坝底增加的宽度的长.
12.[2023嘉兴、舟山]图①是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图②,摄像头的仰角、俯角均为 ,摄像头的高度,识别的最远水平距离.
(1) 身高的小杜,头部高度为,他站在离摄像头水平距离的点处,请问小杜最少需要下蹲多少厘米才能被识别?
(2) 身高的小若,头部高度为,踮起脚尖可以增高,但仍无法被识别,社区及时将摄像头的仰角、俯角都调整为 (如图③),此时小若能被识别吗?请计算说明.
(结果精确到.参考数据:,,,,,)
类型之5 解直角三角形与圆的结合
13.[2023长沙模拟]如图,在中,,以为直径的分别交,边于点,,过点作于点.
(1) 求证:是的切线;
(2) 若,且,求的半径及的长.
类型之6 数学活动
14.某综合实践研究小组为了测量观察目标时的仰角和俯角,利用量角器和铅锤自制了一个简易测角仪,如图①所示.
(1) 如图②,在点观察所测物体最高点,当量角器零刻度线上,两点均在视线上时,测得视线与铅垂线所夹的锐角为 ,设仰角为 ,用含 的代数式表示 为______________.
(2) 如图③,为了测量广场上空气球离地面的高度,该小组利用自制简易测角仪在点,处分别测得气球的仰角为 ,为 ,地面上点,,在同一水平直线上,,求气球离地面的高度.(参考数据:,,)
素养专练 培养三会
15.【几何直观】如图,的顶点在边长均相同的正方形网格的格点上,则的值为( )
第15题图
A. B. C.2 D.
16.【几何直观】如图,在由边长为1的小正方形构成的网格中,点,,都在格点上,以为直径的圆经过点,,则的值为( )
第16题图
A. B. C. D.
17.【几何直观】如图,在由10个完全相同的正三角形构成的网格图中, , 如图所示,则________.
本章复习课
整合提升 练就四能
类型之1 锐角三角函数的定义
1.A
2.
3.
4.
类型之2 特殊角的三角函数值
5.(1) 解:原式.
(2) 原式.
类型之3 解直角三角形
6.B
7.(1) 解: ,,,
.
, .
.
(2) , .
.
,即,
.
8.(1) 4
(2) 解:设,则.
在中,,
即,解得,
,,
.
类型之4 解直角三角形的应用
9.C
10.(1) 45; 60
(2)
11.解:如答图,分别过点,作,交于点,.
第11题答图
四边形是梯形,且,
,,
四边形是矩形,
,.
在中, ,
.
在中,,
,
.
答:加固后坝底增加的宽度的长是.
12.(1) 解:如答图①,过点作的垂线分别交仰角、俯角线于点,,交水平线于点.
第12题答图①
在中, ,
.
,, ,
,
,
,
小杜最少需要下蹲才能被识别.
(2) 如答图②,过点作的垂线分别交仰角、俯角线于点,,交水平线于点.
第12题答图②
在中, ,
.
,, ,,
,
,
小若踮起脚尖后头顶的高度为,
小若头顶超出点的高度为,
踮起脚尖小若能被识别.
类型之5 解直角三角形与圆的结合
13.(1) 证明:如答图①,连接.
第13题答图①
,.
,,
,.
,.
又为的半径,
是的切线.
(2) 解:如答图②,连接,.
为的直径,
,即.
,,
.
在中,,
设,则,
,
,
解得(负值已舍去),
,
的半径为.
四边形是的内接四边形,
.
又,
,
,,,
.
第13题答图②
类型之6 数学活动
14.(1)
(2) 解:设,
, ,
.
,.
在中, ,
,
即,解得,
经检验是方程的解,且符合题意,
.
答:气球离地面的高度约是.
素养专练 培养三会
15.A 16.A
17.
