第二十九章 投影与视图 单元质量评估 (含答案)2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 第二十九章 投影与视图 单元质量评估 (含答案)2024-2025学年数学人教版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 315.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-02 21:40:44 | ||
图片预览


文档简介
第二十九章 投影与视图 质量评估
[时间:120分钟 分值:120分]
一、选择题(本大题共10个小题,每小题3分,共30分)
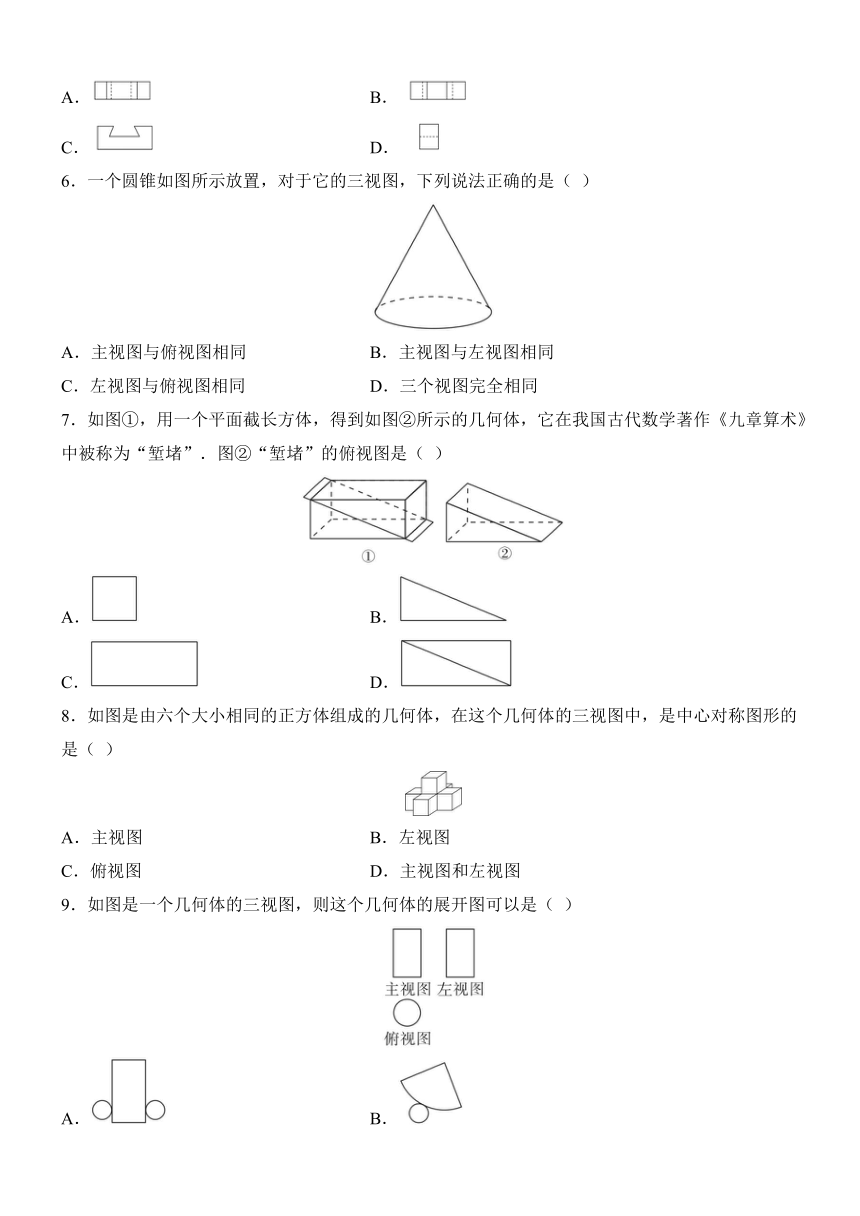
1.球在平面上的正投影是( )
A.圆面 B.椭圆面 C.点 D.线段
2.如图,晚上小明在路灯下沿路从处径直走到处,这一过程中他在地上的影子( )
第2题图
A.一直都在变短 B.先变短后变长
C.一直都在变长 D.先变长后变短
3.某同学学习了正方体的表面展开图后,在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字,还原成正方体后,“红”的对面是( )
第3题图
A.传 B.承 C.文 D.化
4.如图是由五个相同的正方体搭成的几何体,这个几何体的左视图是( )
A. B.
C. D.
5.榫卯是古代中国建筑、家具及其他器械的主要结构方式,是我国工艺文化精神的传承,凸出部分叫榫,凹进部分叫卯.如图是某个部件“卯”的实物图,它的主视图是( )
A. B.
C. D.
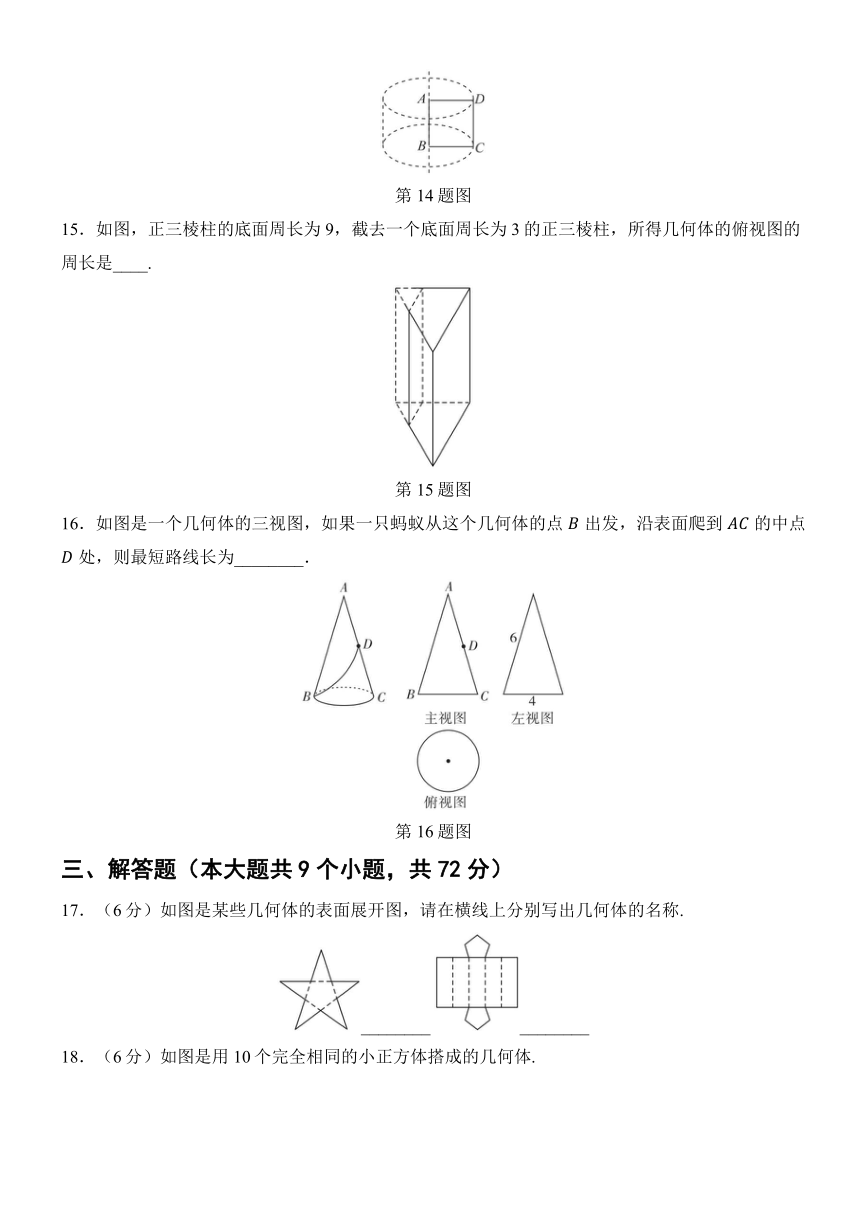
6.一个圆锥如图所示放置,对于它的三视图,下列说法正确的是( )
A.主视图与俯视图相同 B.主视图与左视图相同
C.左视图与俯视图相同 D.三个视图完全相同
7.如图①,用一个平面截长方体,得到如图②所示的几何体,它在我国古代数学著作《九章算术》中被称为“堑堵”.图②“堑堵”的俯视图是( )
A. B.
C. D.
8.如图是由六个大小相同的正方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( )
A.主视图 B.左视图
C.俯视图 D.主视图和左视图
9.如图是一个几何体的三视图,则这个几何体的展开图可以是( )
A. B.
C. D.
10.如图①,一个的平台上已经放了一个棱长为1的正方体,要得到一个几何体,其主视图和左视图如图②,平台上至少还需再放这样的正方体( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6个小题,每小题3分,共18分)
11.如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的俯视图的面积是____.
第11题图
12.如图是一个多面体的展开图,如果面在前面,从左面看是面,那么从上面看是面________________(填写字母).
第12题图
13.如图,平面直角坐标系内单位长度为,身高为的小强站在轴上的点处,他的前方处有一堵墙.若墙高,则站立的小强观察轴时,看不见的范围是______________.
第13题图
14.如图,正方形的边长为3,以直线为轴,将正方形旋转一周,所得几何体的主视图的周长是__.
第14题图
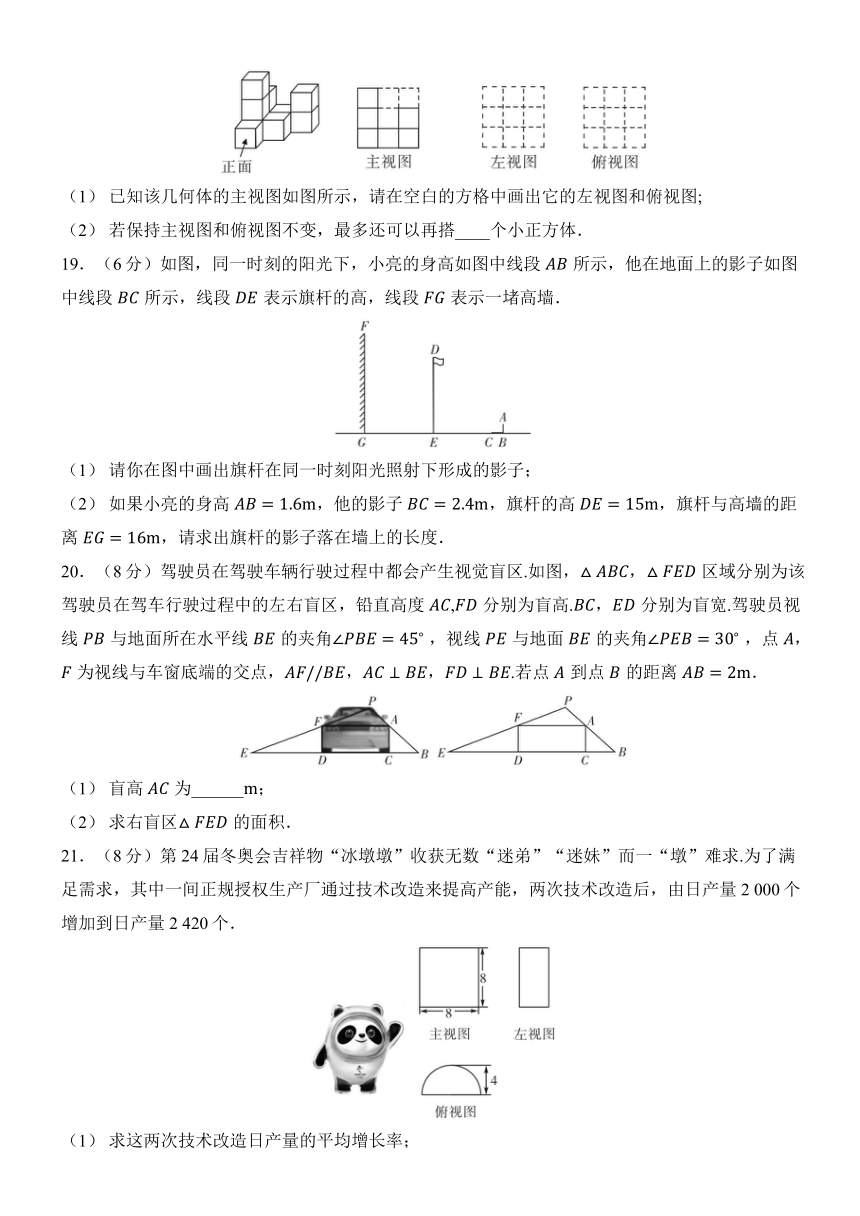
15.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是____.
第15题图
16.如图是一个几何体的三视图,如果一只蚂蚁从这个几何体的点出发,沿表面爬到的中点处,则最短路线长为________.
第16题图
三、解答题(本大题共9个小题,共72分)
17.(6分)如图是某些几何体的表面展开图,请在横线上分别写出几何体的名称.
________ ________
18.(6分)如图是用10个完全相同的小正方体搭成的几何体.
(1) 已知该几何体的主视图如图所示,请在空白的方格中画出它的左视图和俯视图;
(2) 若保持主视图和俯视图不变,最多还可以再搭____个小正方体.
19.(6分)如图,同一时刻的阳光下,小亮的身高如图中线段所示,他在地面上的影子如图中线段所示,线段表示旗杆的高,线段表示一堵高墙.
(1) 请你在图中画出旗杆在同一时刻阳光照射下形成的影子;
(2) 如果小亮的身高,他的影子,旗杆的高,旗杆与高墙的距离,请求出旗杆的影子落在墙上的长度.
20.(8分)驾驶员在驾驶车辆行驶过程中都会产生视觉盲区.如图,,区域分别为该驾驶员在驾车行驶过程中的左右盲区,铅直高度,分别为盲高.,分别为盲宽.驾驶员视线与地面所在水平线的夹角 ,视线与地面的夹角 ,点,为视线与车窗底端的交点,,,.若点到点的距离.
(1) 盲高为______;
(2) 求右盲区的面积.
21.(8分)第24届冬奥会吉祥物“冰墩墩”收获无数“迷弟”“迷妹”而一“墩”难求.为了满足需求,其中一间正规授权生产厂通过技术改造来提高产能,两次技术改造后,由日产量 2 000个增加到日产量2 420个.
(1) 求这两次技术改造日产量的平均增长率;
(2) 该生产厂家还设计了三视图如图所示的“冰墩墩”盲盒(单位:),请计算此类盲盒的表面积.
22.(9分)如图,在一个长、宽的矩形小操场上,王刚从地出发,沿着的路线以的速度跑向地.当他出发后,张华有东西需要交给他,就从地出发,沿王刚走的路线追赶.当张华跑到距离地的处时,他和王刚在阳光下的影子恰好重叠在同一条直线上,此时,处一根电线杆在阳光下的影子恰好落在对角线上.
(1) 求两人相距多少米(即的长);
(2) 求张华追赶王刚的速度(结果精确到).
23.(9分)中国古代运用“土圭之法”判别四季.夏至时日影最短,冬至时日影最长,春分和秋分时日影长度等于夏至和冬至日影长度的平均数.某地学生运用此法进行实践探索,如图,在示意图中,产生日影的杆子垂直于地面,长8尺.在夏至时,杆子在太阳光线照射下产生的日影为;在冬至时,杆子在太阳光线照射下产生的日影为.已知 , ,求春分和秋分时日影长度.(结果精确到0.1尺.参考数据:,,,,,)
24.(10分)如图①为一无盖的正方体纸盒,现将其剪开展成平面图形;如图②,已知展开图中每个正方形的边长为1.
(1) 求线段的长度;
(2) 试比较立体图中与展开图中的大小关系,并说明理由.
25.(10分)某数学兴趣小组测量碑林博物院内的一棵古树(古树四周有栅栏)高度的活动报告如下:
活动目的 利用“阳光和标杆”测量古树的高度(古树底部不可到达)
活动过程 步骤一:设计测量方案(小组讨论后,画出如图的测量示意图)
步骤二:准备测量工具 皮尺、侧倾器、标杆
步骤三:实地测量并记录数据是长的标杆,为古树落在地面上的影子,是同一时刻标杆落在地面上的影子 项目 第一次 第二次 平均值
步骤四:计算古树的高度
请结合以上信息解答下列问题:
(1) 表格中的值为____;
(2) 请完成步骤四:计算古树的高度.(参考数据:,,)
第二十九章质量评估
一、选择题(本大题共10个小题,每小题3分,共30分)
1.A 2.B 3.D 4.B 5.C 6.B 7.C 8.C 9.A 10.B
二、填空题(本大题共6个小题,每小题3分,共18分)
11.3
12.或
13.
14.18
15.8
16.
三、解答题(本大题共9个小题,共72分)
17.五棱锥; 五棱柱
18.(1) 解:如答图所示.
第18题答图
(2) 3
19.(1) 解:如答图,线段和表示旗杆在阳光下形成的影子.
第19题答图
(2) 过点作于点,如答图.
设旗杆的影子落在墙上的长度为,
由题意,得,
.
又,,
,,
,解得.
答:旗杆的影子落在墙上的长度为.
20.(1)
(2) 解:,,
,
又,
四边形是平行四边形,
,
在中, , ,
.,
.
21.(1) 解:设这两次技术改造日产量的平均增长率为,
根据题意,得,
解得,(不合题意,舍去).
答:这两次技术改造日产量的平均增长率为.
(2)
.
答:此类盲盒的表面积是.
22.(1) 解: 操场为矩形,且长为,宽为,
.
又 在同一时刻,阳光斜射角度相同,
,,
,即,
,
两人相距.
(2) ,
,,
王刚所跑的路程为.
张华所跑的路程为.
设张华的速度为,
根据题意,得,解得.
答:张华追赶王刚的速度约为.
23.解:在中,尺, ,
.
,
(尺).
在中,尺, ,
.
,
(尺).
(尺).
观察可知,春分和秋分时日影顶端为的中点,
(尺),
答:春分和秋分时日影长度约为9.2尺.
24.(1) 解:在中,
,,由勾股定理,得
.
(2) .理由如下:
立体图中为等腰直角三角形的一锐角,
.
在展开图中,连接,如答图.
第24题答图
由勾股定理,得,,由(1)可知.
可得,
由勾股定理的逆定理,可得为直角三角形.
又,
为等腰直角三角形,
,
.
25.(1) 6
(2) 解:如答图,过点作于点,
第25题答图
则四边形是矩形,
,.
设,
,,
,
,
,
,
,
,
答:古树的高度约为.
[时间:120分钟 分值:120分]
一、选择题(本大题共10个小题,每小题3分,共30分)
1.球在平面上的正投影是( )
A.圆面 B.椭圆面 C.点 D.线段
2.如图,晚上小明在路灯下沿路从处径直走到处,这一过程中他在地上的影子( )
第2题图
A.一直都在变短 B.先变短后变长
C.一直都在变长 D.先变长后变短
3.某同学学习了正方体的表面展开图后,在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字,还原成正方体后,“红”的对面是( )
第3题图
A.传 B.承 C.文 D.化
4.如图是由五个相同的正方体搭成的几何体,这个几何体的左视图是( )
A. B.
C. D.
5.榫卯是古代中国建筑、家具及其他器械的主要结构方式,是我国工艺文化精神的传承,凸出部分叫榫,凹进部分叫卯.如图是某个部件“卯”的实物图,它的主视图是( )
A. B.
C. D.
6.一个圆锥如图所示放置,对于它的三视图,下列说法正确的是( )
A.主视图与俯视图相同 B.主视图与左视图相同
C.左视图与俯视图相同 D.三个视图完全相同
7.如图①,用一个平面截长方体,得到如图②所示的几何体,它在我国古代数学著作《九章算术》中被称为“堑堵”.图②“堑堵”的俯视图是( )
A. B.
C. D.
8.如图是由六个大小相同的正方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( )
A.主视图 B.左视图
C.俯视图 D.主视图和左视图
9.如图是一个几何体的三视图,则这个几何体的展开图可以是( )
A. B.
C. D.
10.如图①,一个的平台上已经放了一个棱长为1的正方体,要得到一个几何体,其主视图和左视图如图②,平台上至少还需再放这样的正方体( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6个小题,每小题3分,共18分)
11.如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的俯视图的面积是____.
第11题图
12.如图是一个多面体的展开图,如果面在前面,从左面看是面,那么从上面看是面________________(填写字母).
第12题图
13.如图,平面直角坐标系内单位长度为,身高为的小强站在轴上的点处,他的前方处有一堵墙.若墙高,则站立的小强观察轴时,看不见的范围是______________.
第13题图
14.如图,正方形的边长为3,以直线为轴,将正方形旋转一周,所得几何体的主视图的周长是__.
第14题图
15.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是____.
第15题图
16.如图是一个几何体的三视图,如果一只蚂蚁从这个几何体的点出发,沿表面爬到的中点处,则最短路线长为________.
第16题图
三、解答题(本大题共9个小题,共72分)
17.(6分)如图是某些几何体的表面展开图,请在横线上分别写出几何体的名称.
________ ________
18.(6分)如图是用10个完全相同的小正方体搭成的几何体.
(1) 已知该几何体的主视图如图所示,请在空白的方格中画出它的左视图和俯视图;
(2) 若保持主视图和俯视图不变,最多还可以再搭____个小正方体.
19.(6分)如图,同一时刻的阳光下,小亮的身高如图中线段所示,他在地面上的影子如图中线段所示,线段表示旗杆的高,线段表示一堵高墙.
(1) 请你在图中画出旗杆在同一时刻阳光照射下形成的影子;
(2) 如果小亮的身高,他的影子,旗杆的高,旗杆与高墙的距离,请求出旗杆的影子落在墙上的长度.
20.(8分)驾驶员在驾驶车辆行驶过程中都会产生视觉盲区.如图,,区域分别为该驾驶员在驾车行驶过程中的左右盲区,铅直高度,分别为盲高.,分别为盲宽.驾驶员视线与地面所在水平线的夹角 ,视线与地面的夹角 ,点,为视线与车窗底端的交点,,,.若点到点的距离.
(1) 盲高为______;
(2) 求右盲区的面积.
21.(8分)第24届冬奥会吉祥物“冰墩墩”收获无数“迷弟”“迷妹”而一“墩”难求.为了满足需求,其中一间正规授权生产厂通过技术改造来提高产能,两次技术改造后,由日产量 2 000个增加到日产量2 420个.
(1) 求这两次技术改造日产量的平均增长率;
(2) 该生产厂家还设计了三视图如图所示的“冰墩墩”盲盒(单位:),请计算此类盲盒的表面积.
22.(9分)如图,在一个长、宽的矩形小操场上,王刚从地出发,沿着的路线以的速度跑向地.当他出发后,张华有东西需要交给他,就从地出发,沿王刚走的路线追赶.当张华跑到距离地的处时,他和王刚在阳光下的影子恰好重叠在同一条直线上,此时,处一根电线杆在阳光下的影子恰好落在对角线上.
(1) 求两人相距多少米(即的长);
(2) 求张华追赶王刚的速度(结果精确到).
23.(9分)中国古代运用“土圭之法”判别四季.夏至时日影最短,冬至时日影最长,春分和秋分时日影长度等于夏至和冬至日影长度的平均数.某地学生运用此法进行实践探索,如图,在示意图中,产生日影的杆子垂直于地面,长8尺.在夏至时,杆子在太阳光线照射下产生的日影为;在冬至时,杆子在太阳光线照射下产生的日影为.已知 , ,求春分和秋分时日影长度.(结果精确到0.1尺.参考数据:,,,,,)
24.(10分)如图①为一无盖的正方体纸盒,现将其剪开展成平面图形;如图②,已知展开图中每个正方形的边长为1.
(1) 求线段的长度;
(2) 试比较立体图中与展开图中的大小关系,并说明理由.
25.(10分)某数学兴趣小组测量碑林博物院内的一棵古树(古树四周有栅栏)高度的活动报告如下:
活动目的 利用“阳光和标杆”测量古树的高度(古树底部不可到达)
活动过程 步骤一:设计测量方案(小组讨论后,画出如图的测量示意图)
步骤二:准备测量工具 皮尺、侧倾器、标杆
步骤三:实地测量并记录数据是长的标杆,为古树落在地面上的影子,是同一时刻标杆落在地面上的影子 项目 第一次 第二次 平均值
步骤四:计算古树的高度
请结合以上信息解答下列问题:
(1) 表格中的值为____;
(2) 请完成步骤四:计算古树的高度.(参考数据:,,)
第二十九章质量评估
一、选择题(本大题共10个小题,每小题3分,共30分)
1.A 2.B 3.D 4.B 5.C 6.B 7.C 8.C 9.A 10.B
二、填空题(本大题共6个小题,每小题3分,共18分)
11.3
12.或
13.
14.18
15.8
16.
三、解答题(本大题共9个小题,共72分)
17.五棱锥; 五棱柱
18.(1) 解:如答图所示.
第18题答图
(2) 3
19.(1) 解:如答图,线段和表示旗杆在阳光下形成的影子.
第19题答图
(2) 过点作于点,如答图.
设旗杆的影子落在墙上的长度为,
由题意,得,
.
又,,
,,
,解得.
答:旗杆的影子落在墙上的长度为.
20.(1)
(2) 解:,,
,
又,
四边形是平行四边形,
,
在中, , ,
.,
.
21.(1) 解:设这两次技术改造日产量的平均增长率为,
根据题意,得,
解得,(不合题意,舍去).
答:这两次技术改造日产量的平均增长率为.
(2)
.
答:此类盲盒的表面积是.
22.(1) 解: 操场为矩形,且长为,宽为,
.
又 在同一时刻,阳光斜射角度相同,
,,
,即,
,
两人相距.
(2) ,
,,
王刚所跑的路程为.
张华所跑的路程为.
设张华的速度为,
根据题意,得,解得.
答:张华追赶王刚的速度约为.
23.解:在中,尺, ,
.
,
(尺).
在中,尺, ,
.
,
(尺).
(尺).
观察可知,春分和秋分时日影顶端为的中点,
(尺),
答:春分和秋分时日影长度约为9.2尺.
24.(1) 解:在中,
,,由勾股定理,得
.
(2) .理由如下:
立体图中为等腰直角三角形的一锐角,
.
在展开图中,连接,如答图.
第24题答图
由勾股定理,得,,由(1)可知.
可得,
由勾股定理的逆定理,可得为直角三角形.
又,
为等腰直角三角形,
,
.
25.(1) 6
(2) 解:如答图,过点作于点,
第25题答图
则四边形是矩形,
,.
设,
,,
,
,
,
,
,
,
答:古树的高度约为.
