第二十六章 反比例函数 单元复习课(含答案) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 第二十六章 反比例函数 单元复习课(含答案) 2024-2025学年数学人教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 149.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-02 00:00:00 | ||
图片预览

文档简介
第二十六章 反比例函数 复习课
整合提升 练就四能
类型之1 反比例函数的概念
1.[2023岳阳模拟]若函数是关于的反比例函数,则____.
类型之2 反比例函数的图象与性质
2.[2023天津]若点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B.
C. D.
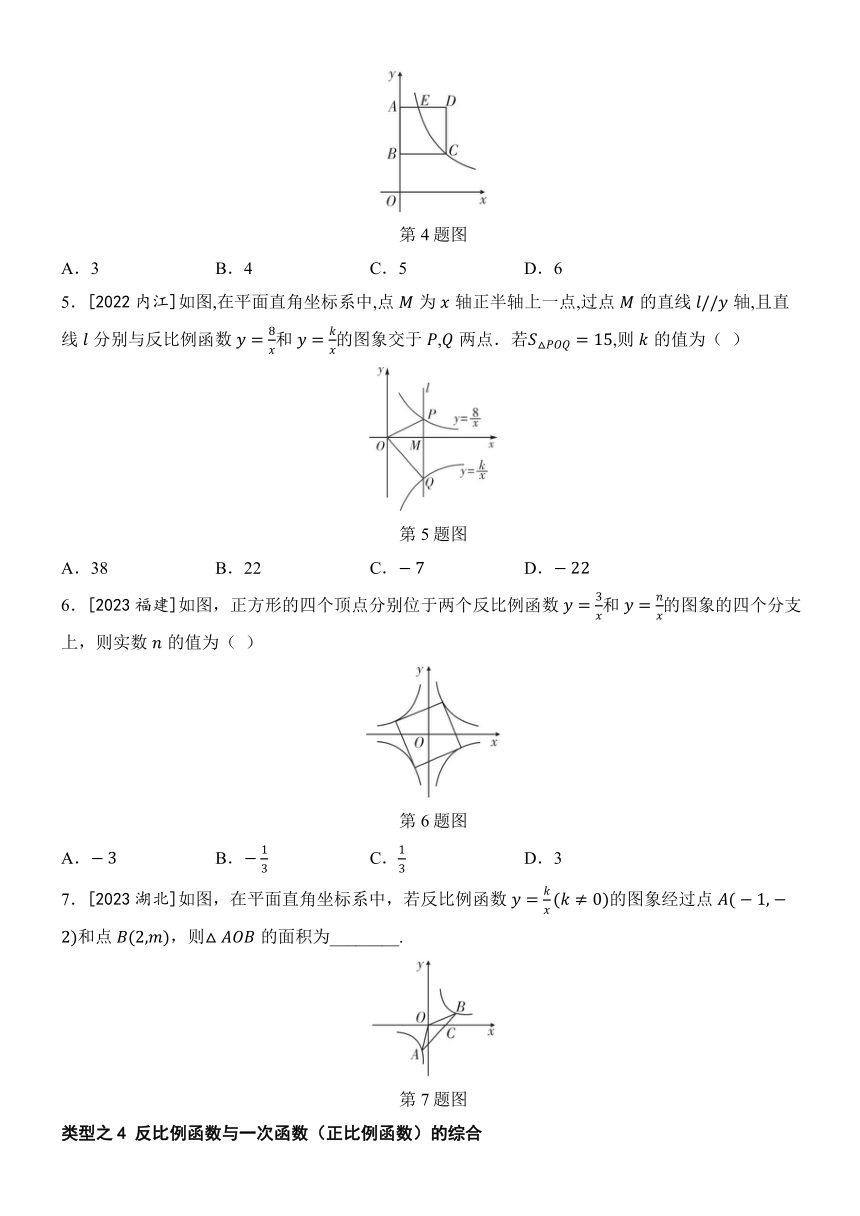
3.[2023安徽]已知反比例函数在第一象限内的图象与一次函数的图象如图所示,则函数的图象可能为( )
A. B.
C. D.
类型之3 反比例函数的几何意义
4.[2023牡丹江]如图,正方形的顶点,在轴上,反比例函数的图象经过点和的中点.若,则的值是( )
第4题图
A.3 B.4 C.5 D.6
5.[2022内江]如图,在平面直角坐标系中,点为轴正半轴上一点,过点的直线轴,且直线分别与反比例函数和的图象交于,两点.若,则的值为( )
第5题图
A.38 B.22 C. D.
6.[2023福建]如图,正方形的四个顶点分别位于两个反比例函数和的图象的四个分支上,则实数的值为( )
第6题图
A. B. C. D.3
7.[2023湖北]如图,在平面直角坐标系中,若反比例函数的图象经过点和点,则的面积为________.
第7题图
类型之4 反比例函数与一次函数(正比例函数)的综合
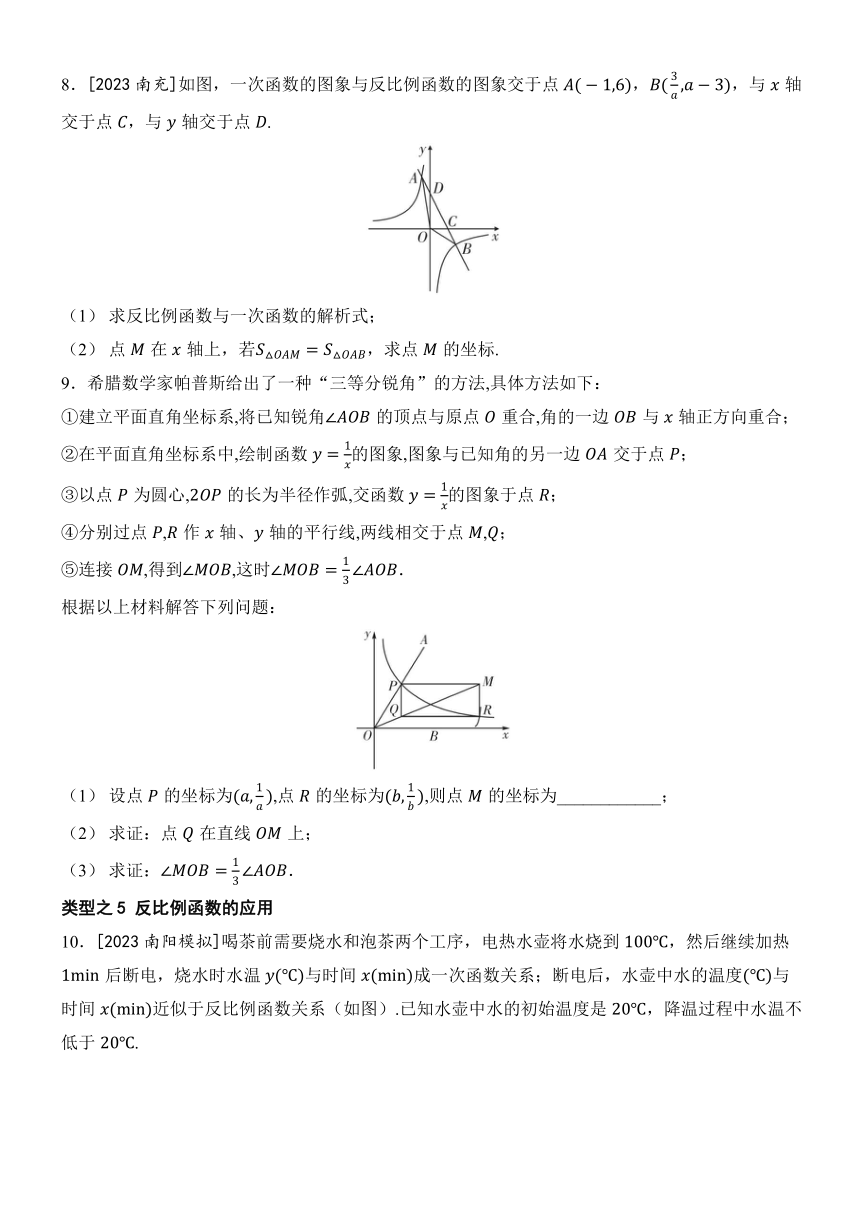
8.[2023南充]如图,一次函数的图象与反比例函数的图象交于点,,与轴交于点,与轴交于点.
(1) 求反比例函数与一次函数的解析式;
(2) 点在轴上,若,求点的坐标.
9.希腊数学家帕普斯给出了一种“三等分锐角”的方法,具体方法如下:
①建立平面直角坐标系,将已知锐角的顶点与原点重合,角的一边与轴正方向重合;
②在平面直角坐标系中,绘制函数的图象,图象与已知角的另一边交于点;
③以点为圆心,的长为半径作弧,交函数的图象于点;
④分别过点,作轴、轴的平行线,两线相交于点,;
⑤连接,得到,这时.
根据以上材料解答下列问题:
(1) 设点的坐标为,点的坐标为,则点的坐标为____________;
(2) 求证:点在直线上;
(3) 求证:.
类型之5 反比例函数的应用
10.[2023南阳模拟]喝茶前需要烧水和泡茶两个工序,电热水壶将水烧到,然后继续加热后断电,烧水时水温与时间成一次函数关系;断电后,水壶中水的温度与时间近似于反比例函数关系(如图).已知水壶中水的初始温度是,降温过程中水温不低于.
(1) 分别求出图中段和段所对应的函数解析式;
(2) 从水壶中的水烧开降到就可以进行泡茶,问从水烧开到泡茶需要等待多长时间?
素养专练 培养三会
11.[2023衡阳模拟]【模型观念】下列图形中,阴影部分的面积相等的是( )
A.①② B.②③ C.①④ D.③④
12.[2023黑龙江]【模型观念,推理能力】如图,是等腰三角形,过原点,底边轴,双曲线过,两点,过点作轴交双曲线于点.若,则的值是( )
B. C. D.
本章复习课
整合提升 练就四能
类型之1 反比例函数的概念
1.2
类型之2 反比例函数的图象与性质
2.D 3.A
类型之3 反比例函数的几何意义
4.B 5.D 6.A
7.
类型之4 反比例函数与一次函数(正比例函数)的综合
8.(1) 解:由题意,设反比例函数、一次函数的解析式分别为,.
点在反比例函数的图象上,
.
反比例函数的解析式为.
点在反比例函数图象上,
,.
.
点,在一次函数的图象上,
一次函数的解析式为.
(2) 设点.
由(1),得一次函数交轴于点,,
.
点在轴上,
.
又,.
.
点的坐标为或.
9.(1)
(2) 证明:由(1),得.
设直线的解析式为.
,,.
直线的解析式为.
当时,,
点在直线上.
(3) 如答图,连接,交于点.
第9题答图
易知四边形为矩形,
,,,
,,
.
又,,
,
,
.
类型之5 反比例函数的应用
10.(1) 解:当停止加热时,设.
把代入,得,
解得,
.
当时,解得,
点的坐标为,
点的坐标为.
当加热烧水时,设,
把点的坐标代入,得,
解得,
当加热烧水时,段所对应的函数解析式为;
当停止加热时,段所对应的函数解析式为.
(2) 把代入,得,
因此从水开到泡茶需要等待.
素养专练 培养三会
11.D 12.C
整合提升 练就四能
类型之1 反比例函数的概念
1.[2023岳阳模拟]若函数是关于的反比例函数,则____.
类型之2 反比例函数的图象与性质
2.[2023天津]若点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B.
C. D.
3.[2023安徽]已知反比例函数在第一象限内的图象与一次函数的图象如图所示,则函数的图象可能为( )
A. B.
C. D.
类型之3 反比例函数的几何意义
4.[2023牡丹江]如图,正方形的顶点,在轴上,反比例函数的图象经过点和的中点.若,则的值是( )
第4题图
A.3 B.4 C.5 D.6
5.[2022内江]如图,在平面直角坐标系中,点为轴正半轴上一点,过点的直线轴,且直线分别与反比例函数和的图象交于,两点.若,则的值为( )
第5题图
A.38 B.22 C. D.
6.[2023福建]如图,正方形的四个顶点分别位于两个反比例函数和的图象的四个分支上,则实数的值为( )
第6题图
A. B. C. D.3
7.[2023湖北]如图,在平面直角坐标系中,若反比例函数的图象经过点和点,则的面积为________.
第7题图
类型之4 反比例函数与一次函数(正比例函数)的综合
8.[2023南充]如图,一次函数的图象与反比例函数的图象交于点,,与轴交于点,与轴交于点.
(1) 求反比例函数与一次函数的解析式;
(2) 点在轴上,若,求点的坐标.
9.希腊数学家帕普斯给出了一种“三等分锐角”的方法,具体方法如下:
①建立平面直角坐标系,将已知锐角的顶点与原点重合,角的一边与轴正方向重合;
②在平面直角坐标系中,绘制函数的图象,图象与已知角的另一边交于点;
③以点为圆心,的长为半径作弧,交函数的图象于点;
④分别过点,作轴、轴的平行线,两线相交于点,;
⑤连接,得到,这时.
根据以上材料解答下列问题:
(1) 设点的坐标为,点的坐标为,则点的坐标为____________;
(2) 求证:点在直线上;
(3) 求证:.
类型之5 反比例函数的应用
10.[2023南阳模拟]喝茶前需要烧水和泡茶两个工序,电热水壶将水烧到,然后继续加热后断电,烧水时水温与时间成一次函数关系;断电后,水壶中水的温度与时间近似于反比例函数关系(如图).已知水壶中水的初始温度是,降温过程中水温不低于.
(1) 分别求出图中段和段所对应的函数解析式;
(2) 从水壶中的水烧开降到就可以进行泡茶,问从水烧开到泡茶需要等待多长时间?
素养专练 培养三会
11.[2023衡阳模拟]【模型观念】下列图形中,阴影部分的面积相等的是( )
A.①② B.②③ C.①④ D.③④
12.[2023黑龙江]【模型观念,推理能力】如图,是等腰三角形,过原点,底边轴,双曲线过,两点,过点作轴交双曲线于点.若,则的值是( )
B. C. D.
本章复习课
整合提升 练就四能
类型之1 反比例函数的概念
1.2
类型之2 反比例函数的图象与性质
2.D 3.A
类型之3 反比例函数的几何意义
4.B 5.D 6.A
7.
类型之4 反比例函数与一次函数(正比例函数)的综合
8.(1) 解:由题意,设反比例函数、一次函数的解析式分别为,.
点在反比例函数的图象上,
.
反比例函数的解析式为.
点在反比例函数图象上,
,.
.
点,在一次函数的图象上,
一次函数的解析式为.
(2) 设点.
由(1),得一次函数交轴于点,,
.
点在轴上,
.
又,.
.
点的坐标为或.
9.(1)
(2) 证明:由(1),得.
设直线的解析式为.
,,.
直线的解析式为.
当时,,
点在直线上.
(3) 如答图,连接,交于点.
第9题答图
易知四边形为矩形,
,,,
,,
.
又,,
,
,
.
类型之5 反比例函数的应用
10.(1) 解:当停止加热时,设.
把代入,得,
解得,
.
当时,解得,
点的坐标为,
点的坐标为.
当加热烧水时,设,
把点的坐标代入,得,
解得,
当加热烧水时,段所对应的函数解析式为;
当停止加热时,段所对应的函数解析式为.
(2) 把代入,得,
因此从水开到泡茶需要等待.
素养专练 培养三会
11.D 12.C
