期末质量评估(含答案) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 期末质量评估(含答案) 2024-2025学年数学人教版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 314.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-02 21:50:15 | ||
图片预览


文档简介
期末质量评估
[时间:120分钟 分值:120分]
一、选择题(本大题共10个小题,每小题3分,共30分)
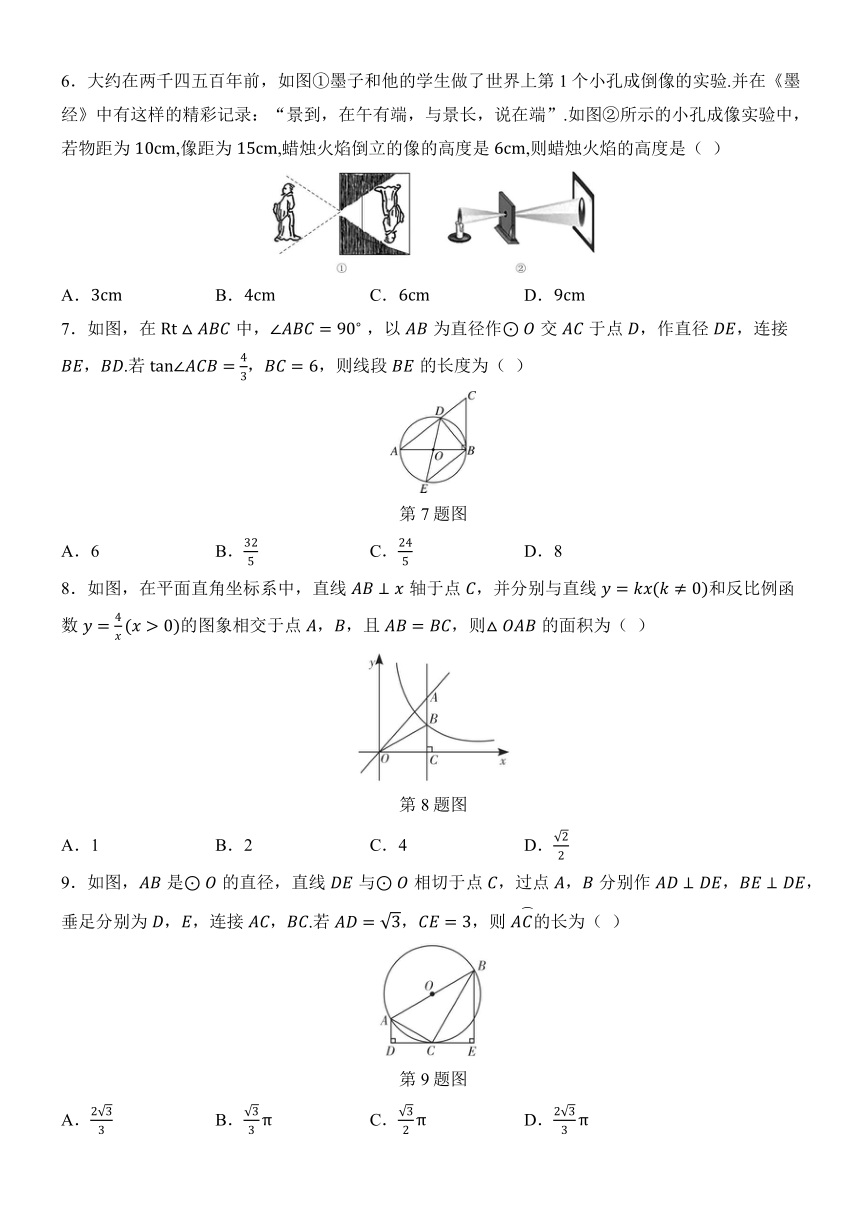
1.如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是( )
A. B. C. D.
2.已知 为锐角,,则( )
A. B. C. D.
3.若点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B.
C. D.
4.二次函数的图象如图所示,则反比例函数与一次函数在同一平面直角坐标系中的大致图象为( )
A. B.
C. D.
5.如图,在中,,分别是和上的点,.若,则( )
A. B. C. D.
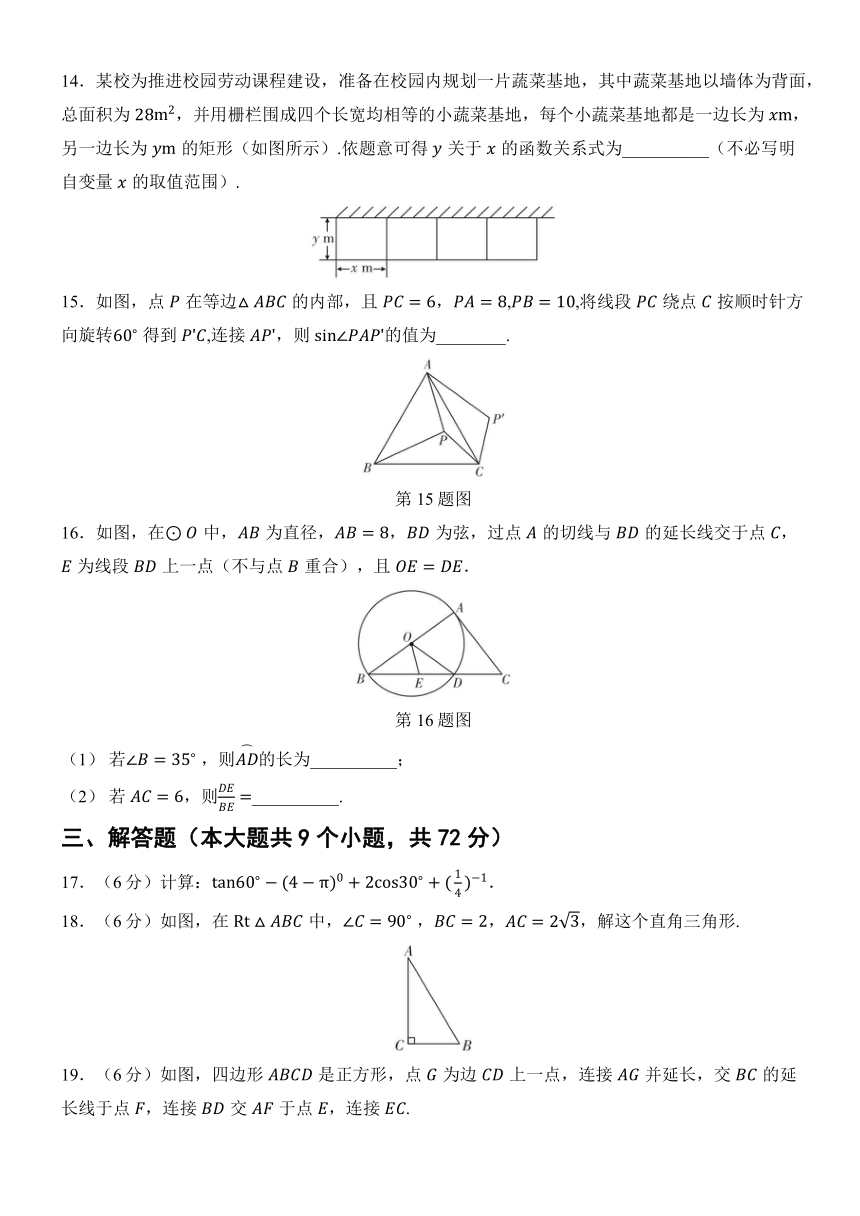
6.大约在两千四五百年前,如图①墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图②所示的小孔成像实验中,若物距为,像距为,蜡烛火焰倒立的像的高度是,则蜡烛火焰的高度是( )
A. B. C. D.
7.如图,在中, ,以为直径作交于点,作直径,连接,.若 ,,则线段的长度为( )
第7题图
A.6 B. C. D.8
8.如图,在平面直角坐标系中,直线轴于点,并分别与直线和反比例函数的图象相交于点,,且,则的面积为( )
第8题图
A.1 B.2 C.4 D.
9.如图,是的直径,直线与相切于点,过点,分别作,,垂足分别为,,连接,.若,,则的长为( )
第9题图
A. B. C. D.
10.如图,在平面直角坐标系中,矩形的顶点,分别在轴、轴上,对角线轴,反比例函数的图象经过矩形对角线的交点.若点,,则的值为( )
第10题图
A.16 B.20 C.32 D.40
二、填空题(本大题共6个小题,每小题3分,共18分)
11.如图,在中,点在上,且,则________.
第11题图
12.如图,在某小区内拐角处的一段道路上,有一儿童在处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的处驶来,,与相交于点,已知,,,,则汽车从处前行的距离____时,才能发现处的儿童.
第12题图
13.如图,是反比例函数的图象上一点,过点作轴于点,且为线段的中点.若点为轴上任意一点,且的面积为4,则________.
第13题图
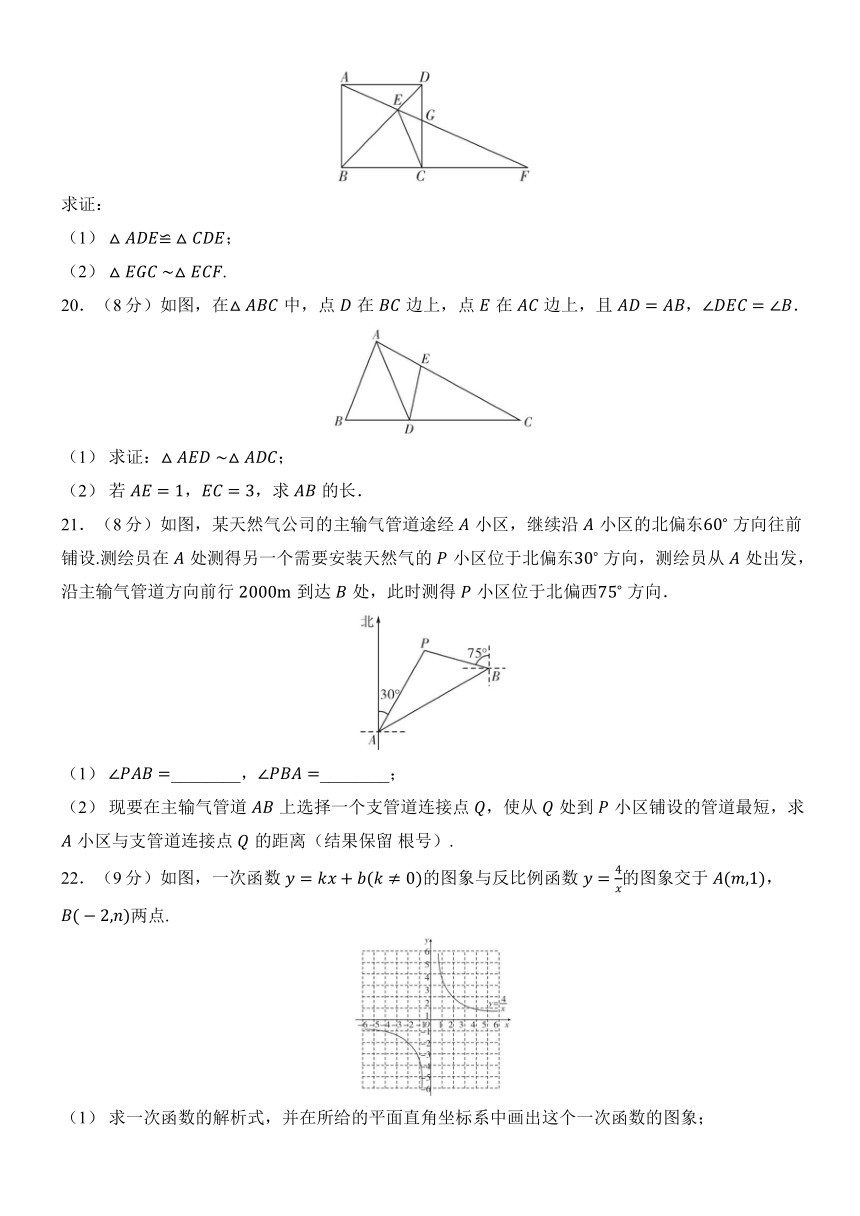
14.某校为推进校园劳动课程建设,准备在校园内规划一片蔬菜基地,其中蔬菜基地以墙体为背面,总面积为,并用栅栏围成四个长宽均相等的小蔬菜基地,每个小蔬菜基地都是一边长为,另一边长为的矩形(如图所示).依题意可得关于的函数关系式为__________(不必写明自变量的取值范围).
15.如图,点在等边的内部,且,,,将线段绕点按顺时针方向旋转 得到,连接,则的值为________.
第15题图
16.如图,在中,为直径,,为弦,过点的切线与的延长线交于点,为线段上一点(不与点重合),且.
第16题图
(1) 若 ,则的长为__________;
(2) 若,则__________.
三、解答题(本大题共9个小题,共72分)
17.(6分)计算:.
18.(6分)如图,在中, ,,,解这个直角三角形.
19.(6分)如图,四边形是正方形,点为边上一点,连接并延长,交的延长线于点,连接交于点,连接.
求证:
(1) ;
(2) .
20.(8分)如图,在中,点在边上,点在边上,且,.
(1) 求证:;
(2) 若,,求的长.
21.(8分)如图,某天然气公司的主输气管道途经小区,继续沿小区的北偏东 方向往前铺设.测绘员在处测得另一个需要安装天然气的小区位于北偏东 方向,测绘员从处出发,沿主输气管道方向前行到达处,此时测得小区位于北偏西 方向.
(1) ________,________;
(2) 现要在主输气管道上选择一个支管道连接点,使从处到小区铺设的管道最短,求小区与支管道连接点的距离(结果保留 根号).
22.(9分)如图,一次函数的图象与反比例函数的图象交于,两点.
(1) 求一次函数的解析式,并在所给的平面直角坐标系中画出这个一次函数的图象;
(2) 观察图象,直接写出不等式的解集;
(3) 设直线与轴交于点,若为轴上的一动点,连接,,当的面积为时,求点的坐标.
23.(9分)某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图所示.
(1) 由三视图可知,密封纸盒的形状是__________;
(2) 请你根据图中的数据,计算这个密封纸盒的表面积.(结果保留根号)
24.(10分)如图,内接于,为直径,于点,延长交于点,过点作的切线,与的延长线交于点,连接交于点,连接.
(1) 求证:四边形为矩形;
(2) 求证:;
(3) 若(为常数),求(用含的代数式表示).
25.(10分)定义:在平面直角坐标系中,若在函数图象上存在一点,绕原点顺时针旋转 后的对应点(点与点不重合)仍在此函数图象上,则称这个函数为“凡尔赛函数”,其中点称为这个函数的“凡尔赛点”,点叫做点的“后凡尔赛点”.
(1) 函数,,,其中是“凡尔赛函数”的是____(填序号);
(2) 若一次函数是“凡尔赛函数”,点(为整数)是这个函数的“凡尔赛点”,求的值;
(3) 若点是二次函数(其中,,为常数,)的“凡尔赛点”,点为点的“后凡尔赛点”,此二次函数图象与轴交于,两点,由,,,为顶点构成的四边形面积记为,求的取值范围.
期末质量评估
一、选择题(本大题共10个小题,每小题3分,共30分)
1.A 2.C 3.C 4.D 5.D 6.B 7.B 8.B 9.D 10.B
二、填空题(本大题共6个小题,每小题3分,共18分)
11.
12.5.75
13.
14.
15.
16.(1)
(2)
三、解答题(本大题共9个小题,共72分)
17.解:原式
.
18.解:在中, ,,,
,
,
,
.
19.(1) 证明: 四边形是正方形,
, .
又,;
(2) ,,.
四边形是正方形,点在的延长线上,
,,,
又,.
20.(1) 证明:,.
,,
.
又,.
(2) 解:,,即,
或(舍去).
又,.
21.(1) ;
(2) 解:如答图,过点作于点.
第21题答图
设,
在中, ,,
在中, ,
.
,,解得,
.
答:小区与支管道连接点的距离为.
22.(1) 解: 反比例函数的图象经过,两点,
,,,.
将,的坐标代入,
得解得
一次函数的解析式为,该函数的图象如答图所示.
(2) 不等式的解集是或.
(3) 如答图,设直线交轴于点.
第22题答图
在中,当时,,.
当时,,,.
,,.
,,
解得或.
点的坐标为或.
23.(1) 正六棱柱
(2) 解:由图中数据可知:六棱柱的高为,底面边长为,
六棱柱的侧面积为,
密封纸盒的上、下底面面积为6个等边三角形的面积,如答图.
第23题答图
,
底面面积为,
答:这个密封纸盒的表面积为.
24.(1) 证明:,
.
为直径, , .
为的切线,
.
,
四边形为矩形.
(2) 证明:过圆心,,
,
.
又,
,
,.
(3) 解: 四边形为矩形,
,
,.
设,.
,,是的中位线,.
在中,,
.
又和都是所对的圆周角,,
.
25.(1) ③
(2) 解: 点是一次函数的“凡尔赛点”,点的“后凡尔赛点”为,
.
当时,,满足条件;
当时,
关于的一元二次方程有实数根,,
解得.
又为整数,或,
当时,,解得,;
当时,,解得(舍去),.
综上所述,的值为,1,或.
(3) 点是二次函数(其中,,为常数,)的“凡尔赛点”,
“后凡尔赛点”的坐标为,
解得.
令,得,
.
令,则,
,,解得,
,,.
.
[时间:120分钟 分值:120分]
一、选择题(本大题共10个小题,每小题3分,共30分)
1.如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是( )
A. B. C. D.
2.已知 为锐角,,则( )
A. B. C. D.
3.若点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B.
C. D.
4.二次函数的图象如图所示,则反比例函数与一次函数在同一平面直角坐标系中的大致图象为( )
A. B.
C. D.
5.如图,在中,,分别是和上的点,.若,则( )
A. B. C. D.
6.大约在两千四五百年前,如图①墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图②所示的小孔成像实验中,若物距为,像距为,蜡烛火焰倒立的像的高度是,则蜡烛火焰的高度是( )
A. B. C. D.
7.如图,在中, ,以为直径作交于点,作直径,连接,.若 ,,则线段的长度为( )
第7题图
A.6 B. C. D.8
8.如图,在平面直角坐标系中,直线轴于点,并分别与直线和反比例函数的图象相交于点,,且,则的面积为( )
第8题图
A.1 B.2 C.4 D.
9.如图,是的直径,直线与相切于点,过点,分别作,,垂足分别为,,连接,.若,,则的长为( )
第9题图
A. B. C. D.
10.如图,在平面直角坐标系中,矩形的顶点,分别在轴、轴上,对角线轴,反比例函数的图象经过矩形对角线的交点.若点,,则的值为( )
第10题图
A.16 B.20 C.32 D.40
二、填空题(本大题共6个小题,每小题3分,共18分)
11.如图,在中,点在上,且,则________.
第11题图
12.如图,在某小区内拐角处的一段道路上,有一儿童在处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的处驶来,,与相交于点,已知,,,,则汽车从处前行的距离____时,才能发现处的儿童.
第12题图
13.如图,是反比例函数的图象上一点,过点作轴于点,且为线段的中点.若点为轴上任意一点,且的面积为4,则________.
第13题图
14.某校为推进校园劳动课程建设,准备在校园内规划一片蔬菜基地,其中蔬菜基地以墙体为背面,总面积为,并用栅栏围成四个长宽均相等的小蔬菜基地,每个小蔬菜基地都是一边长为,另一边长为的矩形(如图所示).依题意可得关于的函数关系式为__________(不必写明自变量的取值范围).
15.如图,点在等边的内部,且,,,将线段绕点按顺时针方向旋转 得到,连接,则的值为________.
第15题图
16.如图,在中,为直径,,为弦,过点的切线与的延长线交于点,为线段上一点(不与点重合),且.
第16题图
(1) 若 ,则的长为__________;
(2) 若,则__________.
三、解答题(本大题共9个小题,共72分)
17.(6分)计算:.
18.(6分)如图,在中, ,,,解这个直角三角形.
19.(6分)如图,四边形是正方形,点为边上一点,连接并延长,交的延长线于点,连接交于点,连接.
求证:
(1) ;
(2) .
20.(8分)如图,在中,点在边上,点在边上,且,.
(1) 求证:;
(2) 若,,求的长.
21.(8分)如图,某天然气公司的主输气管道途经小区,继续沿小区的北偏东 方向往前铺设.测绘员在处测得另一个需要安装天然气的小区位于北偏东 方向,测绘员从处出发,沿主输气管道方向前行到达处,此时测得小区位于北偏西 方向.
(1) ________,________;
(2) 现要在主输气管道上选择一个支管道连接点,使从处到小区铺设的管道最短,求小区与支管道连接点的距离(结果保留 根号).
22.(9分)如图,一次函数的图象与反比例函数的图象交于,两点.
(1) 求一次函数的解析式,并在所给的平面直角坐标系中画出这个一次函数的图象;
(2) 观察图象,直接写出不等式的解集;
(3) 设直线与轴交于点,若为轴上的一动点,连接,,当的面积为时,求点的坐标.
23.(9分)某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图所示.
(1) 由三视图可知,密封纸盒的形状是__________;
(2) 请你根据图中的数据,计算这个密封纸盒的表面积.(结果保留根号)
24.(10分)如图,内接于,为直径,于点,延长交于点,过点作的切线,与的延长线交于点,连接交于点,连接.
(1) 求证:四边形为矩形;
(2) 求证:;
(3) 若(为常数),求(用含的代数式表示).
25.(10分)定义:在平面直角坐标系中,若在函数图象上存在一点,绕原点顺时针旋转 后的对应点(点与点不重合)仍在此函数图象上,则称这个函数为“凡尔赛函数”,其中点称为这个函数的“凡尔赛点”,点叫做点的“后凡尔赛点”.
(1) 函数,,,其中是“凡尔赛函数”的是____(填序号);
(2) 若一次函数是“凡尔赛函数”,点(为整数)是这个函数的“凡尔赛点”,求的值;
(3) 若点是二次函数(其中,,为常数,)的“凡尔赛点”,点为点的“后凡尔赛点”,此二次函数图象与轴交于,两点,由,,,为顶点构成的四边形面积记为,求的取值范围.
期末质量评估
一、选择题(本大题共10个小题,每小题3分,共30分)
1.A 2.C 3.C 4.D 5.D 6.B 7.B 8.B 9.D 10.B
二、填空题(本大题共6个小题,每小题3分,共18分)
11.
12.5.75
13.
14.
15.
16.(1)
(2)
三、解答题(本大题共9个小题,共72分)
17.解:原式
.
18.解:在中, ,,,
,
,
,
.
19.(1) 证明: 四边形是正方形,
, .
又,;
(2) ,,.
四边形是正方形,点在的延长线上,
,,,
又,.
20.(1) 证明:,.
,,
.
又,.
(2) 解:,,即,
或(舍去).
又,.
21.(1) ;
(2) 解:如答图,过点作于点.
第21题答图
设,
在中, ,,
在中, ,
.
,,解得,
.
答:小区与支管道连接点的距离为.
22.(1) 解: 反比例函数的图象经过,两点,
,,,.
将,的坐标代入,
得解得
一次函数的解析式为,该函数的图象如答图所示.
(2) 不等式的解集是或.
(3) 如答图,设直线交轴于点.
第22题答图
在中,当时,,.
当时,,,.
,,.
,,
解得或.
点的坐标为或.
23.(1) 正六棱柱
(2) 解:由图中数据可知:六棱柱的高为,底面边长为,
六棱柱的侧面积为,
密封纸盒的上、下底面面积为6个等边三角形的面积,如答图.
第23题答图
,
底面面积为,
答:这个密封纸盒的表面积为.
24.(1) 证明:,
.
为直径, , .
为的切线,
.
,
四边形为矩形.
(2) 证明:过圆心,,
,
.
又,
,
,.
(3) 解: 四边形为矩形,
,
,.
设,.
,,是的中位线,.
在中,,
.
又和都是所对的圆周角,,
.
25.(1) ③
(2) 解: 点是一次函数的“凡尔赛点”,点的“后凡尔赛点”为,
.
当时,,满足条件;
当时,
关于的一元二次方程有实数根,,
解得.
又为整数,或,
当时,,解得,;
当时,,解得(舍去),.
综上所述,的值为,1,或.
(3) 点是二次函数(其中,,为常数,)的“凡尔赛点”,
“后凡尔赛点”的坐标为,
解得.
令,得,
.
令,则,
,,解得,
,,.
.
同课章节目录
