6.3 实数的课件(共3课时)
图片预览









文档简介
课件37张PPT。6.3 实数第1课时 实数的概念
第2课时 实数的性质与运算
专题 实数的概念与计算第1课时 实数的概念还有其它类型的小数吗?这些都是无限不循环小数实数的概念和分类一、对无理数的认识:
1、无限不循环小数叫无理数;
2、无理数也有正负之分.例如:
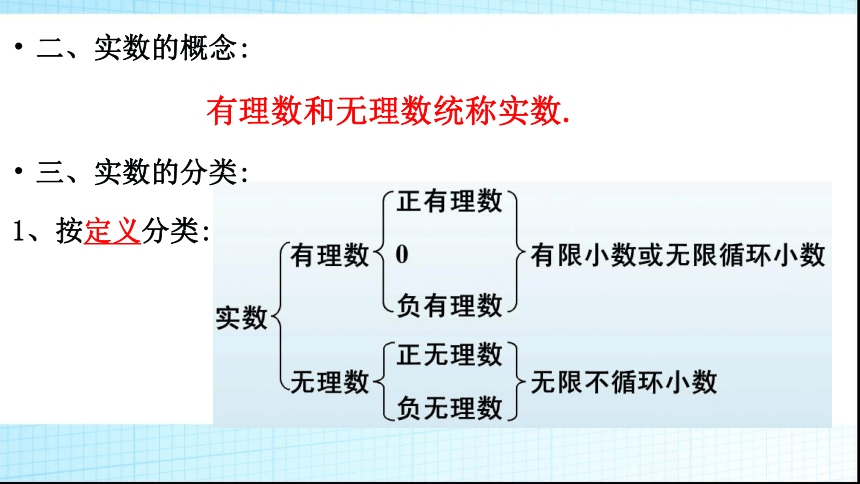
二、实数的概念:
有理数和无理数统称实数.
三、实数的分类:
1、按定义分类:
2、按性质分类:练习:
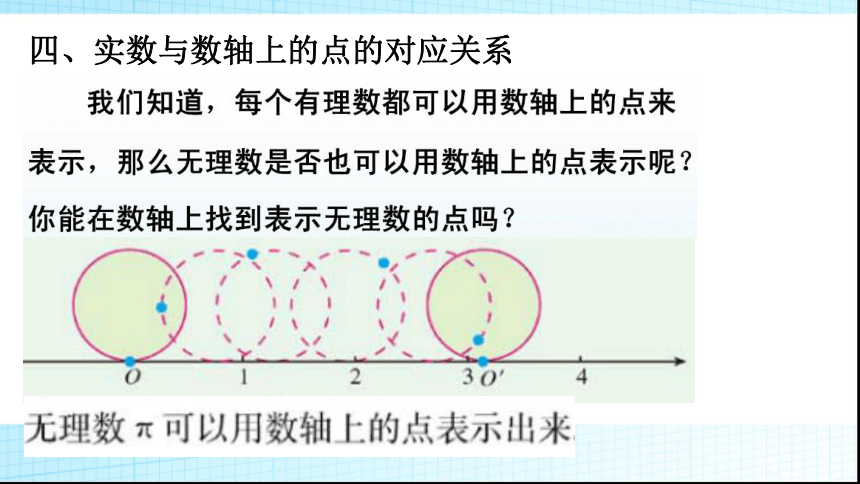
1.将下列各数填入相应的集合内:四、实数与数轴上的点的对应关系事实上,每一个无理数都可以用数轴上的一个点表示出来.实数与数轴上的点的对应关系①实数与数轴上的点是一一对应的,即:
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一个点都表示一个实数.
②数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大,即:
数轴上从左到右的点,对应着从小到大的实数.例2、下列说法不正确的是( )
A、数轴上的点可以表示有理数,也可以表示无理数;
B、数轴上的某一点可以同时表示有理数和无理数;
C、数轴上的所有点表示的数全是实数;
D、有理数都能在数轴上表示出来,而数轴上的点表示的数不一定是有理数.第2课时 实数的性质与运算有理数和无理数统称实数.实数与数轴上的点是一一对应的相反数:只有符号不同的两个数叫做互为相反数
一般地,a和-a互为相反数.绝对值:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作:|a|
a与-a的绝对值相等,在数轴上对应的点关于原点对称.实数的性质有理数关于相反数和绝对值的意义同样适用于实数!例2、实数a,b在数轴上的位置如图所示,
化简|a+b|-|b-a|+a.3、已知实数a,b,c在数轴上的位置如图所示,化简:
|a+b|-|b+c|+|b-c|-|b|.实数的运算实数之间不仅可以进行加、减、乘、除(除数不为0)、乘方运算,而且正数和0可以进行开平方(偶次方)运算,任意一个实数可以进行开立方(奇次方)运算;
在进行实数的运算时,有理数的运算法则及运算性质同样适用.如果实数运算时,遇到无理数并且需要求出结果的近似值时,可以按照所要求的精确度用相应的近似有限小数去代替无理数(一般比精确度多一位小数),再进行计算. 实数的运算怎样进行?二、准确把握实数的性质三、掌握实数的运算四、实数在日常生活中的应用例6、学校有一个面积为100 m2的圆形花坛,为了需要,现将花坛的半径增加2 m,重建一个新的花坛.求新建花坛的半径.
第2课时 实数的性质与运算
专题 实数的概念与计算第1课时 实数的概念还有其它类型的小数吗?这些都是无限不循环小数实数的概念和分类一、对无理数的认识:
1、无限不循环小数叫无理数;
2、无理数也有正负之分.例如:
二、实数的概念:
有理数和无理数统称实数.
三、实数的分类:
1、按定义分类:
2、按性质分类:练习:
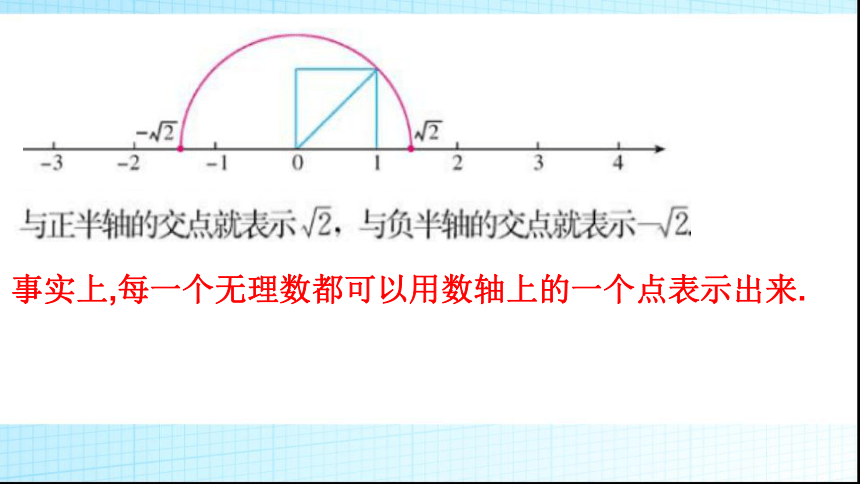
1.将下列各数填入相应的集合内:四、实数与数轴上的点的对应关系事实上,每一个无理数都可以用数轴上的一个点表示出来.实数与数轴上的点的对应关系①实数与数轴上的点是一一对应的,即:
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一个点都表示一个实数.
②数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大,即:
数轴上从左到右的点,对应着从小到大的实数.例2、下列说法不正确的是( )
A、数轴上的点可以表示有理数,也可以表示无理数;
B、数轴上的某一点可以同时表示有理数和无理数;
C、数轴上的所有点表示的数全是实数;
D、有理数都能在数轴上表示出来,而数轴上的点表示的数不一定是有理数.第2课时 实数的性质与运算有理数和无理数统称实数.实数与数轴上的点是一一对应的相反数:只有符号不同的两个数叫做互为相反数
一般地,a和-a互为相反数.绝对值:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作:|a|
a与-a的绝对值相等,在数轴上对应的点关于原点对称.实数的性质有理数关于相反数和绝对值的意义同样适用于实数!例2、实数a,b在数轴上的位置如图所示,
化简|a+b|-|b-a|+a.3、已知实数a,b,c在数轴上的位置如图所示,化简:
|a+b|-|b+c|+|b-c|-|b|.实数的运算实数之间不仅可以进行加、减、乘、除(除数不为0)、乘方运算,而且正数和0可以进行开平方(偶次方)运算,任意一个实数可以进行开立方(奇次方)运算;
在进行实数的运算时,有理数的运算法则及运算性质同样适用.如果实数运算时,遇到无理数并且需要求出结果的近似值时,可以按照所要求的精确度用相应的近似有限小数去代替无理数(一般比精确度多一位小数),再进行计算. 实数的运算怎样进行?二、准确把握实数的性质三、掌握实数的运算四、实数在日常生活中的应用例6、学校有一个面积为100 m2的圆形花坛,为了需要,现将花坛的半径增加2 m,重建一个新的花坛.求新建花坛的半径.
