26.2 实际问题与反比例函数 课件(共20张PPT)2024-2025学年人教版数学九年级下册
文档属性
| 名称 | 26.2 实际问题与反比例函数 课件(共20张PPT)2024-2025学年人教版数学九年级下册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 22:36:23 | ||
图片预览






文档简介
(共20张PPT)
26.2 实际问题与反比例函数
第二十六章 反比例函数
古希腊科学家阿基米德曾说过:“给我一个支点,我可以把地球撬动。”
你认为这可能吗?为什么?
1.通过分析实际问题中两个变量之间的关系、建立函数模型的过程,进而解决问题.
2.体会数学与现实生活的联系,增强应用意识,提高运用代数方法解决问题的能力.
几位同学玩撬石头的游戏,已知阻力和阻力臂不变,分别是1200牛顿和0.5米,设动力为F,动力臂为L.回答下列问题:
(1)动力F与动力臂L有怎样的函数关系?
【分析】根据动力×动力臂=阻力×阻力臂
【解析】(1)由已知得F×L=1200×0.5
变形得:
例1
(2)当动力臂为1.5米时,撬动石头至少需要多大的力
当L=1.5时,
因此撬动石头至少需要400牛顿的力.
(3)若想使动力F不超过题(2)中所用力的一半,则动力臂至少要加长多少
根据(1)可知 FL=600
得函数解析式
因此,若想用力不超过400牛顿的一半,则动力臂至少要加长1.5米.
(4)小刚、小强、小健、小明分别选取了动力臂为1米、1.5米、2米、3米的撬棍,你能得出他们各自撬动石头至少需要多大的力吗?
从上述的运算中我们观察出什么规律?
【解析】
发现:动力臂越长,用的力越小.
即动力臂越长就越省力.
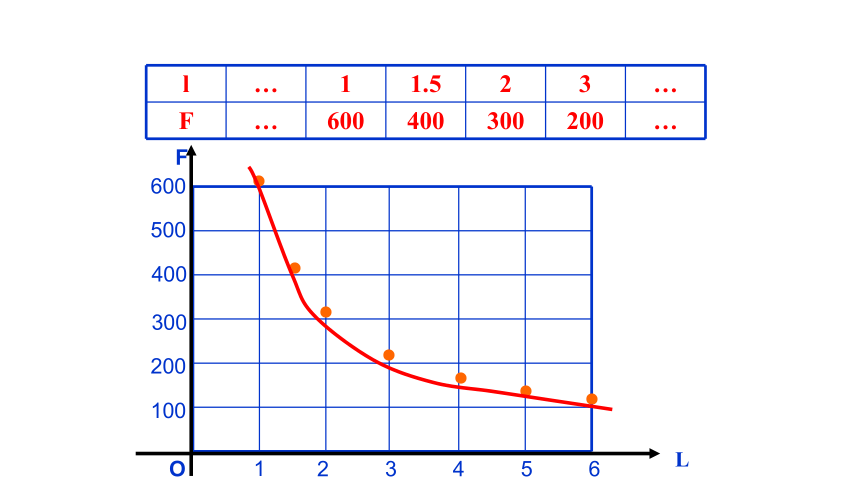
图象会在第三象限吗
你能画出图象吗
l … 1 1.5 2 3 …
F … 600 400 300 200 …
1
2
3
4
5
100
200
300
400
500
600
L
F
O
6
.
.
.
.
.
.
.
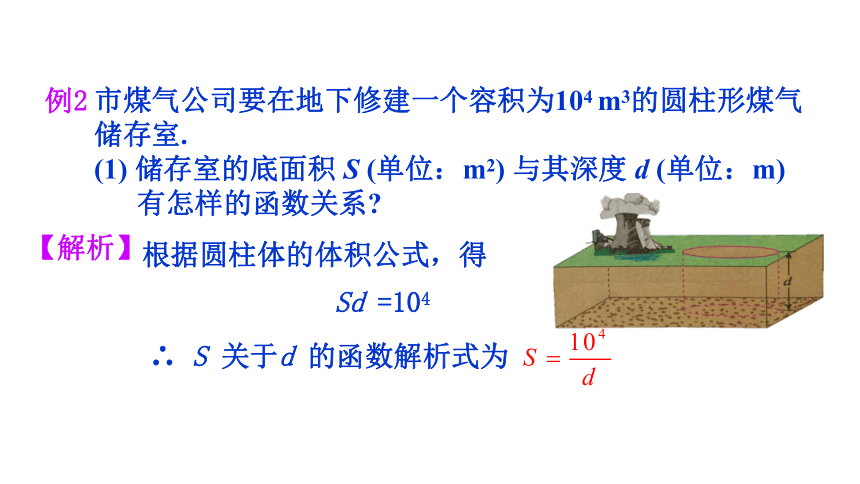
市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
(1) 储存室的底面积 S (单位:m2) 与其深度 d (单位:m)
有怎样的函数关系
根据圆柱体的体积公式,得
Sd =104
∴ S 关于d 的函数解析式为
例2
【解析】
(2) 公司决定把储存室的底面积 S 定为 500 m2,施工队施工时应该向下掘进多深
解得d = 20
如果把储存室的底面积定为 500 m ,施工时应向地下掘进 20 m 深.
把 S = 500 代入 ,得
【解析】
(3) 当施工队按 (2) 中的计划掘进到地下 15 m 时,公司临时改变计划,把储存室的深度改为 15 m. 相应地,储存室的底面积应改为多少 (结果保留小 数点后两位)
解得 S≈666.67
当储存室的深度为15 m 时,底面积应改为 666.67 m .
根据题意,把 d =15 代入 ,得
【解析】
第 (2) 问和第 (3) 问与过去所学的解分式方程和求代数式的值的问题有何联系?
第 (2) 问实际上是已知函数 S 的值,求自变量 d 的取值,第 (3) 问则是与第 (2) 问相反.
想一想:
1. 矩形面积为 6,它的长 y 与宽 x 之间的函数关系用图象可表示为( )
B
A.
B.
C.
D.
x
y
x
y
x
y
x
y
【跟踪训练】
2.如图,某玻璃器皿制造公司要制造一种容积为1升
(1升=1立方分米)的圆锥形漏斗.
漏斗口的面积 S (单位:dm2)与漏斗的深 d (单位:dm) 有怎样的函数关系
d
解:
(2) 如果漏斗的深为10cm,那么漏斗口的面积为多少dm2?
解:10cm=1dm,把 d =1 代入解析式,得
S =3
所以漏斗口的面积为 3 dm2.
(3) 如果漏斗口的面积为 60 cm2,则漏斗的深为多少
解:60 cm2 = 0.6 dm2
把 S =0.6 代入解析式,得
d =5.
所以漏斗的深为 5 dm.
实际问题中的反比例函数
过程:
分析实际情境→建立函数模型→明确数学问题
注意:
实际问题中的两个变量往往都只能取非负值;
作实际问题中的函数图象时,横、纵坐标的单
位长度不一定相同
设用电阻R表示电流I的函数解析式为I=K/R,
∵过(2,3),∴k=3×2=6,∴I=6/R 故选:D.
1.(2021 安乡县一模)已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A.
B.
C.
D.
【解析】
2.(2021 杭州二模)某气球内充满了一定量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示. (1)求这个函数的解析式; (2)当气体体积为1m3时,气压是多少? (3)当气球内的气压大于140kPa时,气球将
爆炸,为了安全起见,气体的体积应不小于多
少?(精确到0.01m3)
(1)设p=k/v,由题意知120=k/0.8 ∴k=96
故p=96/v
【解析】
(2)当v=1m3时,p=96/1=96(kPa)
(3)当p=140kPa时,v=96 140≈0.69(m3) ∴为了安全起见,气体的体积应不少于0.69m3.
奇迹是会发生的,但你得为之拼命地努力.
——佚名
26.2 实际问题与反比例函数
第二十六章 反比例函数
古希腊科学家阿基米德曾说过:“给我一个支点,我可以把地球撬动。”
你认为这可能吗?为什么?
1.通过分析实际问题中两个变量之间的关系、建立函数模型的过程,进而解决问题.
2.体会数学与现实生活的联系,增强应用意识,提高运用代数方法解决问题的能力.
几位同学玩撬石头的游戏,已知阻力和阻力臂不变,分别是1200牛顿和0.5米,设动力为F,动力臂为L.回答下列问题:
(1)动力F与动力臂L有怎样的函数关系?
【分析】根据动力×动力臂=阻力×阻力臂
【解析】(1)由已知得F×L=1200×0.5
变形得:
例1
(2)当动力臂为1.5米时,撬动石头至少需要多大的力
当L=1.5时,
因此撬动石头至少需要400牛顿的力.
(3)若想使动力F不超过题(2)中所用力的一半,则动力臂至少要加长多少
根据(1)可知 FL=600
得函数解析式
因此,若想用力不超过400牛顿的一半,则动力臂至少要加长1.5米.
(4)小刚、小强、小健、小明分别选取了动力臂为1米、1.5米、2米、3米的撬棍,你能得出他们各自撬动石头至少需要多大的力吗?
从上述的运算中我们观察出什么规律?
【解析】
发现:动力臂越长,用的力越小.
即动力臂越长就越省力.
图象会在第三象限吗
你能画出图象吗
l … 1 1.5 2 3 …
F … 600 400 300 200 …
1
2
3
4
5
100
200
300
400
500
600
L
F
O
6
.
.
.
.
.
.
.
市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
(1) 储存室的底面积 S (单位:m2) 与其深度 d (单位:m)
有怎样的函数关系
根据圆柱体的体积公式,得
Sd =104
∴ S 关于d 的函数解析式为
例2
【解析】
(2) 公司决定把储存室的底面积 S 定为 500 m2,施工队施工时应该向下掘进多深
解得d = 20
如果把储存室的底面积定为 500 m ,施工时应向地下掘进 20 m 深.
把 S = 500 代入 ,得
【解析】
(3) 当施工队按 (2) 中的计划掘进到地下 15 m 时,公司临时改变计划,把储存室的深度改为 15 m. 相应地,储存室的底面积应改为多少 (结果保留小 数点后两位)
解得 S≈666.67
当储存室的深度为15 m 时,底面积应改为 666.67 m .
根据题意,把 d =15 代入 ,得
【解析】
第 (2) 问和第 (3) 问与过去所学的解分式方程和求代数式的值的问题有何联系?
第 (2) 问实际上是已知函数 S 的值,求自变量 d 的取值,第 (3) 问则是与第 (2) 问相反.
想一想:
1. 矩形面积为 6,它的长 y 与宽 x 之间的函数关系用图象可表示为( )
B
A.
B.
C.
D.
x
y
x
y
x
y
x
y
【跟踪训练】
2.如图,某玻璃器皿制造公司要制造一种容积为1升
(1升=1立方分米)的圆锥形漏斗.
漏斗口的面积 S (单位:dm2)与漏斗的深 d (单位:dm) 有怎样的函数关系
d
解:
(2) 如果漏斗的深为10cm,那么漏斗口的面积为多少dm2?
解:10cm=1dm,把 d =1 代入解析式,得
S =3
所以漏斗口的面积为 3 dm2.
(3) 如果漏斗口的面积为 60 cm2,则漏斗的深为多少
解:60 cm2 = 0.6 dm2
把 S =0.6 代入解析式,得
d =5.
所以漏斗的深为 5 dm.
实际问题中的反比例函数
过程:
分析实际情境→建立函数模型→明确数学问题
注意:
实际问题中的两个变量往往都只能取非负值;
作实际问题中的函数图象时,横、纵坐标的单
位长度不一定相同
设用电阻R表示电流I的函数解析式为I=K/R,
∵过(2,3),∴k=3×2=6,∴I=6/R 故选:D.
1.(2021 安乡县一模)已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A.
B.
C.
D.
【解析】
2.(2021 杭州二模)某气球内充满了一定量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示. (1)求这个函数的解析式; (2)当气体体积为1m3时,气压是多少? (3)当气球内的气压大于140kPa时,气球将
爆炸,为了安全起见,气体的体积应不小于多
少?(精确到0.01m3)
(1)设p=k/v,由题意知120=k/0.8 ∴k=96
故p=96/v
【解析】
(2)当v=1m3时,p=96/1=96(kPa)
(3)当p=140kPa时,v=96 140≈0.69(m3) ∴为了安全起见,气体的体积应不少于0.69m3.
奇迹是会发生的,但你得为之拼命地努力.
——佚名
