27.2.1 相似三角形的判定 第1课时 课件(共23张PPT) 2024-2025学年人教版数学九年级下册
文档属性
| 名称 | 27.2.1 相似三角形的判定 第1课时 课件(共23张PPT) 2024-2025学年人教版数学九年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 741.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 21:10:43 | ||
图片预览




文档简介
(共23张PPT)
27.2.1 相似三角形的判定
第1课时
27.2 相似三角形
第二十七章 相 似
1.什么叫做相似多边形?
对应角相等、对应边成比例的两个多边形叫做相似多边形.
2.相似多边形的性质和判定各是什么?
相似多边形
性质
判定
对应角相等
对应边成比例
3.什么叫做相似比?
相似多边形对应边的比叫做相似比,用字母k表示.
1.理解相似三角形的概念.
2.理解平行线分线段成比例的基本事实及其推论,掌握相似三角形判定定理的预备定理的有关证明. (重点、难点)
3.掌握平行线分线段成比例的基本事实及其推论的应用,会用平行线判定两个三角形相似并进行证明和计算.
(重点、难点)
A
B
C
A′
B ′
C ′
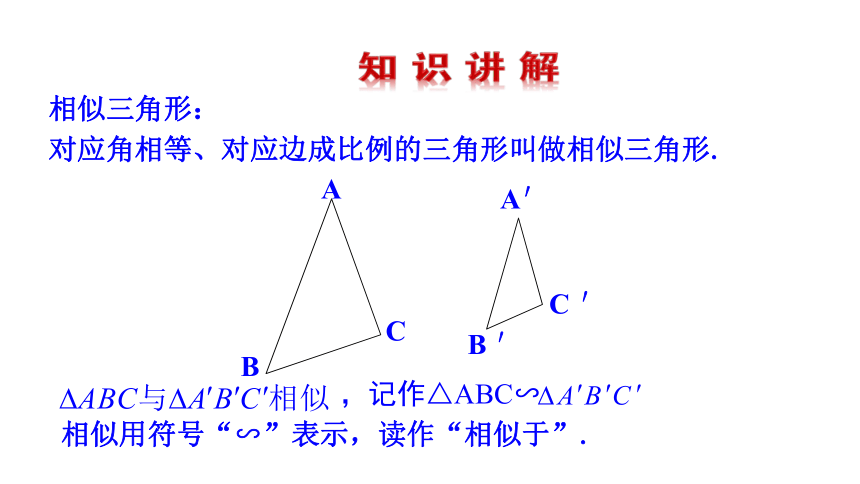
相似三角形:
对应角相等、对应边成比例的三角形叫做相似三角形.
相似用符号“∽”表示,读作“相似于”.
,记作△ABC∽
如图,在△ABC与△A′B′C′中,∵ △ABC∽△A′B′C′
A
B
C
A′
B′
C′
定义,即是性质,也是判定,你能用几何语言表述相似三角形性质吗?
∴
其中k是相似比,即△ABC与△A′B′C′的相似比是k, △A′B′C′与△ABC的相似比是 .
注意:通常要把表示对应角顶点的字母写在对应的位置上.
A
B
C
A′
B′
C′
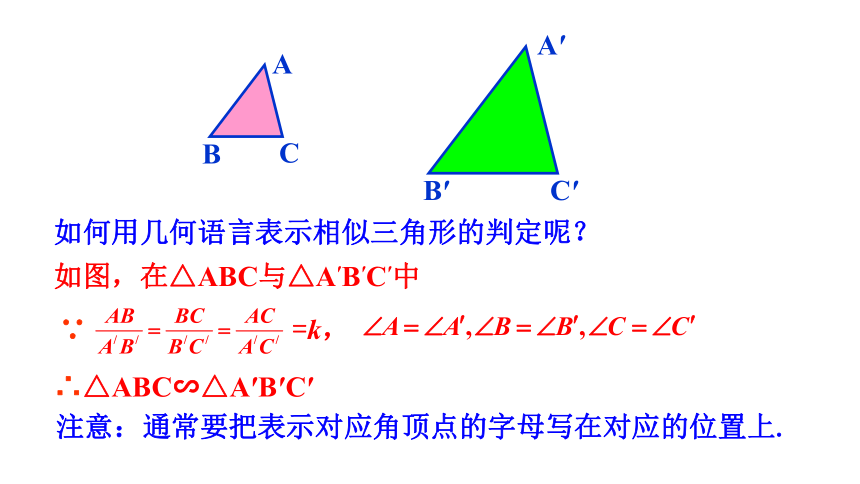
如何用几何语言表示相似三角形的判定呢?
如图,在△ABC与△A′B′C′中
=k,
∵
∴△ABC∽△A′B′C′
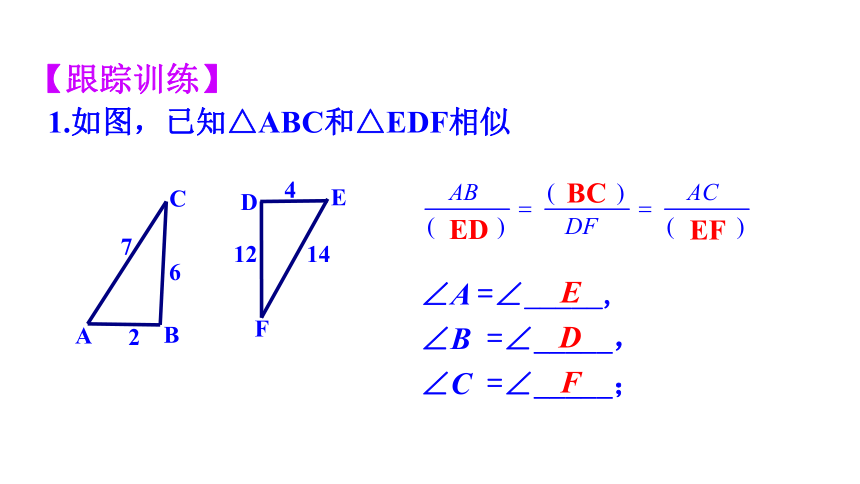
【跟踪训练】
E
F
D
C
B
A
7
6
2
12
14
4
∠A =∠_____,
∠B =∠_____,
∠C =∠_____;
E
D
F
1.如图,已知△ABC和△EDF相似
ED
BC
EF
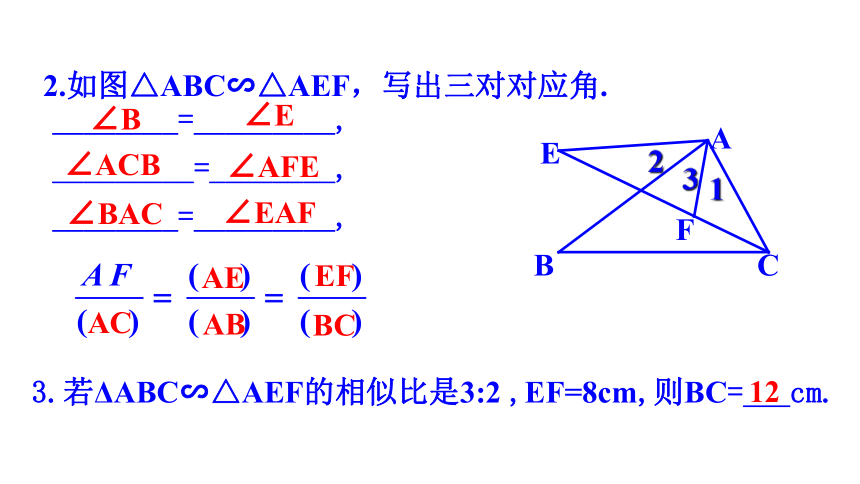
2.如图△ABC∽△AEF,写出三对对应角.
________=_________,
_________=________,
________=_________,
3.若ΔABC∽△AEF的相似比是3:2 ,EF=8cm,则BC= cm.
F
E
C
B
A
1
2
3
AC
AE
AB
EF
BC
∠B
∠E
∠ACB
∠AFE
∠BAC
∠EAF
12
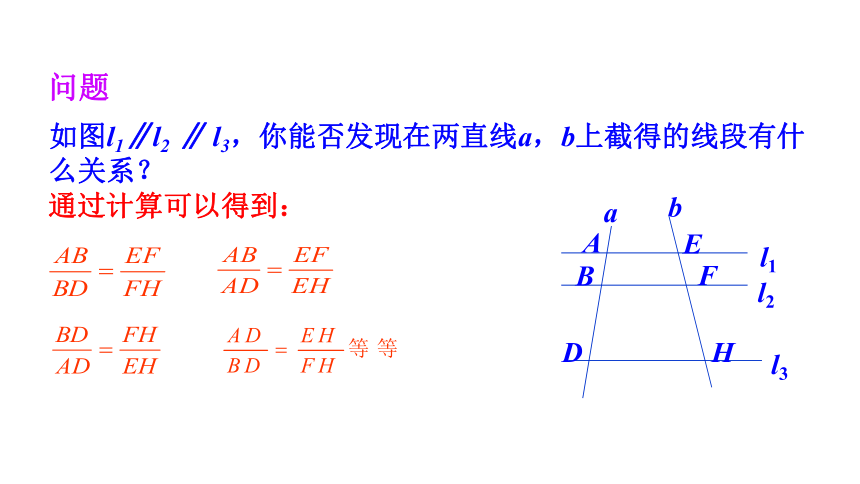
如图l1∥l2 ∥ l3,你能否发现在两直线a,b上截得的线段有什么关系?
l3
l1
l2
A
B
D
E
F
H
a
b
通过计算可以得到:
问题
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例.
说明: ①定理的条件是“两条直线被一组平行线所截”.
②是“对应线段成比例”,注意“对应”两字.
强化“对应”两字的理解和记忆,如图:
l3
l1
l2
A
B
D
E
F
H
a
b
由此可以得到:
如图l1∥l2∥l3,试根据图形写出成比例线段.
l3
a
b
l1
l2
A
B
C
D
E
F
l2
l3
l1
l3
l
l
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l
推论:
l2
如图,DE∥BC,△ADE与△ABC有什么关系 说明理由.
相似.
A
B
C
D
E
在△ADE与△ABC中,∠A= ∠A
∵ DE∥BC
∴∠ADE=∠B,∠AED=∠C,
过E作EF∥AB交BC于F,
∵四边形DBFE是平行四边形,
F
∴DE=BF
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
∴△ADE∽△ABC
探究
【证明】
定理:
平行于三角形一边的直线与其他两边(或延长线)相交,所
得的三角形与原三角形________.
相似
“A”型
“X”型
D
E
O
B
C
A
B
C
D
E
1. 如图,在 △ABC中,DE∥BC,则△______ ∽△______,
对应边的比例式为 = =
ADE
ABC
——
——.
B
C
A
D
E
【跟踪训练】
2.如图,已知:△ABC中,DE∥BC,AD=3,DB=6,AE=2,则EC的长.
【解析】C
∵△ABC中,DE∥BC
∵AD=3,DB=6,AE=2
∴EC=4
三个角对应相等 ,三条边对应成比例的两个三角形,叫做相似三角形.
△ABC与△DEF相似,记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上!
相似三角形的各对应角相等,各对应边对应成比例.
相似比就是它们的对应边的比.
一、平行线分线段成比例定理:
三条平行线截两条直线,所得的对应线段成比例. (关键要能熟练地找出对应线段)
二、平行线分线段成比例定理的推论:
平行于三角形一边的直线截其他两边,所得的对应线段成比例.
(关键要能熟练地找出对应线段)
四、注意该定理在三角形中的应用:
三、要熟悉该定理的几种基本图形:
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
1. 如图,△ABC∽△DEF,相似比为1:2,若 BC=1,则 EF 的
长为 ( )
A. 1 B. 2
C. 3 D. 4
B
C
A
E
F
D
B
2. 如图,在 △ABC 中,EF∥BC,AE=2cm,BE=6cm,
BC = 4 cm,EF 长为( )
A
A. 1cm B. cm
C. 3cm D. 2cm
A
B
C
E
F
3. 如图,已知菱形 ABCD 内接于△AEF,AE=5cm, AF = 4 cm,
求菱形的边长.
∵ 四边形 ABCD 为菱形
B
C
A
D
E
F
∴CD∥AB
∴
设菱形的边长为 x cm,则CD= AD = x cm,
DF = (4-x) cm
∴ 解得 x =
∴菱形的边长为 cm.
【解析】
本来无望的事,大胆尝试,往往能成功.
——莎士比亚
27.2.1 相似三角形的判定
第1课时
27.2 相似三角形
第二十七章 相 似
1.什么叫做相似多边形?
对应角相等、对应边成比例的两个多边形叫做相似多边形.
2.相似多边形的性质和判定各是什么?
相似多边形
性质
判定
对应角相等
对应边成比例
3.什么叫做相似比?
相似多边形对应边的比叫做相似比,用字母k表示.
1.理解相似三角形的概念.
2.理解平行线分线段成比例的基本事实及其推论,掌握相似三角形判定定理的预备定理的有关证明. (重点、难点)
3.掌握平行线分线段成比例的基本事实及其推论的应用,会用平行线判定两个三角形相似并进行证明和计算.
(重点、难点)
A
B
C
A′
B ′
C ′
相似三角形:
对应角相等、对应边成比例的三角形叫做相似三角形.
相似用符号“∽”表示,读作“相似于”.
,记作△ABC∽
如图,在△ABC与△A′B′C′中,∵ △ABC∽△A′B′C′
A
B
C
A′
B′
C′
定义,即是性质,也是判定,你能用几何语言表述相似三角形性质吗?
∴
其中k是相似比,即△ABC与△A′B′C′的相似比是k, △A′B′C′与△ABC的相似比是 .
注意:通常要把表示对应角顶点的字母写在对应的位置上.
A
B
C
A′
B′
C′
如何用几何语言表示相似三角形的判定呢?
如图,在△ABC与△A′B′C′中
=k,
∵
∴△ABC∽△A′B′C′
【跟踪训练】
E
F
D
C
B
A
7
6
2
12
14
4
∠A =∠_____,
∠B =∠_____,
∠C =∠_____;
E
D
F
1.如图,已知△ABC和△EDF相似
ED
BC
EF
2.如图△ABC∽△AEF,写出三对对应角.
________=_________,
_________=________,
________=_________,
3.若ΔABC∽△AEF的相似比是3:2 ,EF=8cm,则BC= cm.
F
E
C
B
A
1
2
3
AC
AE
AB
EF
BC
∠B
∠E
∠ACB
∠AFE
∠BAC
∠EAF
12
如图l1∥l2 ∥ l3,你能否发现在两直线a,b上截得的线段有什么关系?
l3
l1
l2
A
B
D
E
F
H
a
b
通过计算可以得到:
问题
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例.
说明: ①定理的条件是“两条直线被一组平行线所截”.
②是“对应线段成比例”,注意“对应”两字.
强化“对应”两字的理解和记忆,如图:
l3
l1
l2
A
B
D
E
F
H
a
b
由此可以得到:
如图l1∥l2∥l3,试根据图形写出成比例线段.
l3
a
b
l1
l2
A
B
C
D
E
F
l2
l3
l1
l3
l
l
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l
推论:
l2
如图,DE∥BC,△ADE与△ABC有什么关系 说明理由.
相似.
A
B
C
D
E
在△ADE与△ABC中,∠A= ∠A
∵ DE∥BC
∴∠ADE=∠B,∠AED=∠C,
过E作EF∥AB交BC于F,
∵四边形DBFE是平行四边形,
F
∴DE=BF
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
∴△ADE∽△ABC
探究
【证明】
定理:
平行于三角形一边的直线与其他两边(或延长线)相交,所
得的三角形与原三角形________.
相似
“A”型
“X”型
D
E
O
B
C
A
B
C
D
E
1. 如图,在 △ABC中,DE∥BC,则△______ ∽△______,
对应边的比例式为 = =
ADE
ABC
——
——.
B
C
A
D
E
【跟踪训练】
2.如图,已知:△ABC中,DE∥BC,AD=3,DB=6,AE=2,则EC的长.
【解析】C
∵△ABC中,DE∥BC
∵AD=3,DB=6,AE=2
∴EC=4
三个角对应相等 ,三条边对应成比例的两个三角形,叫做相似三角形.
△ABC与△DEF相似,记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上!
相似三角形的各对应角相等,各对应边对应成比例.
相似比就是它们的对应边的比.
一、平行线分线段成比例定理:
三条平行线截两条直线,所得的对应线段成比例. (关键要能熟练地找出对应线段)
二、平行线分线段成比例定理的推论:
平行于三角形一边的直线截其他两边,所得的对应线段成比例.
(关键要能熟练地找出对应线段)
四、注意该定理在三角形中的应用:
三、要熟悉该定理的几种基本图形:
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
1. 如图,△ABC∽△DEF,相似比为1:2,若 BC=1,则 EF 的
长为 ( )
A. 1 B. 2
C. 3 D. 4
B
C
A
E
F
D
B
2. 如图,在 △ABC 中,EF∥BC,AE=2cm,BE=6cm,
BC = 4 cm,EF 长为( )
A
A. 1cm B. cm
C. 3cm D. 2cm
A
B
C
E
F
3. 如图,已知菱形 ABCD 内接于△AEF,AE=5cm, AF = 4 cm,
求菱形的边长.
∵ 四边形 ABCD 为菱形
B
C
A
D
E
F
∴CD∥AB
∴
设菱形的边长为 x cm,则CD= AD = x cm,
DF = (4-x) cm
∴ 解得 x =
∴菱形的边长为 cm.
【解析】
本来无望的事,大胆尝试,往往能成功.
——莎士比亚
