27.2.1 相似三角形的判定 第3课时 课件(共20张PPT)2024-2025学年人教版数学九年级下册
文档属性
| 名称 | 27.2.1 相似三角形的判定 第3课时 课件(共20张PPT)2024-2025学年人教版数学九年级下册 |  | |
| 格式 | ppt | ||
| 文件大小 | 724.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 22:44:32 | ||
图片预览




文档简介
(共20张PPT)
27.2.1 相似三角形的判定
第3课时
27.2 相似三角形
第二十七章 相 似
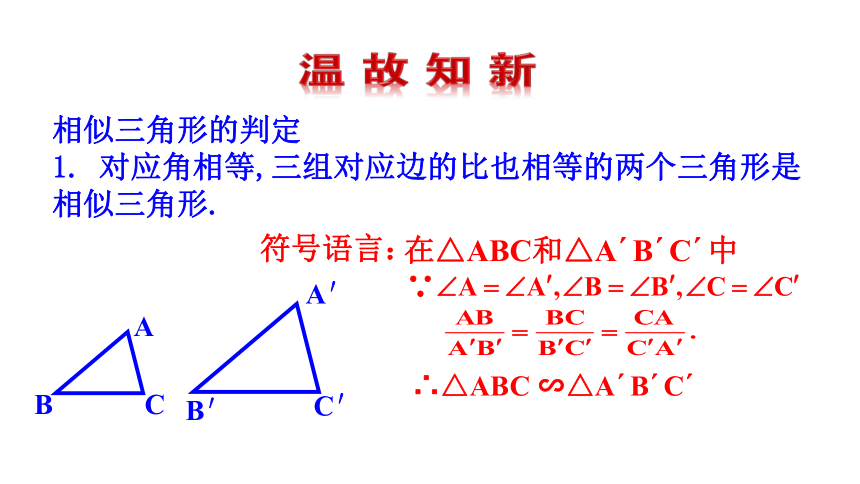
1. 对应角相等,三组对应边的比也相等的两个三角形是相似三角形.
相似三角形的判定
A
C′
B′
A′
C
B
∴△ABC ∽△A B C
∵
符号语言:
在△ABC和△A B C 中
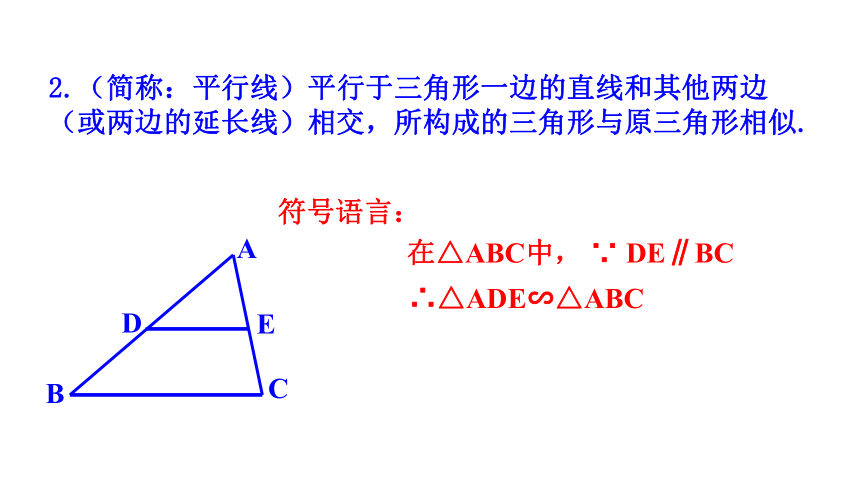
2.(简称:平行线)平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
D
A
B
C
E
在△ABC中, ∵ DE∥BC
∴△ADE∽△ABC
符号语言:
3.(简称:三边)如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
符号语言:
∴△A B C ∽△ABC
∵
在△A B C 和△ABC中,
A
C′
B′
A′
C
B
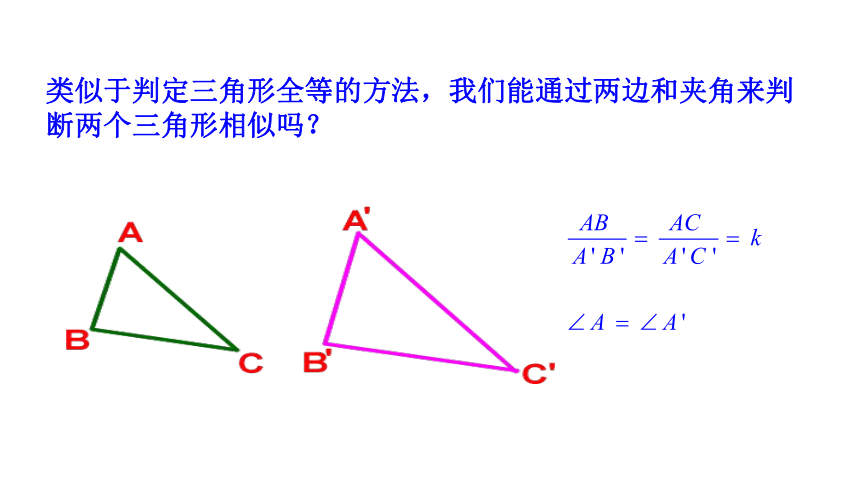
类似于判定三角形全等的方法,我们能通过两边和夹角来判断两个三角形相似吗?
1. 探索“两边成比例且夹角相等的两个角形相似”的判定定理.
2. 会根据边和角的关系来判定两个三角形相似,并进行相关计算. (重点、难点)
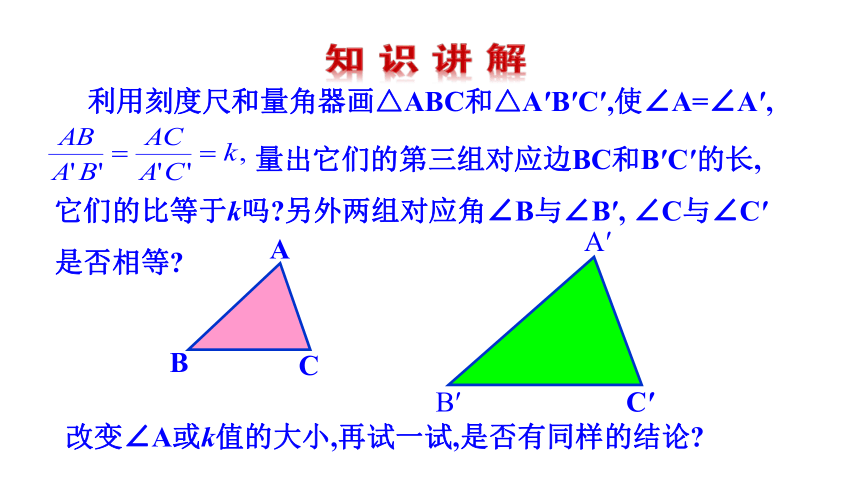
利用刻度尺和量角器画△ABC和△A′B′C′,使∠A=∠A′,
量出它们的第三组对应边BC和B′C′的长,
它们的比等于k吗 另外两组对应角∠B与∠B′, ∠C与∠C′
是否相等
A
B
C
A′
B′
C′
改变∠A或k值的大小,再试一试,是否有同样的结论
如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE∽△ABC呢?
所画如图所示,此时,
如果两个三角形的两组对应边的比相等,并且相应的夹角相等.那么这两个三角形一定相似吗?
A′
B′
C′
A
B
C
E
D
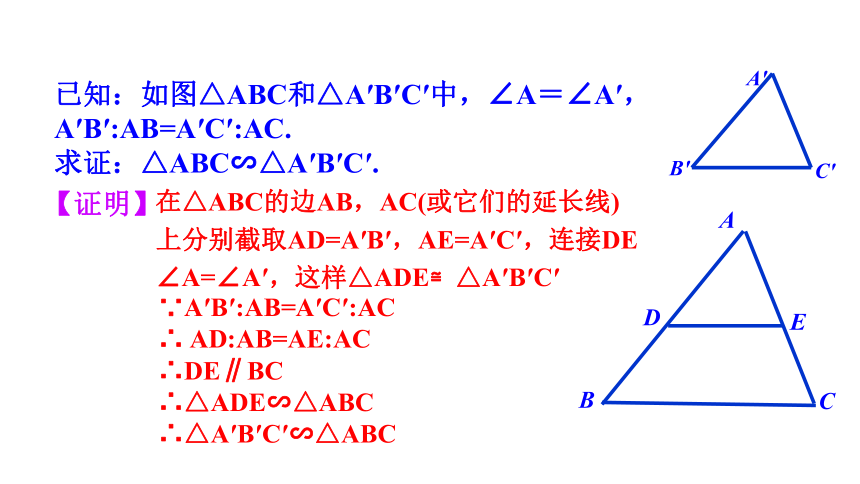
在△ABC的边AB,AC(或它们的延长线)
上分别截取AD=A′B′,AE=A′C′,连接DE
∠A=∠A′,这样△ADE≌△A′B′C′
∵A′B′:AB=A′C′:AC
∴ AD:AB=AE:AC
∴DE∥BC
∴△ADE∽△ABC
∴△A′B′C′∽△ABC
已知:如图△ABC和△A′B′C′中,∠A=∠A′,A′B′:AB=A′C′:AC.
求证:△ABC∽△A′B′C′.
【证明】
∴△ABC∽△A′B′C′
两边成比例且夹角相等的两个三角形相似.
A
B
C
A′
B′
C′
想一想:如果对应相等的角不是两组对应边的夹角,那么两个三角形是否相似呢?
3.2
3.2
G
C
50°
)
4
A
B
2
1.6
50°
)
E
D
F
结论:
如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角.
根据下列条件,判断 △ABC 和 △A′B′C′ 是否相似,并说明理由:
∠A=120°,AB=7 cm,AC=14 cm, ∠A′=120°,A′B′=3 cm ,A′C′=6 cm.
又 ∠A′ = ∠A
∴ △ABC ∽ △A′B′C′
【例题】
【证明】
在 △ABC 和 △DEF 中,∠C =∠F=70°,AC =3.5 cm,
BC = 2.5 cm,DF =2.1 cm,EF =1.5 cm.
求证:△DEF∽△ABC.
A
C
B
F
E
D
∵ AC = 3.5 cm,BC = 2.5 cm,
DF = 2.1 cm,EF = 1.5 cm
又 ∵∠C =∠F = 70°
∴ △DEF ∽△ABC
【跟踪训练】
【证明】
1. 平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
2. 三边对应成比例的两个三角形相似.
3. 两边成比例且夹角相等的两个三角形相似.
相似三角形的判定方法:
1. 如图 △AEB 和 △FEC (填 “相似” 或 “不相似”) .
54
30
36
45
E
A
F
C
B
1
2
相似
2. 判断
(1) 两个等边三角形相似 ( )
(2) 两个直角三角形相似 ( )
(3) 两个等腰直角三角形相似 ( )
(4) 有一个角是50°的两个等腰三角形相似 ( )
×
√
√
×
∵ AE=1.5,AC=2
3.如图,D,E分别是 △ABC 的边 AC,AB 上的点,AE=1.5,AC=2,BC=3,且 ,求 DE 的长.
A
C
B
E
D
又∵∠EAD=∠CAB
∴ △ADE ∽△ABC
提示:解题时要找准对应边.
【解析】
4. 如图,在四边形 ABCD 中,已知 ∠B =∠ACD, AB=6,BC=4,AC=5,CD= ,求 AD 的长.
A
B
C
D
∵AB=6,BC=4,AC=5,CD= ,
又∵∠B=∠ACD
∴ △ABC ∽ △DCA
【解析】
知识是一种快乐,而好奇则是知识的萌芽.
——培根
27.2.1 相似三角形的判定
第3课时
27.2 相似三角形
第二十七章 相 似
1. 对应角相等,三组对应边的比也相等的两个三角形是相似三角形.
相似三角形的判定
A
C′
B′
A′
C
B
∴△ABC ∽△A B C
∵
符号语言:
在△ABC和△A B C 中
2.(简称:平行线)平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
D
A
B
C
E
在△ABC中, ∵ DE∥BC
∴△ADE∽△ABC
符号语言:
3.(简称:三边)如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
符号语言:
∴△A B C ∽△ABC
∵
在△A B C 和△ABC中,
A
C′
B′
A′
C
B
类似于判定三角形全等的方法,我们能通过两边和夹角来判断两个三角形相似吗?
1. 探索“两边成比例且夹角相等的两个角形相似”的判定定理.
2. 会根据边和角的关系来判定两个三角形相似,并进行相关计算. (重点、难点)
利用刻度尺和量角器画△ABC和△A′B′C′,使∠A=∠A′,
量出它们的第三组对应边BC和B′C′的长,
它们的比等于k吗 另外两组对应角∠B与∠B′, ∠C与∠C′
是否相等
A
B
C
A′
B′
C′
改变∠A或k值的大小,再试一试,是否有同样的结论
如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE∽△ABC呢?
所画如图所示,此时,
如果两个三角形的两组对应边的比相等,并且相应的夹角相等.那么这两个三角形一定相似吗?
A′
B′
C′
A
B
C
E
D
在△ABC的边AB,AC(或它们的延长线)
上分别截取AD=A′B′,AE=A′C′,连接DE
∠A=∠A′,这样△ADE≌△A′B′C′
∵A′B′:AB=A′C′:AC
∴ AD:AB=AE:AC
∴DE∥BC
∴△ADE∽△ABC
∴△A′B′C′∽△ABC
已知:如图△ABC和△A′B′C′中,∠A=∠A′,A′B′:AB=A′C′:AC.
求证:△ABC∽△A′B′C′.
【证明】
∴△ABC∽△A′B′C′
两边成比例且夹角相等的两个三角形相似.
A
B
C
A′
B′
C′
想一想:如果对应相等的角不是两组对应边的夹角,那么两个三角形是否相似呢?
3.2
3.2
G
C
50°
)
4
A
B
2
1.6
50°
)
E
D
F
结论:
如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角.
根据下列条件,判断 △ABC 和 △A′B′C′ 是否相似,并说明理由:
∠A=120°,AB=7 cm,AC=14 cm, ∠A′=120°,A′B′=3 cm ,A′C′=6 cm.
又 ∠A′ = ∠A
∴ △ABC ∽ △A′B′C′
【例题】
【证明】
在 △ABC 和 △DEF 中,∠C =∠F=70°,AC =3.5 cm,
BC = 2.5 cm,DF =2.1 cm,EF =1.5 cm.
求证:△DEF∽△ABC.
A
C
B
F
E
D
∵ AC = 3.5 cm,BC = 2.5 cm,
DF = 2.1 cm,EF = 1.5 cm
又 ∵∠C =∠F = 70°
∴ △DEF ∽△ABC
【跟踪训练】
【证明】
1. 平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
2. 三边对应成比例的两个三角形相似.
3. 两边成比例且夹角相等的两个三角形相似.
相似三角形的判定方法:
1. 如图 △AEB 和 △FEC (填 “相似” 或 “不相似”) .
54
30
36
45
E
A
F
C
B
1
2
相似
2. 判断
(1) 两个等边三角形相似 ( )
(2) 两个直角三角形相似 ( )
(3) 两个等腰直角三角形相似 ( )
(4) 有一个角是50°的两个等腰三角形相似 ( )
×
√
√
×
∵ AE=1.5,AC=2
3.如图,D,E分别是 △ABC 的边 AC,AB 上的点,AE=1.5,AC=2,BC=3,且 ,求 DE 的长.
A
C
B
E
D
又∵∠EAD=∠CAB
∴ △ADE ∽△ABC
提示:解题时要找准对应边.
【解析】
4. 如图,在四边形 ABCD 中,已知 ∠B =∠ACD, AB=6,BC=4,AC=5,CD= ,求 AD 的长.
A
B
C
D
∵AB=6,BC=4,AC=5,CD= ,
又∵∠B=∠ACD
∴ △ABC ∽ △DCA
【解析】
知识是一种快乐,而好奇则是知识的萌芽.
——培根
