27.3 位似 第1课时 课件(共21张PPT)2024-2025学年人教版数学九年级下册
文档属性
| 名称 | 27.3 位似 第1课时 课件(共21张PPT)2024-2025学年人教版数学九年级下册 |  | |
| 格式 | ppt | ||
| 文件大小 | 556.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 22:55:05 | ||
图片预览




文档简介
(共21张PPT)
第1课时
27.3 位似
第二十七章 相 似
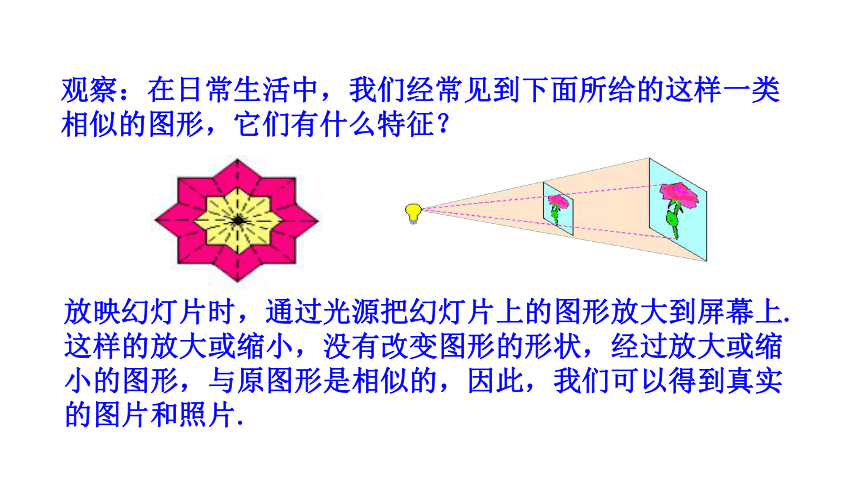
观察:在日常生活中,我们经常见到下面所给的这样一类相似的图形,它们有什么特征?
放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上.这样的放大或缩小,没有改变图形的形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和照片.
1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质.
2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.
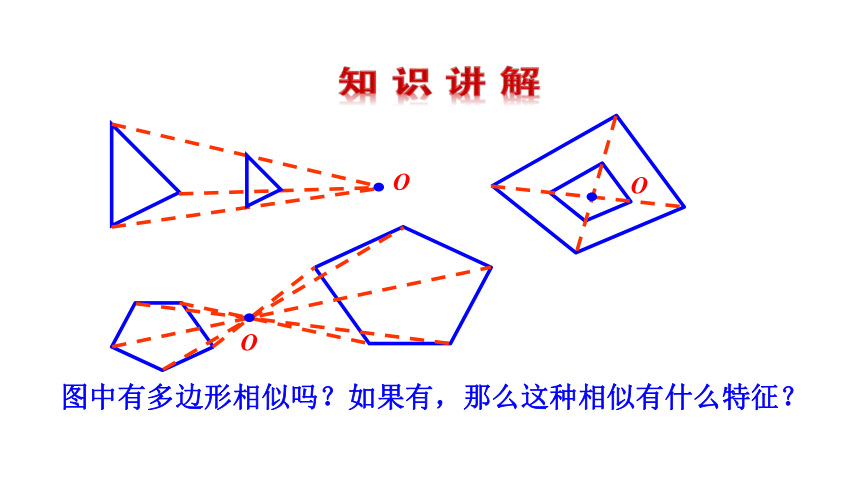
图中有多边形相似吗?如果有,那么这种相似有什么特征?
O
O
O
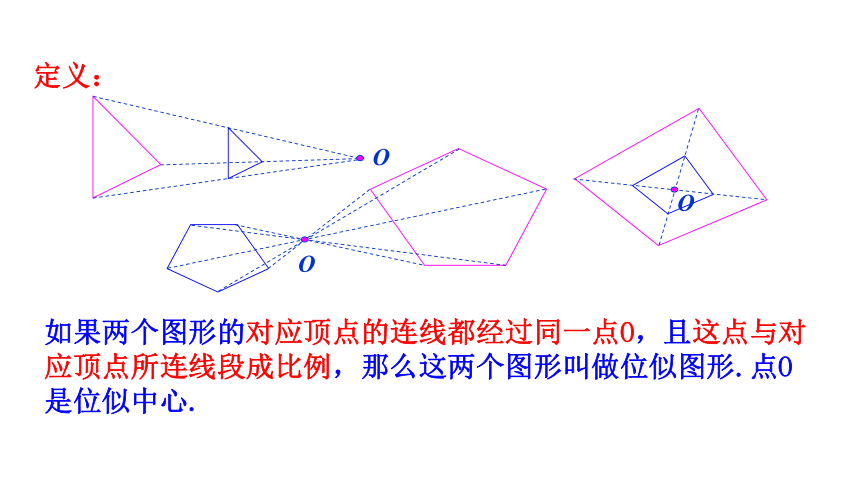
如果两个图形的对应顶点的连线都经过同一点O,且这点与对应顶点所连线段成比例,那么这两个图形叫做位似图形.点O是位似中心.
定义:
O
O
O
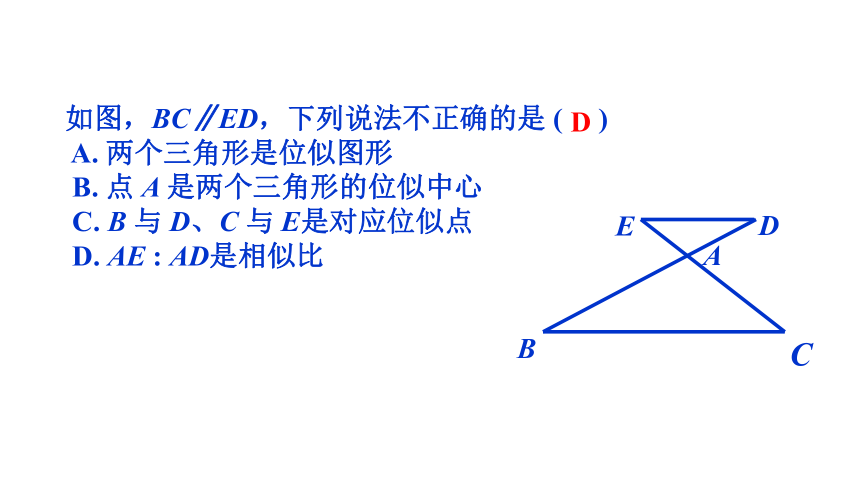
如图,BC∥ED,下列说法不正确的是 ( )
A. 两个三角形是位似图形
B. 点 A 是两个三角形的位似中心
C. B 与 D、C 与 E是对应位似点
D. AE : AD是相似比
D
D
E
A
B
C
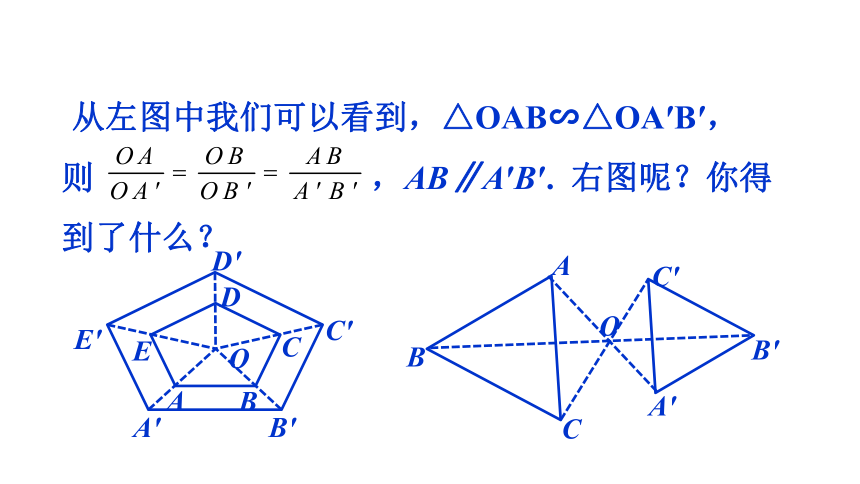
从左图中我们可以看到,△OAB∽△OA′B′,
则 ,AB∥A′B′. 右图呢?你得到了什么?
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
1. 位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等.
2. 位似图形上任意一对对应点到位似中心的距离之比等于相似比.(位似图形的相似比也叫做位似比)
3. 对应线段平行或者在一条直线上.
归纳:
(3) 顺次连接点 A' 、B' 、C' 、D' ,所得四边形 A' B ' C' D' 就是所要求的图形.
O
D
A
B
C
A'
B'
C'
D'
例 把四边形 ABCD 缩小到原来的 1/2.
(1) 在四边形外任选一点 O (如图);
(2) 分别在线段 OA、OB、OC、OD 上取点 A‘ 、B’ 、C' 、D' ,使得 ;
利用位似,可以将一个图形放大或缩小
思考:
对于上面的问题,还有其他方法吗?如果在四边形外任
选一个点 O,分别在 OA、OB、OC、OD 的反向延长线上取
A′ 、B′ 、C′、D′,使得
呢?如果点 O 取在四边形 ABCD 内部呢?分别画出这时得到
的图形.
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
A'
B'
C'
D'
O
A
B
C
F
●
E
●
D
●
选择以上一种方法将△ABC的三边缩小为原来的 .
如图,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F;顺次连接EF,FD,DE,△DEF的三边就是△ABC相应三边的 .实际上△ABC与△DEF是位似图形.
【跟踪训练】
【解析】
A
B
C
D
选出下面不同于其他三组的图形 ( )
B
O
.
A
B
C
A1
C1
B1
1.所有对应顶点的连线都交于同一点——位似中心
2.位似中心与对应顶点所连线段成比例
一、位似图形的定义
C
B
B’
C’
A
O
.
二、位似图形的结论
结论1:位似图形是相似图形的特殊情形,位似图形是相似图形,反之不成立.
∠AED=∠B
C
O
A
B
A′
C′
B′
结论2:位似中心的位置由两个图形的位置决定,可能在两个图形的同侧、异侧,图形的内部、边上或顶点上.
1. 如图,△ABC与△DEF是位似图形,位似比为 2 : 3,已知 AB=4,则 DE 的长为_____.
6
2. 如图,以 O 为位似中心,将 △ABC 放大为原来的 2倍.
O
A
B
C
①作射线OA 、OB 、 OC;
②分别在OA、OB 、OC 上取点
A' 、B' 、C' 使得
③顺次连接 A' 、B' 、C' 就是所要求的图形.
A'
B'
C'
3. 如图,正五边形 FGHMN 与正五边形 ABCDE 是位似图形,若AB : FG = 2 : 3,则下列结论正确的是( )
A. 2 DE = 3 MN B. 3 DE = 2 MN
C. 3∠A = 2∠F D. 2∠A = 3∠F
B
A
B
E
C
D
N
F
G
H
M
4. 下列说法:
①位似图形一定是相似图形;
②相似图形一定是位似图形;
③两个位似图形若全等,则位似中心在两个图形之间;
④若五边形ABCDE与五边形A′B′C′D′E′位似;
则其中 △ABC 与 △A′B′C′ 也是位似的,且位似比相等.
其中正确的有 .
①④
从来没有人读书,只有人在书中读自己,发现自己或检查自己.
——罗曼·罗兰
第1课时
27.3 位似
第二十七章 相 似
观察:在日常生活中,我们经常见到下面所给的这样一类相似的图形,它们有什么特征?
放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上.这样的放大或缩小,没有改变图形的形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和照片.
1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质.
2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.
图中有多边形相似吗?如果有,那么这种相似有什么特征?
O
O
O
如果两个图形的对应顶点的连线都经过同一点O,且这点与对应顶点所连线段成比例,那么这两个图形叫做位似图形.点O是位似中心.
定义:
O
O
O
如图,BC∥ED,下列说法不正确的是 ( )
A. 两个三角形是位似图形
B. 点 A 是两个三角形的位似中心
C. B 与 D、C 与 E是对应位似点
D. AE : AD是相似比
D
D
E
A
B
C
从左图中我们可以看到,△OAB∽△OA′B′,
则 ,AB∥A′B′. 右图呢?你得到了什么?
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
1. 位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等.
2. 位似图形上任意一对对应点到位似中心的距离之比等于相似比.(位似图形的相似比也叫做位似比)
3. 对应线段平行或者在一条直线上.
归纳:
(3) 顺次连接点 A' 、B' 、C' 、D' ,所得四边形 A' B ' C' D' 就是所要求的图形.
O
D
A
B
C
A'
B'
C'
D'
例 把四边形 ABCD 缩小到原来的 1/2.
(1) 在四边形外任选一点 O (如图);
(2) 分别在线段 OA、OB、OC、OD 上取点 A‘ 、B’ 、C' 、D' ,使得 ;
利用位似,可以将一个图形放大或缩小
思考:
对于上面的问题,还有其他方法吗?如果在四边形外任
选一个点 O,分别在 OA、OB、OC、OD 的反向延长线上取
A′ 、B′ 、C′、D′,使得
呢?如果点 O 取在四边形 ABCD 内部呢?分别画出这时得到
的图形.
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
A'
B'
C'
D'
O
A
B
C
F
●
E
●
D
●
选择以上一种方法将△ABC的三边缩小为原来的 .
如图,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F;顺次连接EF,FD,DE,△DEF的三边就是△ABC相应三边的 .实际上△ABC与△DEF是位似图形.
【跟踪训练】
【解析】
A
B
C
D
选出下面不同于其他三组的图形 ( )
B
O
.
A
B
C
A1
C1
B1
1.所有对应顶点的连线都交于同一点——位似中心
2.位似中心与对应顶点所连线段成比例
一、位似图形的定义
C
B
B’
C’
A
O
.
二、位似图形的结论
结论1:位似图形是相似图形的特殊情形,位似图形是相似图形,反之不成立.
∠AED=∠B
C
O
A
B
A′
C′
B′
结论2:位似中心的位置由两个图形的位置决定,可能在两个图形的同侧、异侧,图形的内部、边上或顶点上.
1. 如图,△ABC与△DEF是位似图形,位似比为 2 : 3,已知 AB=4,则 DE 的长为_____.
6
2. 如图,以 O 为位似中心,将 △ABC 放大为原来的 2倍.
O
A
B
C
①作射线OA 、OB 、 OC;
②分别在OA、OB 、OC 上取点
A' 、B' 、C' 使得
③顺次连接 A' 、B' 、C' 就是所要求的图形.
A'
B'
C'
3. 如图,正五边形 FGHMN 与正五边形 ABCDE 是位似图形,若AB : FG = 2 : 3,则下列结论正确的是( )
A. 2 DE = 3 MN B. 3 DE = 2 MN
C. 3∠A = 2∠F D. 2∠A = 3∠F
B
A
B
E
C
D
N
F
G
H
M
4. 下列说法:
①位似图形一定是相似图形;
②相似图形一定是位似图形;
③两个位似图形若全等,则位似中心在两个图形之间;
④若五边形ABCDE与五边形A′B′C′D′E′位似;
则其中 △ABC 与 △A′B′C′ 也是位似的,且位似比相等.
其中正确的有 .
①④
从来没有人读书,只有人在书中读自己,发现自己或检查自己.
——罗曼·罗兰
