2.2 第2课时 二次函数y=ax2和y=ax2+c的图象与性质 课件(共40张PPT) 2024-2025学年北师大版九年级数学下册
文档属性
| 名称 | 2.2 第2课时 二次函数y=ax2和y=ax2+c的图象与性质 课件(共40张PPT) 2024-2025学年北师大版九年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-04 13:38:24 | ||
图片预览


文档简介
(共40张PPT)
北师版·九年级下册
第2课时 二次函数y=ax 和y=ax +c的图象与性质
复习导入
y =-x2
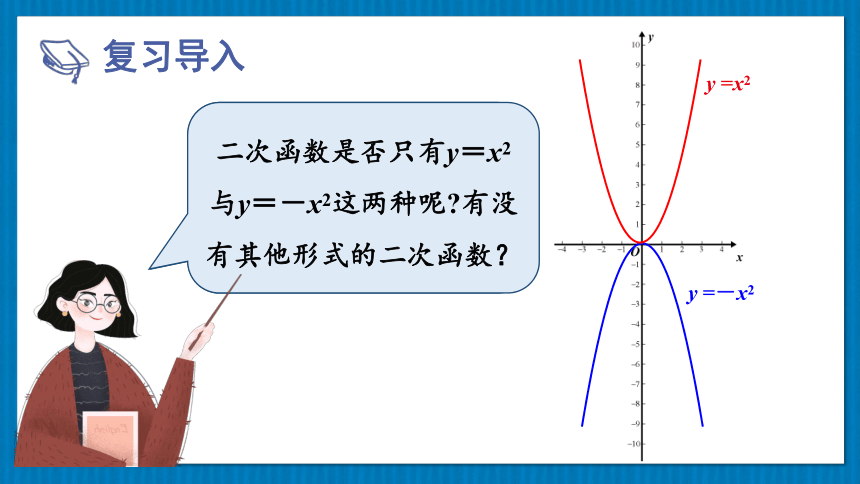
y =x2
二次函数y=x2与y=-x2的图象一样吗?它们有什么相同点?不同点?
二次函数是否只有y=x2与y=-x2这两种呢 有没有其他形式的二次函数?
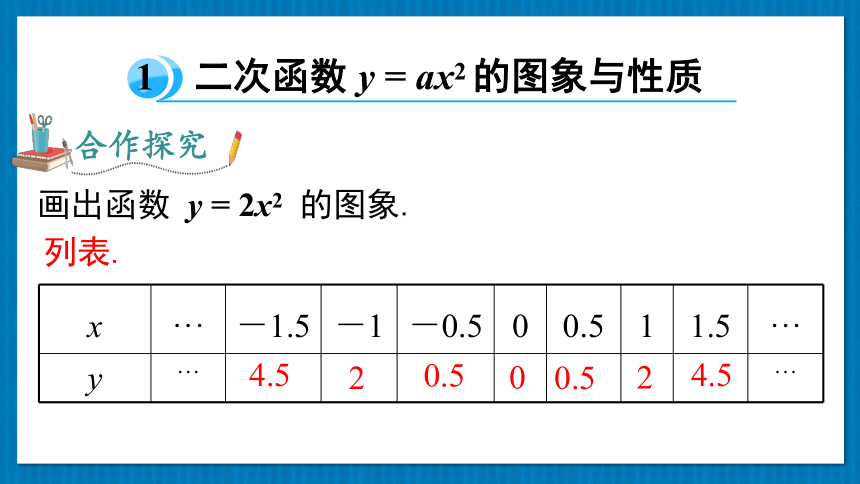
画出函数 y = 2x2 的图象.
列表.
x ··· -1.5 -1 -0.5 0 0.5 1 1.5 ···
y ··· ···
4.5
2
0.5
0
4.5
2
0.5
二次函数 y = ax2 的图象与性质
1
合作探究
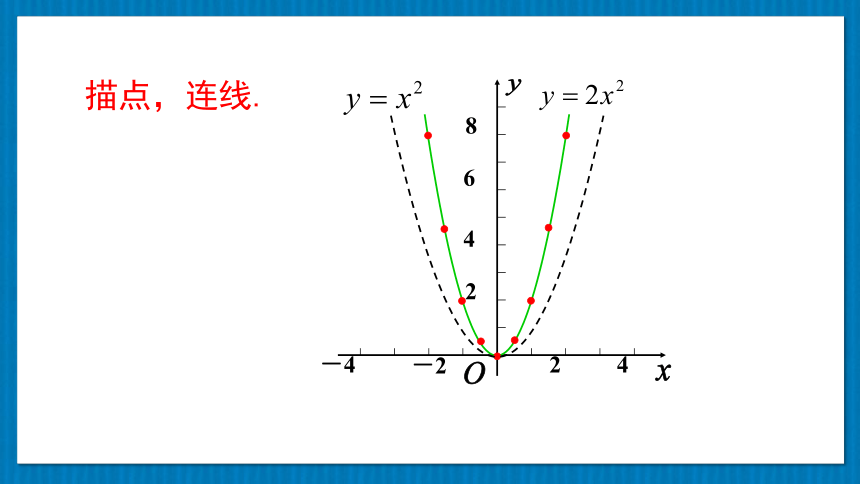
描点,连线.
x
y
O
-2
2
2
4
6
4
-4
8
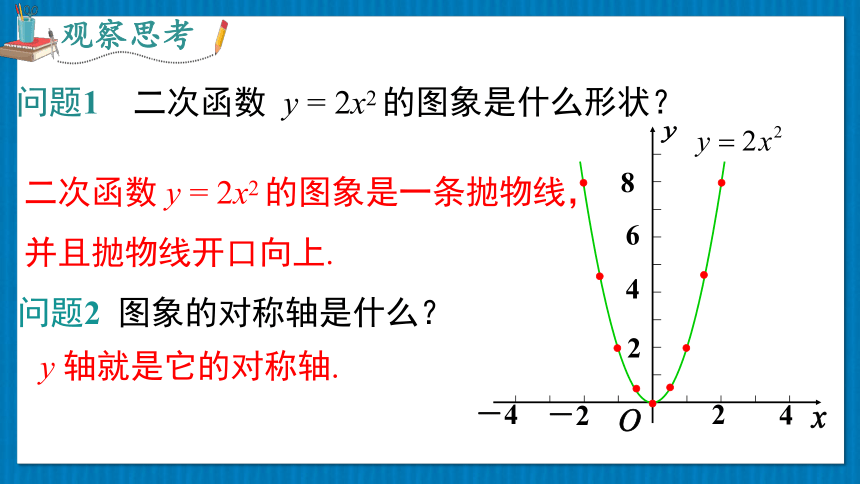
问题1 二次函数 y = 2x2 的图象是什么形状?
二次函数 y = 2x2 的图象是一条抛物线,
并且抛物线开口向上.
问题2 图象的对称轴是什么?
y 轴就是它的对称轴.
x
y
O
-2
2
2
4
6
4
-4
8
观察思考
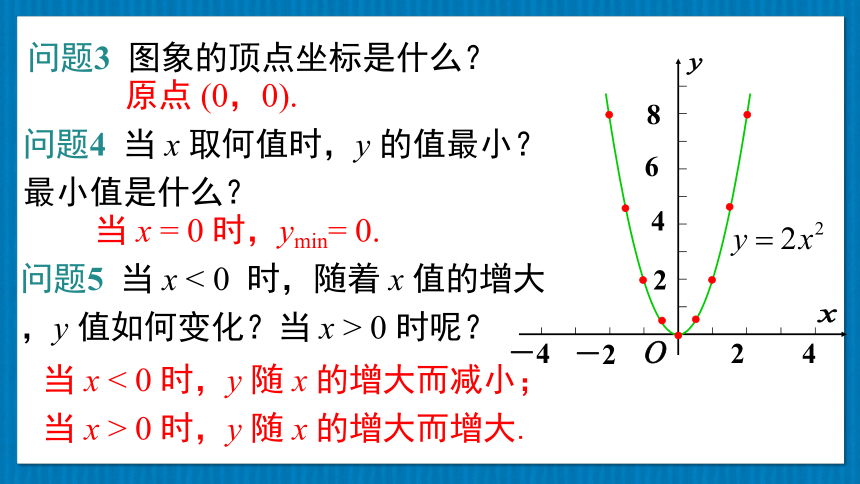
问题3 图象的顶点坐标是什么?
原点 (0,0).
问题4 当 x 取何值时,y 的值最小?
最小值是什么?
当 x = 0 时,ymin= 0.
x
y
O
-2
2
2
4
6
4
-4
8
当 x < 0 时,y 随 x 的增大而减小;当 x > 0 时,y 随 x 的增大而增大.
问题5 当 x < 0 时,随着 x 值的增大,y 值如何变化?当 x > 0 时呢?
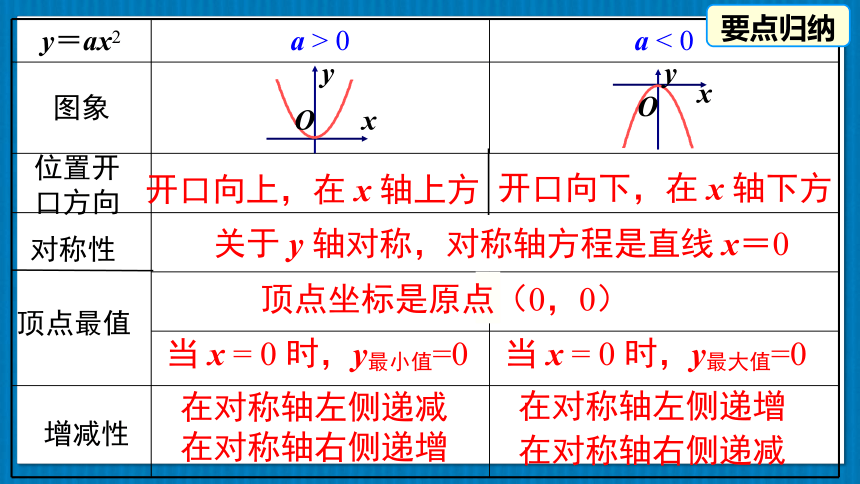
y=ax2 a > 0 a < 0
图象
位置开
口方向
对称性
顶点最值
增减性
开口向上,在 x 轴上方
开口向下,在 x 轴下方
关于 y 轴对称,对称轴方程是直线 x=0
当 x = 0 时,y最小值=0
当 x = 0 时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
要点归纳
y
O
x
y
O
x
顶点坐标是原点(0,0)
3. 函数 y = x2 的图象的开口 ,对称轴是 ,顶点是 ;顶点是抛物线的最____点.
2. 函数 y = -3x2 的图象的开口 ,对称轴是 ,顶点是_____ 顶点是 抛物线的最____点.
1. 函数 y = 4x2 的图象的开口 ,对称轴是 ,顶点是 ;
向上
向下
y轴
y 轴
(0,0)
(0,0)
4. 函数 y = -0.2x2 的图象的开口 ,对称轴是
,顶点是 .
向上
y轴
(0,0)
向下
y轴
(0,0)
高
低
练一练
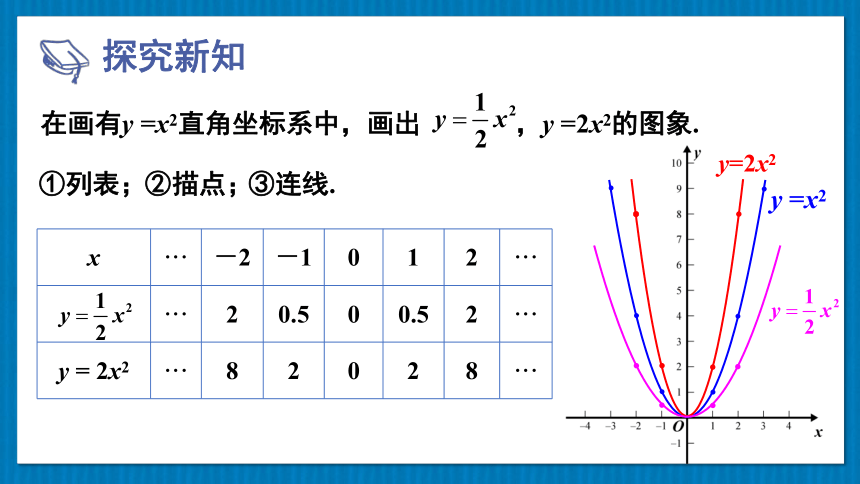
x ··· -2 -1 0 1 2 ···
··· 2 0.5 0 0.5 2 ···
y = 2x2 ··· 8 2 0 2 8 ···
在画有y =x2直角坐标系中,画出 ,y =2x2的图象.
探究新知
y =x2
①列表;
②描点;
③连线.
y=2x2
y =x2
y=2x2
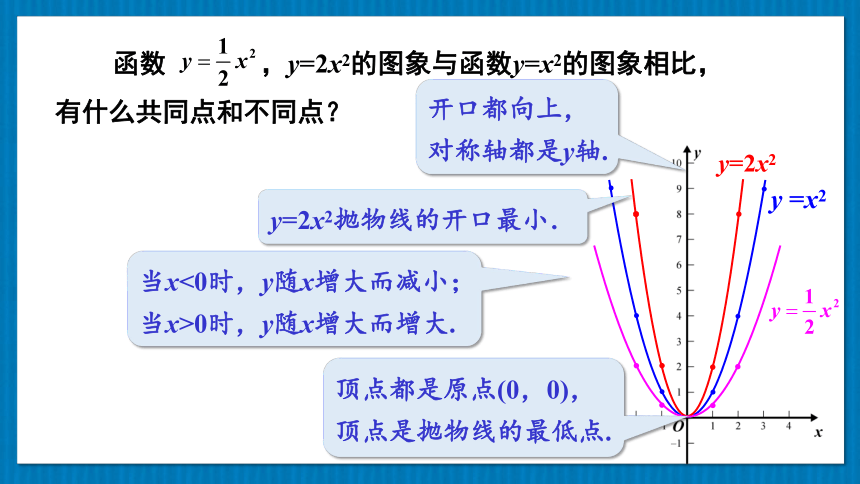
函数 ,y=2x2的图象与函数y=x2的图象相比,有什么共同点和不同点?
开口都向上,
对称轴都是y轴.
顶点都是原点(0,0),顶点是抛物线的最低点.
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
y=2x2抛物线的开口最小.
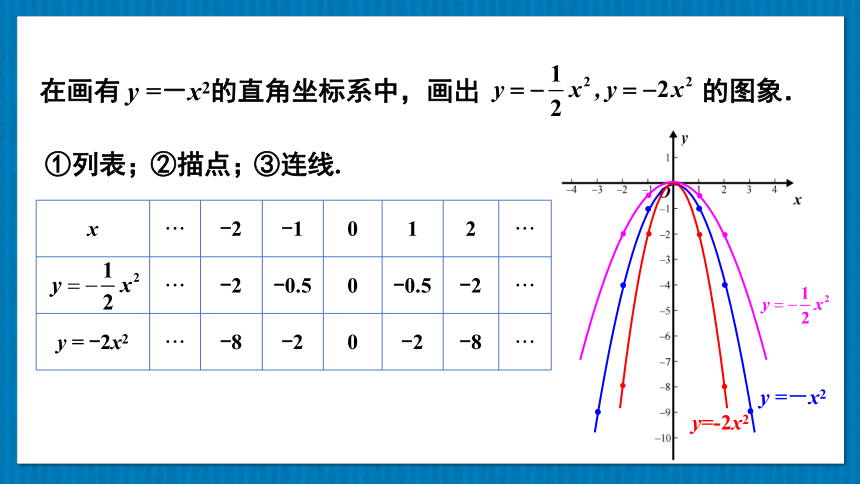
在画有 y =-x2的直角坐标系中,画出 的图象.
y =-x2
x ··· -2 -1 0 1 2 ···
··· -2 -0.5 0 -0.5 -2 ···
y = -2x2 ··· -8 -2 0 -2 -8 ···
①列表;
②描点;
③连线.
y=-2x2
y =-x2
y=-2x2
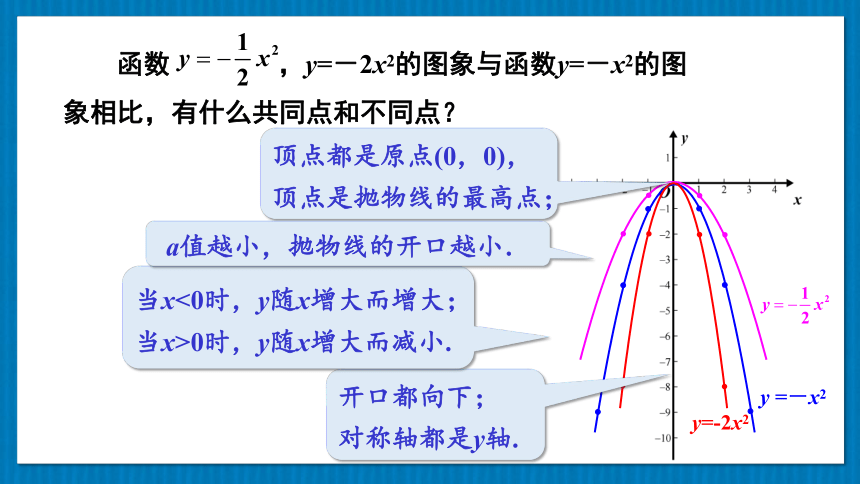
函数 ,y=-2x2的图象与函数y=-x2的图象相比,有什么共同点和不同点?
开口都向下;
对称轴都是y轴.
顶点都是原点(0,0),顶点是抛物线的最高点;
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
a值越小,抛物线的开口越小.
y=ax2 (a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增 减 性
最值
向上
向下
(0,0)
(0,0)
y轴 (x=0)
y轴 (x=0)
在对称轴的左侧,
y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,
y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
x=0时,y最小=0
x=0时,y最大=0
抛物线y=ax2 (a≠0)的形状是由|a|来确定的,一般说来,|a|越大,抛物线的开口就越小.
5.把图中图象的号码,填在它的函数式后面:(填序号)
(1)y = 3x2 的图象是_______;
(2)y = x2 的图象是_______;
(3)y = -x2 的图象是_______;
(4)y = x2 的图象是_______.
③
①
④
②
o
练一练
在画有y =2x2直角坐标系中,画出二次函数 y = 2x2 +1, y = 2x2 -1的图象。
x … -2 -1 0 1 2 …
y =2x2+1 … 9 3 1 3 9 …
y = 2x2 -1 … 7 1 -1 1 7 …
y=2x2
①列表;
y=2x2+1
y=2x2-1
②描点;
③连线.
y=2x2
y=2x2+1
y=2x2-1
二次函数y=2x2,y=2x2+1,y=2x2-1的图象都是抛物线,并且形状相同,只是位置不同.
将二次函数y=2x2的图象向上平移1个单位,就得到函数y=2x2+1的图象.
将二次函数y=2x2的图象向下平移1个单位,就得到函数y=2x2-1的图象.
将二次函数y=2x2+1的图象向____平移____个单位,就得到函数y=2x2-1的图象.
下
2
抛物线
y = 2x2+1 , y = 2x2 -1
y=2x2
与抛物线
有什么关系?
二次函数 y = ax2+c 的图象可以由 y = ax2 的图象平移得到:
当c > 0 时,向上平移 c 个单位长度得到.
当c < 0 时,向下平移 -c 个单位长度得到.
二次函数 y = ax2 与 y = ax2+c(a ≠ 0)的图象的关系
上下平移规律:
平方项不变,常数项上加下减.
要点归纳
抛物线y=ax2+c的图象相当于把抛物线y=ax2的图象____(c>0)或 (c<0)平移 个单位.
抛物线
y = 2x2+1 , y = 2x2 -1
y=2x2
与抛物线
有什么关系?
y=ax2+c
y=ax2
y = ax2
c
y = ax2+c(c>0)
c
y = ax2+c(c<0)
向上
向下
|c|
6. (湖州中考)将抛物线 y=x2 向上平移 3 个单位,所得抛物线的解析式( )
A.y=x2+3 B.y=x2-3
C.y=(x+3)2 D.y=(x-3)2
A
练一练
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
问题 抛物线 y = 2x2+1, y = 2x2-1的开口方向、对称轴和顶点各是什么?
y =2x2
y =2x2+1
y = 2x2-1
二次函数
开口方向
顶点
坐标
对称
轴
向上
向上
(0,1)
(0,-1)
y 轴
y 轴
向上
(0,0)
y 轴
合作探究
问题 抛物线 y = 2x2+1, y = 2x2-1 的增减性又如何?
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
当 x < 0 时,y 随 x 的增大而减小;当 x > 0 时,y 随 x 的增大而增大.
根据图象回答下列问题:
(1) 图象的形状都是 ;
(2) 图形的开口方向 ;
(3) 对称轴都是 ;
(4) 从上而下顶点坐标分别是
_________________;
抛物线
向下
y 轴
(0,1),
(0, 1)
想一想
1
O
-1
1
x
y
-1
-2
y = -2x2 + 1
y = -2x2 - 1
(5)顶点都是最____点,函数都有最____值,从上而下最大值分别为_______、________.
(6) 函数的增减性都相同: __________________________
___________________________.
高
大
y = 1
y = 1
对称轴左侧 y 随 x 增大而增大,
对称轴右侧 y 随 x 增大而减小
1
O
-1
1
x
y
-1
-2
y = -2x2 + 1
y = -2x2 - 1
想一想:通过上述例子,函数 y = ax2 + c 的性质是什么?
二次函数y = ax2 +c的图象和性质:
a的符号 a>0 a<0
图象 c>0
c<0
开口方向
对称轴
顶点坐标
函数的增减性
最值
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,c)
(0,c)
x=0时,y最小值=c
x=0时,y最大值=c
随堂练习
1. 抛物线y=2x2+3可以由抛物线y=2x2向 平移 个单位得到.
2. 抛物线y=- x2+1向 平移 个单位后,会得到抛物线y=- x2.
3. 抛物线y=-2x2-5的开口方向 ,对称轴是 ,顶点坐标是 .
上
3
下
1
向下
y轴
(0,-5)
4. 下列各组抛物线中能够互相平移彼此得到对方的是( )
A. y=2x2与y=3x2 B. y= x2+2与y=2x2+
C. y=2x2与y=x2+2 D. y=x2与y=x2-2
D
5. 对于二次函数y=- x2+2,当x为xl和x2时,对应的函数值分别为y1和y2,若x1>x2>0,则y1与y2的大小关系是( )
A.y1>y2 B.y1B
开口向下
当x>0时,y随x增大而减小.
6. 写出下列各组函数图象的开口方向、对称轴和顶点.
(1)y= x2+3; (2)y=-3x2-4.
解:(1)开口向上,对称轴为y轴,顶点为(0,3).
(2)开口向下,对称轴为y轴,顶点为(0,-4).
7. 求抛物线y=2x2-1关于x轴对称的抛物线的解析式.
y=2x2-1
解:抛物线y=2x2-1关于x轴对称的抛物线的解析式为y=-2x2+1.
8. 二次函数y=3x2- 的图象与二次函数y=3x2的图象有什么关系?它是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?画图看一看.
解:二次函数 与y=3x2的图象都是抛物线,形状相同,只是位置不同.将二次函数y=3x2的图象向下平移 个单位长度,就得到 的图象.二次函数 与y=3x2的图象都是轴对称图形,它们的对称轴都是y轴(直线x=0),开口都向上,顶点坐标分别是 .
9. 二次函数 的图象与二次函数 的图象有什么关系?
解:二次函数 与二次函数 的图象都是抛物线,形状相同,只是位置不同.将二次函数 的图象向上平移1个单位长度,就得到二次函数 的图象.
想一想
1. 画抛物线 y = ax2+c 的图象有些方法?
2. 抛物线 y = ax2 + c 中的 a 决定什么?c 决定什么?它的对称轴是什么?顶点坐标怎样表示?
第一种方法:平移法,两步即第一步画 y = ax2的图象,再向上(或向下)平移︱c ︱单位.
第二种方法:描点法,三步即列表、描点和连线.
a 决定开口方向和大小;c 决定顶点的纵坐标.
对称轴为 y 轴;顶点坐标为(0,c).
例1 关于抛物线 y = x2 + 1 与 y = x2 1,下列说法正确的是( )
A.开口方向相同
B.顶点相同
C.对称轴相同
D.当 x>0 时,
y 随 x 的增大而增大
C
分析: y = x2 + 1 y = x2 1
开口方向:
顶点:
对称轴:
增减性:
向下
向上
(0,1)
(0, 1)
y 轴
y 轴
当 x>0 时,y 随 x 的增大而减小
当 x>0 时,y 随 x 的增大而增大
二次函数 y = ax2+c (a≠0) 的图象和性质
图象
性质
与 y = ax2的关系
1. 开口方向由 a 的符号决定;
2. c 决定顶点位置;
3.对称轴是 y 轴.
增减性结合开口方向和对称轴才能确定.
平移规律:
c 正向上;
c 负向下.
1. 填表:
函数 开口方向 顶点 对称轴 有最高(低)点
y = 3x2
y = 3x2+1
y = -4x2-5
向上
向上
向下
(0,0)
(0,1)
(0,-5)
y 轴
y 轴
y 轴
有最低点
有最低点
有最高点
2. 不画函数 y = -x2 和 y= -x2+1 的图象回答下面的问题:
(1) 抛物线 y = -x2 + 1 经过怎样的平移才能得到抛物线 y = -x2.
(2) 函数 y = -x2 + 1,当 x 时, y 随 x 的增大而减小;当 x 时,函数 y 有最大值,最大值 y是 ,其图象与 y 轴的交点坐标是 ,与 x 轴的交点坐标是 .
(3) 试说出抛物线 y = x2-3的开口方向、对称轴和顶点坐标.
向下平移 1 个单位.
>0
= 0
1
(0,1)
(-1,0),(1,0)
开口方向向上,对称轴是 y 轴,顶点坐标(0,-3).
3. 在平面直角坐标系 xOy 中,函数 y = 2x2 的图象经过点 M(x1,y1),N(x2,y2)两点,若 -4<x1<-2,0<x2<2,则 y1 与 y2 的大小关系是__________.
y1>y2
4. 在同一直角坐标系中,一次函数 y=ax+c和二次函数 y=ax2+c 的图象大致为( )
方法总结:熟记一次函数 y=kx+b 在不同情况下所在的象限,以及熟练掌握二次函数的有关性质(开口方向、对称轴、顶点坐标等)是解决问题的关键.
D
课堂小结
课后作业
习题2.3
1、2、3
北师版·九年级下册
第2课时 二次函数y=ax 和y=ax +c的图象与性质
复习导入
y =-x2
y =x2
二次函数y=x2与y=-x2的图象一样吗?它们有什么相同点?不同点?
二次函数是否只有y=x2与y=-x2这两种呢 有没有其他形式的二次函数?
画出函数 y = 2x2 的图象.
列表.
x ··· -1.5 -1 -0.5 0 0.5 1 1.5 ···
y ··· ···
4.5
2
0.5
0
4.5
2
0.5
二次函数 y = ax2 的图象与性质
1
合作探究
描点,连线.
x
y
O
-2
2
2
4
6
4
-4
8
问题1 二次函数 y = 2x2 的图象是什么形状?
二次函数 y = 2x2 的图象是一条抛物线,
并且抛物线开口向上.
问题2 图象的对称轴是什么?
y 轴就是它的对称轴.
x
y
O
-2
2
2
4
6
4
-4
8
观察思考
问题3 图象的顶点坐标是什么?
原点 (0,0).
问题4 当 x 取何值时,y 的值最小?
最小值是什么?
当 x = 0 时,ymin= 0.
x
y
O
-2
2
2
4
6
4
-4
8
当 x < 0 时,y 随 x 的增大而减小;当 x > 0 时,y 随 x 的增大而增大.
问题5 当 x < 0 时,随着 x 值的增大,y 值如何变化?当 x > 0 时呢?
y=ax2 a > 0 a < 0
图象
位置开
口方向
对称性
顶点最值
增减性
开口向上,在 x 轴上方
开口向下,在 x 轴下方
关于 y 轴对称,对称轴方程是直线 x=0
当 x = 0 时,y最小值=0
当 x = 0 时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
要点归纳
y
O
x
y
O
x
顶点坐标是原点(0,0)
3. 函数 y = x2 的图象的开口 ,对称轴是 ,顶点是 ;顶点是抛物线的最____点.
2. 函数 y = -3x2 的图象的开口 ,对称轴是 ,顶点是_____ 顶点是 抛物线的最____点.
1. 函数 y = 4x2 的图象的开口 ,对称轴是 ,顶点是 ;
向上
向下
y轴
y 轴
(0,0)
(0,0)
4. 函数 y = -0.2x2 的图象的开口 ,对称轴是
,顶点是 .
向上
y轴
(0,0)
向下
y轴
(0,0)
高
低
练一练
x ··· -2 -1 0 1 2 ···
··· 2 0.5 0 0.5 2 ···
y = 2x2 ··· 8 2 0 2 8 ···
在画有y =x2直角坐标系中,画出 ,y =2x2的图象.
探究新知
y =x2
①列表;
②描点;
③连线.
y=2x2
y =x2
y=2x2
函数 ,y=2x2的图象与函数y=x2的图象相比,有什么共同点和不同点?
开口都向上,
对称轴都是y轴.
顶点都是原点(0,0),顶点是抛物线的最低点.
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
y=2x2抛物线的开口最小.
在画有 y =-x2的直角坐标系中,画出 的图象.
y =-x2
x ··· -2 -1 0 1 2 ···
··· -2 -0.5 0 -0.5 -2 ···
y = -2x2 ··· -8 -2 0 -2 -8 ···
①列表;
②描点;
③连线.
y=-2x2
y =-x2
y=-2x2
函数 ,y=-2x2的图象与函数y=-x2的图象相比,有什么共同点和不同点?
开口都向下;
对称轴都是y轴.
顶点都是原点(0,0),顶点是抛物线的最高点;
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
a值越小,抛物线的开口越小.
y=ax2 (a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增 减 性
最值
向上
向下
(0,0)
(0,0)
y轴 (x=0)
y轴 (x=0)
在对称轴的左侧,
y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,
y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
x=0时,y最小=0
x=0时,y最大=0
抛物线y=ax2 (a≠0)的形状是由|a|来确定的,一般说来,|a|越大,抛物线的开口就越小.
5.把图中图象的号码,填在它的函数式后面:(填序号)
(1)y = 3x2 的图象是_______;
(2)y = x2 的图象是_______;
(3)y = -x2 的图象是_______;
(4)y = x2 的图象是_______.
③
①
④
②
o
练一练
在画有y =2x2直角坐标系中,画出二次函数 y = 2x2 +1, y = 2x2 -1的图象。
x … -2 -1 0 1 2 …
y =2x2+1 … 9 3 1 3 9 …
y = 2x2 -1 … 7 1 -1 1 7 …
y=2x2
①列表;
y=2x2+1
y=2x2-1
②描点;
③连线.
y=2x2
y=2x2+1
y=2x2-1
二次函数y=2x2,y=2x2+1,y=2x2-1的图象都是抛物线,并且形状相同,只是位置不同.
将二次函数y=2x2的图象向上平移1个单位,就得到函数y=2x2+1的图象.
将二次函数y=2x2的图象向下平移1个单位,就得到函数y=2x2-1的图象.
将二次函数y=2x2+1的图象向____平移____个单位,就得到函数y=2x2-1的图象.
下
2
抛物线
y = 2x2+1 , y = 2x2 -1
y=2x2
与抛物线
有什么关系?
二次函数 y = ax2+c 的图象可以由 y = ax2 的图象平移得到:
当c > 0 时,向上平移 c 个单位长度得到.
当c < 0 时,向下平移 -c 个单位长度得到.
二次函数 y = ax2 与 y = ax2+c(a ≠ 0)的图象的关系
上下平移规律:
平方项不变,常数项上加下减.
要点归纳
抛物线y=ax2+c的图象相当于把抛物线y=ax2的图象____(c>0)或 (c<0)平移 个单位.
抛物线
y = 2x2+1 , y = 2x2 -1
y=2x2
与抛物线
有什么关系?
y=ax2+c
y=ax2
y = ax2
c
y = ax2+c(c>0)
c
y = ax2+c(c<0)
向上
向下
|c|
6. (湖州中考)将抛物线 y=x2 向上平移 3 个单位,所得抛物线的解析式( )
A.y=x2+3 B.y=x2-3
C.y=(x+3)2 D.y=(x-3)2
A
练一练
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
问题 抛物线 y = 2x2+1, y = 2x2-1的开口方向、对称轴和顶点各是什么?
y =2x2
y =2x2+1
y = 2x2-1
二次函数
开口方向
顶点
坐标
对称
轴
向上
向上
(0,1)
(0,-1)
y 轴
y 轴
向上
(0,0)
y 轴
合作探究
问题 抛物线 y = 2x2+1, y = 2x2-1 的增减性又如何?
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
当 x < 0 时,y 随 x 的增大而减小;当 x > 0 时,y 随 x 的增大而增大.
根据图象回答下列问题:
(1) 图象的形状都是 ;
(2) 图形的开口方向 ;
(3) 对称轴都是 ;
(4) 从上而下顶点坐标分别是
_________________;
抛物线
向下
y 轴
(0,1),
(0, 1)
想一想
1
O
-1
1
x
y
-1
-2
y = -2x2 + 1
y = -2x2 - 1
(5)顶点都是最____点,函数都有最____值,从上而下最大值分别为_______、________.
(6) 函数的增减性都相同: __________________________
___________________________.
高
大
y = 1
y = 1
对称轴左侧 y 随 x 增大而增大,
对称轴右侧 y 随 x 增大而减小
1
O
-1
1
x
y
-1
-2
y = -2x2 + 1
y = -2x2 - 1
想一想:通过上述例子,函数 y = ax2 + c 的性质是什么?
二次函数y = ax2 +c的图象和性质:
a的符号 a>0 a<0
图象 c>0
c<0
开口方向
对称轴
顶点坐标
函数的增减性
最值
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,c)
(0,c)
x=0时,y最小值=c
x=0时,y最大值=c
随堂练习
1. 抛物线y=2x2+3可以由抛物线y=2x2向 平移 个单位得到.
2. 抛物线y=- x2+1向 平移 个单位后,会得到抛物线y=- x2.
3. 抛物线y=-2x2-5的开口方向 ,对称轴是 ,顶点坐标是 .
上
3
下
1
向下
y轴
(0,-5)
4. 下列各组抛物线中能够互相平移彼此得到对方的是( )
A. y=2x2与y=3x2 B. y= x2+2与y=2x2+
C. y=2x2与y=x2+2 D. y=x2与y=x2-2
D
5. 对于二次函数y=- x2+2,当x为xl和x2时,对应的函数值分别为y1和y2,若x1>x2>0,则y1与y2的大小关系是( )
A.y1>y2 B.y1
开口向下
当x>0时,y随x增大而减小.
6. 写出下列各组函数图象的开口方向、对称轴和顶点.
(1)y= x2+3; (2)y=-3x2-4.
解:(1)开口向上,对称轴为y轴,顶点为(0,3).
(2)开口向下,对称轴为y轴,顶点为(0,-4).
7. 求抛物线y=2x2-1关于x轴对称的抛物线的解析式.
y=2x2-1
解:抛物线y=2x2-1关于x轴对称的抛物线的解析式为y=-2x2+1.
8. 二次函数y=3x2- 的图象与二次函数y=3x2的图象有什么关系?它是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?画图看一看.
解:二次函数 与y=3x2的图象都是抛物线,形状相同,只是位置不同.将二次函数y=3x2的图象向下平移 个单位长度,就得到 的图象.二次函数 与y=3x2的图象都是轴对称图形,它们的对称轴都是y轴(直线x=0),开口都向上,顶点坐标分别是 .
9. 二次函数 的图象与二次函数 的图象有什么关系?
解:二次函数 与二次函数 的图象都是抛物线,形状相同,只是位置不同.将二次函数 的图象向上平移1个单位长度,就得到二次函数 的图象.
想一想
1. 画抛物线 y = ax2+c 的图象有些方法?
2. 抛物线 y = ax2 + c 中的 a 决定什么?c 决定什么?它的对称轴是什么?顶点坐标怎样表示?
第一种方法:平移法,两步即第一步画 y = ax2的图象,再向上(或向下)平移︱c ︱单位.
第二种方法:描点法,三步即列表、描点和连线.
a 决定开口方向和大小;c 决定顶点的纵坐标.
对称轴为 y 轴;顶点坐标为(0,c).
例1 关于抛物线 y = x2 + 1 与 y = x2 1,下列说法正确的是( )
A.开口方向相同
B.顶点相同
C.对称轴相同
D.当 x>0 时,
y 随 x 的增大而增大
C
分析: y = x2 + 1 y = x2 1
开口方向:
顶点:
对称轴:
增减性:
向下
向上
(0,1)
(0, 1)
y 轴
y 轴
当 x>0 时,y 随 x 的增大而减小
当 x>0 时,y 随 x 的增大而增大
二次函数 y = ax2+c (a≠0) 的图象和性质
图象
性质
与 y = ax2的关系
1. 开口方向由 a 的符号决定;
2. c 决定顶点位置;
3.对称轴是 y 轴.
增减性结合开口方向和对称轴才能确定.
平移规律:
c 正向上;
c 负向下.
1. 填表:
函数 开口方向 顶点 对称轴 有最高(低)点
y = 3x2
y = 3x2+1
y = -4x2-5
向上
向上
向下
(0,0)
(0,1)
(0,-5)
y 轴
y 轴
y 轴
有最低点
有最低点
有最高点
2. 不画函数 y = -x2 和 y= -x2+1 的图象回答下面的问题:
(1) 抛物线 y = -x2 + 1 经过怎样的平移才能得到抛物线 y = -x2.
(2) 函数 y = -x2 + 1,当 x 时, y 随 x 的增大而减小;当 x 时,函数 y 有最大值,最大值 y是 ,其图象与 y 轴的交点坐标是 ,与 x 轴的交点坐标是 .
(3) 试说出抛物线 y = x2-3的开口方向、对称轴和顶点坐标.
向下平移 1 个单位.
>0
= 0
1
(0,1)
(-1,0),(1,0)
开口方向向上,对称轴是 y 轴,顶点坐标(0,-3).
3. 在平面直角坐标系 xOy 中,函数 y = 2x2 的图象经过点 M(x1,y1),N(x2,y2)两点,若 -4<x1<-2,0<x2<2,则 y1 与 y2 的大小关系是__________.
y1>y2
4. 在同一直角坐标系中,一次函数 y=ax+c和二次函数 y=ax2+c 的图象大致为( )
方法总结:熟记一次函数 y=kx+b 在不同情况下所在的象限,以及熟练掌握二次函数的有关性质(开口方向、对称轴、顶点坐标等)是解决问题的关键.
D
课堂小结
课后作业
习题2.3
1、2、3
