山东省泰安第六中学2016届九年级3月月考数学试题
文档属性
| 名称 | 山东省泰安第六中学2016届九年级3月月考数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 225.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-28 13:01:39 | ||
图片预览

文档简介
泰安六中九年级数学月考测试题(2016年3月)
一、选择题(共20小题,每题3分,共60分)
1. 据报道,2014年第一季度,广东省实现地区生产总值约1.36万亿元,用科学记数法表示为: ( )
A. 0.136×10 12元 B. 1.36×10 12元 C. 1.36×10 11元 D. 13.6×10 11元
2. 一个几何体的三视图如图所示,则这个几何体是 ( )
A. B. C. D.
3. 下列计算正确的是( )
A. B. C. D.
4. 张华想给老师发短信拜年,可一时记 ( http: / / www.21cnjy.com )不清老师手机号码后三位数的顺序,只记得是1,6,9三个数字,则张华一次发短信成功的概率是( )
A. B. C. D.
5. 节日期间,某专卖店推出全店打8折的 ( http: / / www.21cnjy.com )优惠活动,持贵宾卡可在8折基础上再打9折,小明妈妈持贵宾卡买了一件商品共花了 a元,则该商品的标价是( )
A. 元 B. 元 C. 元 D. 元
6. 已知a+b=2,则a 2-b 2+4b的值是( )
A. 2 B. 3 C. 4 D. 6
7. 已知A、B两地相 ( http: / / www.21cnjy.com )距 126 km,一辆小汽车和一辆货车分别从A、B两地同时出发,相向而行,经过45分钟相遇,相遇时小汽车比货车多行 6 km,设小汽车和货车的速度分别为 xkm/h, ykm/h,则下列方程组正确的是( )
A. B. C.
D. ( http: / / www.21cnjy.com )
8. 若关于x的一元二次方程(k 1)x 2+2x 2=0有不相等实数根,则k的取值范围是 ( )
A. k> B. k≥ C. k> 且k≠1 D. k≥ 且k≠1
9. 如果a、b是方程x 2-3x+1=0 的两根,那么代数式a 2+2b 2-3b的值为 ( )
A. 6 B. -6 C. 7 D. -7
10. 已知关于 的不等式组 有且只有1个整数解,则 的取值范围是( )
A. B. C. D.
11. 函数y=中自变量x的取值范围是( )
A. x≥2且x≠-3 B. x≥2 C. x≠-3 D. x>2且x≠-3
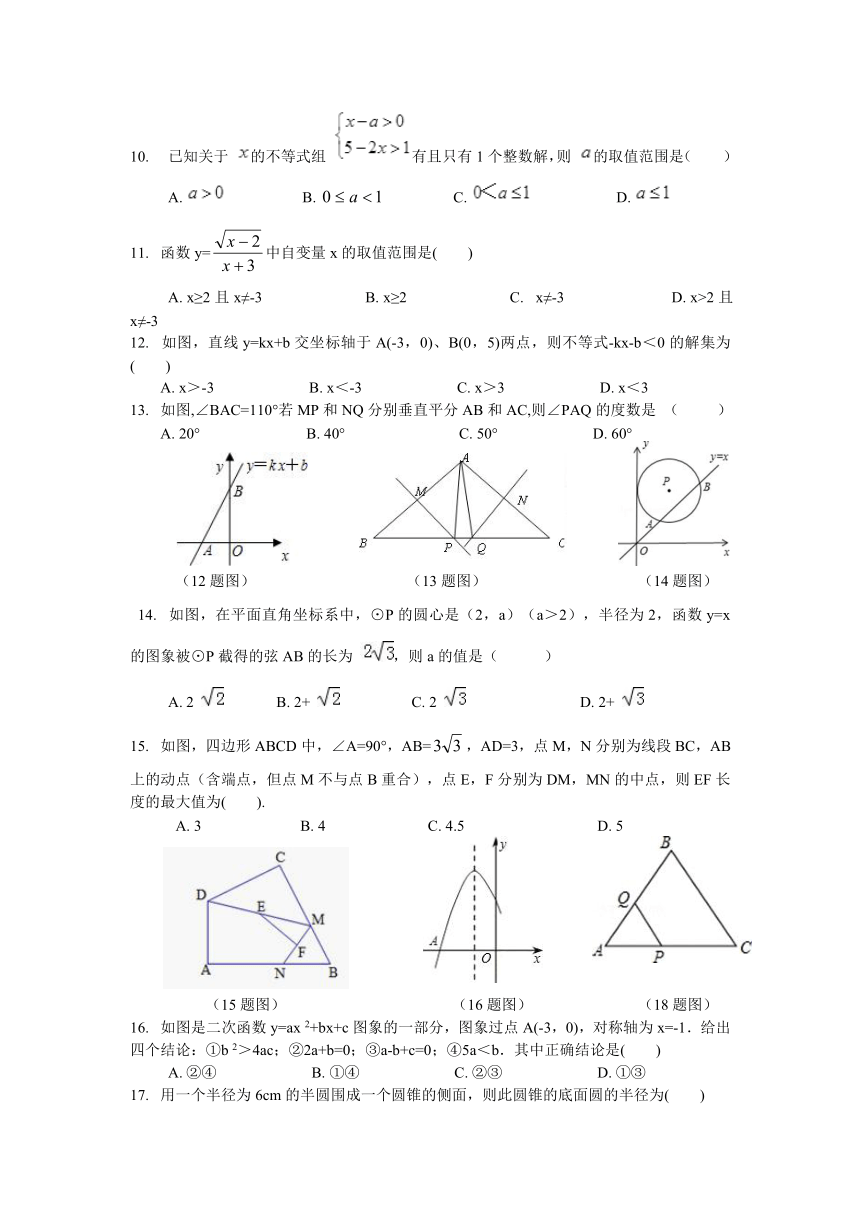
12. 如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,5)两点,则不等式-kx-b<0的解集为( )
A. x>-3 B. x<-3 C. x>3 D. x<3
13. 如图,∠BAC=110°若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是 ( )
A. 20° B. 40° C. 50° D. 60°
(12题图) (13题图) (14题图)
14. 如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ,则a的值是( )
A. 2 B. 2+ C. 2 D. 2+
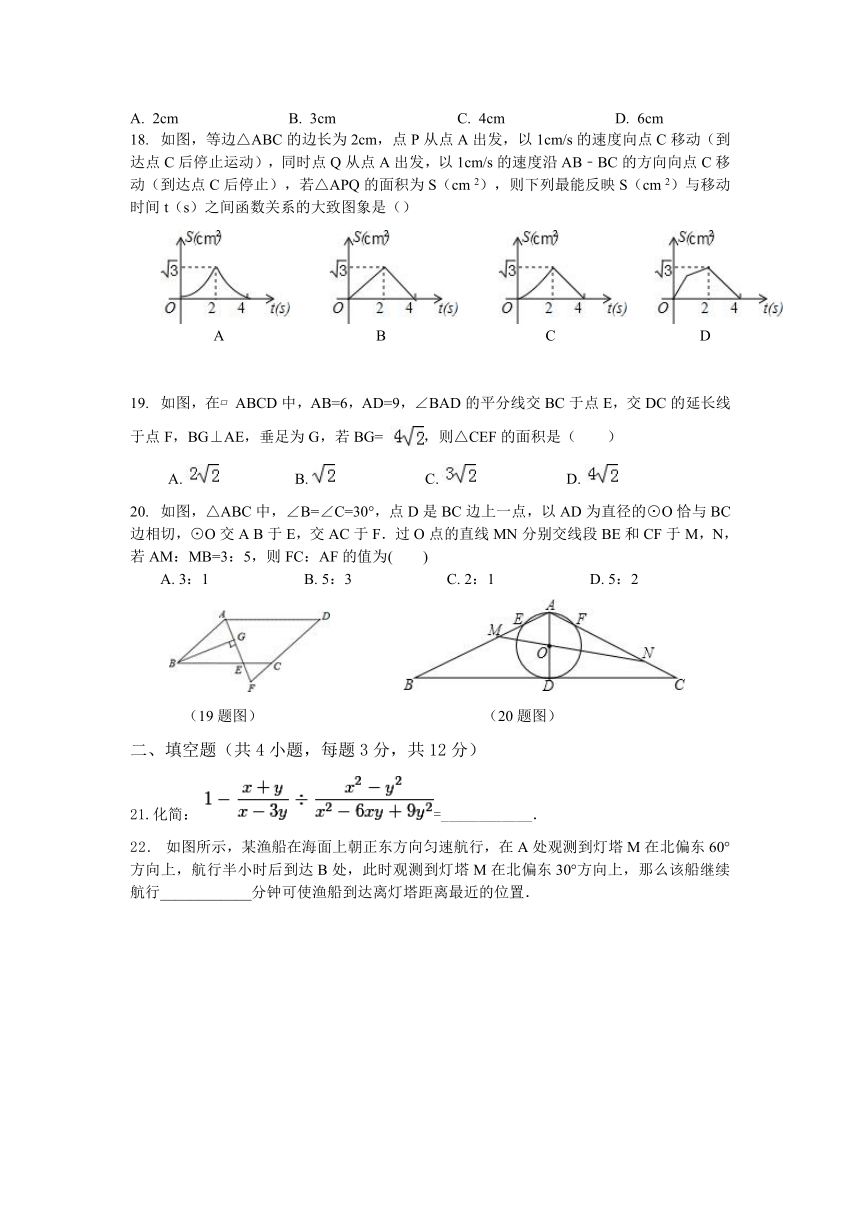
15. 如图,四边形ABCD中,∠A=90°,AB=,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( ).
A. 3 B. 4 C. 4.5 D. 5
(15题图) (16题图) (18题图)
16. 如图是二次函数y=ax 2+bx ( http: / / www.21cnjy.com )+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b 2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是( )
A. ②④ B. ①④ C. ②③ D. ①③
17. 用一个半径为6cm的半圆围成一个圆锥的侧面,则此圆锥的底面圆的半径为( )
A. 2cm B. 3cm C. 4cm D. 6cm
18. 如图,等边△ABC的边长为 ( http: / / www.21cnjy.com )2cm,点P从点A出发,以1cm/s的速度向点C移动(到达点C后停止运动),同时点Q从点A出发,以1cm/s的速度沿AB﹣BC的方向向点C移动(到达点C后停止),若△APQ的面积为S(cm 2),则下列最能反映S(cm 2)与移动时间t(s)之间函数关系的大致图象是()
A B C D
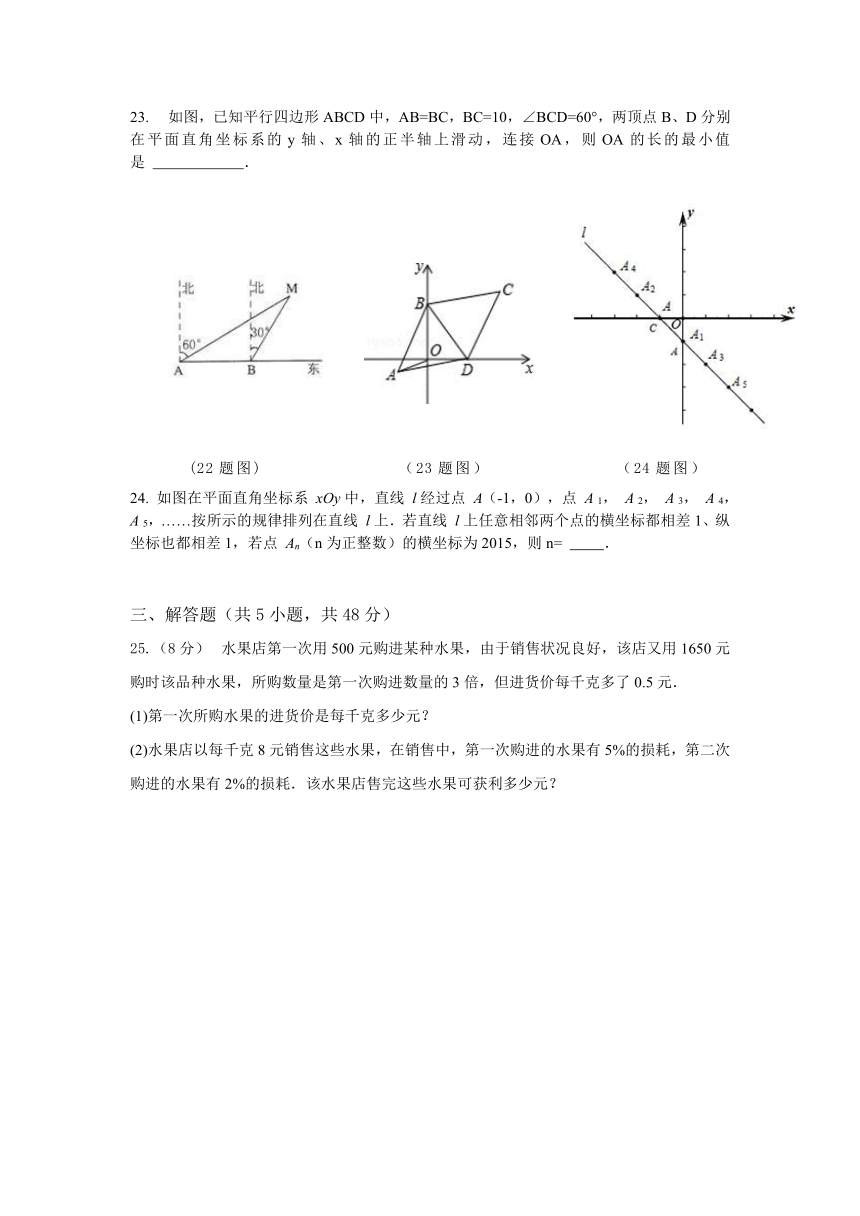
19. 如图,在 ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG= ,则△CEF的面积是( )
A. B. C. D.
20. 如图,△ABC中,∠B ( http: / / www.21cnjy.com )=∠C=30°,点D是BC边上一点,以AD为直径的⊙O恰与BC边相切,⊙O交A B于E,交AC于F.过O点的直线MN分别交线段BE和CF于M,N,若AM:MB=3:5,则FC:AF的值为( )
A. 3:1 B. 5:3 C. 2:1 D. 5:2
(19题图) (20题图)
二、填空题(共4小题,每题3分,共12分)
21.化简: =____________.
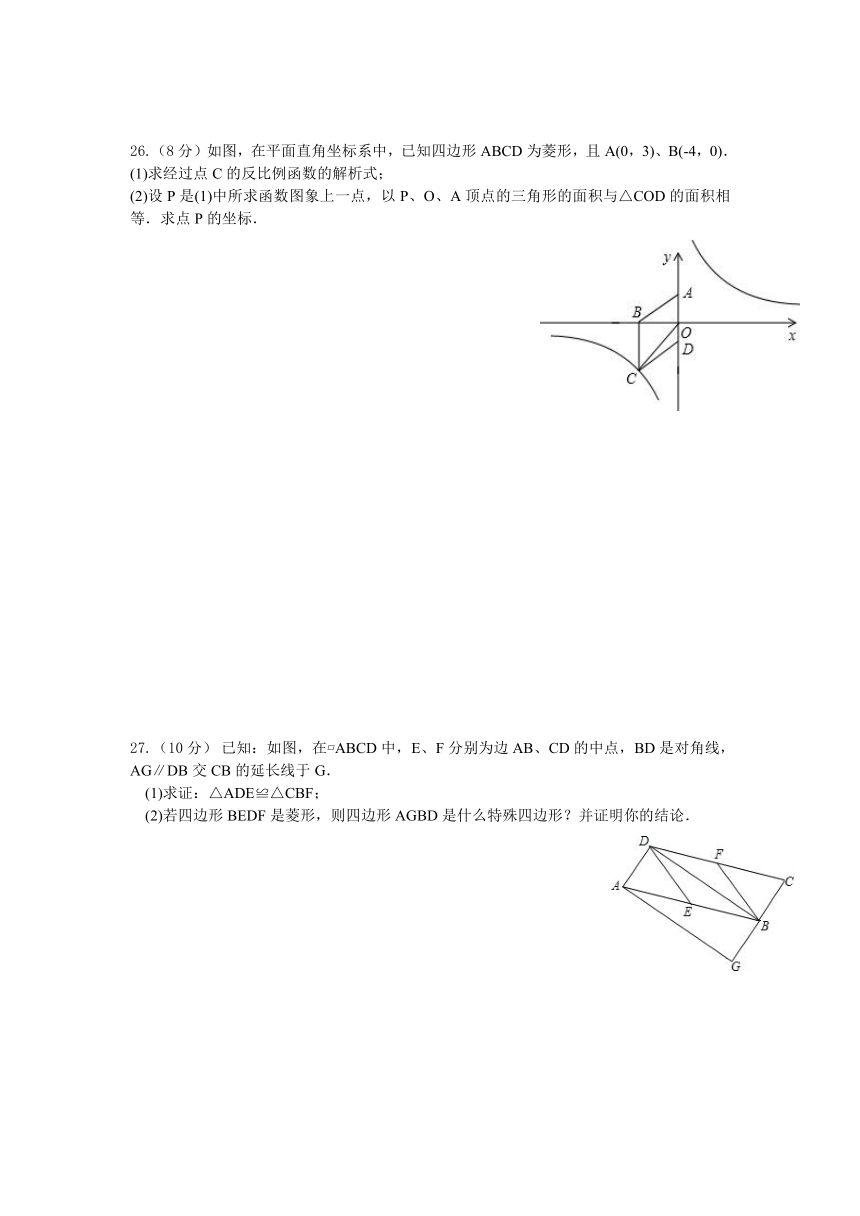
22. 如图所示,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行____________分钟可使渔船到达离灯塔距离最近的位置.
23. 如图,已知平行四边形 ( http: / / www.21cnjy.com )ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是 .
(22题图) (23题图) (24题图)
24. 如图在平面直角坐标系 xOy ( http: / / www.21cnjy.com )中,直线 l经过点 A(-1,0),点 A 1, A 2, A 3, A 4, A 5,……按所示的规律排列在直线 l上.若直线 l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,若点 An(n为正整数)的横坐标为2015,则n= .
三、解答题(共5小题,共48分)
25.(8分) 水果店第一次 ( http: / / www.21cnjy.com )用500元购进某种水果,由于销售状况良好,该店又用1650元购时该品种水果,所购数量是第一次购进数量的3倍,但进货价每千克多了0.5元.
(1)第一次所购水果的进货价是每千克多少元?
(2)水果店以每千克8元销售这些水果,在销售中,第一次购进的水果有5%的损耗,第二次购进的水果有2%的损耗.该水果店售完这些水果可获利多少元?
26.(8分)如图,在平面直角坐标系中 ( http: / / www.21cnjy.com ),已知四边形ABCD为菱形,且A(0,3)、B(-4,0).
(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COD的面积相等.求点P的坐标.
27.(10分) 已知:如图,在 ABCD ( http: / / www.21cnjy.com )中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
28.(10分)如下图1,在四边形ABCD中,点E、F分别是AB、CD的中点.过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连结GA、GB、GC、GD、EF,若∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求的值.
29.(12分) 如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)、B(3,0)两点,直线y=x-2与x轴交于点D,与y轴交于点C.点P是x轴下方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式:
(2)若PE=3EF,求m的值;
(3)连接PC,是否存在点P,使△PCE为等腰直角三角形?若存在,请直接写出相应的点P的横坐标m的值;若不存在,请说明理由.
(备用图)
2016年九年级数学月考试题答案
一.选择题:
1-----5. B C D A D 6-----10. C D C A B
11-----15. B A B B A 16------20. B B C A A
二.填空题:
21. 22. 15 23. 24. 4031
三.解答题:
25. 解:(1)设第一次所购水果的进货价是每千克x元,依题意,得 ,
解得,x=5,经检查,x=5是原方程的解.
答:第一次进货价为5元; (5分)
(2)第一次购进:500÷5=100千克,第二次购进:3×100=300千克,
获利:[100×(1-5%)×8-500]+[300×(1-2%)×8-1650]=962元.
答:第一次所购水果的进货价是每千克5元,该水果店售完这些水果可获利962元. (8分)
26. 解:(1)由题意知,OA=3,OB=4
在Rt△AOB中,AB=
∵四边形ABCD为菱形
∴AD=BC=AB=5,
∴C(-4,-5). 设经过点C的反比例函数的解析式为 (k≠0),
则 =-5,解得k=20. 故所求的反比例函数的解析式为 . (4分)
(2)设P(x,y)
∵AD=AB=5,OA=3,
∴OD=2,S △COD=
即 ,
∴|x|= , ∴
当x= 时,y= = ,当x=- 时,y= =-
∴P( )或( ). (8分)
27.
(1)证明:∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE= AB,CF= CD.
∴AE=CF.
在△AED与△CBF中,
∴△ADE≌△CBF(SAS). (4分)
(2)解:当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴四边形AGBD是矩形. (6分)
28. (1)证明:∵GE是AB的垂直平分线,∴GA=GB.
同理GD=GC.
在△AGD和△BGC中,∵GA=GB,∠AGD=∠BGC,GD=GC,
∴△AGD≌△BGC.∴AD=BC.(3分)
(2)证明:∵∠AGD=∠BGC,∴∠AGB=∠DGC.
在△AGB和△DGC中,=,∠AGB=∠DGC,
∴△AGB∽△DGC.
∴=.又∠AGE=∠DGF,∴∠AGD=∠EGF,∴△AGD∽△EGF.(7分)
(3)如图1,延长AD交GB于点M,交BC的延长线于点H,则AH⊥BH.
由△AGD≌△BGC,知∠GAD=∠GBC.
在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB.
∴∠AGB=∠AHB=90°,
∴∠AGE=∠AGB=45°,
∴=.
又△AGD∽△EGF,
∴==.(10分)
(本小题解法有多种,如可按图2和图3作辅助线求解,过程略)
29.
解:(1)把A(-1,0)、B(3,0),两点的坐标代入y=ax2+bx-3得:
解得:,
所以,这条抛物线的解析这式为:y=x2-2x-3;(3分)
(2)设点P的横坐标是m,则P(m,m2-2m-3),E(m,m-2)F(m,0),
PE=|yE-yP|=|(m-2)-(m2-2m-3)|=|-m2+3m+1|,
EF=|-m+2|,
由题意PE=3EF,即:|-m2+3m+1|=3|-m+2|,
①若-m2+3m+1=3(-m+2),
整理得:m2-6m+5=0,
解得:m=1或m=5,
∵P在x轴下方,
∴-1<m<3,
∴m=5不合题意应舍去,
∴m=1,
②若-m2+3m+1=-3(-m+2),
整理得:m2-7=0,
解得:m=或m=-,
∵P在x轴下方,
∴-1<m<3,m=-不合题意应舍去,
∴m=,
综上所述,m=1或m=;(8分)
(3)存在点P的横坐标为:m=1±,或或.
理由如下:直线y=x-2与y轴的夹角为45°,
①∠PCE=90°时,直线PC的解析式为y=-x-2,
联立,
消掉y得,x2-x-1=0,
解得或,
所以,点P的横坐标或;
②∠CPE=90°时,PC∥x轴,
∵点C(0,-2),
∴点P与点C的纵坐标相等,为-2,
∴x2-2x-3=-2,
解得x=1±,
综上所述,点P的横坐标m=1±,或或.(12分)
一、选择题(共20小题,每题3分,共60分)
1. 据报道,2014年第一季度,广东省实现地区生产总值约1.36万亿元,用科学记数法表示为: ( )
A. 0.136×10 12元 B. 1.36×10 12元 C. 1.36×10 11元 D. 13.6×10 11元
2. 一个几何体的三视图如图所示,则这个几何体是 ( )
A. B. C. D.
3. 下列计算正确的是( )
A. B. C. D.
4. 张华想给老师发短信拜年,可一时记 ( http: / / www.21cnjy.com )不清老师手机号码后三位数的顺序,只记得是1,6,9三个数字,则张华一次发短信成功的概率是( )
A. B. C. D.
5. 节日期间,某专卖店推出全店打8折的 ( http: / / www.21cnjy.com )优惠活动,持贵宾卡可在8折基础上再打9折,小明妈妈持贵宾卡买了一件商品共花了 a元,则该商品的标价是( )
A. 元 B. 元 C. 元 D. 元
6. 已知a+b=2,则a 2-b 2+4b的值是( )
A. 2 B. 3 C. 4 D. 6
7. 已知A、B两地相 ( http: / / www.21cnjy.com )距 126 km,一辆小汽车和一辆货车分别从A、B两地同时出发,相向而行,经过45分钟相遇,相遇时小汽车比货车多行 6 km,设小汽车和货车的速度分别为 xkm/h, ykm/h,则下列方程组正确的是( )
A. B. C.
D. ( http: / / www.21cnjy.com )
8. 若关于x的一元二次方程(k 1)x 2+2x 2=0有不相等实数根,则k的取值范围是 ( )
A. k> B. k≥ C. k> 且k≠1 D. k≥ 且k≠1
9. 如果a、b是方程x 2-3x+1=0 的两根,那么代数式a 2+2b 2-3b的值为 ( )
A. 6 B. -6 C. 7 D. -7
10. 已知关于 的不等式组 有且只有1个整数解,则 的取值范围是( )
A. B. C. D.
11. 函数y=中自变量x的取值范围是( )
A. x≥2且x≠-3 B. x≥2 C. x≠-3 D. x>2且x≠-3
12. 如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,5)两点,则不等式-kx-b<0的解集为( )
A. x>-3 B. x<-3 C. x>3 D. x<3
13. 如图,∠BAC=110°若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是 ( )
A. 20° B. 40° C. 50° D. 60°
(12题图) (13题图) (14题图)
14. 如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ,则a的值是( )
A. 2 B. 2+ C. 2 D. 2+
15. 如图,四边形ABCD中,∠A=90°,AB=,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( ).
A. 3 B. 4 C. 4.5 D. 5
(15题图) (16题图) (18题图)
16. 如图是二次函数y=ax 2+bx ( http: / / www.21cnjy.com )+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b 2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是( )
A. ②④ B. ①④ C. ②③ D. ①③
17. 用一个半径为6cm的半圆围成一个圆锥的侧面,则此圆锥的底面圆的半径为( )
A. 2cm B. 3cm C. 4cm D. 6cm
18. 如图,等边△ABC的边长为 ( http: / / www.21cnjy.com )2cm,点P从点A出发,以1cm/s的速度向点C移动(到达点C后停止运动),同时点Q从点A出发,以1cm/s的速度沿AB﹣BC的方向向点C移动(到达点C后停止),若△APQ的面积为S(cm 2),则下列最能反映S(cm 2)与移动时间t(s)之间函数关系的大致图象是()
A B C D
19. 如图,在 ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG= ,则△CEF的面积是( )
A. B. C. D.
20. 如图,△ABC中,∠B ( http: / / www.21cnjy.com )=∠C=30°,点D是BC边上一点,以AD为直径的⊙O恰与BC边相切,⊙O交A B于E,交AC于F.过O点的直线MN分别交线段BE和CF于M,N,若AM:MB=3:5,则FC:AF的值为( )
A. 3:1 B. 5:3 C. 2:1 D. 5:2
(19题图) (20题图)
二、填空题(共4小题,每题3分,共12分)
21.化简: =____________.
22. 如图所示,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行____________分钟可使渔船到达离灯塔距离最近的位置.
23. 如图,已知平行四边形 ( http: / / www.21cnjy.com )ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是 .
(22题图) (23题图) (24题图)
24. 如图在平面直角坐标系 xOy ( http: / / www.21cnjy.com )中,直线 l经过点 A(-1,0),点 A 1, A 2, A 3, A 4, A 5,……按所示的规律排列在直线 l上.若直线 l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,若点 An(n为正整数)的横坐标为2015,则n= .
三、解答题(共5小题,共48分)
25.(8分) 水果店第一次 ( http: / / www.21cnjy.com )用500元购进某种水果,由于销售状况良好,该店又用1650元购时该品种水果,所购数量是第一次购进数量的3倍,但进货价每千克多了0.5元.
(1)第一次所购水果的进货价是每千克多少元?
(2)水果店以每千克8元销售这些水果,在销售中,第一次购进的水果有5%的损耗,第二次购进的水果有2%的损耗.该水果店售完这些水果可获利多少元?
26.(8分)如图,在平面直角坐标系中 ( http: / / www.21cnjy.com ),已知四边形ABCD为菱形,且A(0,3)、B(-4,0).
(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COD的面积相等.求点P的坐标.
27.(10分) 已知:如图,在 ABCD ( http: / / www.21cnjy.com )中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
28.(10分)如下图1,在四边形ABCD中,点E、F分别是AB、CD的中点.过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连结GA、GB、GC、GD、EF,若∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求的值.
29.(12分) 如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)、B(3,0)两点,直线y=x-2与x轴交于点D,与y轴交于点C.点P是x轴下方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式:
(2)若PE=3EF,求m的值;
(3)连接PC,是否存在点P,使△PCE为等腰直角三角形?若存在,请直接写出相应的点P的横坐标m的值;若不存在,请说明理由.
(备用图)
2016年九年级数学月考试题答案
一.选择题:
1-----5. B C D A D 6-----10. C D C A B
11-----15. B A B B A 16------20. B B C A A
二.填空题:
21. 22. 15 23. 24. 4031
三.解答题:
25. 解:(1)设第一次所购水果的进货价是每千克x元,依题意,得 ,
解得,x=5,经检查,x=5是原方程的解.
答:第一次进货价为5元; (5分)
(2)第一次购进:500÷5=100千克,第二次购进:3×100=300千克,
获利:[100×(1-5%)×8-500]+[300×(1-2%)×8-1650]=962元.
答:第一次所购水果的进货价是每千克5元,该水果店售完这些水果可获利962元. (8分)
26. 解:(1)由题意知,OA=3,OB=4
在Rt△AOB中,AB=
∵四边形ABCD为菱形
∴AD=BC=AB=5,
∴C(-4,-5). 设经过点C的反比例函数的解析式为 (k≠0),
则 =-5,解得k=20. 故所求的反比例函数的解析式为 . (4分)
(2)设P(x,y)
∵AD=AB=5,OA=3,
∴OD=2,S △COD=
即 ,
∴|x|= , ∴
当x= 时,y= = ,当x=- 时,y= =-
∴P( )或( ). (8分)
27.
(1)证明:∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE= AB,CF= CD.
∴AE=CF.
在△AED与△CBF中,
∴△ADE≌△CBF(SAS). (4分)
(2)解:当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴四边形AGBD是矩形. (6分)
28. (1)证明:∵GE是AB的垂直平分线,∴GA=GB.
同理GD=GC.
在△AGD和△BGC中,∵GA=GB,∠AGD=∠BGC,GD=GC,
∴△AGD≌△BGC.∴AD=BC.(3分)
(2)证明:∵∠AGD=∠BGC,∴∠AGB=∠DGC.
在△AGB和△DGC中,=,∠AGB=∠DGC,
∴△AGB∽△DGC.
∴=.又∠AGE=∠DGF,∴∠AGD=∠EGF,∴△AGD∽△EGF.(7分)
(3)如图1,延长AD交GB于点M,交BC的延长线于点H,则AH⊥BH.
由△AGD≌△BGC,知∠GAD=∠GBC.
在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB.
∴∠AGB=∠AHB=90°,
∴∠AGE=∠AGB=45°,
∴=.
又△AGD∽△EGF,
∴==.(10分)
(本小题解法有多种,如可按图2和图3作辅助线求解,过程略)
29.
解:(1)把A(-1,0)、B(3,0),两点的坐标代入y=ax2+bx-3得:
解得:,
所以,这条抛物线的解析这式为:y=x2-2x-3;(3分)
(2)设点P的横坐标是m,则P(m,m2-2m-3),E(m,m-2)F(m,0),
PE=|yE-yP|=|(m-2)-(m2-2m-3)|=|-m2+3m+1|,
EF=|-m+2|,
由题意PE=3EF,即:|-m2+3m+1|=3|-m+2|,
①若-m2+3m+1=3(-m+2),
整理得:m2-6m+5=0,
解得:m=1或m=5,
∵P在x轴下方,
∴-1<m<3,
∴m=5不合题意应舍去,
∴m=1,
②若-m2+3m+1=-3(-m+2),
整理得:m2-7=0,
解得:m=或m=-,
∵P在x轴下方,
∴-1<m<3,m=-不合题意应舍去,
∴m=,
综上所述,m=1或m=;(8分)
(3)存在点P的横坐标为:m=1±,或或.
理由如下:直线y=x-2与y轴的夹角为45°,
①∠PCE=90°时,直线PC的解析式为y=-x-2,
联立,
消掉y得,x2-x-1=0,
解得或,
所以,点P的横坐标或;
②∠CPE=90°时,PC∥x轴,
∵点C(0,-2),
∴点P与点C的纵坐标相等,为-2,
∴x2-2x-3=-2,
解得x=1±,
综上所述,点P的横坐标m=1±,或或.(12分)
同课章节目录
