位似图形

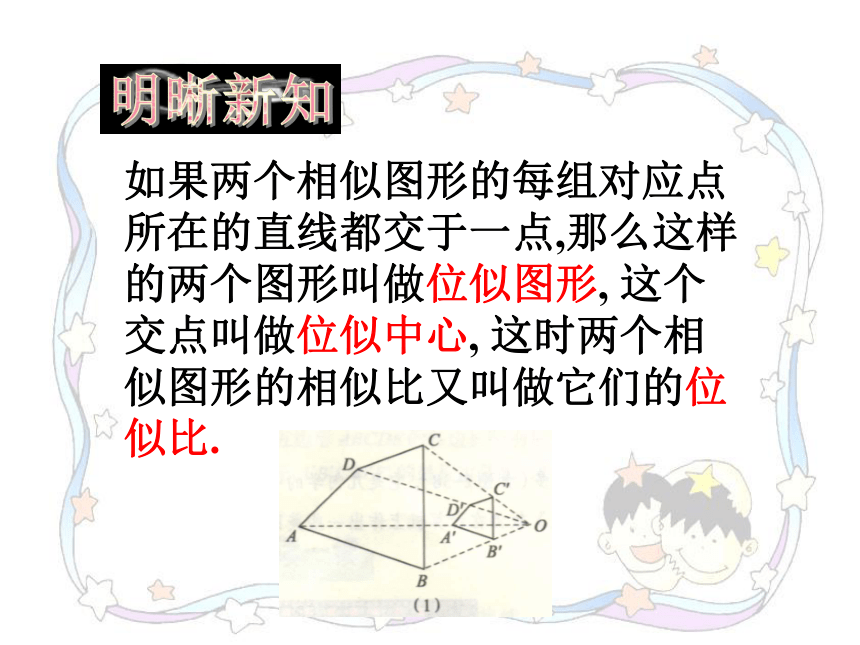
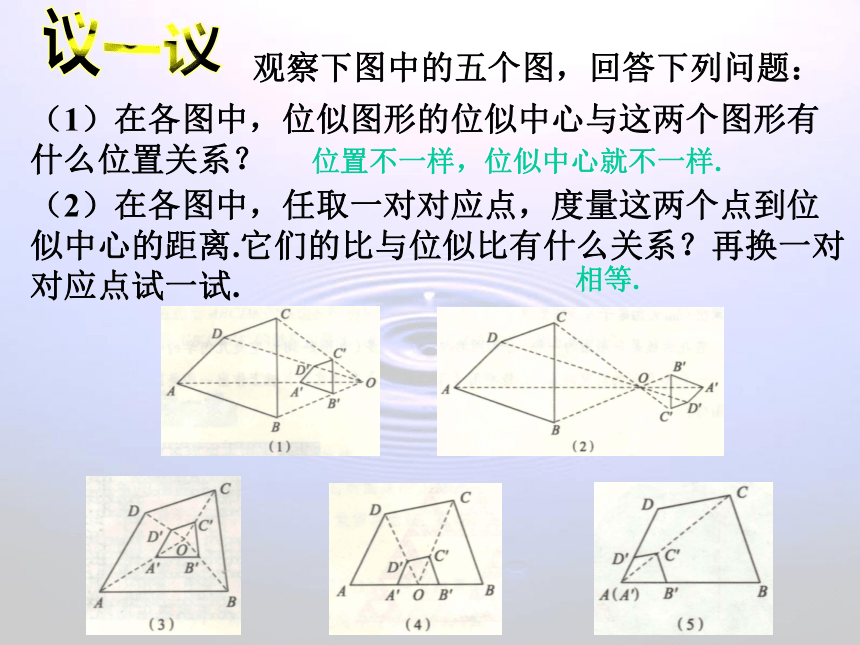
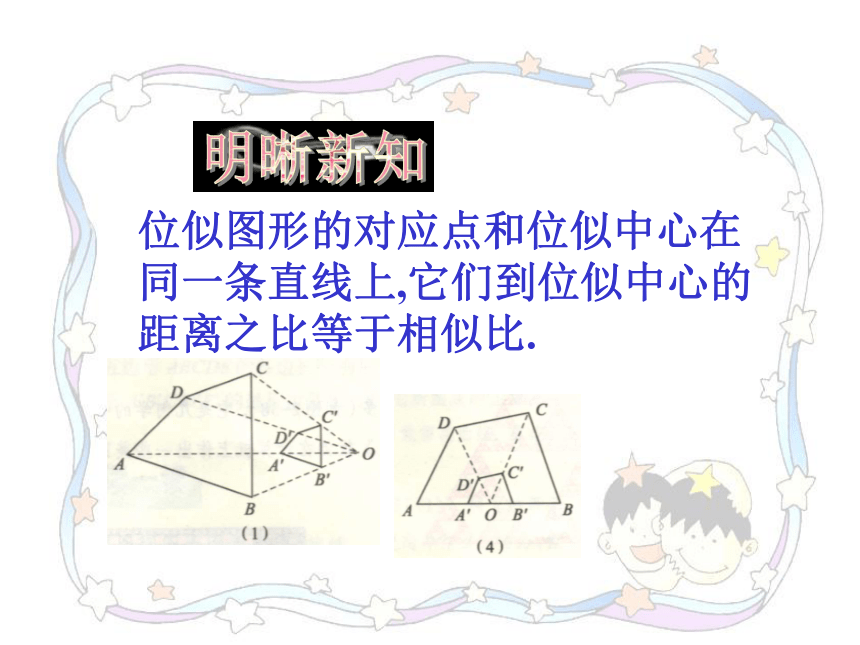
课件12张PPT。位似图形（1） 下列图形中，每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图，你发现每个图中的两个四边形各对应点的连线有什么特征？明晰新知如果两个相似图形的每组对应点所在的直线都交于一点,那么这样的两个图形叫做位似图形, 这个交点叫做位似中心, 这时两个相似图形的相似比又叫做它们的位似比.议一议观察下图中的五个图，回答下列问题：（1）在各图中，位似图形的位似中心与这两个图形有什么位置关系？（2）在各图中，任取一对对应点，度量这两个点到位似中心的距离.它们的比与位似比有什么关系？再换一对对应点试一试.位置不一样，位似中心就不一样.相等.明晰新知位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比.典例解析如图，D，E分别AB，AC上的点.（1）如果DE∥BC，那么?ADE和 ?ABC是位似图形吗？为什么？解：（1） ?ADE和 ?ABC是位似图形.理由是：因为DE∥BC，所以∠ADE和＝∠B， ∠AED ＝∠C.所以?ADE∽ ?ABC.又因为 点A是?ADE和 ?ABC的公共点，点D和点B是对应点，点E和点C是对应点，直线BD与CE交于点A，所以?ADE和 ?ABC是位似图形.典例解析如图，D，E分别AB，AC上的点.（1）如果DE∥BC，那么?ADE和 ?ABC是位似图形吗？为什么？（2）如果?ADE和 ?ABC是位似图形，那么DE∥BC吗？为什么？解：（2） DE∥BC.理由是：?ADE和 ?ABC是位似图形，?ADE∽ ?ABC∠ADE＝∠BDE∥BC.不经过位似中心的对应线段平行.在下列每个图形中，位似图形的对应线段AB与A′B′是否平行？BC与B′C′，CD与C′D′，AD与A′D′是否平行？为什么？ 随堂练习1.（1），（4）.2.是.习题 1、 2.如图,已知△ABC∽△DEF， 它们对应顶点的连线AD,BE,CF相交于点O,这两个三角形是不是位似三角形?0BECFAD通过这节课的学习，你有哪些收获？课堂小结1.如果两个相似图形的每组对应点所在的直线都交于一点,那么这样的两个图形叫做位似图形, 这个交点叫做位似中心, 这时两个相似图形的相似比又叫做它们的位似比.2.位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比.3.位似图形中不经过位似中心的对应线段平行.对自己本节课的学习情况进行评价.课堂小结1.如果两个相似图形的每组对应点所在的直线都交于一点,那么这样的两个图形叫做位似图形, 这个交点叫做位似中心, 这时两个相似图形的相似比又叫做它们的位似比.2.位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比.3.位似图形中不经过位似中心的对应线段平行.