2016年河北省中考数学备考课件(共78张PPT)
文档属性
| 名称 | 2016年河北省中考数学备考课件(共78张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-28 00:00:00 | ||
图片预览











文档简介
课件78张PPT。15年中考阅卷阅卷总结 选择题分析选择题的命制有如下特点:
1.试题起点较低,难度分布合理有序;
2.较好地考查了基本知识、基本技能、以及一些基本的数学思想方法;
3.试题的呈现方式上做到了“常考常新”。一些题目改编自课本例题和“考试说明”,或者是我们所见过的熟悉的背景,但是改编得都很精致,可以说是“熟悉的陌生题”;阅卷总结17.若|a|=20150,则a= .本题考察绝对值的定义和非零数的零次幂。 失分原因 : 1.忽略1的平方根是±1两个数。
2.部分考生认为20150=2015。
解法:本题解法单一,根据20150=1,得到a= ±1教学建议:重视基本概念,基础知识教学,夯实基础。阅卷总结 18.若x+y=1,且,则x≠0,则
的值为_____________.阅卷总结 若实数m,n满足|m-2|+(n-2014)2=0.则m-1+n0= 。 阅卷总结18.若a=2b≠0, 则 的值为 .
本题考察因式分解、分式化简及字母的代入消元。 失分原因 : 1.未化简直接代入消元,而计算过程比 化简后代入稍显复杂,导致计算错误发生。
2.结果未化简成最简形式,出现如 等结果。
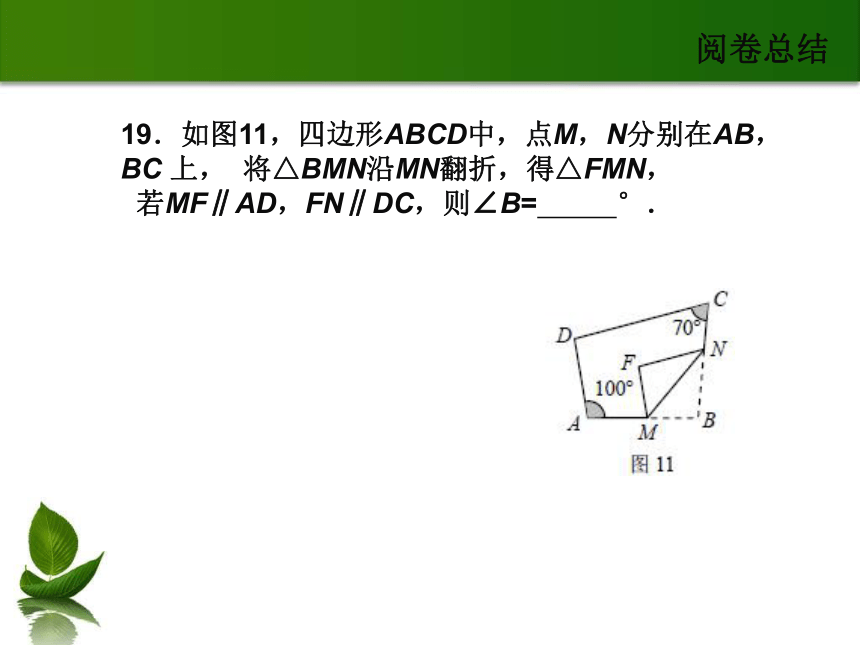
解法:18题解法教学建议:平时教学加强对运算能力的训练阅卷总结阅卷总结 19.如图11,四边形ABCD中,点M,N分别在AB,BC 上, 将△BMN沿MN翻折,得△FMN,
若MF∥AD,FN∥DC,则∠B= °.阅卷总结19题解法阅卷总结阅卷总结 20.如图12,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点 A1 旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;……如此进行下去,直至得C13.若P(37,m)在第13段抛物线C13上,则m =_________.
阅卷总结 20、如图,点O,A在数轴上表示的数分别是0, 0.1
将线段OA分成100等份,其分点由左向右依次为M1,M2……M99;
将线段O M1分成100等份,其分点由左向右依次为N1,N2……N99
将线段O N1分成100等份,其分点由左向右依次为P1,P2……P99
则点P1所表示的数用科学计数法表示为 。 20题阅卷总结20题 解法、教学建议阅卷总结21题阅卷总结21题 答题情况 ①阅卷总结21题 主要出错点 21题 题目评价阅卷总结21题 反馈教学阅卷总结22题阅卷总结22题 考核内容阅卷总结22题 学生大题情况阅卷总结22题 学生大题情况阅卷总结22题 学生大题情况阅卷总结22题失分原因 阅卷总结22题失分原因 阅卷总结22题 存在问题阅卷总结23题阅卷总结23题 考察内容阅卷总结23题 答题情况阅卷总结23题 对分原因阅卷总结23题 存在问题阅卷总结23题 多种解法阅卷总结23题 教学建议阅卷总结24题(11分)阅卷总结24题 考察内容阅卷总结24题 答题情况阅卷总结24题 存在问题阅卷总结24题 存在问题阅卷总结24题 解法阅卷总结24题 教学建议24题 教学建议25题25题 考察内容25题 得分情况25题 得分情况25题 正确解法25题 正确解法25题 正确解法25题 正确解法25题 正确解法25题 正确解法25题 典型错误25题 典型错误25题 失分原因25题 失分原因25题 教学建议 25题 教学建议 26题26题 评分标准26题 考察内容26题 答题情况26题 失分原因26题 多种解法26题 教学建议26题 拓展的评分标准 、考察内容26题拓展 答题情况26题拓展 失分原因、解法归纳26题拓展 教学建议26题探究 考察内容26题探究 答题情况26题探究 失分原因26题探究 解法归纳26题探究 解法归纳阅卷总结 定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如: 2⊕5=2?(2-5)+1
=2?(-3)+1
=-6+1
=-5.
(1)求(-2)⊕3的值
(2)若3⊕x的值小于13,求x的取值范围,并在图13所示的数轴上表示出来. 阅卷总结 某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图14-1)和条形图(如图14-2),经确认扇形图是正确的,而条形图尚有一处错误.
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数、中位数;
(3)在求这20名学生每人植树量的平均数时,
小宇是这样分析的:
① 小宇的分析是从哪一步开始出现错误的?
② 请你帮他计算出正确的平均数,并估计这260名
学生共植树多少棵. 阅卷总结 1. 在教学时,要注重基础,要保证学生的基础知识必须扎实。
2. 注重基本计算,包括代数式的化简、等式的变形等,为数学问题的解决提供最基本的保障.
3.利用实物或几何图形发展学生空间想象能力,并注重培养学生数形结合的思想.
4.在几何证明的教学过程中,加强推理证明的训练,使学生形成严谨的逻辑推理能力和思维方式;
5.建议对于变化的问题,教学时要注重培养学生从变化中寻找不变量的能力,利用不变量灵活解决问题.谢谢!
Thanks!
1.试题起点较低,难度分布合理有序;
2.较好地考查了基本知识、基本技能、以及一些基本的数学思想方法;
3.试题的呈现方式上做到了“常考常新”。一些题目改编自课本例题和“考试说明”,或者是我们所见过的熟悉的背景,但是改编得都很精致,可以说是“熟悉的陌生题”;阅卷总结17.若|a|=20150,则a= .本题考察绝对值的定义和非零数的零次幂。 失分原因 : 1.忽略1的平方根是±1两个数。
2.部分考生认为20150=2015。
解法:本题解法单一,根据20150=1,得到a= ±1教学建议:重视基本概念,基础知识教学,夯实基础。阅卷总结 18.若x+y=1,且,则x≠0,则
的值为_____________.阅卷总结 若实数m,n满足|m-2|+(n-2014)2=0.则m-1+n0= 。 阅卷总结18.若a=2b≠0, 则 的值为 .
本题考察因式分解、分式化简及字母的代入消元。 失分原因 : 1.未化简直接代入消元,而计算过程比 化简后代入稍显复杂,导致计算错误发生。
2.结果未化简成最简形式,出现如 等结果。
解法:18题解法教学建议:平时教学加强对运算能力的训练阅卷总结阅卷总结 19.如图11,四边形ABCD中,点M,N分别在AB,BC 上, 将△BMN沿MN翻折,得△FMN,
若MF∥AD,FN∥DC,则∠B= °.阅卷总结19题解法阅卷总结阅卷总结 20.如图12,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点 A1 旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;……如此进行下去,直至得C13.若P(37,m)在第13段抛物线C13上,则m =_________.
阅卷总结 20、如图,点O,A在数轴上表示的数分别是0, 0.1
将线段OA分成100等份,其分点由左向右依次为M1,M2……M99;
将线段O M1分成100等份,其分点由左向右依次为N1,N2……N99
将线段O N1分成100等份,其分点由左向右依次为P1,P2……P99
则点P1所表示的数用科学计数法表示为 。 20题阅卷总结20题 解法、教学建议阅卷总结21题阅卷总结21题 答题情况 ①阅卷总结21题 主要出错点 21题 题目评价阅卷总结21题 反馈教学阅卷总结22题阅卷总结22题 考核内容阅卷总结22题 学生大题情况阅卷总结22题 学生大题情况阅卷总结22题 学生大题情况阅卷总结22题失分原因 阅卷总结22题失分原因 阅卷总结22题 存在问题阅卷总结23题阅卷总结23题 考察内容阅卷总结23题 答题情况阅卷总结23题 对分原因阅卷总结23题 存在问题阅卷总结23题 多种解法阅卷总结23题 教学建议阅卷总结24题(11分)阅卷总结24题 考察内容阅卷总结24题 答题情况阅卷总结24题 存在问题阅卷总结24题 存在问题阅卷总结24题 解法阅卷总结24题 教学建议24题 教学建议25题25题 考察内容25题 得分情况25题 得分情况25题 正确解法25题 正确解法25题 正确解法25题 正确解法25题 正确解法25题 正确解法25题 典型错误25题 典型错误25题 失分原因25题 失分原因25题 教学建议 25题 教学建议 26题26题 评分标准26题 考察内容26题 答题情况26题 失分原因26题 多种解法26题 教学建议26题 拓展的评分标准 、考察内容26题拓展 答题情况26题拓展 失分原因、解法归纳26题拓展 教学建议26题探究 考察内容26题探究 答题情况26题探究 失分原因26题探究 解法归纳26题探究 解法归纳阅卷总结 定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如: 2⊕5=2?(2-5)+1
=2?(-3)+1
=-6+1
=-5.
(1)求(-2)⊕3的值
(2)若3⊕x的值小于13,求x的取值范围,并在图13所示的数轴上表示出来. 阅卷总结 某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图14-1)和条形图(如图14-2),经确认扇形图是正确的,而条形图尚有一处错误.
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数、中位数;
(3)在求这20名学生每人植树量的平均数时,
小宇是这样分析的:
① 小宇的分析是从哪一步开始出现错误的?
② 请你帮他计算出正确的平均数,并估计这260名
学生共植树多少棵. 阅卷总结 1. 在教学时,要注重基础,要保证学生的基础知识必须扎实。
2. 注重基本计算,包括代数式的化简、等式的变形等,为数学问题的解决提供最基本的保障.
3.利用实物或几何图形发展学生空间想象能力,并注重培养学生数形结合的思想.
4.在几何证明的教学过程中,加强推理证明的训练,使学生形成严谨的逻辑推理能力和思维方式;
5.建议对于变化的问题,教学时要注重培养学生从变化中寻找不变量的能力,利用不变量灵活解决问题.谢谢!
Thanks!
同课章节目录
