14.2 勾股定理的应用 同步练习(含答案)2024-2025学年华东师大版数学八年级上册
文档属性
| 名称 | 14.2 勾股定理的应用 同步练习(含答案)2024-2025学年华东师大版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 914.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-04 15:31:35 | ||
图片预览



文档简介
14.2 勾股定理的应用
一、单选题
1.如图,有两棵树,一棵高2米,另一棵高5.6米,两树相距4.8米,小成看到一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少要飞行( )米.
A.4.8 B.6 C.5.6 D.8
2.《九章算术》书上一个问题“今有垣高一丈.倚木于垣,上与垣齐.引木却行一尺,其木至地.问木长几何?”其内容表述为:“有一面墙,高1丈,将一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上.如果使木杆下端从此时的位置向远离墙的方向移动1尺,则木杆上端恰好沿着墙滑落到地面上.问木杆长多少尺?”(说明:1丈尺)设木杆长尺,依题意,下列方程正确的是( )
A. B. C. D.
3.如图,在四边形ABCD中,AD∥BC,∠C=90°,△BCD与△BC′D关于直线BD轴对称,BC=6,CD=3,点C与点C′对应,BC′交AD于点E,则线段DE的长为( )
A.3 B. C.5 D.
4.如图,这是一个供滑板爱好者使用的U型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为的半圆,其边缘,点E在上,,一滑板爱好者从A点滑到E点,则他滑行的最短距离为( )米.(边缘部分的厚度忽略不计)
A.25 B.24 C.26 D.
5.如图所示,圆柱底面半径为,高为,点,分别是圆柱两底面圆周上的点,且,在同一高线上,用一根棉线从点顺着圆柱侧面绕圈到点,则这根棉线的长度最短为( )
A. B. C. D.
6.一只的铅笔放在圆柱体笔筒中,笔筒内部底面直径是,内壁高,那么这根铅笔需在笔筒外的部分长度h的范围是( )
A. B. C. D.
7.如图,在离水面点A高度为的岸上点处,有人用绳子拉船靠岸,开始时绳子的长为,此人以的速度收绳,后船移动到点的位置,则船向岸边移动了( )(假设绳子是直的)
A. B. C. D.
8.如图,在灯塔O的北偏东方向处有一轮船A,在灯塔O的南偏东方向处有一渔船B,则A,B间的距离为( )
A. B. C. D.
9.古代数学名著《算法统宗》中有一首计算秋千绳索长度的问题:“平地秋千未起,踏板一尺离地.送行二步恰竿齐,五尺板高离地……”.翻译成现代文:如图,秋千静止的时候,踏板离地高一尺(尺),将它往前推进两步(尺),此时踏板升高离地五尺(尺),则秋千绳索(或)的长度为( )
A.13.5尺 B.14尺 C.14.5尺 D.15尺
10.如图,一个长方体工艺品的高为,底面是边长为的正方形.一只爬虫从底面顶点A沿该工艺品的表面爬向顶点B,那么它爬行的最短路程为( )
A. B. C. D.
二、填空题
11.《九章算术》是我因古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,中,,,,求的长,如果设,则可列方程为 .
12.如图,一条路的两边有两棵树,一棵树高为11米,另一棵树高为6米,两树的距离为12米.若一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少要飞行 米.
13.如图,某人欲垂直横渡一条河,由于水流的影响,他实际上岸地点C偏离了想要到达的B点(即),其结果是他在水中实际游了(即),则该河处的宽度是 .
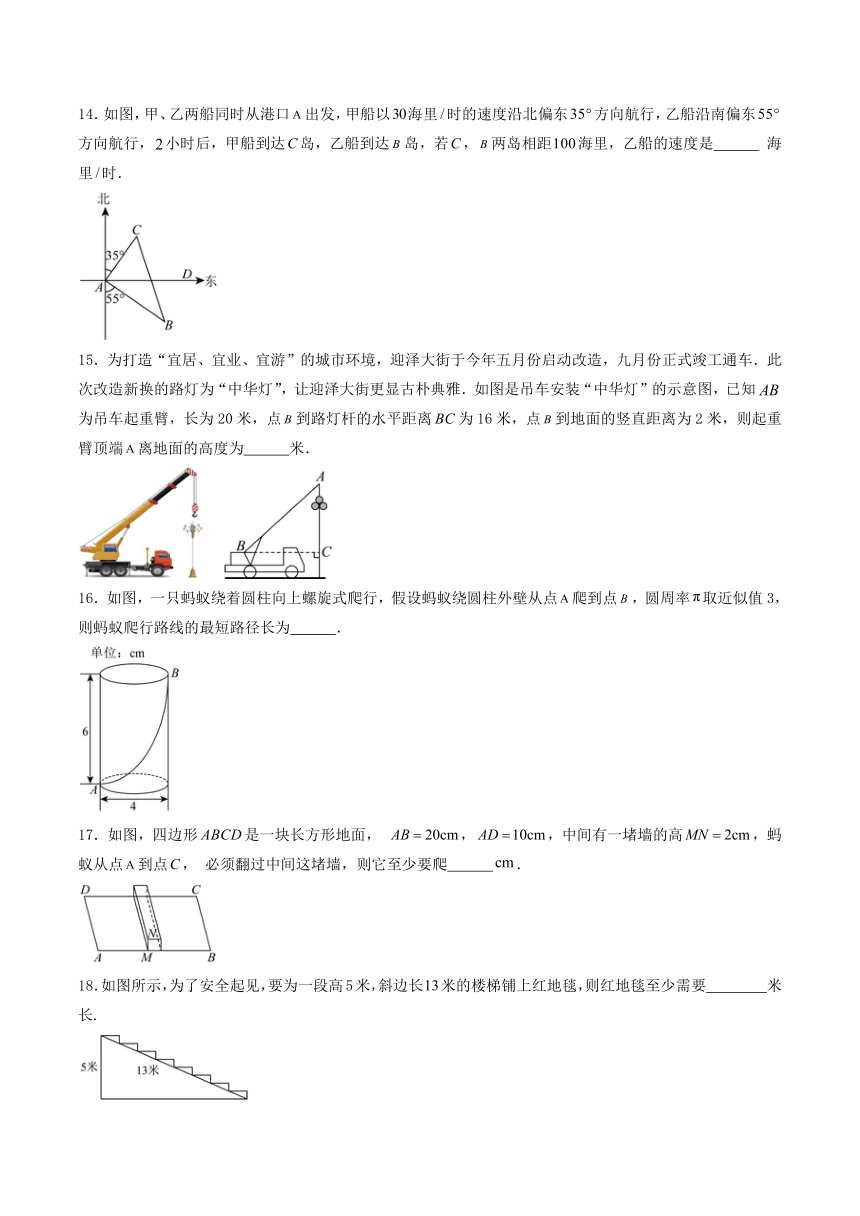
14.如图,甲、乙两船同时从港口出发,甲船以海里时的速度沿北偏东方向航行,乙船沿南偏东方向航行,小时后,甲船到达岛,乙船到达岛,若,两岛相距海里,乙船的速度是 海里时.
15.为打造“宜居、宜业、宜游”的城市环境,迎泽大街于今年五月份启动改造,九月份正式竣工通车.此次改造新换的路灯为“中华灯”,让迎泽大街更显古朴典雅.如图是吊车安装“中华灯”的示意图,已知为吊车起重臂,长为20米,点到路灯杆的水平距离为16米,点到地面的竖直距离为2米,则起重臂顶端离地面的高度为 米.
16.如图,一只蚂蚁绕着圆柱向上螺旋式爬行,假设蚂蚁绕圆柱外壁从点爬到点,圆周率取近似值3,则蚂蚁爬行路线的最短路径长为 .
17.如图,四边形是一块长方形地面, ,,中间有一堵墙的高,蚂蚁从点到点, 必须翻过中间这堵墙,则它至少要爬 .
18.如图所示,为了安全起见,要为一段高5米,斜边长米的楼梯铺上红地毯,则红地毯至少需要 米长.
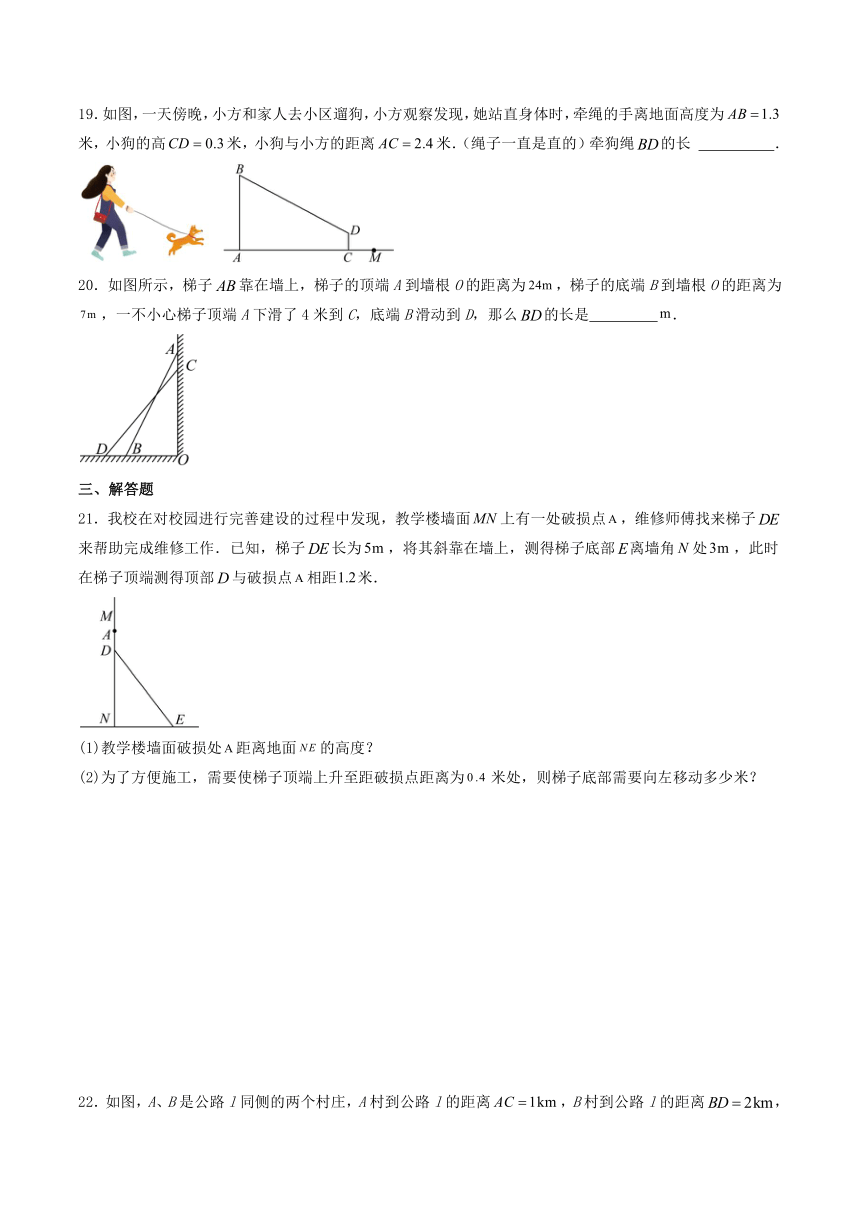
19.如图,一天傍晚,小方和家人去小区遛狗,小方观察发现,她站直身体时,牵绳的手离地面高度为米,小狗的高米,小狗与小方的距离米.(绳子一直是直的)牵狗绳的长 .
20.如图所示,梯子靠在墙上,梯子的顶端A到墙根O的距离为,梯子的底端B到墙根O的距离为,一不小心梯子顶端A下滑了4米到C,底端B滑动到D,那么的长是 .
三、解答题
21.我校在对校园进行完善建设的过程中发现,教学楼墙面上有一处破损点,维修师傅找来梯子来帮助完成维修工作.已知,梯子长为,将其斜靠在墙上,测得梯子底部离墙角处,此时在梯子顶端测得顶部与破损点相距米.
(1)教学楼墙面破损处距离地面的高度?
(2)为了方便施工,需要使梯子顶端上升至距破损点距离为米处,则梯子底部需要向左移动多少米?
22.如图,A、B是公路l同侧的两个村庄,A村到公路l的距离,B村到公路l的距离,且.为方便村民出行,计划在公路边新建一个公交站点P,要求该站到村庄A、B的距离相等.请求出点P与点C之间的距离.
23.物理课上,老师带着科技小组进行物理实验.同学们将一根不可拉伸的绳子绕过定滑轮,一端拴在滑块上,另一端拴在物体上,滑块放置在水平地面的直轨道上,通过滑块的左右滑动来调节物体的升降.
实验初始状态如图1所示,物体静止在直轨道上,物体到滑块的水平距离是6,物体到定滑轮的垂直距离是8.(实验过程中,绳子始终保持绷紧状态,定滑轮、滑块和物体的大小忽略不计.)
(1)求绳子的总长度;
(2)如图2,若物体升高7,求滑块向左滑动的距离.
24.森林火灾是一种常见的自然灾害,危害很大,随着中国科技、经济的不断发展,开始应用飞机洒水的方式扑灭火源.如图,有一台救火飞机沿东西方向,由点飞向点,已知点为其中一个着火点,已知,,,飞机中心周围以内可以受到洒水影响.
(1)在飞机飞行过程中,求飞机距离着火点的最短距离;
(2)若该飞机的速度为,要想扑灭着火点估计需要15秒,请你通过计算说明着火点能否被飞机扑灭.
25.如图是小明家中的三个房间甲、乙、丙的截面图,他将一个梯子斜靠在墙上,梯子顶端距离地面的垂直距离记作,如果梯子的底端不动,顶端靠在对面墙上,此时梯子的顶端距离地面的垂直距离记作.
(1)当小明在甲房间时,梯子靠在对面墙上,顶端刚好落在对面墙角处,若米,米,则甲房间的宽度 米.
(2)当他在乙房间时,测得米,米,且,求乙房间的宽;
(3)当他在丙房间时,测得米,且,,求丙房间的宽.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B A A A A B C C
11. 12.13 13.480 14.40 15.14
16. 17. 18. 19.2.6米 20.8
21.(1)解:由题意得,,,,
由勾股定理得:,
∴教学楼墙面破损处距离地面的高度,
答:教学楼墙面破损处距离地面的高度为;
(2)解:由题意得,梯子顶端离地面,
∴梯子底部离墙角处为,
∴梯子底部需要向左移动,
答:梯子底部需要向左移动.
22.解:设,则,
在中,,
在中,,
,
∴,
∴,解得,∴.
23.(1)解:由题意得6,.
∴,
∴,
即:绳子的总长度为
(2)解:如图所示:
由题意得,6,8.
∴,
∴,即:滑块向左滑动的距离为
24.(1)解:如图,过点作于点,
,,,
,,
,
是直角三角形,
,
,
因为飞机中心周围以内可以受到洒水影响,,
所以着火点受洒水影响;
(2)解:如图,当时,飞机正好喷到着火点,
,
在中,,
所以.
因为飞机的速度为,
所以,
20秒秒,
答:着火点能被扑灭.
25.(1)解:在中,,米,米,
,
,
甲房间的宽度米,
故答案为:3.2;
(2),
,
,
.
在△与△中,
,
△△,
米,
,
;
(3)过点作垂线,垂足点,连接.
设,且.
梯子的倾斜角为,
△为等腰直角三角形,△为等边三角形,梯子长度相同),.
,
.
,
△为等边三角形,
.
△△,
,
米,
即丙房间的宽是1.6米.
一、单选题
1.如图,有两棵树,一棵高2米,另一棵高5.6米,两树相距4.8米,小成看到一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少要飞行( )米.
A.4.8 B.6 C.5.6 D.8
2.《九章算术》书上一个问题“今有垣高一丈.倚木于垣,上与垣齐.引木却行一尺,其木至地.问木长几何?”其内容表述为:“有一面墙,高1丈,将一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上.如果使木杆下端从此时的位置向远离墙的方向移动1尺,则木杆上端恰好沿着墙滑落到地面上.问木杆长多少尺?”(说明:1丈尺)设木杆长尺,依题意,下列方程正确的是( )
A. B. C. D.
3.如图,在四边形ABCD中,AD∥BC,∠C=90°,△BCD与△BC′D关于直线BD轴对称,BC=6,CD=3,点C与点C′对应,BC′交AD于点E,则线段DE的长为( )
A.3 B. C.5 D.
4.如图,这是一个供滑板爱好者使用的U型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为的半圆,其边缘,点E在上,,一滑板爱好者从A点滑到E点,则他滑行的最短距离为( )米.(边缘部分的厚度忽略不计)
A.25 B.24 C.26 D.
5.如图所示,圆柱底面半径为,高为,点,分别是圆柱两底面圆周上的点,且,在同一高线上,用一根棉线从点顺着圆柱侧面绕圈到点,则这根棉线的长度最短为( )
A. B. C. D.
6.一只的铅笔放在圆柱体笔筒中,笔筒内部底面直径是,内壁高,那么这根铅笔需在笔筒外的部分长度h的范围是( )
A. B. C. D.
7.如图,在离水面点A高度为的岸上点处,有人用绳子拉船靠岸,开始时绳子的长为,此人以的速度收绳,后船移动到点的位置,则船向岸边移动了( )(假设绳子是直的)
A. B. C. D.
8.如图,在灯塔O的北偏东方向处有一轮船A,在灯塔O的南偏东方向处有一渔船B,则A,B间的距离为( )
A. B. C. D.
9.古代数学名著《算法统宗》中有一首计算秋千绳索长度的问题:“平地秋千未起,踏板一尺离地.送行二步恰竿齐,五尺板高离地……”.翻译成现代文:如图,秋千静止的时候,踏板离地高一尺(尺),将它往前推进两步(尺),此时踏板升高离地五尺(尺),则秋千绳索(或)的长度为( )
A.13.5尺 B.14尺 C.14.5尺 D.15尺
10.如图,一个长方体工艺品的高为,底面是边长为的正方形.一只爬虫从底面顶点A沿该工艺品的表面爬向顶点B,那么它爬行的最短路程为( )
A. B. C. D.
二、填空题
11.《九章算术》是我因古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,中,,,,求的长,如果设,则可列方程为 .
12.如图,一条路的两边有两棵树,一棵树高为11米,另一棵树高为6米,两树的距离为12米.若一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少要飞行 米.
13.如图,某人欲垂直横渡一条河,由于水流的影响,他实际上岸地点C偏离了想要到达的B点(即),其结果是他在水中实际游了(即),则该河处的宽度是 .
14.如图,甲、乙两船同时从港口出发,甲船以海里时的速度沿北偏东方向航行,乙船沿南偏东方向航行,小时后,甲船到达岛,乙船到达岛,若,两岛相距海里,乙船的速度是 海里时.
15.为打造“宜居、宜业、宜游”的城市环境,迎泽大街于今年五月份启动改造,九月份正式竣工通车.此次改造新换的路灯为“中华灯”,让迎泽大街更显古朴典雅.如图是吊车安装“中华灯”的示意图,已知为吊车起重臂,长为20米,点到路灯杆的水平距离为16米,点到地面的竖直距离为2米,则起重臂顶端离地面的高度为 米.
16.如图,一只蚂蚁绕着圆柱向上螺旋式爬行,假设蚂蚁绕圆柱外壁从点爬到点,圆周率取近似值3,则蚂蚁爬行路线的最短路径长为 .
17.如图,四边形是一块长方形地面, ,,中间有一堵墙的高,蚂蚁从点到点, 必须翻过中间这堵墙,则它至少要爬 .
18.如图所示,为了安全起见,要为一段高5米,斜边长米的楼梯铺上红地毯,则红地毯至少需要 米长.
19.如图,一天傍晚,小方和家人去小区遛狗,小方观察发现,她站直身体时,牵绳的手离地面高度为米,小狗的高米,小狗与小方的距离米.(绳子一直是直的)牵狗绳的长 .
20.如图所示,梯子靠在墙上,梯子的顶端A到墙根O的距离为,梯子的底端B到墙根O的距离为,一不小心梯子顶端A下滑了4米到C,底端B滑动到D,那么的长是 .
三、解答题
21.我校在对校园进行完善建设的过程中发现,教学楼墙面上有一处破损点,维修师傅找来梯子来帮助完成维修工作.已知,梯子长为,将其斜靠在墙上,测得梯子底部离墙角处,此时在梯子顶端测得顶部与破损点相距米.
(1)教学楼墙面破损处距离地面的高度?
(2)为了方便施工,需要使梯子顶端上升至距破损点距离为米处,则梯子底部需要向左移动多少米?
22.如图,A、B是公路l同侧的两个村庄,A村到公路l的距离,B村到公路l的距离,且.为方便村民出行,计划在公路边新建一个公交站点P,要求该站到村庄A、B的距离相等.请求出点P与点C之间的距离.
23.物理课上,老师带着科技小组进行物理实验.同学们将一根不可拉伸的绳子绕过定滑轮,一端拴在滑块上,另一端拴在物体上,滑块放置在水平地面的直轨道上,通过滑块的左右滑动来调节物体的升降.
实验初始状态如图1所示,物体静止在直轨道上,物体到滑块的水平距离是6,物体到定滑轮的垂直距离是8.(实验过程中,绳子始终保持绷紧状态,定滑轮、滑块和物体的大小忽略不计.)
(1)求绳子的总长度;
(2)如图2,若物体升高7,求滑块向左滑动的距离.
24.森林火灾是一种常见的自然灾害,危害很大,随着中国科技、经济的不断发展,开始应用飞机洒水的方式扑灭火源.如图,有一台救火飞机沿东西方向,由点飞向点,已知点为其中一个着火点,已知,,,飞机中心周围以内可以受到洒水影响.
(1)在飞机飞行过程中,求飞机距离着火点的最短距离;
(2)若该飞机的速度为,要想扑灭着火点估计需要15秒,请你通过计算说明着火点能否被飞机扑灭.
25.如图是小明家中的三个房间甲、乙、丙的截面图,他将一个梯子斜靠在墙上,梯子顶端距离地面的垂直距离记作,如果梯子的底端不动,顶端靠在对面墙上,此时梯子的顶端距离地面的垂直距离记作.
(1)当小明在甲房间时,梯子靠在对面墙上,顶端刚好落在对面墙角处,若米,米,则甲房间的宽度 米.
(2)当他在乙房间时,测得米,米,且,求乙房间的宽;
(3)当他在丙房间时,测得米,且,,求丙房间的宽.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B A A A A B C C
11. 12.13 13.480 14.40 15.14
16. 17. 18. 19.2.6米 20.8
21.(1)解:由题意得,,,,
由勾股定理得:,
∴教学楼墙面破损处距离地面的高度,
答:教学楼墙面破损处距离地面的高度为;
(2)解:由题意得,梯子顶端离地面,
∴梯子底部离墙角处为,
∴梯子底部需要向左移动,
答:梯子底部需要向左移动.
22.解:设,则,
在中,,
在中,,
,
∴,
∴,解得,∴.
23.(1)解:由题意得6,.
∴,
∴,
即:绳子的总长度为
(2)解:如图所示:
由题意得,6,8.
∴,
∴,即:滑块向左滑动的距离为
24.(1)解:如图,过点作于点,
,,,
,,
,
是直角三角形,
,
,
因为飞机中心周围以内可以受到洒水影响,,
所以着火点受洒水影响;
(2)解:如图,当时,飞机正好喷到着火点,
,
在中,,
所以.
因为飞机的速度为,
所以,
20秒秒,
答:着火点能被扑灭.
25.(1)解:在中,,米,米,
,
,
甲房间的宽度米,
故答案为:3.2;
(2),
,
,
.
在△与△中,
,
△△,
米,
,
;
(3)过点作垂线,垂足点,连接.
设,且.
梯子的倾斜角为,
△为等腰直角三角形,△为等边三角形,梯子长度相同),.
,
.
,
△为等边三角形,
.
△△,
,
米,
即丙房间的宽是1.6米.
