29.2直线与圆的位置关系 同步练习(含答案)2024-2025学年冀教版数学九年级下册
文档属性
| 名称 | 29.2直线与圆的位置关系 同步练习(含答案)2024-2025学年冀教版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 216.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
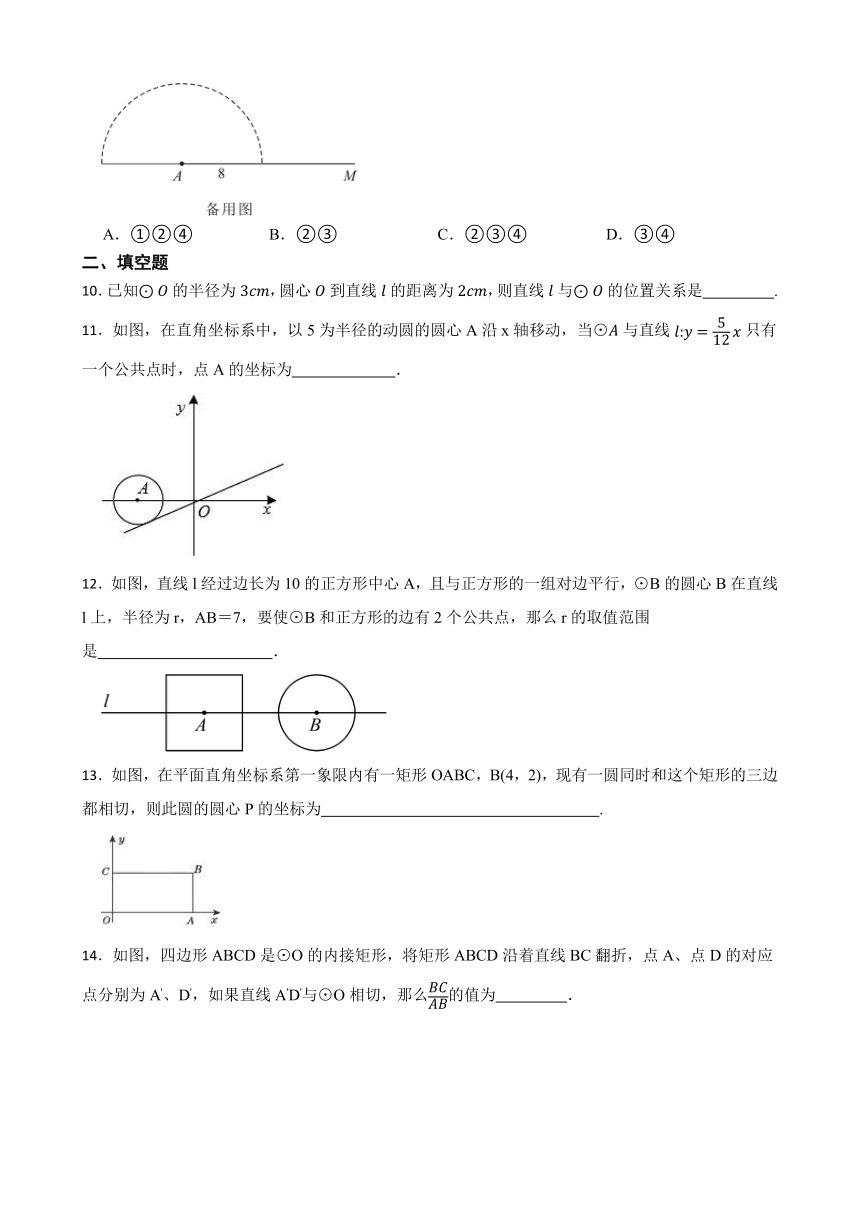
| 科目 | 数学 | ||
| 更新时间 | 2024-12-04 00:00:00 | ||
图片预览



文档简介
29.2 直线与圆的位置关系
一、选择题
1.在平面直角坐标系中,点M的坐标为(-2,3),以2为半径画⊙M,则下列结论中正确的是( )
A.⊙M与x轴相交,与y轴相切 B.⊙M与x轴相切,与y轴相离
C.⊙M与x轴相离,与y轴相交 D.⊙M与x轴相离,与y轴相切
2.已知的半径等于,圆心到直线上某点的距离为,则直线与的公共点的个数为( )
A.0 B.1 C.1或2 D.0或1
3.已知点A在半径为3的圆O上,如果点A到直线的距离是6,那么圆O与直线的位置关系是( )
A.相交 B.相离
C.相切 D.以上答案都不对
4.如图,平面直角坐标系中,经过三点,点D 是上的一动点.当点 D 到弦的距离最大时,点D 的坐标是( )
A. B. C. D.
5.在平面直角坐标系中,的半径是2,点在y轴上移动,当与x轴相交时,m的取值范围是( )
A. B.
C.或 D.
6.如图,在平面直角坐标系中,半径为2的圆心坐标是,将沿x轴正方向平移,使与y轴相切,则平移的距离为( )
A.1 B.1或5 C.3 D.5
7.如图,等边△ABC的周长为16π,半径是2的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( )
A.3周 B.4周 C.5周 D.6周
8.如图,已知Rt△ABC,AC=8,AB=4,以点B为圆心作圆,当⊙B与线段AC只有一个交点时,则⊙B的半径的取值范围是( )
A.rB = B.4 < rB ≤
C.rB = 或4 < rB ≤ D.rB为任意实数
9.程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题.操作学具时,点在轨道槽上运动,点既能在以为圆心、以为半径的半圆轨道槽上运动,也能在轨道槽上运动.图2是操作学具时,所对应某个位置的图形的示意图.
有以下结论:
①当时,可得到形状唯一确定的;
②当时,可得到形状唯一确定的;
③当时,可得到形状唯一确定的;
④当时,可得到形状唯一确定的;
其中所有正确结论的序号是( )
A.①②④ B.②③ C.②③④ D.③④
二、填空题
10.已知的半径为,圆心到直线的距离为,则直线与的位置关系是 .
11.如图,在直角坐标系中,以5为半径的动圆的圆心A沿x轴移动,当⊙与直线只有一个公共点时,点A的坐标为 .
12.如图,直线l经过边长为10的正方形中心A,且与正方形的一组对边平行,⊙B的圆心B在直线l上,半径为r,AB=7,要使⊙B和正方形的边有2个公共点,那么r的取值范围是 .
13.如图,在平面直角坐标系第一象限内有一矩形OABC,B(4,2),现有一圆同时和这个矩形的三边都相切,则此圆的圆心P的坐标为 .
14.如图,四边形ABCD是⊙O的内接矩形,将矩形ABCD沿着直线BC翻折,点A、点D的对应点分别为A'、D',如果直线A'D'与⊙O相切,那么的值为 .
15.如图,已知直线l:y=﹣ x﹣ 以每秒3个单位的速度向右平移;同时以点M(3,3)为圆心,3个单位长度为半径的⊙M以每秒2个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为 秒.
三、解答题
16.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,试判断半径为3的圆与OA的位置关系.
17.已知点O为坐标原点,点A的坐标为(2,3),⊙A的半径为1.过点A作直线l平行于x轴,点P在l上运动.
(1)当点P运动到圆上时,求线段OP的长.
(2)当点P的坐标为(4,3)时,试判断直线OP与⊙A的位置关系,并说明理由.
18.如图,已知Rt△ABC的斜边.
(1)以点为圆心作圆.当半径为多长时,AB与相切
(2)以点为圆心,分别以和长为半径作两个圆,这两个圆与AB分别有怎样的位置关系
19.设⊙O的圆心O到直线的距离为d,半径为r,且直线与⊙O相切.d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,求m的值.
20.如图,公路MN与公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m.假设拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否受到噪音影响?说明理由;如果受影响,且知拖拉机的速度为18km/h,那么学校受影响的时间是多少秒?
答案
1.D
2.C
3.D
4.A
5.D
6.B
7.C
8.C
9.C
10.相交
11.
12.2<r<12或r=13.
13.(1,1)或(3,1)或(2,0)或(2,2)
14.
15.2.5或10
16.解:过点C作CD⊥AO于点D,
∵∠O=30°,OC=6,
∴DC=3,
∴以点C为圆心,半径为3的圆与OA的位置关系是:相切.
17.(1)解:如图,设与轴的交点为,当点运动到圆上时,有点两个位置.
此时OP的长为或;
(2)解:相离.理由如下:
如图,过点作,垂足为.
在Rt中,.
,
.
,即,
直线OP与相离.
18.(1)解:过点C作CD⊥AB于点D,如图,
∵ 斜边AB=8cm,AC=4cm,
∴ BC=cm,
∴AC·BC=AB·CD,即×4×=×8×CD,
∴ CD=,即当半径为时, AB与相切;
(2)解:∵ 2cm<,
∴ 该圆与AB相离;
∵ 4cm>,
∴ 该圆与AB相交.
19.解: ∵⊙O的圆心O到直线的距离为d,半径为r,且直线与⊙O相切,
∴d=r,
∵d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,
∴△=0,
即[-(m+6)]2-4(m+9) 1=0,
解得:m=0或-8.
20.解:学校受到噪音影响.理由如下:
作AH⊥MN于H,如图,
∵PA=160m,∠QPN=30°,
∴AH=PA=80m,
而80m<100m,
∴拖拉机在公路MN上沿PN方向行驶时,学校受到噪音影响,
以点A为圆心,100m为半径作⊙A交MN于B、C,如图,
∵AH⊥BC,
∴BH=CH,
在Rt△ABH中,AB=100m,AH=80m,
BH==60m,
∴BC=2BH=120m,
∵拖拉机的速度=18km/h=5m/s,
∴拖拉机在线段BC上行驶所需要的时间==24(秒),
∴学校受影响的时间为24秒.
一、选择题
1.在平面直角坐标系中,点M的坐标为(-2,3),以2为半径画⊙M,则下列结论中正确的是( )
A.⊙M与x轴相交,与y轴相切 B.⊙M与x轴相切,与y轴相离
C.⊙M与x轴相离,与y轴相交 D.⊙M与x轴相离,与y轴相切
2.已知的半径等于,圆心到直线上某点的距离为,则直线与的公共点的个数为( )
A.0 B.1 C.1或2 D.0或1
3.已知点A在半径为3的圆O上,如果点A到直线的距离是6,那么圆O与直线的位置关系是( )
A.相交 B.相离
C.相切 D.以上答案都不对
4.如图,平面直角坐标系中,经过三点,点D 是上的一动点.当点 D 到弦的距离最大时,点D 的坐标是( )
A. B. C. D.
5.在平面直角坐标系中,的半径是2,点在y轴上移动,当与x轴相交时,m的取值范围是( )
A. B.
C.或 D.
6.如图,在平面直角坐标系中,半径为2的圆心坐标是,将沿x轴正方向平移,使与y轴相切,则平移的距离为( )
A.1 B.1或5 C.3 D.5
7.如图,等边△ABC的周长为16π,半径是2的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( )
A.3周 B.4周 C.5周 D.6周
8.如图,已知Rt△ABC,AC=8,AB=4,以点B为圆心作圆,当⊙B与线段AC只有一个交点时,则⊙B的半径的取值范围是( )
A.rB = B.4 < rB ≤
C.rB = 或4 < rB ≤ D.rB为任意实数
9.程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题.操作学具时,点在轨道槽上运动,点既能在以为圆心、以为半径的半圆轨道槽上运动,也能在轨道槽上运动.图2是操作学具时,所对应某个位置的图形的示意图.
有以下结论:
①当时,可得到形状唯一确定的;
②当时,可得到形状唯一确定的;
③当时,可得到形状唯一确定的;
④当时,可得到形状唯一确定的;
其中所有正确结论的序号是( )
A.①②④ B.②③ C.②③④ D.③④
二、填空题
10.已知的半径为,圆心到直线的距离为,则直线与的位置关系是 .
11.如图,在直角坐标系中,以5为半径的动圆的圆心A沿x轴移动,当⊙与直线只有一个公共点时,点A的坐标为 .
12.如图,直线l经过边长为10的正方形中心A,且与正方形的一组对边平行,⊙B的圆心B在直线l上,半径为r,AB=7,要使⊙B和正方形的边有2个公共点,那么r的取值范围是 .
13.如图,在平面直角坐标系第一象限内有一矩形OABC,B(4,2),现有一圆同时和这个矩形的三边都相切,则此圆的圆心P的坐标为 .
14.如图,四边形ABCD是⊙O的内接矩形,将矩形ABCD沿着直线BC翻折,点A、点D的对应点分别为A'、D',如果直线A'D'与⊙O相切,那么的值为 .
15.如图,已知直线l:y=﹣ x﹣ 以每秒3个单位的速度向右平移;同时以点M(3,3)为圆心,3个单位长度为半径的⊙M以每秒2个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为 秒.
三、解答题
16.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,试判断半径为3的圆与OA的位置关系.
17.已知点O为坐标原点,点A的坐标为(2,3),⊙A的半径为1.过点A作直线l平行于x轴,点P在l上运动.
(1)当点P运动到圆上时,求线段OP的长.
(2)当点P的坐标为(4,3)时,试判断直线OP与⊙A的位置关系,并说明理由.
18.如图,已知Rt△ABC的斜边.
(1)以点为圆心作圆.当半径为多长时,AB与相切
(2)以点为圆心,分别以和长为半径作两个圆,这两个圆与AB分别有怎样的位置关系
19.设⊙O的圆心O到直线的距离为d,半径为r,且直线与⊙O相切.d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,求m的值.
20.如图,公路MN与公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m.假设拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否受到噪音影响?说明理由;如果受影响,且知拖拉机的速度为18km/h,那么学校受影响的时间是多少秒?
答案
1.D
2.C
3.D
4.A
5.D
6.B
7.C
8.C
9.C
10.相交
11.
12.2<r<12或r=13.
13.(1,1)或(3,1)或(2,0)或(2,2)
14.
15.2.5或10
16.解:过点C作CD⊥AO于点D,
∵∠O=30°,OC=6,
∴DC=3,
∴以点C为圆心,半径为3的圆与OA的位置关系是:相切.
17.(1)解:如图,设与轴的交点为,当点运动到圆上时,有点两个位置.
此时OP的长为或;
(2)解:相离.理由如下:
如图,过点作,垂足为.
在Rt中,.
,
.
,即,
直线OP与相离.
18.(1)解:过点C作CD⊥AB于点D,如图,
∵ 斜边AB=8cm,AC=4cm,
∴ BC=cm,
∴AC·BC=AB·CD,即×4×=×8×CD,
∴ CD=,即当半径为时, AB与相切;
(2)解:∵ 2cm<,
∴ 该圆与AB相离;
∵ 4cm>,
∴ 该圆与AB相交.
19.解: ∵⊙O的圆心O到直线的距离为d,半径为r,且直线与⊙O相切,
∴d=r,
∵d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,
∴△=0,
即[-(m+6)]2-4(m+9) 1=0,
解得:m=0或-8.
20.解:学校受到噪音影响.理由如下:
作AH⊥MN于H,如图,
∵PA=160m,∠QPN=30°,
∴AH=PA=80m,
而80m<100m,
∴拖拉机在公路MN上沿PN方向行驶时,学校受到噪音影响,
以点A为圆心,100m为半径作⊙A交MN于B、C,如图,
∵AH⊥BC,
∴BH=CH,
在Rt△ABH中,AB=100m,AH=80m,
BH==60m,
∴BC=2BH=120m,
∵拖拉机的速度=18km/h=5m/s,
∴拖拉机在线段BC上行驶所需要的时间==24(秒),
∴学校受影响的时间为24秒.
