29.3切线的性质和判定 同步练习(含答案)2024-2025学年冀教版数学九年级下册
文档属性
| 名称 | 29.3切线的性质和判定 同步练习(含答案)2024-2025学年冀教版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 170.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-04 15:36:35 | ||
图片预览



文档简介
29.3 切线的性质和判定
一、选择题
1.下列直线是圆的切线的是( )
A.与圆有公共点的直线 B.到圆心的距离等于半径的直线
C.垂直于圆的半径的直线 D.过圆直径外端点的直线
2.如图,△ABC是☉O的内接三角形,下列选项中,能使过点A的直线EF与☉O相切于点A的条件是( )
A.∠EAB=∠C B.∠B=90°
C.EF⊥AC D.AC是☉O的直径
3.如图,AB与⊙O相切于点B,连结AO并延长交⊙O于点C,连结BC.若∠C=34°,则∠A的度数是( )
A.17° B.22° C.34° D.56°
4.平面直角坐标系中,点A(3,4),以点A为圆心,5为半径的圆与直线y=-x的位置关系是( )
A.相离 B.相切
C.相交 D.以上都有可能
5.如图,是的切线,为切点,交于点,若,,则的长为( )
A.5 B.7 C.8 D.13
6.如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+8上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A.2 B.4 C.8-2 D.2
7.如图,在足球比赛中,运动员甲从本方后场D处沿着垂直于对方球门线的方向带球前进,,垂足为C,若米,米,若仅从射门角度大小考虑(射门角度越大越容易进球),则甲位于最佳射门位置时离点C的距离为( )
A.4米 B.米 C.米 D.5米
8.一根钢管放在V形架内,其横截面如图所示,钢管的半径是12cm,若,则劣弧AB的长是( )
A.cm B.cm C.cm D.cm
9.已知P是上一点,用直尺和圆规过点P作一条直线,使它与相切于点 P.以下是甲、乙二人的作法.下列判断正确的是( )
甲:如图1,①连接,以点P 为圆心,长为半径画弧交于点A,连接并延长;②在上截取,直线即为所求. 乙:如图2,①作射线; ②在直线外任取一点A,以点A为圆心,长为半径作,与射线交于另一点B;③连接并延长与交于点C,直线即为所求.
A.甲、乙都正确 B.甲、乙都不正确
C.甲正确,乙不正确 D.甲不正确,乙正确
10.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A.点(0,3) B.点(1,3) C.点(6,0) D.点(6,1)
11.如图所示,已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是( )
A.OP=5 B.OE=OF
C.点O到直线EF的距离是4 D.OP⊥EF
12.如图,点A,B,D在☉O上,∠A=25°,OD的延长线交直线BC于点C,当∠OCB=( )时,直线BC与☉O相切.
A.25° B.40° C.50° D.60°
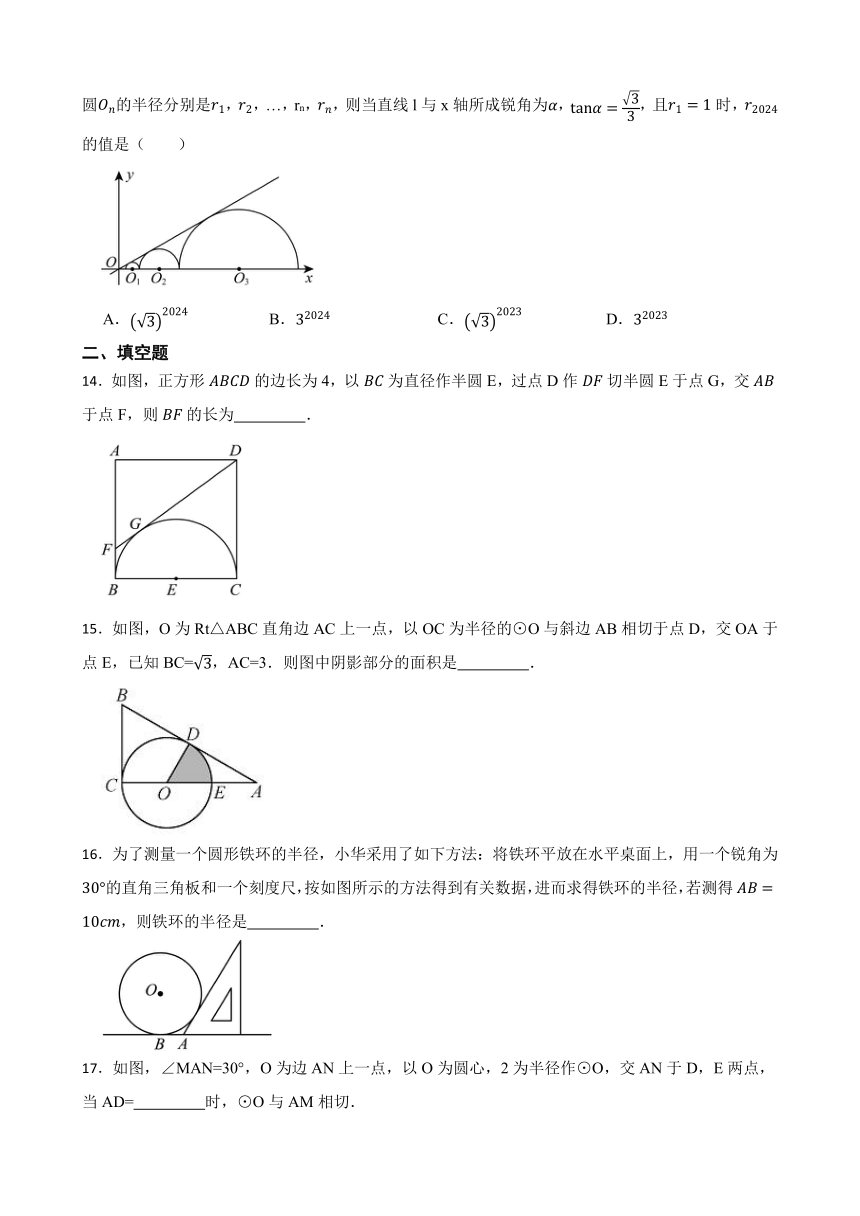
13.如图,圆心都在x轴正半轴上的半圆,半圆,…,半圆与直线l相切.设半圆,半圆,…,圆的半径分别是,,…,rn,,则当直线l与x轴所成锐角为,,且时,的值是( )
A. B. C. D.
二、填空题
14.如图,正方形的边长为4,以为直径作半圆E,过点D作切半圆E于点G,交于点F,则的长为 .
15.如图,O为Rt△ABC直角边AC上一点,以OC为半径的⊙O与斜边AB相切于点D,交OA于点E,已知BC=,AC=3.则图中阴影部分的面积是 .
16.为了测量一个圆形铁环的半径,小华采用了如下方法:将铁环平放在水平桌面上,用一个锐角为的直角三角板和一个刻度尺,按如图所示的方法得到有关数据,进而求得铁环的半径,若测得,则铁环的半径是 .
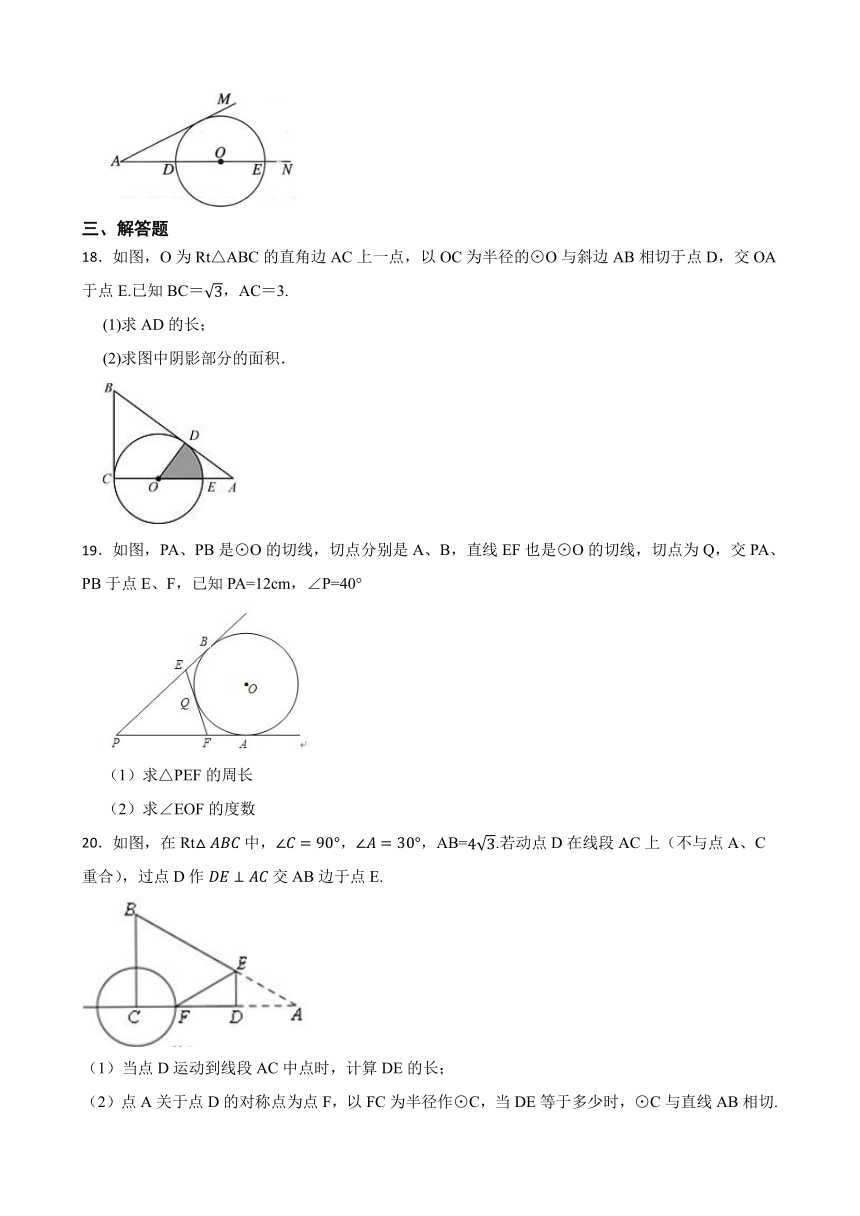
17.如图,∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,当AD= 时,⊙O与AM相切.
三、解答题
18.如图,O为Rt△ABC的直角边AC上一点,以OC为半径的⊙O与斜边AB相切于点D,交OA于点E.已知BC=,AC=3.
(1)求AD的长;
(2)求图中阴影部分的面积.
19.如图,PA、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为Q,交PA、PB于点E、F,已知PA=12cm,∠P=40°
(1)求△PEF的周长
(2)求∠EOF的度数
20.如图,在Rt中,,,AB=.若动点D在线段AC上(不与点A、C重合),过点D作交AB边于点E.
(1)当点D运动到线段AC中点时,计算DE的长;
(2)点A关于点D的对称点为点F,以FC为半径作⊙C,当DE等于多少时,⊙C与直线AB相切.
21.如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.
(1)AD是⊙O的切线吗?为什么?
(2)若OD⊥AB,BC=5,求⊙O的半径.
答案
1.B
2.A
3.B
4.C
5.C
6.A
7.B
8.A
9.A
10.B
11.D
12.B
13.D
14.1
15..
16.
17.2
18.(1)(2)
19.(1)解:
∵PA、PB是⊙O的切线,
∴PA=PB,
又∵直线EF是⊙O的切线,
∴EB=EQ,FQ=FA,
∴△PEF的周长=PE+PF+EF=PE+PF+EB+FA=PA+PB=2PA=24cm
(2)解:
连接OE,OF,则OE平分∠BEF,OF平分∠AFE,
则∠OEF+∠OFE=(∠P+∠PFE)+∠(P+∠PEF)= (180°+40°)=110°,
∴∠EOF=180°﹣110°=70°.
20.解:(1)∵∠C=90°,∠A=30°,AB=4,
∴BC=AB=2,AC=6,
∵∠C=90°,DE⊥AC,
∴DE∥BC,
∵D为AC中点,
∴E为AB中点,
∴DE=BC=,
(2)过C作CH⊥AB于H,
∵∠ACB=90°,BC=2,AB=4,AC=6,
∴由三角形面积公式得: BC AC=AB CH,CH=3,分为两种情况:①如图1,
∵CF=CH=3,
∴AF=6-3=3,
∵A和F关于D对称,
∴DF=AD=,
∵DE∥BC,
∴△ADE∽△ACB,
∴,
∴,DE=;
②如图2,
∵CF=CH=3,
∴AF=6+3=9,
∵A和F关于D对称,
∴DF=AD=4.5,
∵DE∥BC,
∴△ADE∽△ACB,
∴,
∴,
DE=.
21.解:(1)AD是⊙O的切线,理由如下:连接OA,
∵∠B=30°,
∴∠O=60°,
∵OA=OC,
∴∠OAC=60°,
∵∠CAD=30°,
∴∠OAD=90°,
又∴点A在⊙O 上,
∴AD是⊙O的切线;
(2)∵∠OAC=∠O=60°,
∴∠OCA=60°,
∴△AOC是等边三角形,
∵OD⊥AB,
∴OD垂直平分AB,
∴AC=BC=5,
∴OA=5,
即⊙O的半径为5.
一、选择题
1.下列直线是圆的切线的是( )
A.与圆有公共点的直线 B.到圆心的距离等于半径的直线
C.垂直于圆的半径的直线 D.过圆直径外端点的直线
2.如图,△ABC是☉O的内接三角形,下列选项中,能使过点A的直线EF与☉O相切于点A的条件是( )
A.∠EAB=∠C B.∠B=90°
C.EF⊥AC D.AC是☉O的直径
3.如图,AB与⊙O相切于点B,连结AO并延长交⊙O于点C,连结BC.若∠C=34°,则∠A的度数是( )
A.17° B.22° C.34° D.56°
4.平面直角坐标系中,点A(3,4),以点A为圆心,5为半径的圆与直线y=-x的位置关系是( )
A.相离 B.相切
C.相交 D.以上都有可能
5.如图,是的切线,为切点,交于点,若,,则的长为( )
A.5 B.7 C.8 D.13
6.如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+8上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A.2 B.4 C.8-2 D.2
7.如图,在足球比赛中,运动员甲从本方后场D处沿着垂直于对方球门线的方向带球前进,,垂足为C,若米,米,若仅从射门角度大小考虑(射门角度越大越容易进球),则甲位于最佳射门位置时离点C的距离为( )
A.4米 B.米 C.米 D.5米
8.一根钢管放在V形架内,其横截面如图所示,钢管的半径是12cm,若,则劣弧AB的长是( )
A.cm B.cm C.cm D.cm
9.已知P是上一点,用直尺和圆规过点P作一条直线,使它与相切于点 P.以下是甲、乙二人的作法.下列判断正确的是( )
甲:如图1,①连接,以点P 为圆心,长为半径画弧交于点A,连接并延长;②在上截取,直线即为所求. 乙:如图2,①作射线; ②在直线外任取一点A,以点A为圆心,长为半径作,与射线交于另一点B;③连接并延长与交于点C,直线即为所求.
A.甲、乙都正确 B.甲、乙都不正确
C.甲正确,乙不正确 D.甲不正确,乙正确
10.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A.点(0,3) B.点(1,3) C.点(6,0) D.点(6,1)
11.如图所示,已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是( )
A.OP=5 B.OE=OF
C.点O到直线EF的距离是4 D.OP⊥EF
12.如图,点A,B,D在☉O上,∠A=25°,OD的延长线交直线BC于点C,当∠OCB=( )时,直线BC与☉O相切.
A.25° B.40° C.50° D.60°
13.如图,圆心都在x轴正半轴上的半圆,半圆,…,半圆与直线l相切.设半圆,半圆,…,圆的半径分别是,,…,rn,,则当直线l与x轴所成锐角为,,且时,的值是( )
A. B. C. D.
二、填空题
14.如图,正方形的边长为4,以为直径作半圆E,过点D作切半圆E于点G,交于点F,则的长为 .
15.如图,O为Rt△ABC直角边AC上一点,以OC为半径的⊙O与斜边AB相切于点D,交OA于点E,已知BC=,AC=3.则图中阴影部分的面积是 .
16.为了测量一个圆形铁环的半径,小华采用了如下方法:将铁环平放在水平桌面上,用一个锐角为的直角三角板和一个刻度尺,按如图所示的方法得到有关数据,进而求得铁环的半径,若测得,则铁环的半径是 .
17.如图,∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,当AD= 时,⊙O与AM相切.
三、解答题
18.如图,O为Rt△ABC的直角边AC上一点,以OC为半径的⊙O与斜边AB相切于点D,交OA于点E.已知BC=,AC=3.
(1)求AD的长;
(2)求图中阴影部分的面积.
19.如图,PA、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为Q,交PA、PB于点E、F,已知PA=12cm,∠P=40°
(1)求△PEF的周长
(2)求∠EOF的度数
20.如图,在Rt中,,,AB=.若动点D在线段AC上(不与点A、C重合),过点D作交AB边于点E.
(1)当点D运动到线段AC中点时,计算DE的长;
(2)点A关于点D的对称点为点F,以FC为半径作⊙C,当DE等于多少时,⊙C与直线AB相切.
21.如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.
(1)AD是⊙O的切线吗?为什么?
(2)若OD⊥AB,BC=5,求⊙O的半径.
答案
1.B
2.A
3.B
4.C
5.C
6.A
7.B
8.A
9.A
10.B
11.D
12.B
13.D
14.1
15..
16.
17.2
18.(1)(2)
19.(1)解:
∵PA、PB是⊙O的切线,
∴PA=PB,
又∵直线EF是⊙O的切线,
∴EB=EQ,FQ=FA,
∴△PEF的周长=PE+PF+EF=PE+PF+EB+FA=PA+PB=2PA=24cm
(2)解:
连接OE,OF,则OE平分∠BEF,OF平分∠AFE,
则∠OEF+∠OFE=(∠P+∠PFE)+∠(P+∠PEF)= (180°+40°)=110°,
∴∠EOF=180°﹣110°=70°.
20.解:(1)∵∠C=90°,∠A=30°,AB=4,
∴BC=AB=2,AC=6,
∵∠C=90°,DE⊥AC,
∴DE∥BC,
∵D为AC中点,
∴E为AB中点,
∴DE=BC=,
(2)过C作CH⊥AB于H,
∵∠ACB=90°,BC=2,AB=4,AC=6,
∴由三角形面积公式得: BC AC=AB CH,CH=3,分为两种情况:①如图1,
∵CF=CH=3,
∴AF=6-3=3,
∵A和F关于D对称,
∴DF=AD=,
∵DE∥BC,
∴△ADE∽△ACB,
∴,
∴,DE=;
②如图2,
∵CF=CH=3,
∴AF=6+3=9,
∵A和F关于D对称,
∴DF=AD=4.5,
∵DE∥BC,
∴△ADE∽△ACB,
∴,
∴,
DE=.
21.解:(1)AD是⊙O的切线,理由如下:连接OA,
∵∠B=30°,
∴∠O=60°,
∵OA=OC,
∴∠OAC=60°,
∵∠CAD=30°,
∴∠OAD=90°,
又∴点A在⊙O 上,
∴AD是⊙O的切线;
(2)∵∠OAC=∠O=60°,
∴∠OCA=60°,
∴△AOC是等边三角形,
∵OD⊥AB,
∴OD垂直平分AB,
∴AC=BC=5,
∴OA=5,
即⊙O的半径为5.
