29.5 正多边形与圆 同步练习(含答案) 2024--2025学年冀教版九年级数学下册
文档属性
| 名称 | 29.5 正多边形与圆 同步练习(含答案) 2024--2025学年冀教版九年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 414.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-04 00:00:00 | ||
图片预览

文档简介
29.5 正多边形与圆
一、选择题
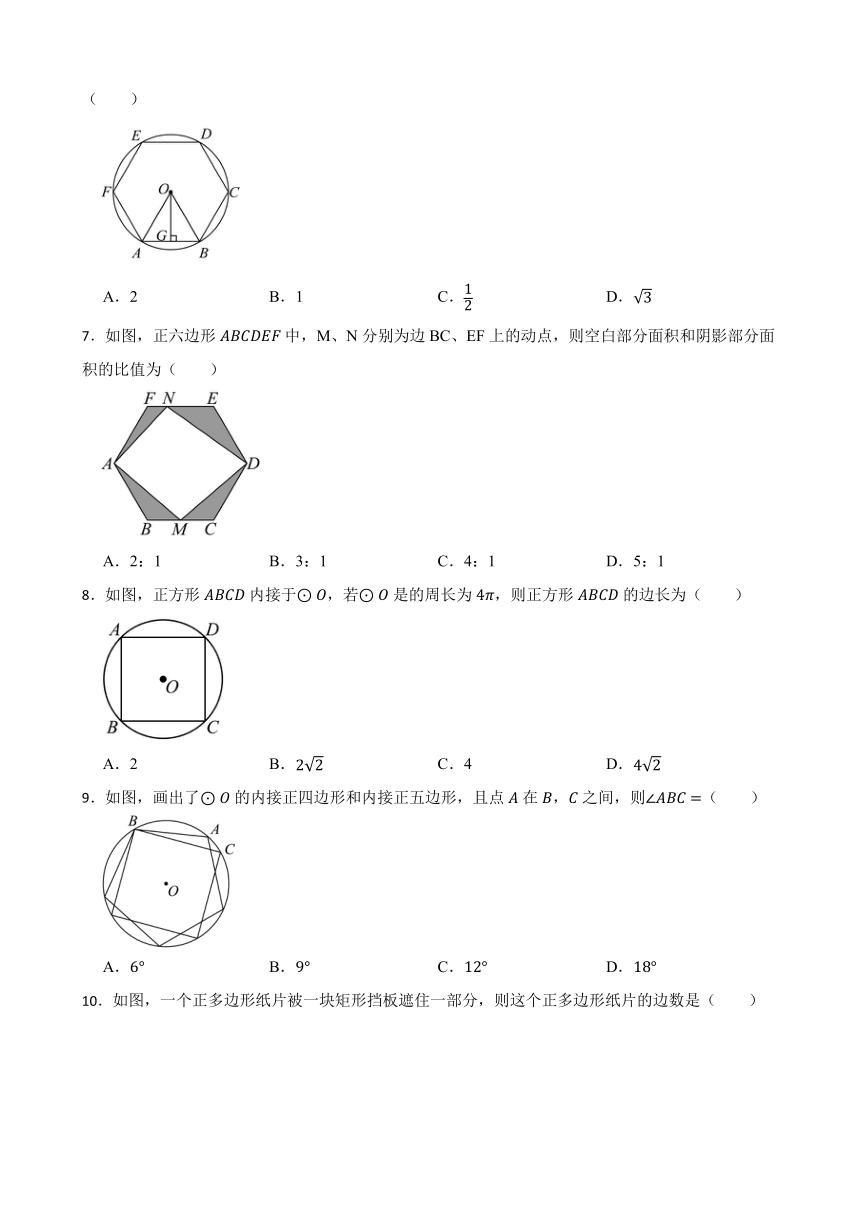
1.下列命题:①各角相等的多边形是正多边形;②任何正多边形都有一个外接圆和一个内切圆,并且这两个圆是同心圆;③正六边形的外接圆半径与边长相等;④在正多边形中,中心角与正多边形的每个外角相等.其中,真命题的个数是( )
A.4个 B.3个 C.2个 D.1个
2.如图,在正六边形ABCDEF中,△BCD的面积为4,则△BCF的面积为( )
A.16 B.12 C.8 D.6
3.风铃,又称铁马,古称“铎”,常见于中国传统建筑屋檐下(如图①),如图②是六角形风铃的平面示意图,其底部可抽象为正六边形,连接,则的度数为为( )
A. B. C. D.
4.周长相等的正方形与正六边形的面积分别为、,和的关系为( )
A. B.
C. D.
5.如图,正八边形内接于,连接,,则的度数为( )
A. B. C. D.
6.如图,的半径为2,正六边形内接于,则这个正六边形的边心距的长为( )
A.2 B.1 C. D.
7.如图,正六边形中,M、N分别为边BC、EF上的动点,则空白部分面积和阴影部分面积的比值为( )
A.2:1 B.3:1 C.4:1 D.5:1
8.如图,正方形内接于,若是的周长为,则正方形的边长为( )
A.2 B. C.4 D.
9.如图,画出了的内接正四边形和内接正五边形,且点在,之间,则( )
A. B. C. D.
10.如图,一个正多边形纸片被一块矩形挡板遮住一部分,则这个正多边形纸片的边数是( )
A.4 B.5 C.6 D.7
11.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )
A.cm B.9 cm C.cm D.cm
12.如图,是正六边形对角线上一点,延长,相交于点,若,则( )
A.10 B.12 C.14 D.16
13.公元3世纪,刘徽发现可以用圆内接正多边形的周长近似地表示圆的周长.如图所示,他首先在圆内画一个内接正六边形,再不断地增加正多边形的边数;当边数越多时,正多边形的周长就越接近于圆的周长.刘徽在《九章算术》中写道:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”我们称这种方法为刘徽割圆术,它开启了研究圆周率的新纪元.小牧通过圆内接正边形,使用刘徽割圆术,得到π的近似值为( )
A. B.
C. D.
二、填空题
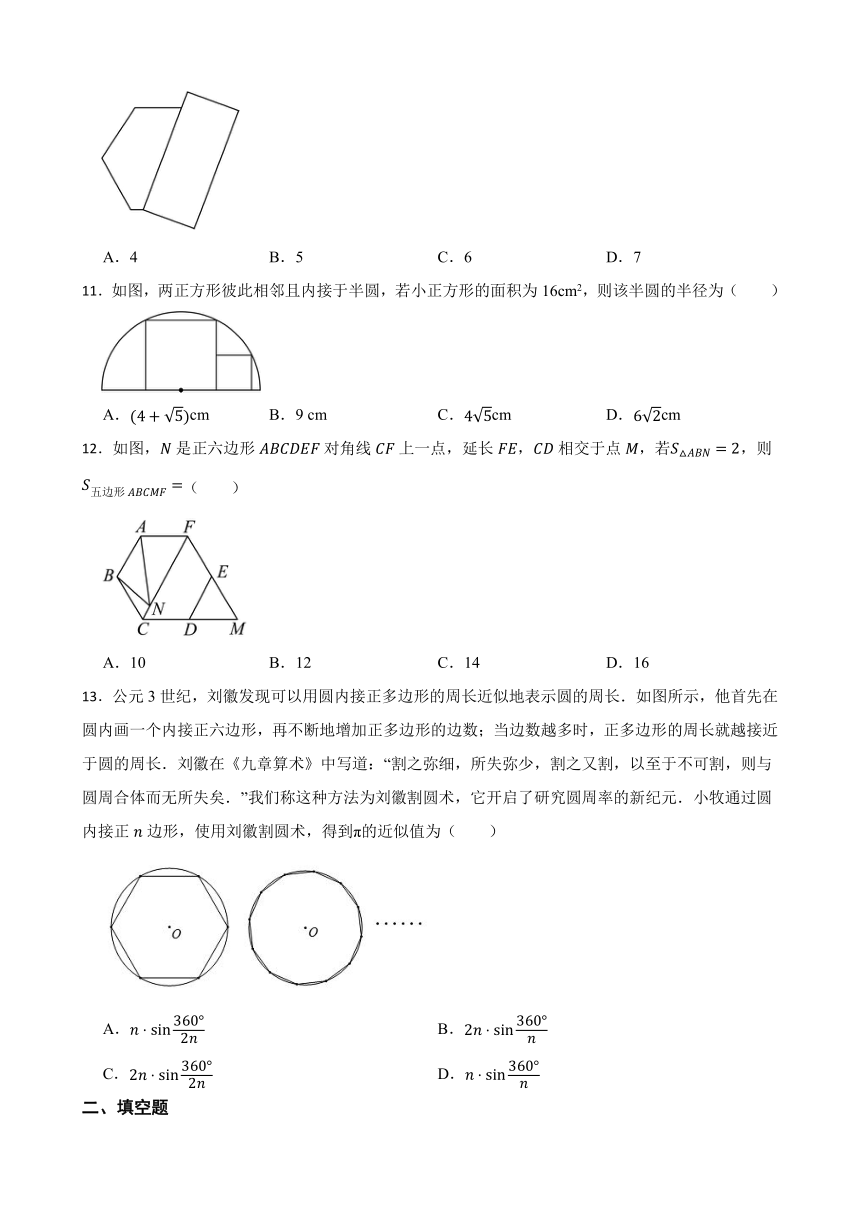
14.圆内接正三角形的中心角的度数为 .
15.如图,在拧开一个边长为的正六边形螺帽时,扳手张开的开口,则边长的长度是 .
16.如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是 个.
17.如图,正五边形内接于,连接,则 .
18.如图,、、、为一个正多边形的顶点,为正多边形的中心,若,则这个正多边形的边数为 .
三、解答题
19.如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.
20.如图,分别求出半径为R的圆内接正三角形圆内接正方形的周长和面积.
21.如图,正五边形的边长为6,以点B为圆心,线段为半径画圆.
(1)求的度数;
(2)求的长度.
22.如图1是学生常用的一种圆规,其手柄AB=8mm,两脚BC=BD=56mm,如图2所示.当时:
(1)求A离纸面CD的距离.
(2)用该圆规作如图3所示正六边形,求该正六边形的周长.(参考数据:sin37°≈0.60,cos37°≈0.80,sin74°≈0.96,cos74°≈0.28,结果精确到0.1)
答案
1.B
2.C
3.C
4.D
5.C
6.D
7.A
8.B
9.B
10.C
11.C
12.C
13.A
14.120°
15.
16.10
17.
18.九
19.解:∵正n边形边长为a,OM⊥AB,OA=OB,
∴AM= AB= a,
∵边心距为r,
∴正n边形的半径R= = = ;
∴周长P=na;
∴面积S=nS△OAB=n× a×r= nar
20.解:如图1,连接OB、OC,过O作OD⊥AB于D,
∵⊙O是正三角形ABC的外接圆,
∴∠AOB= =120°,
∵OA=OB,
∴∠AOD=∠BOD=60°,
在Rt△ADO中,AO=R,AD=R×sin60°= R,OD=Rcos60°= R,
∵OD⊥AB,
∴AB=2AD= R,
∴正△ABC的周长是3AB=3 R;面积是3× AB×OD=3× × R× R= R2;
如图2,连接OA、OB、OD,
∵⊙O是正方形ABCD的外接圆,
∴∠COD= =90°,
∵OD=OC=R,由勾股定理得;CD= = R,
∴正方形ABCD的周长为4× R=4 R,面积为 R× R=2R2.
21.(1)
(2)
22.(1)
(2)403.2mm
一、选择题
1.下列命题:①各角相等的多边形是正多边形;②任何正多边形都有一个外接圆和一个内切圆,并且这两个圆是同心圆;③正六边形的外接圆半径与边长相等;④在正多边形中,中心角与正多边形的每个外角相等.其中,真命题的个数是( )
A.4个 B.3个 C.2个 D.1个
2.如图,在正六边形ABCDEF中,△BCD的面积为4,则△BCF的面积为( )
A.16 B.12 C.8 D.6
3.风铃,又称铁马,古称“铎”,常见于中国传统建筑屋檐下(如图①),如图②是六角形风铃的平面示意图,其底部可抽象为正六边形,连接,则的度数为为( )
A. B. C. D.
4.周长相等的正方形与正六边形的面积分别为、,和的关系为( )
A. B.
C. D.
5.如图,正八边形内接于,连接,,则的度数为( )
A. B. C. D.
6.如图,的半径为2,正六边形内接于,则这个正六边形的边心距的长为( )
A.2 B.1 C. D.
7.如图,正六边形中,M、N分别为边BC、EF上的动点,则空白部分面积和阴影部分面积的比值为( )
A.2:1 B.3:1 C.4:1 D.5:1
8.如图,正方形内接于,若是的周长为,则正方形的边长为( )
A.2 B. C.4 D.
9.如图,画出了的内接正四边形和内接正五边形,且点在,之间,则( )
A. B. C. D.
10.如图,一个正多边形纸片被一块矩形挡板遮住一部分,则这个正多边形纸片的边数是( )
A.4 B.5 C.6 D.7
11.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )
A.cm B.9 cm C.cm D.cm
12.如图,是正六边形对角线上一点,延长,相交于点,若,则( )
A.10 B.12 C.14 D.16
13.公元3世纪,刘徽发现可以用圆内接正多边形的周长近似地表示圆的周长.如图所示,他首先在圆内画一个内接正六边形,再不断地增加正多边形的边数;当边数越多时,正多边形的周长就越接近于圆的周长.刘徽在《九章算术》中写道:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”我们称这种方法为刘徽割圆术,它开启了研究圆周率的新纪元.小牧通过圆内接正边形,使用刘徽割圆术,得到π的近似值为( )
A. B.
C. D.
二、填空题
14.圆内接正三角形的中心角的度数为 .
15.如图,在拧开一个边长为的正六边形螺帽时,扳手张开的开口,则边长的长度是 .
16.如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是 个.
17.如图,正五边形内接于,连接,则 .
18.如图,、、、为一个正多边形的顶点,为正多边形的中心,若,则这个正多边形的边数为 .
三、解答题
19.如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.
20.如图,分别求出半径为R的圆内接正三角形圆内接正方形的周长和面积.
21.如图,正五边形的边长为6,以点B为圆心,线段为半径画圆.
(1)求的度数;
(2)求的长度.
22.如图1是学生常用的一种圆规,其手柄AB=8mm,两脚BC=BD=56mm,如图2所示.当时:
(1)求A离纸面CD的距离.
(2)用该圆规作如图3所示正六边形,求该正六边形的周长.(参考数据:sin37°≈0.60,cos37°≈0.80,sin74°≈0.96,cos74°≈0.28,结果精确到0.1)
答案
1.B
2.C
3.C
4.D
5.C
6.D
7.A
8.B
9.B
10.C
11.C
12.C
13.A
14.120°
15.
16.10
17.
18.九
19.解:∵正n边形边长为a,OM⊥AB,OA=OB,
∴AM= AB= a,
∵边心距为r,
∴正n边形的半径R= = = ;
∴周长P=na;
∴面积S=nS△OAB=n× a×r= nar
20.解:如图1,连接OB、OC,过O作OD⊥AB于D,
∵⊙O是正三角形ABC的外接圆,
∴∠AOB= =120°,
∵OA=OB,
∴∠AOD=∠BOD=60°,
在Rt△ADO中,AO=R,AD=R×sin60°= R,OD=Rcos60°= R,
∵OD⊥AB,
∴AB=2AD= R,
∴正△ABC的周长是3AB=3 R;面积是3× AB×OD=3× × R× R= R2;
如图2,连接OA、OB、OD,
∵⊙O是正方形ABCD的外接圆,
∴∠COD= =90°,
∵OD=OC=R,由勾股定理得;CD= = R,
∴正方形ABCD的周长为4× R=4 R,面积为 R× R=2R2.
21.(1)
(2)
22.(1)
(2)403.2mm
