第14章 勾股定理 单元测试(含答案)2024-2025学年华东师大版数学八年级上册
文档属性
| 名称 | 第14章 勾股定理 单元测试(含答案)2024-2025学年华东师大版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 610.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-04 15:45:57 | ||
图片预览


文档简介
第14章 勾股定理单元测试
满分120分,测试时间90分钟
一、单选题(每小题4分,共40分)
1.在ABC中,,,,的对应边分别是,,,则下列式子成立的是( )
A. B. C. D.
2.下列数组中的数字,刚好是勾股数的一组是( )
A. B. C. D.
3.如图,所有阴影部分的四边形都是正方形,所有三角形都是直角三角形,已知正方形、、的面积依次为2、6、3,则正方形的面积为( )
A.6 B.8 C.11 D.12
4.某校“灯谜节”的奖品是一个底面为等边三角形的灯笼(如图),在灯笼的侧面上,从顶点A到顶点缠绕一圈彩带.已知此灯笼的高为50,底面边长为40,则这圈彩带的长度至少为( )
A.50 B.120 C.130 D.150
5.在中, ,,,则点C 到斜边的距离是( )
A. B. C.9 D.6
6.《算法统宗》记载古人丈量田地的诗:“昨日丈量地回,记得长步整三十.广斜相并五十步,不知几亩及分厘.”其大意是:昨天丈量了田地回到家,记得长方形田的长为30步,宽和对角线之和为50步.不知该田的面积有多少?设该长方形的对角线为步,则可列方程为( )
A. B. C. D.
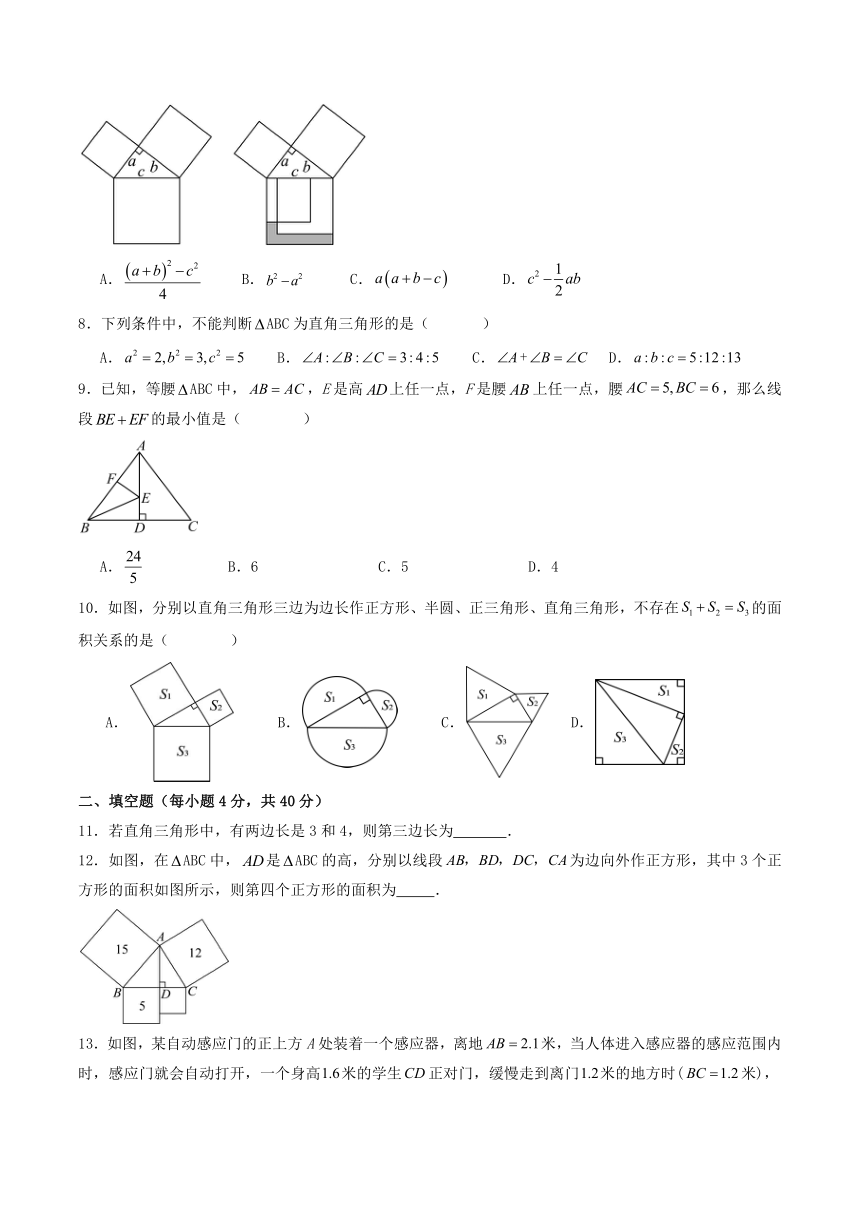
7.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.勾股定理描述:直角三角形两条直角边的平方和等于斜边的平方.如左图,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按右图的方式放置在最大正方形内.则图中阴影部分的面积为( )
A. B. C. D.
8.下列条件中,不能判断ABC为直角三角形的是( )
A. B. C. D.
9.已知,等腰ABC中,,E是高上任一点,F是腰上任一点,腰,那么线段的最小值是( )
A. B.6 C.5 D.4
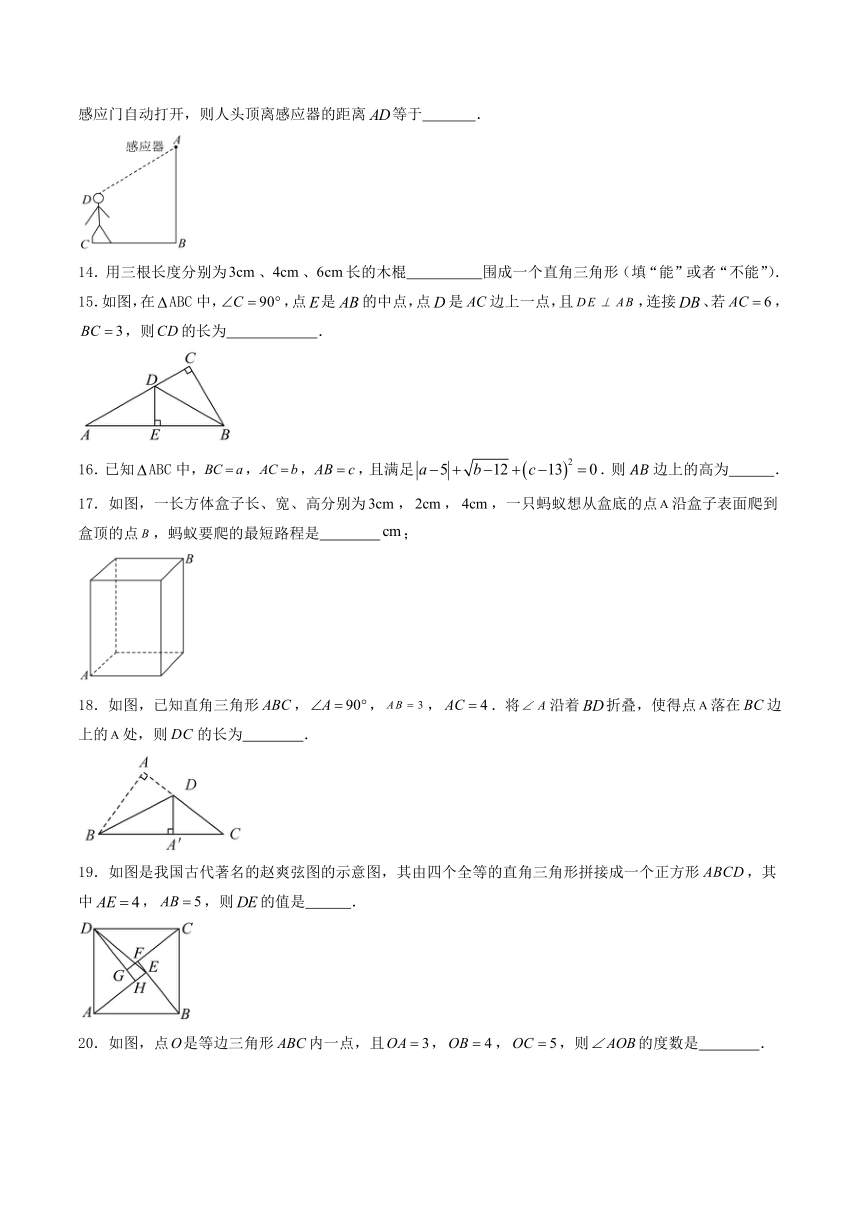
10.如图,分别以直角三角形三边为边长作正方形、半圆、正三角形、直角三角形,不存在的面积关系的是( )
A. B. C. D.
二、填空题(每小题4分,共40分)
11.若直角三角形中,有两边长是3和4,则第三边长为 .
12.如图,在ABC中,是ABC的高,分别以线段为边向外作正方形,其中3个正方形的面积如图所示,则第四个正方形的面积为 .
13.如图,某自动感应门的正上方A处装着一个感应器,离地米,当人体进入感应器的感应范围内时,感应门就会自动打开,一个身高米的学生正对门,缓慢走到离门米的地方时(米),感应门自动打开,则人头顶离感应器的距离等于 .
14.用三根长度分别为、、长的木棍 围成一个直角三角形(填“能”或者“不能”).
15.如图,在ABC中,,点是的中点,点是边上一点,且,连接、若,,则的长为 .
16.已知ABC中,,,,且满足.则边上的高为 .
17.如图,一长方体盒子长、宽、高分别为,,,一只蚂蚁想从盒底的点沿盒子表面爬到盒顶的点,蚂蚁要爬的最短路程是 ;
18.如图,已知直角三角形,,,.将沿着折叠,使得点落在边上的处,则的长为 .
19.如图是我国古代著名的赵爽弦图的示意图,其由四个全等的直角三角形拼接成一个正方形,其中,,则的值是 .
20.如图,点是等边三角形内一点,且,,,则的度数是 .
三、解答题(每小题8分,共40分)
21.如图,在直角三角形中,,于点,已知,.
(1)求斜边的长;
(2)求的长.
22.水利是农业的命脉,开远民间历来重视兴修水利,坝区明代即已筑堰修渠,开通东沟、西沟,引泸江、南洞水灌溉农田,经历代不断修拓完善,成为城郊灌溉干渠.这些沟渠凝聚了一代又一代开远人的智慧和心血,历经岁月磨砺、时光雕琢,成为最美的风景,在开远东沟的一侧有一个花卉基地C,基地到东沟原有两个取水点,其中,为方便花卉基地取水,决定在东沟新建一个取水点(、、在同一条直线上),并新修一条路,测得,,.
(1)求证:;
(2)求新路比原来的路少多少米.
23.2020年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知,,,,技术人员通过测量确定了.问这片绿地的面积是多少?
24.如图,在一条笔直的公路l旁边有A,B两个村庄,A村庄到公路l的距离,B村庄到公路l的距离,现要在之间建一个加油站E,使得A,B两村庄到加油站E的距离相等.
(1)若,试说明:;
(2)若C,D两点间的距离为,求C,E两点间的距离.
25.综合与实践
【背景介绍】勾股定理是几何学中的明珠,充满着魅力.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式,化简便得结论.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.
【方法运用】向常春在2010年构造发现了一个新的证法:把两个全等的直角和如图2放置,,显然.(对角线互相垂直的四边形的面积等于对角线乘积的一半)
(1)请用a,b,c分别表示出四边形,梯形的面积,再探究这三个图形面积之间的关系,证明勾股定理.
(2)【方法迁移】请利用“双求法”解决下面的问题:如图3,在中,,是边上的高,,求的长度;
(3)如图4,在ABC中,是边上的高,,求的长.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C C B B C B A D
11.5或 12.2 13.米 14.不能 15.
16. 17. 18. 19. 20.
21.(1)解:在直角三角形中,,,,
;
(2),
,
即,
.
22.(1)解:∵,,,
∴,,
∴,
∴为直角三角形,
.
(2)解:设,则,
∵,
∴,
∴, 即,解得:,
,
,,
即新路比原来的路少米.
23.解:如图,连接,
,,,
,
∵,,
,
∴是直角三角形,即,
,,
.
答:这片绿地的面积是.
24.解:(1)∵
∴
又∵
∴
在BDE在中:
∴
(2)解:设,则
∵,
∴
解得
∴
25.(1)解:,
,
,
,
,
化简得:;
(2)解:在中,,,
,
是边上的高,
,
;
(3)解:设,
在中,
,
,
,
在中,
,
,,
.
满分120分,测试时间90分钟
一、单选题(每小题4分,共40分)
1.在ABC中,,,,的对应边分别是,,,则下列式子成立的是( )
A. B. C. D.
2.下列数组中的数字,刚好是勾股数的一组是( )
A. B. C. D.
3.如图,所有阴影部分的四边形都是正方形,所有三角形都是直角三角形,已知正方形、、的面积依次为2、6、3,则正方形的面积为( )
A.6 B.8 C.11 D.12
4.某校“灯谜节”的奖品是一个底面为等边三角形的灯笼(如图),在灯笼的侧面上,从顶点A到顶点缠绕一圈彩带.已知此灯笼的高为50,底面边长为40,则这圈彩带的长度至少为( )
A.50 B.120 C.130 D.150
5.在中, ,,,则点C 到斜边的距离是( )
A. B. C.9 D.6
6.《算法统宗》记载古人丈量田地的诗:“昨日丈量地回,记得长步整三十.广斜相并五十步,不知几亩及分厘.”其大意是:昨天丈量了田地回到家,记得长方形田的长为30步,宽和对角线之和为50步.不知该田的面积有多少?设该长方形的对角线为步,则可列方程为( )
A. B. C. D.
7.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.勾股定理描述:直角三角形两条直角边的平方和等于斜边的平方.如左图,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按右图的方式放置在最大正方形内.则图中阴影部分的面积为( )
A. B. C. D.
8.下列条件中,不能判断ABC为直角三角形的是( )
A. B. C. D.
9.已知,等腰ABC中,,E是高上任一点,F是腰上任一点,腰,那么线段的最小值是( )
A. B.6 C.5 D.4
10.如图,分别以直角三角形三边为边长作正方形、半圆、正三角形、直角三角形,不存在的面积关系的是( )
A. B. C. D.
二、填空题(每小题4分,共40分)
11.若直角三角形中,有两边长是3和4,则第三边长为 .
12.如图,在ABC中,是ABC的高,分别以线段为边向外作正方形,其中3个正方形的面积如图所示,则第四个正方形的面积为 .
13.如图,某自动感应门的正上方A处装着一个感应器,离地米,当人体进入感应器的感应范围内时,感应门就会自动打开,一个身高米的学生正对门,缓慢走到离门米的地方时(米),感应门自动打开,则人头顶离感应器的距离等于 .
14.用三根长度分别为、、长的木棍 围成一个直角三角形(填“能”或者“不能”).
15.如图,在ABC中,,点是的中点,点是边上一点,且,连接、若,,则的长为 .
16.已知ABC中,,,,且满足.则边上的高为 .
17.如图,一长方体盒子长、宽、高分别为,,,一只蚂蚁想从盒底的点沿盒子表面爬到盒顶的点,蚂蚁要爬的最短路程是 ;
18.如图,已知直角三角形,,,.将沿着折叠,使得点落在边上的处,则的长为 .
19.如图是我国古代著名的赵爽弦图的示意图,其由四个全等的直角三角形拼接成一个正方形,其中,,则的值是 .
20.如图,点是等边三角形内一点,且,,,则的度数是 .
三、解答题(每小题8分,共40分)
21.如图,在直角三角形中,,于点,已知,.
(1)求斜边的长;
(2)求的长.
22.水利是农业的命脉,开远民间历来重视兴修水利,坝区明代即已筑堰修渠,开通东沟、西沟,引泸江、南洞水灌溉农田,经历代不断修拓完善,成为城郊灌溉干渠.这些沟渠凝聚了一代又一代开远人的智慧和心血,历经岁月磨砺、时光雕琢,成为最美的风景,在开远东沟的一侧有一个花卉基地C,基地到东沟原有两个取水点,其中,为方便花卉基地取水,决定在东沟新建一个取水点(、、在同一条直线上),并新修一条路,测得,,.
(1)求证:;
(2)求新路比原来的路少多少米.
23.2020年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知,,,,技术人员通过测量确定了.问这片绿地的面积是多少?
24.如图,在一条笔直的公路l旁边有A,B两个村庄,A村庄到公路l的距离,B村庄到公路l的距离,现要在之间建一个加油站E,使得A,B两村庄到加油站E的距离相等.
(1)若,试说明:;
(2)若C,D两点间的距离为,求C,E两点间的距离.
25.综合与实践
【背景介绍】勾股定理是几何学中的明珠,充满着魅力.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式,化简便得结论.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.
【方法运用】向常春在2010年构造发现了一个新的证法:把两个全等的直角和如图2放置,,显然.(对角线互相垂直的四边形的面积等于对角线乘积的一半)
(1)请用a,b,c分别表示出四边形,梯形的面积,再探究这三个图形面积之间的关系,证明勾股定理.
(2)【方法迁移】请利用“双求法”解决下面的问题:如图3,在中,,是边上的高,,求的长度;
(3)如图4,在ABC中,是边上的高,,求的长.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C C B B C B A D
11.5或 12.2 13.米 14.不能 15.
16. 17. 18. 19. 20.
21.(1)解:在直角三角形中,,,,
;
(2),
,
即,
.
22.(1)解:∵,,,
∴,,
∴,
∴为直角三角形,
.
(2)解:设,则,
∵,
∴,
∴, 即,解得:,
,
,,
即新路比原来的路少米.
23.解:如图,连接,
,,,
,
∵,,
,
∴是直角三角形,即,
,,
.
答:这片绿地的面积是.
24.解:(1)∵
∴
又∵
∴
在BDE在中:
∴
(2)解:设,则
∵,
∴
解得
∴
25.(1)解:,
,
,
,
,
化简得:;
(2)解:在中,,,
,
是边上的高,
,
;
(3)解:设,
在中,
,
,
,
在中,
,
,,
.
