第15章 数据的收集与表示 单元测试(含答案)2024-2025学年华东师大版数学八年级上册
文档属性
| 名称 | 第15章 数据的收集与表示 单元测试(含答案)2024-2025学年华东师大版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 574.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-04 15:46:49 | ||
图片预览



文档简介
第15章 数据的收集与表示单元测试
满分120分,测试时间90分钟
一、单选题(每小题4分,共40分)
1.小明掷骰子,要保证掷出的点数至少有两次相同,他至少应掷( )次.
A.6 B.7 C.8 D.9
2.如图是我市某景点6月份内日每天的最高温度折线统计图,由图信息可知该景点这10天中,气温出现的频率是( )
A.3 B.0.5 C.0.4 D.0.3
3.要调查某校七年级学生周一到周五平均每天的睡眠时间,选取调查对象最合适的是( )
A.选取该校七年级一个班级的学生 B.选取60名该校的七年级女生
C.选取60名该校的七年级男生 D.随机选取60名该校的七年级学生
4.随着时代进步,现代化信息技术与传统教学方式深度融合.学校为了解学生对现代化教学方式的喜爱程度,随机抽取200名学生根据以下四个步骤完成统计调查:①从扇形统计图中分析出学生对现代化教学方式的喜爱程度;②随机抽取200名学生,发放调查问卷,利用问卷收集数据;③根据频数分布表绘制扇形统计图;④整理收集的数据并绘制频数分布表.这四个步骤合理的排序为( )
A. B. C. D.
5.已知一个含40个数据的样本,把它分成六组,第一组到第五组的频数分别为10,5,7,6,4,则第六组的频数为 .
6.小明家要买一台电脑,下面是甲、乙、丙三种电脑近几年来的销售情况,如果小明想买一台比较流行的电脑,他应买( )
甲 乙 丙
2018年 600 590 650
2019年 610 650 670
2020年 590 700 660
A.甲 B.乙 C.丙 D.乙或丙
7.如图是某家新华书店以下5类书籍:小说、儿童读物、专业书、工具书、摄影绘画集,某月的销量情况的扇形统计图,由图可知,下列说法错误的是( )
A.扇形统计图能反映出该书店本月小说类比工具书类销售出的书籍多
B.小说类和儿童读物类书籍本月的销量占比之和为总销量的一半
C.摄影绘画集类书籍本月的销量所对应的扇形圆心角的度数为
D.专业书类和摄影绘画集类书籍本月的销量占比相同
8.交通安全知识竞赛成绩统计如下表:
分数段 61分~70分 71分~80分 81分~90分 91分~100分
频数 1 19 22 18
成绩在91分~100分的为优秀者,则优秀者的频率是( )
A. B. C. D.
9.在一个不透明的布袋中装有红色,绿色玻璃球共20个.这些玻璃球除颜色外其他完全相同,每次把布袋中的玻璃球摇匀后随机摸出一个,记下颜色后放回,摇匀后再从中随机摸出一个.小明通过多次摸球试验后发现,其中摸到红色玻璃球的频率稳定在左右,则口袋中红色玻璃球可能有( )
A.17个 B.14个 C.5个 D.3个
10.在某市青少年航空航天模型锦标赛中,各年龄组的参赛人数情况如表所示:
年龄组 岁 岁 岁 岁
参赛人数 5 19 12 14
若小明所在年龄组的参赛人数的频率为,则小明所在的年龄组是( )
A.13岁 B.14岁 C.15岁 D.16岁
二、填空题(每小题4分,共40分)
11.将一批数据分成4组,并列出频率分布表,其中第一组的频率是0.23,第二组与第四组的频率之和是0.52,那么第三组的频率是 .
12.在条形统计图中,若各个小长方形的面积比为,则用扇形统计图表示时,各扇形的圆心角的度数分别为 .
13.要了解某校七年级1200名学生的体重情况,请你运用所学的统计知识,将解决上述问题要经历的几个重要步骤进行排序:①收集数据;②设计调查问卷;③用样本估计总体;④整理数据;⑤分析数据.正确的排序为 .(填序号)
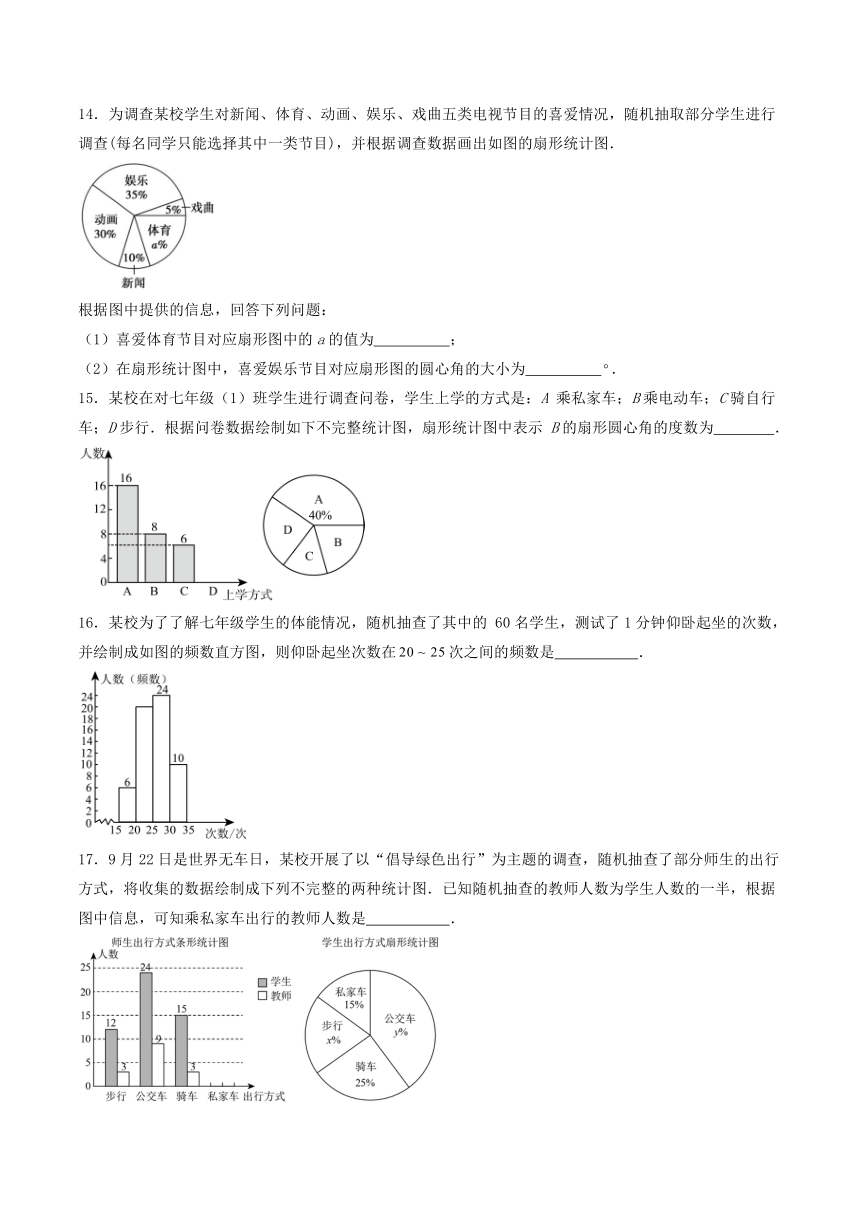
14.为调查某校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查(每名同学只能选择其中一类节目),并根据调查数据画出如图的扇形统计图.
根据图中提供的信息,回答下列问题:
(1)喜爱体育节目对应扇形图中的a的值为 ;
(2)在扇形统计图中,喜爱娱乐节目对应扇形图的圆心角的大小为 .
15.某校在对七年级(1)班学生进行调查问卷,学生上学的方式是:A 乘私家车;B乘电动车;C骑自行车;D步行.根据问卷数据绘制如下不完整统计图,扇形统计图中表示 B的扇形圆心角的度数为 .
16.某校为了了解七年级学生的体能情况,随机抽查了其中的 60名学生,测试了1分钟仰卧起坐的次数,并绘制成如图的频数直方图,则仰卧起坐次数在次之间的频数是 .
17.9月22日是世界无车日,某校开展了以“倡导绿色出行”为主题的调查,随机抽查了部分师生的出行方式,将收集的数据绘制成下列不完整的两种统计图.已知随机抽查的教师人数为学生人数的一半,根据图中信息,可知乘私家车出行的教师人数是 .
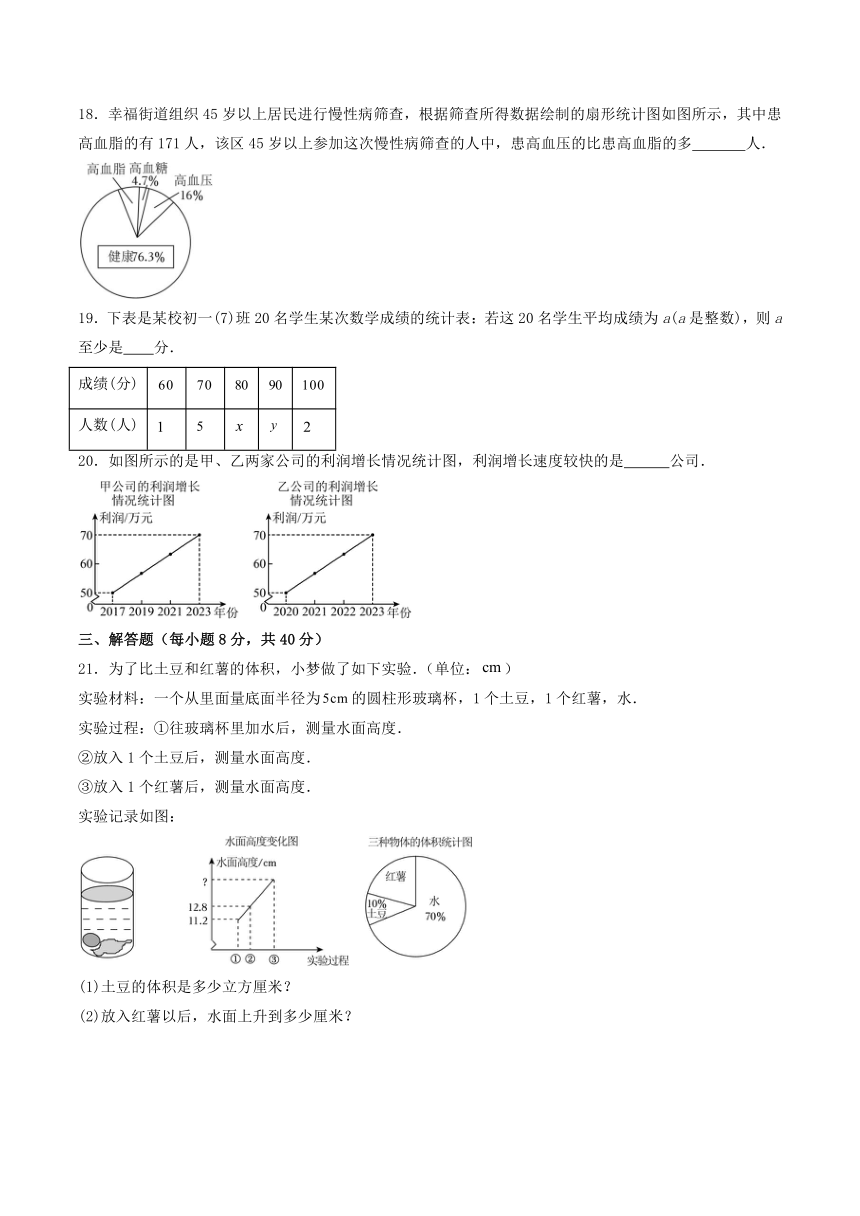
18.幸福街道组织45岁以上居民进行慢性病筛查,根据筛查所得数据绘制的扇形统计图如图所示,其中患高血脂的有171人,该区45岁以上参加这次慢性病筛查的人中,患高血压的比患高血脂的多 人.
19.下表是某校初一(7)班20名学生某次数学成绩的统计表:若这20名学生平均成绩为a(a是整数),则a至少是 分.
成绩(分)
人数(人)
20.如图所示的是甲、乙两家公司的利润增长情况统计图,利润增长速度较快的是 公司.
三、解答题(每小题8分,共40分)
21.为了比土豆和红薯的体积,小梦做了如下实验.(单位:)
实验材料:一个从里面量底面半径为的圆柱形玻璃杯,1个土豆,1个红薯,水.
实验过程:①往玻璃杯里加水后,测量水面高度.
②放入1个土豆后,测量水面高度.
③放入1个红薯后,测量水面高度.
实验记录如图:
(1)土豆的体积是多少立方厘米?
(2)放入红薯以后,水面上升到多少厘米?
22.下面是一幢居民楼内的家庭人口情况统计表.根据下表制作扇形统计图,表示家庭人口数分别是2,3,4,5的户数占这一幢居民楼总户数的百分比.
家庭人口数 2 3 4 5
户数 8 22 6 4
(1)分别计算家庭人口数是2,3,4,5的户数占总户数的百分比;
(2)分别计算家庭人口数是2,3,4,5的户数所对应的扇形的圆心角的度数;
(3)画出扇形统计图.
23.以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬物发展.进而对相关人才的需求更加旺盛.某大型科技公司上半年新招聘了软件、硬件、总线、测试四类专业的毕业生若干,现从中随机调查了名新聘毕业生的专业情况,并将调查结果绘制成了统计图(以下给出的是两幅不完整的统计图).
请根据统计图提供的信息,解答下列问题.
(1) 名, ;
(2)被调查的对象中是“硬件”专业的人数为 ,并补全条形统计图;
(3)在扇形统计图中,“软件”所对应的扇形的圆心角是 度;
(4)如果该公司新招聘的毕业生总数是600名,请你估计“总线”专业的毕业生有 名.
24.某小学为了解本校六年级学生的语文和数学期末成绩(满分均为100分),从该校600名六年级学生中随机抽取了50名学生的成绩,并绘制成如下统计图表.
50名学生的语文和数学成绩统计表
成绩 语文(人) 数学(人)
1 a
16 17
m b
请你根据以上信息,回答下列问题:
(1)填空: , , ;
(2)这50组抽样数据中,两个学科成绩都低于60分的学生有 人;
(3)在小学高年级阶段,“双优(两个学科成绩都大于或等于80分的学生人数)”“双及(两个学科成绩都大于或等于60分的学生人数)”是评价综合成绩是一项重要的指标.请对照统计图,通过计算估计本次期末成绩中,该校六年级学生语文和数学“双优”“双及”的人数分别是多少人?
25.垃圾分类,事关人居环境改善,是当前世界各国共同关注的迫切问题.某校开展“垃圾分类”宣传活动,一个社团在开展“垃圾分类”宣传活动前、后分别对全校学生开展了抽样调查,将统计数据整理如下:开展“垃圾分类”宣传活动之前各类别统计表
类别 人数 A.每次分类 B.经常分类 C.偶尔分类 D.都不分类
A 7
B 25
C 52
D 16
合计 100
开展“垃圾分类”宣传活动之后各类别统计图(调查人数200人)
(1)开展“垃圾分类”宣传活动前,抽取的学生中哪一类别的人数最多?占抽取人数的百分之几?
(2)若全校有2000名学生,请估计开展“垃圾分类”宣传活动前“D.都不分类”的总人数;
(3)李琳认为,开展“垃圾分类”宣传活动后,“D.都不分类”的人数为人,与活动前的人数一样,所以“垃圾分类”宣传活动开展不到位,她分析数据的方法是否合理?请结合统计图表,对学校开展“垃圾分类”宣传活动的效果谈谈你的看法.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D D 8 B C B D B
11.0.25 12.,,, 13.②①④⑤③ 14. 20 126 15.
16.20 17.15 18.741 19.79 20.乙
21.(1)解:
(立方厘米),
答:土豆的体积是立方厘米.
(2)解:由扇形图知:红薯占总体积的,
红薯的体积是土豆体积的2倍,
玻璃杯里放入红薯后,水面上升的高度是玻璃杯里放入土豆后水面上升高度的2倍,
玻璃杯里放入红薯后,水面上升的高度是(厘米),
放入红薯以后,水面上升到厘米.
22.(1)解:根据题意,得这幢居民楼内的总户数为,则家庭人口数是的户数占总户数的百分比为,
家庭人口数是的户数占总户数的百分比为,
家庭人口数是的户数占总户数的百分比为,
家庭人口数是的户数占总户数的百分比为.
(2)家庭人口数是的户数所对应的扇形的圆心角的度数为,
家庭人口数是的户数所对应的扇形的圆心角的度数为,
家庭人口数是的户数所对应的扇形的圆心角的度数为,
家庭人口数是的户数所对应的扇形的圆心角的度数为.
(3)所画的扇形统计图如答图.
23.(1)解:由条形统计图与扇形统计图中对应信息可知,,,
故答案为:50,10;
(2)解:由(1)可知硬件专业的毕业生有:(人,
补全的条形统计图如图所示:
故答案为:20,补全条形统计图见解析;
(3)解:在扇形统计图中,“软件”所对应的扇形的圆心角是,
故答案为:72;
(4)解:(名,
即“总线”专业的毕业生有180名,
故答案为:180.
24.(1)解:由统计图可得:语文成绩在之间的有33人,
∴;
数学成绩在之间的有6人,
∴;
数学成绩在之间的有27人,
∴;
(2)解:根据50名学生的语文和数学成绩统计表可得:两个学科成绩都低于60分的学生有1人;
(3)解:“双优”:(人).
“双及”:(人).
25.解:(1)根据题意,得“偶尔分类”的人数最多,占比为:=;
(2)根据题意,得:=320(人);
(3)不合理;活动前,“都不分类”占比为:=;活动后,占比为:=,占比明显降低了,活动前,“偶尔分类”占比为:=;活动后,占比为:,占比明显降低了,
活动前,“每次分类”占比为:=;活动后,占比为:,占比明显提高了,
活动前,“经常分类”占比为:=;活动后,占比为:,占比明显提高了,可见学生的垃圾分类意识显著改变,宣传效果非常明显.
满分120分,测试时间90分钟
一、单选题(每小题4分,共40分)
1.小明掷骰子,要保证掷出的点数至少有两次相同,他至少应掷( )次.
A.6 B.7 C.8 D.9
2.如图是我市某景点6月份内日每天的最高温度折线统计图,由图信息可知该景点这10天中,气温出现的频率是( )
A.3 B.0.5 C.0.4 D.0.3
3.要调查某校七年级学生周一到周五平均每天的睡眠时间,选取调查对象最合适的是( )
A.选取该校七年级一个班级的学生 B.选取60名该校的七年级女生
C.选取60名该校的七年级男生 D.随机选取60名该校的七年级学生
4.随着时代进步,现代化信息技术与传统教学方式深度融合.学校为了解学生对现代化教学方式的喜爱程度,随机抽取200名学生根据以下四个步骤完成统计调查:①从扇形统计图中分析出学生对现代化教学方式的喜爱程度;②随机抽取200名学生,发放调查问卷,利用问卷收集数据;③根据频数分布表绘制扇形统计图;④整理收集的数据并绘制频数分布表.这四个步骤合理的排序为( )
A. B. C. D.
5.已知一个含40个数据的样本,把它分成六组,第一组到第五组的频数分别为10,5,7,6,4,则第六组的频数为 .
6.小明家要买一台电脑,下面是甲、乙、丙三种电脑近几年来的销售情况,如果小明想买一台比较流行的电脑,他应买( )
甲 乙 丙
2018年 600 590 650
2019年 610 650 670
2020年 590 700 660
A.甲 B.乙 C.丙 D.乙或丙
7.如图是某家新华书店以下5类书籍:小说、儿童读物、专业书、工具书、摄影绘画集,某月的销量情况的扇形统计图,由图可知,下列说法错误的是( )
A.扇形统计图能反映出该书店本月小说类比工具书类销售出的书籍多
B.小说类和儿童读物类书籍本月的销量占比之和为总销量的一半
C.摄影绘画集类书籍本月的销量所对应的扇形圆心角的度数为
D.专业书类和摄影绘画集类书籍本月的销量占比相同
8.交通安全知识竞赛成绩统计如下表:
分数段 61分~70分 71分~80分 81分~90分 91分~100分
频数 1 19 22 18
成绩在91分~100分的为优秀者,则优秀者的频率是( )
A. B. C. D.
9.在一个不透明的布袋中装有红色,绿色玻璃球共20个.这些玻璃球除颜色外其他完全相同,每次把布袋中的玻璃球摇匀后随机摸出一个,记下颜色后放回,摇匀后再从中随机摸出一个.小明通过多次摸球试验后发现,其中摸到红色玻璃球的频率稳定在左右,则口袋中红色玻璃球可能有( )
A.17个 B.14个 C.5个 D.3个
10.在某市青少年航空航天模型锦标赛中,各年龄组的参赛人数情况如表所示:
年龄组 岁 岁 岁 岁
参赛人数 5 19 12 14
若小明所在年龄组的参赛人数的频率为,则小明所在的年龄组是( )
A.13岁 B.14岁 C.15岁 D.16岁
二、填空题(每小题4分,共40分)
11.将一批数据分成4组,并列出频率分布表,其中第一组的频率是0.23,第二组与第四组的频率之和是0.52,那么第三组的频率是 .
12.在条形统计图中,若各个小长方形的面积比为,则用扇形统计图表示时,各扇形的圆心角的度数分别为 .
13.要了解某校七年级1200名学生的体重情况,请你运用所学的统计知识,将解决上述问题要经历的几个重要步骤进行排序:①收集数据;②设计调查问卷;③用样本估计总体;④整理数据;⑤分析数据.正确的排序为 .(填序号)
14.为调查某校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查(每名同学只能选择其中一类节目),并根据调查数据画出如图的扇形统计图.
根据图中提供的信息,回答下列问题:
(1)喜爱体育节目对应扇形图中的a的值为 ;
(2)在扇形统计图中,喜爱娱乐节目对应扇形图的圆心角的大小为 .
15.某校在对七年级(1)班学生进行调查问卷,学生上学的方式是:A 乘私家车;B乘电动车;C骑自行车;D步行.根据问卷数据绘制如下不完整统计图,扇形统计图中表示 B的扇形圆心角的度数为 .
16.某校为了了解七年级学生的体能情况,随机抽查了其中的 60名学生,测试了1分钟仰卧起坐的次数,并绘制成如图的频数直方图,则仰卧起坐次数在次之间的频数是 .
17.9月22日是世界无车日,某校开展了以“倡导绿色出行”为主题的调查,随机抽查了部分师生的出行方式,将收集的数据绘制成下列不完整的两种统计图.已知随机抽查的教师人数为学生人数的一半,根据图中信息,可知乘私家车出行的教师人数是 .
18.幸福街道组织45岁以上居民进行慢性病筛查,根据筛查所得数据绘制的扇形统计图如图所示,其中患高血脂的有171人,该区45岁以上参加这次慢性病筛查的人中,患高血压的比患高血脂的多 人.
19.下表是某校初一(7)班20名学生某次数学成绩的统计表:若这20名学生平均成绩为a(a是整数),则a至少是 分.
成绩(分)
人数(人)
20.如图所示的是甲、乙两家公司的利润增长情况统计图,利润增长速度较快的是 公司.
三、解答题(每小题8分,共40分)
21.为了比土豆和红薯的体积,小梦做了如下实验.(单位:)
实验材料:一个从里面量底面半径为的圆柱形玻璃杯,1个土豆,1个红薯,水.
实验过程:①往玻璃杯里加水后,测量水面高度.
②放入1个土豆后,测量水面高度.
③放入1个红薯后,测量水面高度.
实验记录如图:
(1)土豆的体积是多少立方厘米?
(2)放入红薯以后,水面上升到多少厘米?
22.下面是一幢居民楼内的家庭人口情况统计表.根据下表制作扇形统计图,表示家庭人口数分别是2,3,4,5的户数占这一幢居民楼总户数的百分比.
家庭人口数 2 3 4 5
户数 8 22 6 4
(1)分别计算家庭人口数是2,3,4,5的户数占总户数的百分比;
(2)分别计算家庭人口数是2,3,4,5的户数所对应的扇形的圆心角的度数;
(3)画出扇形统计图.
23.以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬物发展.进而对相关人才的需求更加旺盛.某大型科技公司上半年新招聘了软件、硬件、总线、测试四类专业的毕业生若干,现从中随机调查了名新聘毕业生的专业情况,并将调查结果绘制成了统计图(以下给出的是两幅不完整的统计图).
请根据统计图提供的信息,解答下列问题.
(1) 名, ;
(2)被调查的对象中是“硬件”专业的人数为 ,并补全条形统计图;
(3)在扇形统计图中,“软件”所对应的扇形的圆心角是 度;
(4)如果该公司新招聘的毕业生总数是600名,请你估计“总线”专业的毕业生有 名.
24.某小学为了解本校六年级学生的语文和数学期末成绩(满分均为100分),从该校600名六年级学生中随机抽取了50名学生的成绩,并绘制成如下统计图表.
50名学生的语文和数学成绩统计表
成绩 语文(人) 数学(人)
1 a
16 17
m b
请你根据以上信息,回答下列问题:
(1)填空: , , ;
(2)这50组抽样数据中,两个学科成绩都低于60分的学生有 人;
(3)在小学高年级阶段,“双优(两个学科成绩都大于或等于80分的学生人数)”“双及(两个学科成绩都大于或等于60分的学生人数)”是评价综合成绩是一项重要的指标.请对照统计图,通过计算估计本次期末成绩中,该校六年级学生语文和数学“双优”“双及”的人数分别是多少人?
25.垃圾分类,事关人居环境改善,是当前世界各国共同关注的迫切问题.某校开展“垃圾分类”宣传活动,一个社团在开展“垃圾分类”宣传活动前、后分别对全校学生开展了抽样调查,将统计数据整理如下:开展“垃圾分类”宣传活动之前各类别统计表
类别 人数 A.每次分类 B.经常分类 C.偶尔分类 D.都不分类
A 7
B 25
C 52
D 16
合计 100
开展“垃圾分类”宣传活动之后各类别统计图(调查人数200人)
(1)开展“垃圾分类”宣传活动前,抽取的学生中哪一类别的人数最多?占抽取人数的百分之几?
(2)若全校有2000名学生,请估计开展“垃圾分类”宣传活动前“D.都不分类”的总人数;
(3)李琳认为,开展“垃圾分类”宣传活动后,“D.都不分类”的人数为人,与活动前的人数一样,所以“垃圾分类”宣传活动开展不到位,她分析数据的方法是否合理?请结合统计图表,对学校开展“垃圾分类”宣传活动的效果谈谈你的看法.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D D 8 B C B D B
11.0.25 12.,,, 13.②①④⑤③ 14. 20 126 15.
16.20 17.15 18.741 19.79 20.乙
21.(1)解:
(立方厘米),
答:土豆的体积是立方厘米.
(2)解:由扇形图知:红薯占总体积的,
红薯的体积是土豆体积的2倍,
玻璃杯里放入红薯后,水面上升的高度是玻璃杯里放入土豆后水面上升高度的2倍,
玻璃杯里放入红薯后,水面上升的高度是(厘米),
放入红薯以后,水面上升到厘米.
22.(1)解:根据题意,得这幢居民楼内的总户数为,则家庭人口数是的户数占总户数的百分比为,
家庭人口数是的户数占总户数的百分比为,
家庭人口数是的户数占总户数的百分比为,
家庭人口数是的户数占总户数的百分比为.
(2)家庭人口数是的户数所对应的扇形的圆心角的度数为,
家庭人口数是的户数所对应的扇形的圆心角的度数为,
家庭人口数是的户数所对应的扇形的圆心角的度数为,
家庭人口数是的户数所对应的扇形的圆心角的度数为.
(3)所画的扇形统计图如答图.
23.(1)解:由条形统计图与扇形统计图中对应信息可知,,,
故答案为:50,10;
(2)解:由(1)可知硬件专业的毕业生有:(人,
补全的条形统计图如图所示:
故答案为:20,补全条形统计图见解析;
(3)解:在扇形统计图中,“软件”所对应的扇形的圆心角是,
故答案为:72;
(4)解:(名,
即“总线”专业的毕业生有180名,
故答案为:180.
24.(1)解:由统计图可得:语文成绩在之间的有33人,
∴;
数学成绩在之间的有6人,
∴;
数学成绩在之间的有27人,
∴;
(2)解:根据50名学生的语文和数学成绩统计表可得:两个学科成绩都低于60分的学生有1人;
(3)解:“双优”:(人).
“双及”:(人).
25.解:(1)根据题意,得“偶尔分类”的人数最多,占比为:=;
(2)根据题意,得:=320(人);
(3)不合理;活动前,“都不分类”占比为:=;活动后,占比为:=,占比明显降低了,活动前,“偶尔分类”占比为:=;活动后,占比为:,占比明显降低了,
活动前,“每次分类”占比为:=;活动后,占比为:,占比明显提高了,
活动前,“经常分类”占比为:=;活动后,占比为:,占比明显提高了,可见学生的垃圾分类意识显著改变,宣传效果非常明显.
