第26章 反比例函数 能力提升测试题(含详解)2024-2025学年人教版数学九年级下册
文档属性
| 名称 | 第26章 反比例函数 能力提升测试题(含详解)2024-2025学年人教版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 241.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-04 00:00:00 | ||
图片预览


文档简介
第26章 反比例函数能力提升测试题
考试范围:第26章 反比例函数;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.若y=(a+1)x|a|﹣2是反比例函数,则a的取值为( )
A.1 B.﹣1 C.±1 D.任意实数
2.若点P1(x1,y1),P2(x2,y2)在反比例函数y(k>0)的图象上,且x1=﹣x2,则( )
A.y1<y2 B.y1=y2 C.y1>y2 D.y1=﹣y2
3.已知A(﹣1,y1),B(3,y2)两点在双曲线y上,且y1>y2,则m的取值范围是( )
A.m<0 B.m>0 C.m D.m
4.如图,正比例函数y1与反比例函数y2相交于点E(﹣1,2),若y1>y2>0,则x的取值范围在数轴上表示正确的是( )
A. B.
C. D.
5.某种气球内充满了一定质量的气体,当温度不变时,气球内的气体的气压P(kPa)是气球体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将爆炸,为了安全,气球的体积应该( )
A.不大于m3 B.小于m3
C.不小于m3 D.小于m3
6.如图,点B在y轴的正半轴上,点C在反比例函数y(x<0)的图象上,菱形OABC的面积为8,则k的值为( )
A.﹣4 B.4 C.﹣2 D.2
7.在平面直角坐标系中,分别过点A(m,0),B(m+2,0)作x轴的垂线l1和l2,探究直线l1,直线l2与双曲线y的关系,下列结论中错误的是( )
A.两直线中总有一条与双曲线相交
B.当m=1时,两直线与双曲线的交点到原点的距离相等
C.当﹣2<m<0时,两直线与双曲线的交点在y轴两侧
D.当两直线与双曲线都有交点时,这两交点的最短距离是2
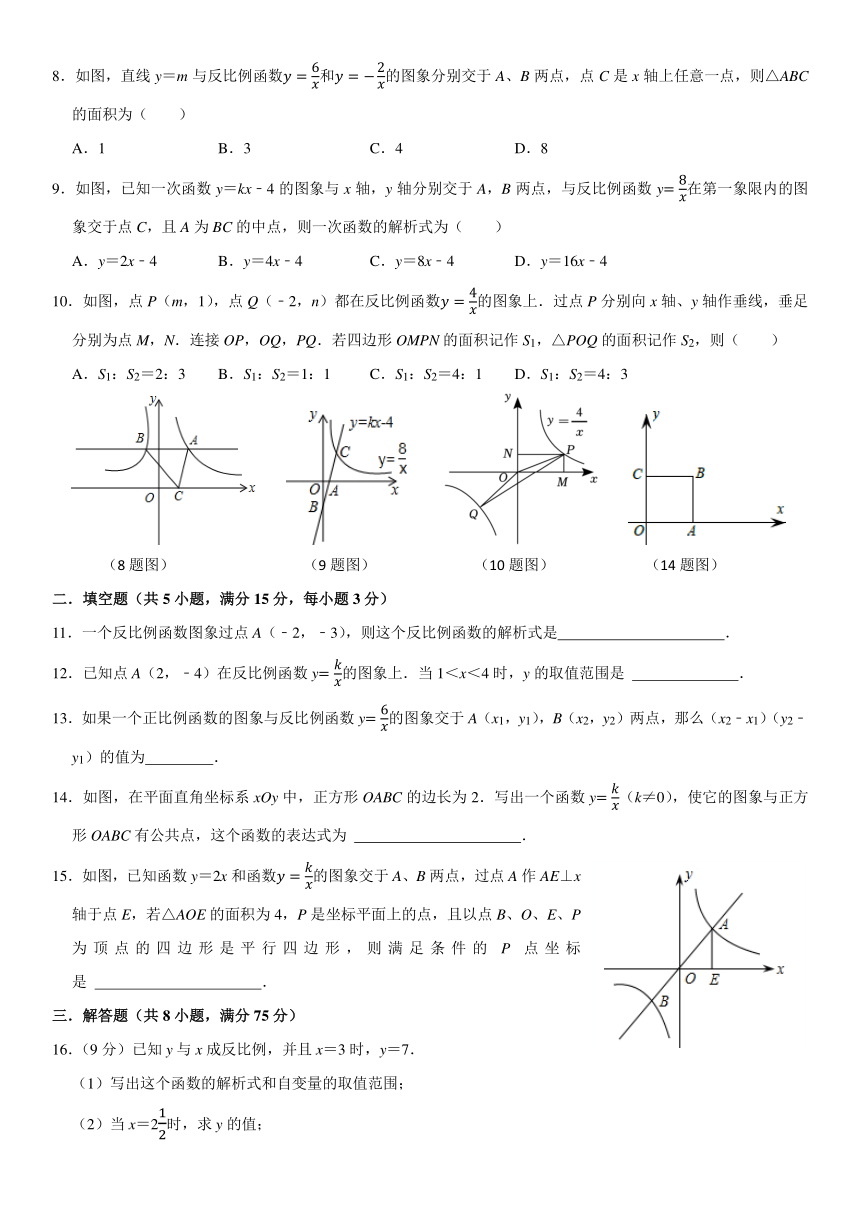
8.如图,直线y=m与反比例函数和的图象分别交于A、B两点,点C是x轴上任意一点,则△ABC的面积为( )
A.1 B.3 C.4 D.8
9.如图,已知一次函数y=kx﹣4的图象与x轴,y轴分别交于A,B两点,与反比例函数y在第一象限内的图象交于点C,且A为BC的中点,则一次函数的解析式为( )
A.y=2x﹣4 B.y=4x﹣4 C.y=8x﹣4 D.y=16x﹣4
10.如图,点P(m,1),点Q(﹣2,n)都在反比例函数的图象上.过点P分别向x轴、y轴作垂线,垂足分别为点M,N.连接OP,OQ,PQ.若四边形OMPN的面积记作S1,△POQ的面积记作S2,则( )
A.S1:S2=2:3 B.S1:S2=1:1 C.S1:S2=4:1 D.S1:S2=4:3
(8题图) (9题图) (10题图) (14题图)
二.填空题(共5小题,满分15分,每小题3分)
11.一个反比例函数图象过点A(﹣2,﹣3),则这个反比例函数的解析式是 .
12.已知点A(2,﹣4)在反比例函数y的图象上.当1<x<4时,y的取值范围是 .
13.如果一个正比例函数的图象与反比例函数y的图象交于A(x1,y1),B(x2,y2)两点,那么(x2﹣x1)(y2﹣y1)的值为 .
14.如图,在平面直角坐标系xOy中,正方形OABC的边长为2.写出一个函数y(k≠0),使它的图象与正方形OABC有公共点,这个函数的表达式为 .
15.如图,已知函数y=2x和函数的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,则满足条件的P点坐标是 .
三.解答题(共8小题,满分75分)
16.(9分)已知y与x成反比例,并且x=3时,y=7.
(1)写出这个函数的解析式和自变量的取值范围;
(2)当x=2时,求y的值;
(3)当y=3时,求x的值.
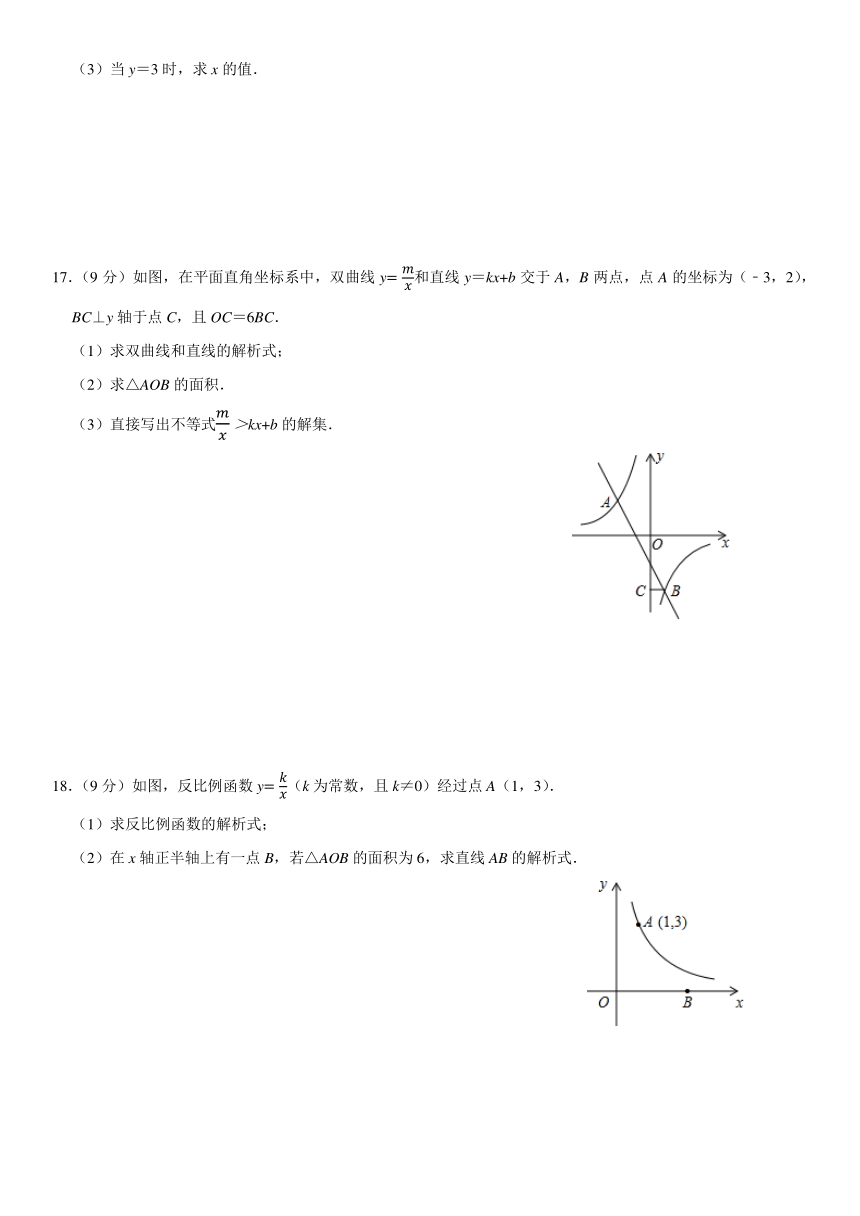
17.(9分)如图,在平面直角坐标系中,双曲线y和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
(1)求双曲线和直线的解析式;
(2)求△AOB的面积.
(3)直接写出不等式kx+b的解集.
18.(9分)如图,反比例函数y(k为常数,且k≠0)经过点A(1,3).
(1)求反比例函数的解析式;
(2)在x轴正半轴上有一点B,若△AOB的面积为6,求直线AB的解析式.
19.(9分)如图,反比例函数y的图象与一次函数y=kx+b的图象交于点A(m,2),点B(﹣2,n),一次函数图象与y轴的交点为C.
(1)求一次函数解析式;
(2)求C点的坐标;
(3)求△AOC的面积.
20.(9分)某企业生产一种必需商品,经过长期市场调查后发现:商品的月总产量稳定在600件.商品的月销量Q(件)由基本销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价x(元/件)(x≤10)成反比例,且可以得到如下信息:
售价x(元/件) 5 8
商品的销售量Q(件) 580 400
(1)求Q与x的函数关系式.
(2)若生产出的商品正好销完,求售价x.
(3)求售价x为多少时,月销售额最大,最大值是多少?
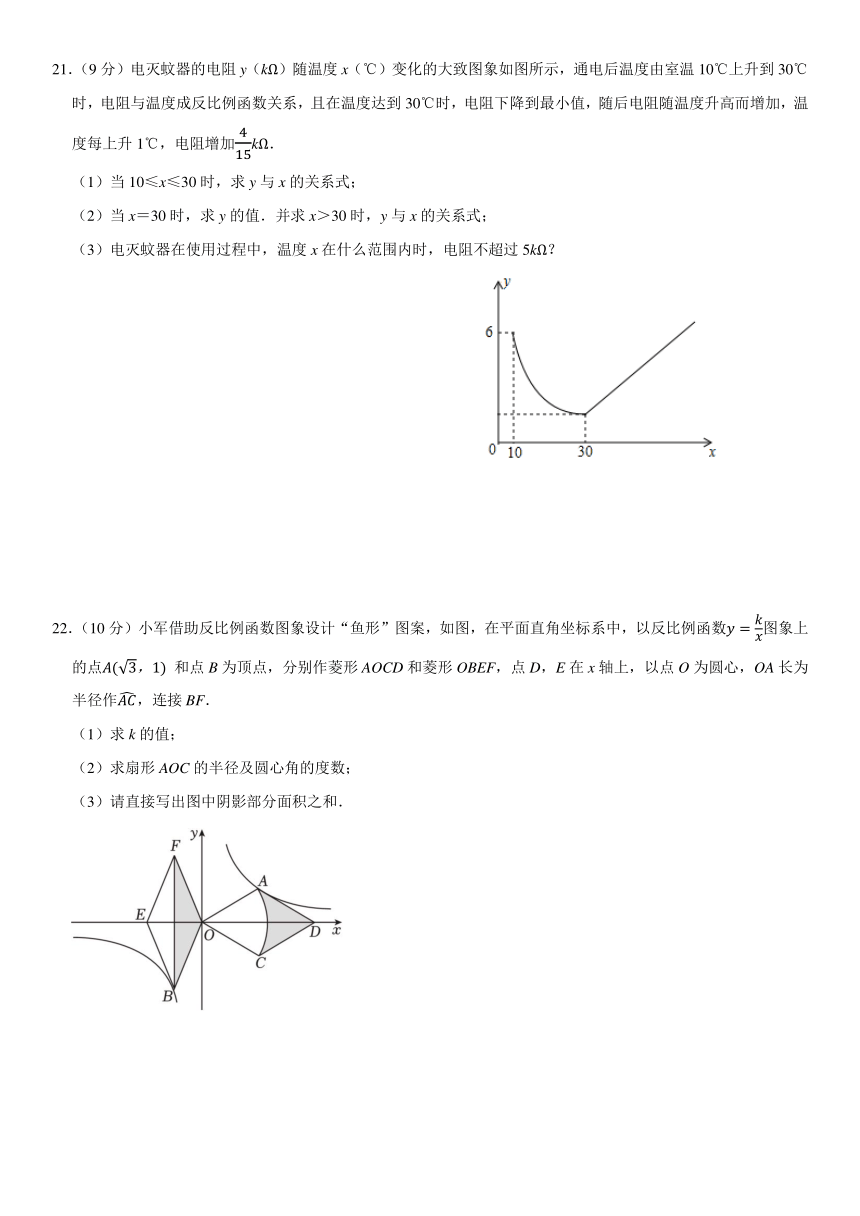
21.(9分)电灭蚊器的电阻y(kΩ)随温度x(℃)变化的大致图象如图所示,通电后温度由室温10℃上升到30℃时,电阻与温度成反比例函数关系,且在温度达到30℃时,电阻下降到最小值,随后电阻随温度升高而增加,温度每上升1℃,电阻增加kΩ.
(1)当10≤x≤30时,求y与x的关系式;
(2)当x=30时,求y的值.并求x>30时,y与x的关系式;
(3)电灭蚊器在使用过程中,温度x在什么范围内时,电阻不超过5kΩ?
22.(10分)小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数图象上的点 和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作,连接BF.
(1)求k的值;
(2)求扇形AOC的半径及圆心角的度数;
(3)请直接写出图中阴影部分面积之和.
23.(11分)如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)点P在y轴上,且满足以点A、O、P为顶点的三角形是等腰三角形,试写出点P所有可能的坐标;
(4)若双曲线上点C(2,n)沿OA方向平移个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵若y=(a+1)x|a|﹣2是反比例函数,
∴|a|﹣2=﹣1且a+1≠0,
解得a=1.
答案为:A.
2.解:∵点P1(x1,y1),P2(x2,y2)在反比例函数y(k>0)的图象上,
∴y1,y2,
∵x1=﹣x2,
∴y1
∴y1=﹣y2.
选:D.
3.解:∵A(﹣1,y1),B(3,y2)两点在双曲线y上,
∴y1=﹣3﹣2m,y2,
∵y1>y2,
∴﹣3﹣2m,
∴m,
选:D.
方法二:
解:由题意可知双曲线位于第二,四象限,
所以3+2m<0,解得m,
选:D.
4.解:∵正比例函数y1与反比例函数y2相交于点E(﹣1,2),
∴根据图象可知当y1>y2>0时x的取值范围是x<﹣1,
∴在数轴上表示为:,
选:A.
5.解:设球内气体的气压P(kPa)和气体体积V(m3)的关系式为P,
∵图象过点(1.6,60),
∴k=96,
即P,在第一象限内,P随V的增大而减小,
∴当P≤120时,V.
选:C.
6.解:过点C作CD⊥OB于点D,如图所示:
在菱形OABC中,OC=BC,
∴OD=BD,
∵菱形OABC的面积为8,点B在y轴的正半轴上,
∴△OCB的面积为4,
∴△OCD的面积为2,
∴2,
∴|k|=4,
∵k<0,
∴k=﹣4,
选:A.
7.解:A、∵m、m+2不同时为零,
∴两直线中总有一条与双曲线相交;
B、当m=1时,点A的坐标为(1,0),点B的坐标为(3,0),
当x=1时,y3,
∴直线l1与双曲线的交点坐标为(1,3);
当x=3时,y1,
∴直线l2与双曲线的交点坐标为(3,1).
∵,
∴当m=1时,两直线与双曲线的交点到原点的距离相等;
C、当﹣2<m<0时,0<m+2<2,
∴当﹣2<m<0时,两直线与双曲线的交点在y轴两侧;
D、∵m+2﹣m=2,且y与x之间一一对应,
∴当两直线与双曲线都有交点时,这两交点的距离大于2.
选:D.
8.解:连接OA、OB,AB交y轴于D,如图,
∵直线y=m平行于x轴,
∴AB∥x轴,
∴S△ABC=S△OAB,
∵S△OBD|﹣2|=1,S△OAD|6|=3,
∴S△OAB=1+3=4,
∴S△ABC=4.
选:C.
9.解:把x=0代入y=kx﹣4得y=﹣4,则B点坐标为(0,﹣4),
∵A为BC的中点,
∴C点的纵坐标为4,
把y=4代入y得x=2,
∴C点坐标为(2,4),
把C(2,4)代入y=kx﹣4得2k﹣4=4,解得k=4,
∴一次函数的表达式为y=4x﹣4,
选:B.
10.解:点P(m,1),点Q(﹣2,n)都在反比例函数y的图象上.
∴m×1=﹣2n=4,
∴m=4,n=﹣2,
∴P(4,1),Q(﹣2,﹣2),
∴S1=4,
作QK⊥PN,交PN的延长线于K,
则PN=4,ON=1,PK=6,KQ=3,
∴S2=S△PQK﹣S△PON﹣S梯形ONKQ(1+3)×2=3,
∴S1:S2=4:3,
选:D.
二.填空题(共5小题,满分15分,每小题3分)
11.解:设这个反比例函数解析式为y,
∴3,
解得k=6,
∴这个反比例函数的解析式是y.
答案为:y.
12.解:∵点A(2,﹣4)在反比例函数y的图象上.
∴k=﹣8,
∴反比例函数解析式为:y,
∵当x=1时,y=﹣8,当x=4时,y=﹣2,
∴当1<x<4时,y的取值范围是:﹣8<y<﹣2.
答案为:﹣8<y<﹣2.
13.解:∵正比例函数的图象与反比例函数y的图象交于A(x1,y1),B(x2,y2)两点,关于原点对称,依此可得x1=﹣x2,y1=﹣y2,
∴(x2﹣x1)(y2﹣y1)
=x2y2﹣x2y1﹣x1y2+x1y1
=x2y2+x2y2+x1y1+x1y1
=6×4
=24.
答案为:24.
14.解:∵正方形OABC的边长为2,
∴B点坐标为(2,2),
当函数y (k≠0)过B点时,k=2×2=4,
∴满足条件的一个反比例函数解析式为y.
答案为:y,y(0<k≤4)(答案不唯一).
15.解:如图∵△AOE的面积为4,函数的图象过一、三象限,
∴S△AOE OE AE=4,
∴OE AE=8,
∴xy=8,
∴k=8,
∵函数y=2x和函数的图象交于A、B两点,
∴2x,
∴x=±2,
当x=2时,y=4,当x=﹣2时,y=﹣4,
∴A、B两点的坐标是:(2,4)(﹣2,﹣4),
∵以点B、O、E、P为顶点的平行四边形共有3个,
∴满足条件的P点有3个,分别为:
P1(0,﹣4),P2(﹣4,﹣4),P3(4,4).
答案为:P1(0,﹣4),P2(﹣4,﹣4),P3(4,4).
三.解答题(共8小题,满分75分)
16.解:(1)把x=3,y=7代入y得:k=21,
则反比例解析式为y,自变量范围为x≠0;
(2)将x=2代入得:y;
(3)将y=3代入得:x=7.
17.解:(1)∵点A(﹣3,2)在双曲线y上,
∴2,即m=﹣6,
∴双曲线的解析式为:y,
∵点B在双曲线y上,且OC=6BC,设点B的坐标为(a,﹣6a),
∴﹣6a,
解得:a=±1(负值舍去),
∴点B的坐标为(1,﹣6),
∵直线y=kx+b过点A,B,
∴,
解得:,
∴直线的解析式为y=﹣2x﹣4;
(2)直线y=﹣2x﹣4交x轴于点D,如图,
把y=0代入y=﹣2x﹣4得﹣2x﹣4=0,
解得x=﹣2,
则D点坐标为(﹣2,0),
△AOB的面积=S△AOD+S△BOD
2×22×6
=8.
(3)根据图象得:不等式kx+b的解集为﹣3<x<0或x>1.
18.解:(1)∵反比例函数y(k为常数,且k≠0)经过点A(1,3),
∴3,
解得:k=3,
∴反比例函数解析式为y;
(2)设B(a,0),则BO=a,
∵△AOB的面积为6,
∴ a 3=6,
解得:a=4,
∴B(4,0),
设直线AB的解析式为y=kx+b,
∵经过A(1,3),B(4,0),
∴,
解得,
∴直线AB的解析式为y=﹣x+4.
19.解:(1)由题意,把A(m,2),B(﹣2,n)代入中,得,
∴A(1,2),B(﹣2,﹣1)将A、B代入y=kx+b中得:
,∴,
∴一次函数解析式为:y=x+1;
(2)由(1)可知:当x=0时,y=1,
∴C(0,1);
(3)S△AOC1×1.
20.解:(1)设Q=a,
由表格可知:当x=5时,Q=580,当x=8时,Q=400,
∴,
解得,
即Q与x的函数关系式是Q=100;
(2)令Q=600,
600=100,
解得x=4.8,
答:生产出的商品正好销完,此时x的值是4.8;
(3)设月销售额为w元,
由题意可得,w=x(100)=100x+2400,
∴w随x的增大而增大,
∵x≤10,
∴当x=10时,w取得最大值,此时w=3400,
答:售价x为10时,月销售额最大,最大值是3400元.
21.解:(1)设y.
∵过点(10,6),
∴m=xy=10×6=60.
∴当10≤x≤30时,y与x的关系式为:;
(2)∵,
∴当x=30时,.
x>30时,设y=kx+b,
∵过点(30,2),
∵温度每上升1℃,电阻增加.
∴过点,
∴,
解得:,
y与x的关系式为:;
(3),当y=5时,得x=12;
,当y=5时,得;
答:温度x取值范围是.
22.解:(1)将A(,1)代入到y中,
得:1,
解得:k;
(2)过点A作OD 的垂线,交x轴于G,
∵A(,1),
∴AG=1,OG,
OA2,
∴半径为2;
∵AGOA,
∴∠AOG=30°,
由菱形的性质可知,∠AOG=∠COG=30°,
∴∠AOC=60°,
∴圆心角的度数为:60°;
(3)∵OD=2OG=2,
∴S菱形AOCDAC×OD=2,
∴S扇形AOCπ×r2,
在菱形OBEF中,S△FHO=S△BHO,
∵S△FHO,
∴S△FBO=2,
∴S阴影=S△FBO+S菱形AOCD﹣S扇形AOC2π=3.
23.解:(1)设反比例函数的解析式为y(k>0),
∵A(m,﹣2)在y=2x上,
∴﹣2=2m,
∴m=﹣1,
∴A(﹣1,﹣2),
又点A在y上,
∴﹣2,
∴k=2,
∴反比例函数的解析式为y;
(2)由A的坐标为(﹣1,﹣2),得到D(1,2),
由图象得:正比例函数值大于反比例函数值时自变量x的取值范围为﹣1<x<0或x>1;
(3)OA,分三种情形:
①以O为顶点,P1(O,),P2(O,);
②以A为顶点,P3(O,﹣4);
③以OA为底边,设P4(O,﹣b),OA中点为D,连接DP4、AP4,
∵S△OAP4OP4|xA|OA DP4,
∴DP4,
在Rt△ODP4中,由勾股定理得:OD2+DP42=OP42,
∴b,
∴P4(O,);
(4)四边形OABC是菱形,理由为:
证明:∵A(﹣1,﹣2),
∴OA,
由题意知:CB∥OA且CB,
∴CB=OA,
∴四边形OABC是平行四边形,
∵C(2,n)在y上,
∴n=1,
∴C(2,1),
∴OC,
∴OC=OA,
∴四边形OABC是菱形.
考试范围:第26章 反比例函数;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.若y=(a+1)x|a|﹣2是反比例函数,则a的取值为( )
A.1 B.﹣1 C.±1 D.任意实数
2.若点P1(x1,y1),P2(x2,y2)在反比例函数y(k>0)的图象上,且x1=﹣x2,则( )
A.y1<y2 B.y1=y2 C.y1>y2 D.y1=﹣y2
3.已知A(﹣1,y1),B(3,y2)两点在双曲线y上,且y1>y2,则m的取值范围是( )
A.m<0 B.m>0 C.m D.m
4.如图,正比例函数y1与反比例函数y2相交于点E(﹣1,2),若y1>y2>0,则x的取值范围在数轴上表示正确的是( )
A. B.
C. D.
5.某种气球内充满了一定质量的气体,当温度不变时,气球内的气体的气压P(kPa)是气球体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将爆炸,为了安全,气球的体积应该( )
A.不大于m3 B.小于m3
C.不小于m3 D.小于m3
6.如图,点B在y轴的正半轴上,点C在反比例函数y(x<0)的图象上,菱形OABC的面积为8,则k的值为( )
A.﹣4 B.4 C.﹣2 D.2
7.在平面直角坐标系中,分别过点A(m,0),B(m+2,0)作x轴的垂线l1和l2,探究直线l1,直线l2与双曲线y的关系,下列结论中错误的是( )
A.两直线中总有一条与双曲线相交
B.当m=1时,两直线与双曲线的交点到原点的距离相等
C.当﹣2<m<0时,两直线与双曲线的交点在y轴两侧
D.当两直线与双曲线都有交点时,这两交点的最短距离是2
8.如图,直线y=m与反比例函数和的图象分别交于A、B两点,点C是x轴上任意一点,则△ABC的面积为( )
A.1 B.3 C.4 D.8
9.如图,已知一次函数y=kx﹣4的图象与x轴,y轴分别交于A,B两点,与反比例函数y在第一象限内的图象交于点C,且A为BC的中点,则一次函数的解析式为( )
A.y=2x﹣4 B.y=4x﹣4 C.y=8x﹣4 D.y=16x﹣4
10.如图,点P(m,1),点Q(﹣2,n)都在反比例函数的图象上.过点P分别向x轴、y轴作垂线,垂足分别为点M,N.连接OP,OQ,PQ.若四边形OMPN的面积记作S1,△POQ的面积记作S2,则( )
A.S1:S2=2:3 B.S1:S2=1:1 C.S1:S2=4:1 D.S1:S2=4:3
(8题图) (9题图) (10题图) (14题图)
二.填空题(共5小题,满分15分,每小题3分)
11.一个反比例函数图象过点A(﹣2,﹣3),则这个反比例函数的解析式是 .
12.已知点A(2,﹣4)在反比例函数y的图象上.当1<x<4时,y的取值范围是 .
13.如果一个正比例函数的图象与反比例函数y的图象交于A(x1,y1),B(x2,y2)两点,那么(x2﹣x1)(y2﹣y1)的值为 .
14.如图,在平面直角坐标系xOy中,正方形OABC的边长为2.写出一个函数y(k≠0),使它的图象与正方形OABC有公共点,这个函数的表达式为 .
15.如图,已知函数y=2x和函数的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,则满足条件的P点坐标是 .
三.解答题(共8小题,满分75分)
16.(9分)已知y与x成反比例,并且x=3时,y=7.
(1)写出这个函数的解析式和自变量的取值范围;
(2)当x=2时,求y的值;
(3)当y=3时,求x的值.
17.(9分)如图,在平面直角坐标系中,双曲线y和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
(1)求双曲线和直线的解析式;
(2)求△AOB的面积.
(3)直接写出不等式kx+b的解集.
18.(9分)如图,反比例函数y(k为常数,且k≠0)经过点A(1,3).
(1)求反比例函数的解析式;
(2)在x轴正半轴上有一点B,若△AOB的面积为6,求直线AB的解析式.
19.(9分)如图,反比例函数y的图象与一次函数y=kx+b的图象交于点A(m,2),点B(﹣2,n),一次函数图象与y轴的交点为C.
(1)求一次函数解析式;
(2)求C点的坐标;
(3)求△AOC的面积.
20.(9分)某企业生产一种必需商品,经过长期市场调查后发现:商品的月总产量稳定在600件.商品的月销量Q(件)由基本销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价x(元/件)(x≤10)成反比例,且可以得到如下信息:
售价x(元/件) 5 8
商品的销售量Q(件) 580 400
(1)求Q与x的函数关系式.
(2)若生产出的商品正好销完,求售价x.
(3)求售价x为多少时,月销售额最大,最大值是多少?
21.(9分)电灭蚊器的电阻y(kΩ)随温度x(℃)变化的大致图象如图所示,通电后温度由室温10℃上升到30℃时,电阻与温度成反比例函数关系,且在温度达到30℃时,电阻下降到最小值,随后电阻随温度升高而增加,温度每上升1℃,电阻增加kΩ.
(1)当10≤x≤30时,求y与x的关系式;
(2)当x=30时,求y的值.并求x>30时,y与x的关系式;
(3)电灭蚊器在使用过程中,温度x在什么范围内时,电阻不超过5kΩ?
22.(10分)小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数图象上的点 和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作,连接BF.
(1)求k的值;
(2)求扇形AOC的半径及圆心角的度数;
(3)请直接写出图中阴影部分面积之和.
23.(11分)如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)点P在y轴上,且满足以点A、O、P为顶点的三角形是等腰三角形,试写出点P所有可能的坐标;
(4)若双曲线上点C(2,n)沿OA方向平移个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵若y=(a+1)x|a|﹣2是反比例函数,
∴|a|﹣2=﹣1且a+1≠0,
解得a=1.
答案为:A.
2.解:∵点P1(x1,y1),P2(x2,y2)在反比例函数y(k>0)的图象上,
∴y1,y2,
∵x1=﹣x2,
∴y1
∴y1=﹣y2.
选:D.
3.解:∵A(﹣1,y1),B(3,y2)两点在双曲线y上,
∴y1=﹣3﹣2m,y2,
∵y1>y2,
∴﹣3﹣2m,
∴m,
选:D.
方法二:
解:由题意可知双曲线位于第二,四象限,
所以3+2m<0,解得m,
选:D.
4.解:∵正比例函数y1与反比例函数y2相交于点E(﹣1,2),
∴根据图象可知当y1>y2>0时x的取值范围是x<﹣1,
∴在数轴上表示为:,
选:A.
5.解:设球内气体的气压P(kPa)和气体体积V(m3)的关系式为P,
∵图象过点(1.6,60),
∴k=96,
即P,在第一象限内,P随V的增大而减小,
∴当P≤120时,V.
选:C.
6.解:过点C作CD⊥OB于点D,如图所示:
在菱形OABC中,OC=BC,
∴OD=BD,
∵菱形OABC的面积为8,点B在y轴的正半轴上,
∴△OCB的面积为4,
∴△OCD的面积为2,
∴2,
∴|k|=4,
∵k<0,
∴k=﹣4,
选:A.
7.解:A、∵m、m+2不同时为零,
∴两直线中总有一条与双曲线相交;
B、当m=1时,点A的坐标为(1,0),点B的坐标为(3,0),
当x=1时,y3,
∴直线l1与双曲线的交点坐标为(1,3);
当x=3时,y1,
∴直线l2与双曲线的交点坐标为(3,1).
∵,
∴当m=1时,两直线与双曲线的交点到原点的距离相等;
C、当﹣2<m<0时,0<m+2<2,
∴当﹣2<m<0时,两直线与双曲线的交点在y轴两侧;
D、∵m+2﹣m=2,且y与x之间一一对应,
∴当两直线与双曲线都有交点时,这两交点的距离大于2.
选:D.
8.解:连接OA、OB,AB交y轴于D,如图,
∵直线y=m平行于x轴,
∴AB∥x轴,
∴S△ABC=S△OAB,
∵S△OBD|﹣2|=1,S△OAD|6|=3,
∴S△OAB=1+3=4,
∴S△ABC=4.
选:C.
9.解:把x=0代入y=kx﹣4得y=﹣4,则B点坐标为(0,﹣4),
∵A为BC的中点,
∴C点的纵坐标为4,
把y=4代入y得x=2,
∴C点坐标为(2,4),
把C(2,4)代入y=kx﹣4得2k﹣4=4,解得k=4,
∴一次函数的表达式为y=4x﹣4,
选:B.
10.解:点P(m,1),点Q(﹣2,n)都在反比例函数y的图象上.
∴m×1=﹣2n=4,
∴m=4,n=﹣2,
∴P(4,1),Q(﹣2,﹣2),
∴S1=4,
作QK⊥PN,交PN的延长线于K,
则PN=4,ON=1,PK=6,KQ=3,
∴S2=S△PQK﹣S△PON﹣S梯形ONKQ(1+3)×2=3,
∴S1:S2=4:3,
选:D.
二.填空题(共5小题,满分15分,每小题3分)
11.解:设这个反比例函数解析式为y,
∴3,
解得k=6,
∴这个反比例函数的解析式是y.
答案为:y.
12.解:∵点A(2,﹣4)在反比例函数y的图象上.
∴k=﹣8,
∴反比例函数解析式为:y,
∵当x=1时,y=﹣8,当x=4时,y=﹣2,
∴当1<x<4时,y的取值范围是:﹣8<y<﹣2.
答案为:﹣8<y<﹣2.
13.解:∵正比例函数的图象与反比例函数y的图象交于A(x1,y1),B(x2,y2)两点,关于原点对称,依此可得x1=﹣x2,y1=﹣y2,
∴(x2﹣x1)(y2﹣y1)
=x2y2﹣x2y1﹣x1y2+x1y1
=x2y2+x2y2+x1y1+x1y1
=6×4
=24.
答案为:24.
14.解:∵正方形OABC的边长为2,
∴B点坐标为(2,2),
当函数y (k≠0)过B点时,k=2×2=4,
∴满足条件的一个反比例函数解析式为y.
答案为:y,y(0<k≤4)(答案不唯一).
15.解:如图∵△AOE的面积为4,函数的图象过一、三象限,
∴S△AOE OE AE=4,
∴OE AE=8,
∴xy=8,
∴k=8,
∵函数y=2x和函数的图象交于A、B两点,
∴2x,
∴x=±2,
当x=2时,y=4,当x=﹣2时,y=﹣4,
∴A、B两点的坐标是:(2,4)(﹣2,﹣4),
∵以点B、O、E、P为顶点的平行四边形共有3个,
∴满足条件的P点有3个,分别为:
P1(0,﹣4),P2(﹣4,﹣4),P3(4,4).
答案为:P1(0,﹣4),P2(﹣4,﹣4),P3(4,4).
三.解答题(共8小题,满分75分)
16.解:(1)把x=3,y=7代入y得:k=21,
则反比例解析式为y,自变量范围为x≠0;
(2)将x=2代入得:y;
(3)将y=3代入得:x=7.
17.解:(1)∵点A(﹣3,2)在双曲线y上,
∴2,即m=﹣6,
∴双曲线的解析式为:y,
∵点B在双曲线y上,且OC=6BC,设点B的坐标为(a,﹣6a),
∴﹣6a,
解得:a=±1(负值舍去),
∴点B的坐标为(1,﹣6),
∵直线y=kx+b过点A,B,
∴,
解得:,
∴直线的解析式为y=﹣2x﹣4;
(2)直线y=﹣2x﹣4交x轴于点D,如图,
把y=0代入y=﹣2x﹣4得﹣2x﹣4=0,
解得x=﹣2,
则D点坐标为(﹣2,0),
△AOB的面积=S△AOD+S△BOD
2×22×6
=8.
(3)根据图象得:不等式kx+b的解集为﹣3<x<0或x>1.
18.解:(1)∵反比例函数y(k为常数,且k≠0)经过点A(1,3),
∴3,
解得:k=3,
∴反比例函数解析式为y;
(2)设B(a,0),则BO=a,
∵△AOB的面积为6,
∴ a 3=6,
解得:a=4,
∴B(4,0),
设直线AB的解析式为y=kx+b,
∵经过A(1,3),B(4,0),
∴,
解得,
∴直线AB的解析式为y=﹣x+4.
19.解:(1)由题意,把A(m,2),B(﹣2,n)代入中,得,
∴A(1,2),B(﹣2,﹣1)将A、B代入y=kx+b中得:
,∴,
∴一次函数解析式为:y=x+1;
(2)由(1)可知:当x=0时,y=1,
∴C(0,1);
(3)S△AOC1×1.
20.解:(1)设Q=a,
由表格可知:当x=5时,Q=580,当x=8时,Q=400,
∴,
解得,
即Q与x的函数关系式是Q=100;
(2)令Q=600,
600=100,
解得x=4.8,
答:生产出的商品正好销完,此时x的值是4.8;
(3)设月销售额为w元,
由题意可得,w=x(100)=100x+2400,
∴w随x的增大而增大,
∵x≤10,
∴当x=10时,w取得最大值,此时w=3400,
答:售价x为10时,月销售额最大,最大值是3400元.
21.解:(1)设y.
∵过点(10,6),
∴m=xy=10×6=60.
∴当10≤x≤30时,y与x的关系式为:;
(2)∵,
∴当x=30时,.
x>30时,设y=kx+b,
∵过点(30,2),
∵温度每上升1℃,电阻增加.
∴过点,
∴,
解得:,
y与x的关系式为:;
(3),当y=5时,得x=12;
,当y=5时,得;
答:温度x取值范围是.
22.解:(1)将A(,1)代入到y中,
得:1,
解得:k;
(2)过点A作OD 的垂线,交x轴于G,
∵A(,1),
∴AG=1,OG,
OA2,
∴半径为2;
∵AGOA,
∴∠AOG=30°,
由菱形的性质可知,∠AOG=∠COG=30°,
∴∠AOC=60°,
∴圆心角的度数为:60°;
(3)∵OD=2OG=2,
∴S菱形AOCDAC×OD=2,
∴S扇形AOCπ×r2,
在菱形OBEF中,S△FHO=S△BHO,
∵S△FHO,
∴S△FBO=2,
∴S阴影=S△FBO+S菱形AOCD﹣S扇形AOC2π=3.
23.解:(1)设反比例函数的解析式为y(k>0),
∵A(m,﹣2)在y=2x上,
∴﹣2=2m,
∴m=﹣1,
∴A(﹣1,﹣2),
又点A在y上,
∴﹣2,
∴k=2,
∴反比例函数的解析式为y;
(2)由A的坐标为(﹣1,﹣2),得到D(1,2),
由图象得:正比例函数值大于反比例函数值时自变量x的取值范围为﹣1<x<0或x>1;
(3)OA,分三种情形:
①以O为顶点,P1(O,),P2(O,);
②以A为顶点,P3(O,﹣4);
③以OA为底边,设P4(O,﹣b),OA中点为D,连接DP4、AP4,
∵S△OAP4OP4|xA|OA DP4,
∴DP4,
在Rt△ODP4中,由勾股定理得:OD2+DP42=OP42,
∴b,
∴P4(O,);
(4)四边形OABC是菱形,理由为:
证明:∵A(﹣1,﹣2),
∴OA,
由题意知:CB∥OA且CB,
∴CB=OA,
∴四边形OABC是平行四边形,
∵C(2,n)在y上,
∴n=1,
∴C(2,1),
∴OC,
∴OC=OA,
∴四边形OABC是菱形.
