人教版 八年级数学 第十一章 三角形 练习卷(含答案)
文档属性
| 名称 | 人教版 八年级数学 第十一章 三角形 练习卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 831.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-04 21:03:38 | ||
图片预览



文档简介
2024-2025学年第一学期甘肃省武威市八年级
数学人教版第十一章《三角形》练习卷
一、单选题
1.下列长度的三条线段,不能组成三角形的是( )
A.4,3,4 B.6,8,10 C.5,6,12 D.6,6,6
2.点是和的平分线的交点.若,则的度数为( )
A. B. C. D.
3.如图,在中,,点分别在上,则的度数为( )
A. B. C. D.
4.如图,在中,,,分别是,,的中点,,则阴影部分的面积等于( )
A. B. C. D.
5.如图,一轮船在海上往东行驶,在处测得灯塔位于北偏东,在处测得灯塔位于北偏东,则()
A. B. C. D.
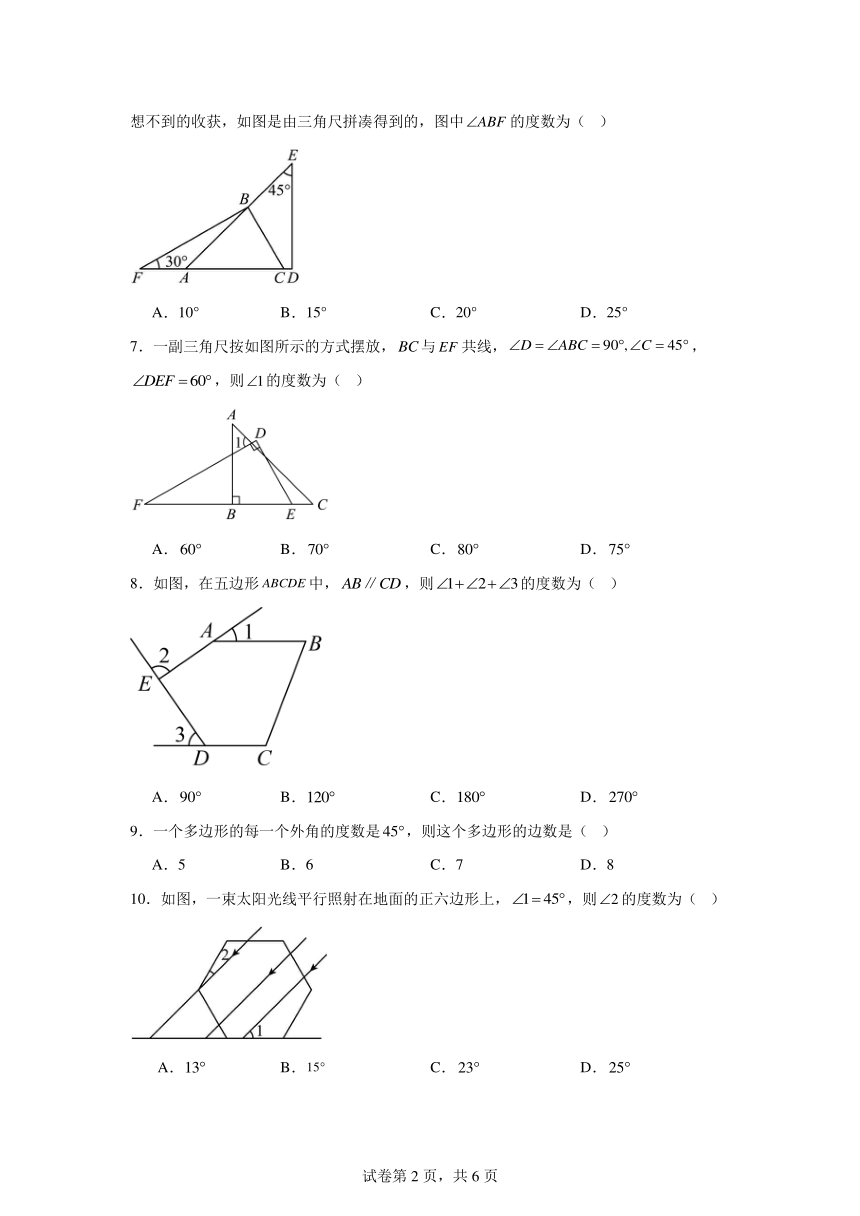
6.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图是由三角尺拼凑得到的,图中的度数为( )
A.10° B.15° C.20° D.25°
7.一副三角尺按如图所示的方式摆放,与共线,,,则的度数为( )
A. B. C. D.
8.如图,在五边形中,,则的度数为( )
A. B. C. D.
9.一个多边形的每一个外角的度数是,则这个多边形的边数是( )
A.5 B.6 C.7 D.8
10.如图,一束太阳光线平行照射在地面的正六边形上,,则的度数为( )
A. B. C. D.
二、填空题
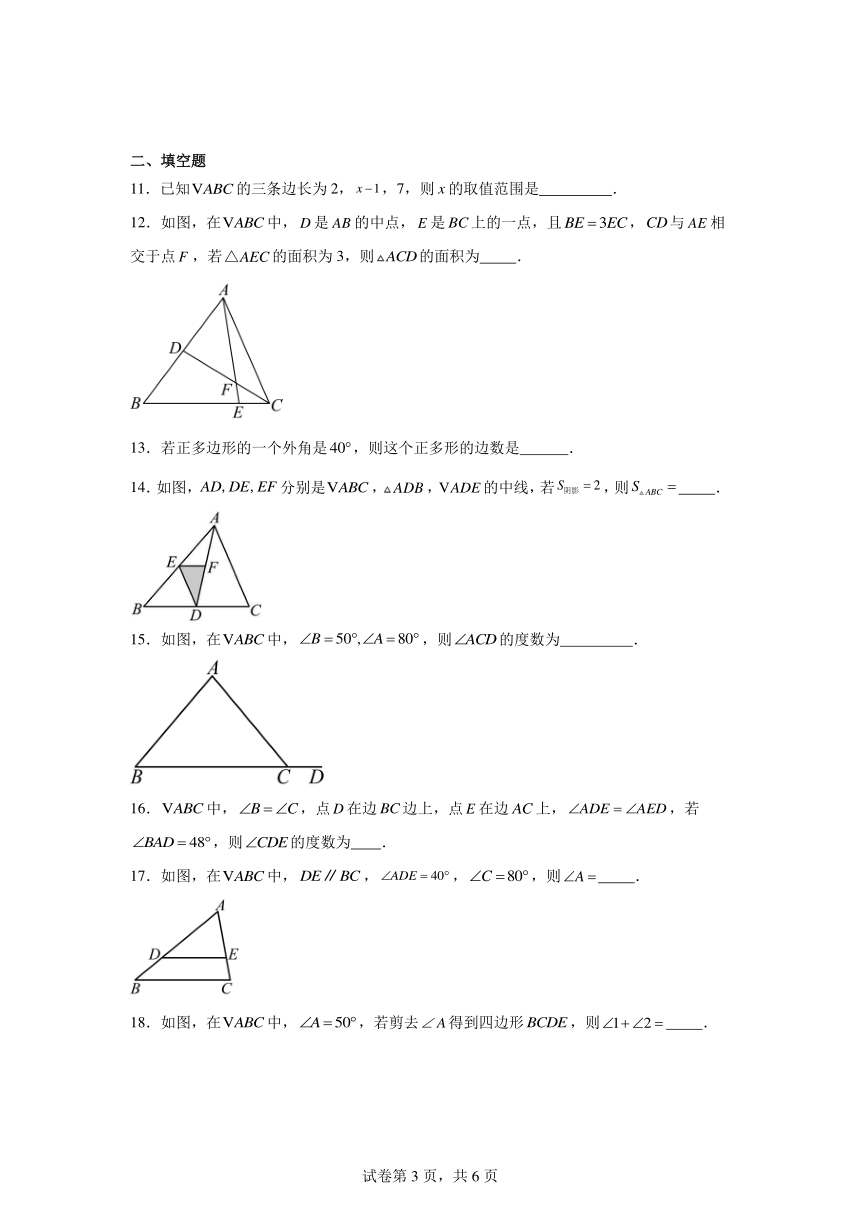
11.已知的三条边长为2,,7,则x的取值范围是 .
12.如图,在中,是的中点,是上的一点,且,与相交于点,若的面积为3,则的面积为 .
13.若正多边形的一个外角是,则这个正多形的边数是 .
14.如图,分别是,,的中线,若,则 .
15.如图,在中,,则的度数为 .
16.中,,点在边边上,点在边上,,若,则的度数为 .
17.如图,在中,,,,则 .
18.如图,在中,,若剪去得到四边形,则 .
三、解答题
19.如图,为的中线,为的中线,为中边上的高.若的面积为24,,求的长.
20.已知一个多边形每个内角的度数都为,求这个多边形的内角和.
21.已知的三边长是.
(1)若,,且三角形的周长是小于22的偶数,求的值;
(2)化简:.
22.在中,,.
(1)若是偶数,求的长;
(2)已知是的中线,若的周长为10,求的周长.
23.如图,在中,,,.
(1)求的度数;
(2)若,求的度数.
24.如图,在中,是边上的高,,,
(1)若是的角平分线,求的度数;
(2)若是的中线,的周长比的周长大1且,,求的长度.
25.如图,在四边形中,已知,平分,平分.
(1)求的度数;
(2)求证:.
26.在四边形中,的平分线交边于点,的平分线交直线于点.
(1)当点O在四边形的内部时.如图①,若,,,则 °,
(2)如图②,试探索、和之间的数量关系,并说明理由;
(3)如图③,当点在四边形的外部时,请你直接写出、和之间的数量关系.
27.已知中,
(1)如图1,平分,平分,,求的度数;
(2)如图2,是的外角,、的平分线交于点D,求与的数量关系;
(3)如图3,、是的外角,的平分线所在的直线与、的平分线分别交于点F D.在中,如果,求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A C B B D C D B
11.
12.6
13.九/9
14.16
15./130度
16.24°
17./60度
18./230度
19.
20.
21.(1)解:是的三边,,,
.
三角形的周长是小于22的偶数,
,
或;
(2)解:是的三边,
,,
∴.
22.(1)解:由题意得:,
又,,
,
又是偶数,
;
(2)解:是的中线,
.
的周长为10,
,
,
,
,
又,
的周长.
23.(1)解:,,,
,
,
;
(2)解:,,
,
,
.
24.(1)解:∵,,
∴,
∵是的角平分线,是的高,
∴,,
∴.
(2)解:∵是的中线,
∴,
∵已知的周长比的周长大1,即,
∴,
∵,
∴;
∵,,,,,
∴,
即,
∴.
25.(1)解:∵,,
∴;
(2)证明:设,
∵平分,
∴,
∵
∴,
∵平分,
∴,
∴在中,,
∴,
∴.
26.(1)解:,
,,
,,
,,
的平分线交边于点,的平分线交直线于点,
,,
,
故答案为:125.
(2)解:,理由如下:
,
,,
,,
的平分线交边于点,的平分线交直线于点,
,,
,
.
(3)解:,理由如下:
的平分线交边于点,的平分线交直线于点,
,,
在四边形中,
,
,
,
,
.
27.(1)解:,,
,
平分,平分,
,,
,
,
;
(2)解:如图,设与交于点,
、分别是、的平分线,
,,
,
,
;
(3)解:平分,平分,
,,
,
平分,平分,
∴由(2)可知:,
,
,
,
.
答案第1页,共2页
答案第1页,共2页
数学人教版第十一章《三角形》练习卷
一、单选题
1.下列长度的三条线段,不能组成三角形的是( )
A.4,3,4 B.6,8,10 C.5,6,12 D.6,6,6
2.点是和的平分线的交点.若,则的度数为( )
A. B. C. D.
3.如图,在中,,点分别在上,则的度数为( )
A. B. C. D.
4.如图,在中,,,分别是,,的中点,,则阴影部分的面积等于( )
A. B. C. D.
5.如图,一轮船在海上往东行驶,在处测得灯塔位于北偏东,在处测得灯塔位于北偏东,则()
A. B. C. D.
6.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图是由三角尺拼凑得到的,图中的度数为( )
A.10° B.15° C.20° D.25°
7.一副三角尺按如图所示的方式摆放,与共线,,,则的度数为( )
A. B. C. D.
8.如图,在五边形中,,则的度数为( )
A. B. C. D.
9.一个多边形的每一个外角的度数是,则这个多边形的边数是( )
A.5 B.6 C.7 D.8
10.如图,一束太阳光线平行照射在地面的正六边形上,,则的度数为( )
A. B. C. D.
二、填空题
11.已知的三条边长为2,,7,则x的取值范围是 .
12.如图,在中,是的中点,是上的一点,且,与相交于点,若的面积为3,则的面积为 .
13.若正多边形的一个外角是,则这个正多形的边数是 .
14.如图,分别是,,的中线,若,则 .
15.如图,在中,,则的度数为 .
16.中,,点在边边上,点在边上,,若,则的度数为 .
17.如图,在中,,,,则 .
18.如图,在中,,若剪去得到四边形,则 .
三、解答题
19.如图,为的中线,为的中线,为中边上的高.若的面积为24,,求的长.
20.已知一个多边形每个内角的度数都为,求这个多边形的内角和.
21.已知的三边长是.
(1)若,,且三角形的周长是小于22的偶数,求的值;
(2)化简:.
22.在中,,.
(1)若是偶数,求的长;
(2)已知是的中线,若的周长为10,求的周长.
23.如图,在中,,,.
(1)求的度数;
(2)若,求的度数.
24.如图,在中,是边上的高,,,
(1)若是的角平分线,求的度数;
(2)若是的中线,的周长比的周长大1且,,求的长度.
25.如图,在四边形中,已知,平分,平分.
(1)求的度数;
(2)求证:.
26.在四边形中,的平分线交边于点,的平分线交直线于点.
(1)当点O在四边形的内部时.如图①,若,,,则 °,
(2)如图②,试探索、和之间的数量关系,并说明理由;
(3)如图③,当点在四边形的外部时,请你直接写出、和之间的数量关系.
27.已知中,
(1)如图1,平分,平分,,求的度数;
(2)如图2,是的外角,、的平分线交于点D,求与的数量关系;
(3)如图3,、是的外角,的平分线所在的直线与、的平分线分别交于点F D.在中,如果,求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A C B B D C D B
11.
12.6
13.九/9
14.16
15./130度
16.24°
17./60度
18./230度
19.
20.
21.(1)解:是的三边,,,
.
三角形的周长是小于22的偶数,
,
或;
(2)解:是的三边,
,,
∴.
22.(1)解:由题意得:,
又,,
,
又是偶数,
;
(2)解:是的中线,
.
的周长为10,
,
,
,
,
又,
的周长.
23.(1)解:,,,
,
,
;
(2)解:,,
,
,
.
24.(1)解:∵,,
∴,
∵是的角平分线,是的高,
∴,,
∴.
(2)解:∵是的中线,
∴,
∵已知的周长比的周长大1,即,
∴,
∵,
∴;
∵,,,,,
∴,
即,
∴.
25.(1)解:∵,,
∴;
(2)证明:设,
∵平分,
∴,
∵
∴,
∵平分,
∴,
∴在中,,
∴,
∴.
26.(1)解:,
,,
,,
,,
的平分线交边于点,的平分线交直线于点,
,,
,
故答案为:125.
(2)解:,理由如下:
,
,,
,,
的平分线交边于点,的平分线交直线于点,
,,
,
.
(3)解:,理由如下:
的平分线交边于点,的平分线交直线于点,
,,
在四边形中,
,
,
,
,
.
27.(1)解:,,
,
平分,平分,
,,
,
,
;
(2)解:如图,设与交于点,
、分别是、的平分线,
,,
,
,
;
(3)解:平分,平分,
,,
,
平分,平分,
∴由(2)可知:,
,
,
,
.
答案第1页,共2页
答案第1页,共2页
