勾股定理的应用
图片预览




文档简介
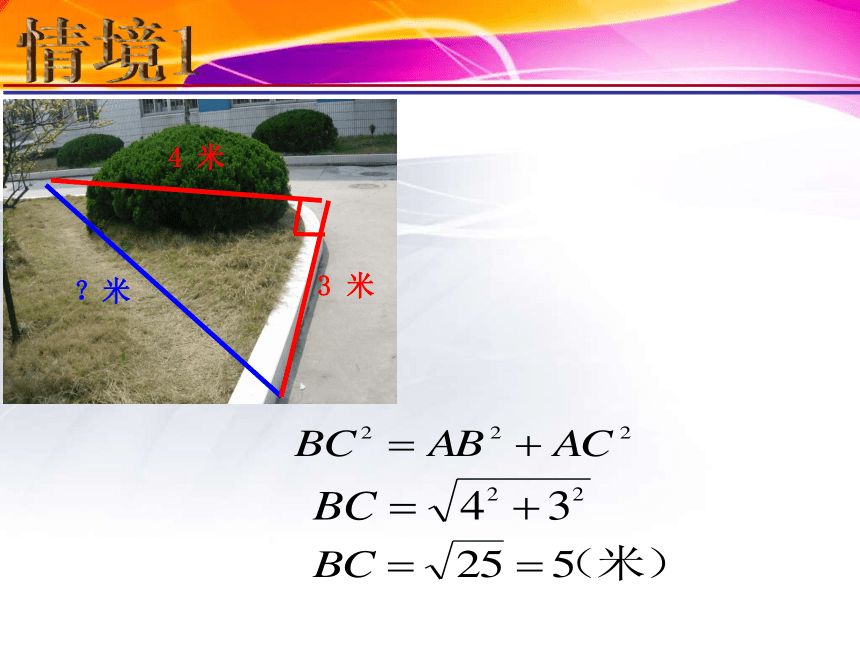
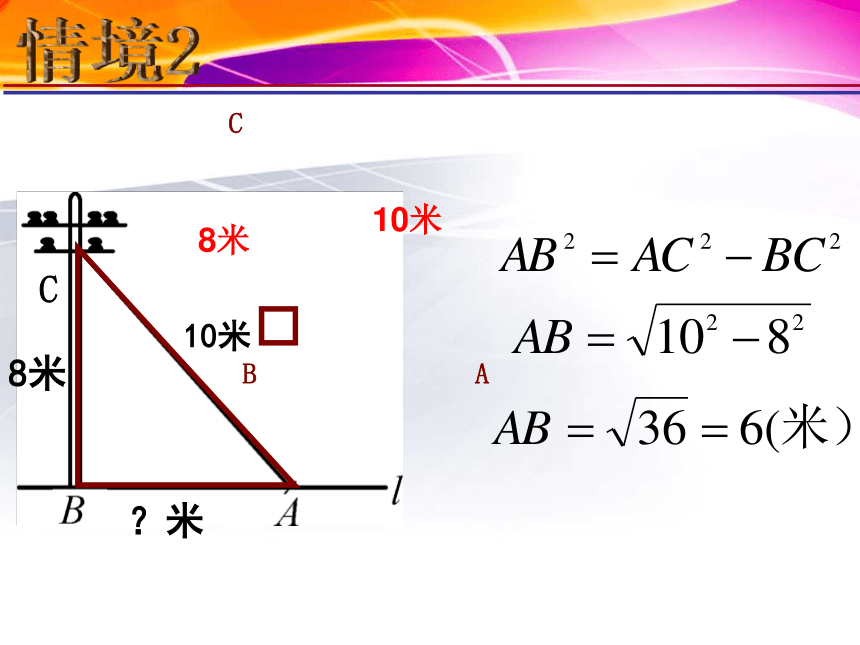
课件19张PPT。数学源于生活 又服务于生活石洞中学 舒守炎情境1?米情境1情境28米10米BAC请回忆直角边的平方和
斜边的平方.勾股定理的应用 学习目标
1、知识与技能
通过对一些实际问题的探究,能运用勾股定理解决一些简单的实际问题.
2、过程与方法
积极参与勾股定理的应用过程,熟练掌握其应用方法,明确应用的条件.通过练习、巩固知识、拓展知识.
3、情感、态度与价值观
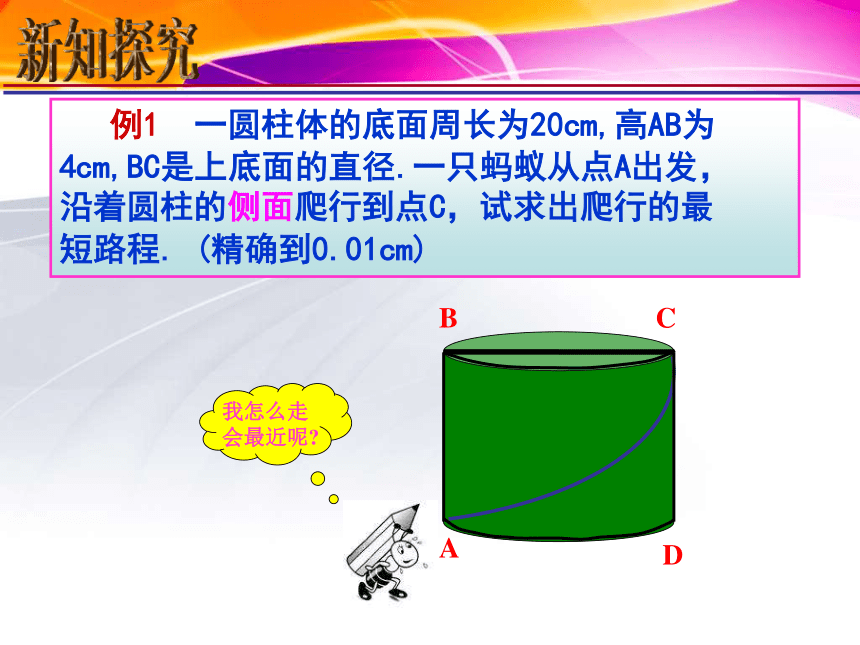
培养自己的合情推理能力,体会数形结合的思维方法.提高学习热情,感受数学源于生活又服务于生活.新知探究 例1 一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,
沿着圆柱的侧面爬行到点C,试求出爬行的最
短路程. (精确到0.01cm) 新知探究4cm周长的一半答:最短路程约为10.77cm.4cm底面周长20cm变形练习 在灯罩的侧面从底部到顶部缠绕了一圈金黄色纸带作为装饰.如图灯罩的高为30cm,其底部周长为40cm,他们要剪裁纸带的长度至少为多少cm?? 一辆高2.2米,宽2米的卡车要通过一个半径为3米的半圆形隧道,它能顺利通过吗?OA1mCBD.分析:隧道宽度是足够的,所以卡车能否通过,只要看卡车位于隧道正中间时其高度是否小于( ).?
因为2.8>2.2,高度上有0.6米的余量,所以卡车能通过隧道.新知探究CD连接OD,得到RtΔOCD如何求CD呢?解:在RtΔOCD中,由勾股
定理得3m 例2 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如下图的某工厂,问这辆卡车能否通过该工厂的厂门?变形练习分析:
1、厂门的宽度足够,所以卡车能否通过,只要看卡车位于厂门正中间时,其高度是否小于( ),要求CH就必须先求( ),而要求出CD我们可以建立RtΔ( )。
2、在RtΔOCD中,直角边OD=( )
斜边OC=( )
CHCDOCD1米0.8米CH = 0.6+2.3 = 2.9>2.5 因此高度上有0.4米的余量,所以卡车能通过厂门.0.8m1m方法归纳应用勾股定理的解题思路:
从实际问题中直角三角形,运用勾股定理解决.达标反馈现准备将一块形为直角三角形的绿地扩大,使其仍为直角三角形,两直角边同时扩大到原来的两倍,问斜边扩大到原来的多少倍?解:在RtΔABC中,根据勾股定理得符合题意.2a2b所以,斜边扩大2倍符合题意.中考链接 如果将例1的圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面从点A到点B需要爬行的最短路程又是多少呢?10cm20cm拓展延伸 我家附近有棵8米高的大树,在一个雷雨天被雷电击中断裂,树的顶部落在离树根底部4米的地方,你能计算出原处的大树还有多高吗?4米ABCABC(应用勾股定理列方程)类似:教材《九章算术》
折竹抵地4米谈谈我们的收获……课堂小结我学会了……
我明白了……
我会用……
通过本节课的研究,作业:1 教材习题14.2 第1、2、3题
2 在生活中需找可以运用勾股定理解决的实际问题,并写下来予以解决.如果将例1的圆柱体换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面从点A到点B需要爬行的最短路程又是多少呢?课后思考生活中的数学无处不在
希望同学们善于
用数学的视角观察世界
用数学的思维理解世界
发现生活中的数学
惊奇和趣味也许就在我们身边!共勉生活中的数学无处不在
希望同学们善于
用数学的视角观察世界
用数学的思维理解世界
发现生活中的数学
惊奇和趣味也许就在我们身边!共勉
斜边的平方.勾股定理的应用 学习目标
1、知识与技能
通过对一些实际问题的探究,能运用勾股定理解决一些简单的实际问题.
2、过程与方法
积极参与勾股定理的应用过程,熟练掌握其应用方法,明确应用的条件.通过练习、巩固知识、拓展知识.
3、情感、态度与价值观
培养自己的合情推理能力,体会数形结合的思维方法.提高学习热情,感受数学源于生活又服务于生活.新知探究 例1 一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,
沿着圆柱的侧面爬行到点C,试求出爬行的最
短路程. (精确到0.01cm) 新知探究4cm周长的一半答:最短路程约为10.77cm.4cm底面周长20cm变形练习 在灯罩的侧面从底部到顶部缠绕了一圈金黄色纸带作为装饰.如图灯罩的高为30cm,其底部周长为40cm,他们要剪裁纸带的长度至少为多少cm?? 一辆高2.2米,宽2米的卡车要通过一个半径为3米的半圆形隧道,它能顺利通过吗?OA1mCBD.分析:隧道宽度是足够的,所以卡车能否通过,只要看卡车位于隧道正中间时其高度是否小于( ).?
因为2.8>2.2,高度上有0.6米的余量,所以卡车能通过隧道.新知探究CD连接OD,得到RtΔOCD如何求CD呢?解:在RtΔOCD中,由勾股
定理得3m 例2 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如下图的某工厂,问这辆卡车能否通过该工厂的厂门?变形练习分析:
1、厂门的宽度足够,所以卡车能否通过,只要看卡车位于厂门正中间时,其高度是否小于( ),要求CH就必须先求( ),而要求出CD我们可以建立RtΔ( )。
2、在RtΔOCD中,直角边OD=( )
斜边OC=( )
CHCDOCD1米0.8米CH = 0.6+2.3 = 2.9>2.5 因此高度上有0.4米的余量,所以卡车能通过厂门.0.8m1m方法归纳应用勾股定理的解题思路:
从实际问题中直角三角形,运用勾股定理解决.达标反馈现准备将一块形为直角三角形的绿地扩大,使其仍为直角三角形,两直角边同时扩大到原来的两倍,问斜边扩大到原来的多少倍?解:在RtΔABC中,根据勾股定理得符合题意.2a2b所以,斜边扩大2倍符合题意.中考链接 如果将例1的圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面从点A到点B需要爬行的最短路程又是多少呢?10cm20cm拓展延伸 我家附近有棵8米高的大树,在一个雷雨天被雷电击中断裂,树的顶部落在离树根底部4米的地方,你能计算出原处的大树还有多高吗?4米ABCABC(应用勾股定理列方程)类似:教材《九章算术》
折竹抵地4米谈谈我们的收获……课堂小结我学会了……
我明白了……
我会用……
通过本节课的研究,作业:1 教材习题14.2 第1、2、3题
2 在生活中需找可以运用勾股定理解决的实际问题,并写下来予以解决.如果将例1的圆柱体换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面从点A到点B需要爬行的最短路程又是多少呢?课后思考生活中的数学无处不在
希望同学们善于
用数学的视角观察世界
用数学的思维理解世界
发现生活中的数学
惊奇和趣味也许就在我们身边!共勉生活中的数学无处不在
希望同学们善于
用数学的视角观察世界
用数学的思维理解世界
发现生活中的数学
惊奇和趣味也许就在我们身边!共勉
