与圆有关的比例线段(复习课)
图片预览


文档简介
课件11张PPT。授课教师: 陈明锋(复习课)桥亭乡桥亭中学2005年12月12日和圆有关的比例线段和圆有关的
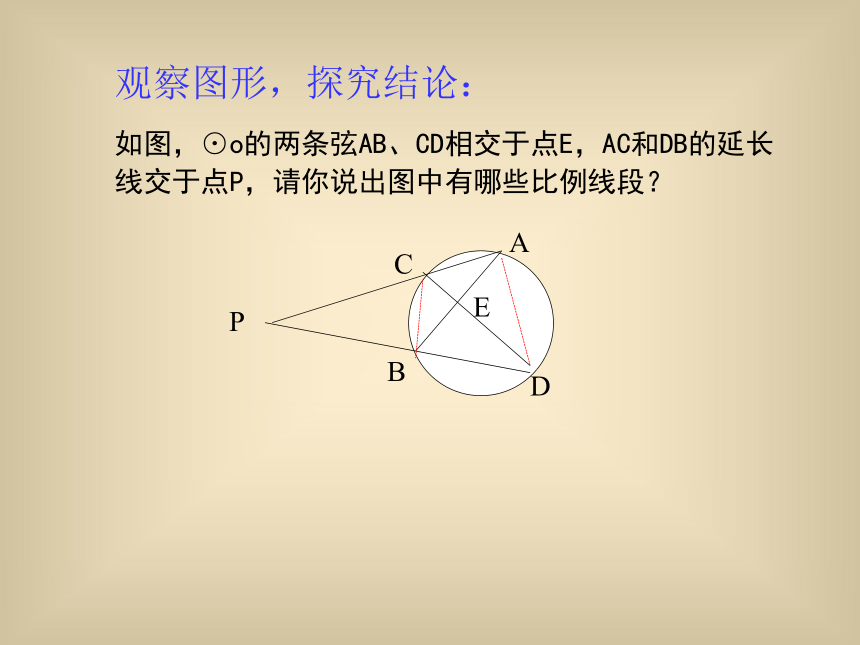
比例线段内容应用相交弦定理——推论切割线定理——推论解有关的计算和证明题作两条线段的比例中项观察图形,探究结论:
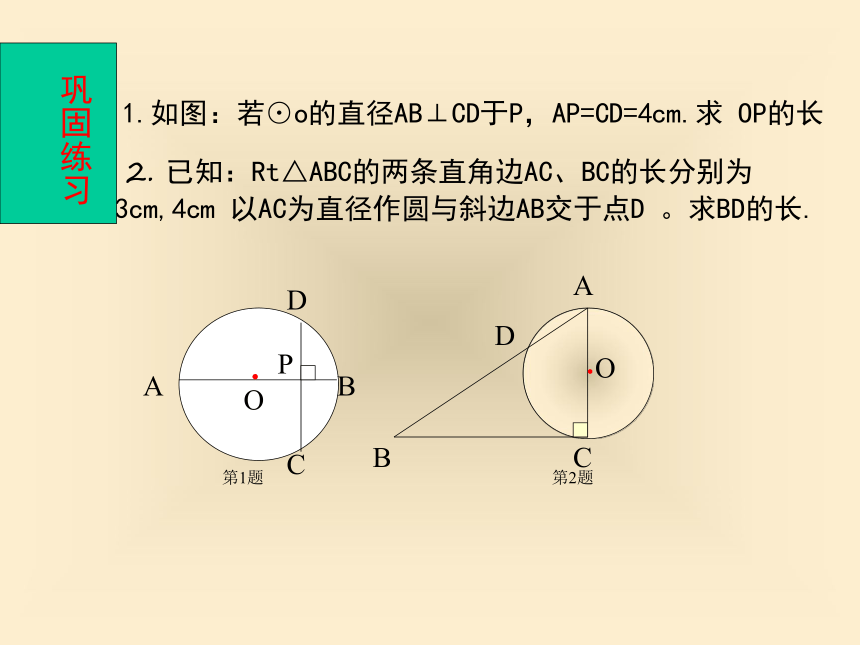
如图,⊙o的两条弦AB、CD相交于点E,AC和DB的延长 线交于点P,请你说出图中有哪些比例线段?PABCDE 2. 已知:Rt△ABC的两条直角边AC、BC的长分别为 3cm,4cm 以AC为直径作圆与斜边AB交于点D 。求BD的长.巩固练习ABCDO.ADPO.1.如图:若⊙o的直径AB⊥CD于P,AP=CD=4cm.求 OP的长C第1题第2题BACDPB3、如图,弦AB和CD交于⊙O内一点P,AP=2cm, PB=6cm
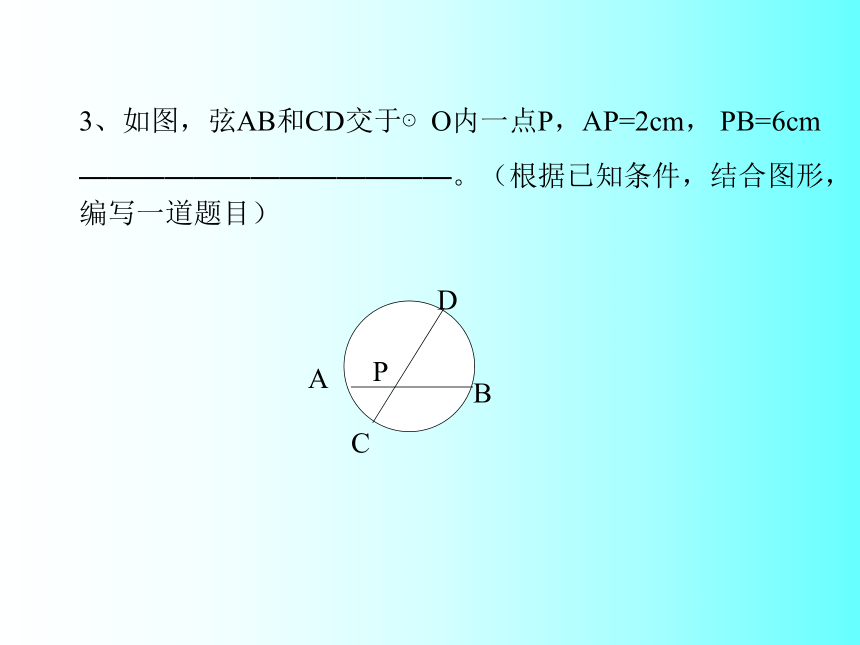
—————————————。(根据已知条件,结合图形,编写一道题目)1、已知,如图,AB是⊙O的弦,P是AB上的一点,AB=10cm,PA=4cm,OP=5cm。求⊙O的半径。 2、如图⊙O的半径为5cm,OP=8cm,若PC:CD=1:2,
求PC的长。.pABOCD第1题.pOCDABE若PC是⊙O的切线呢?POC提高练习第2题PCBAOMDN已知:如图,AB为⊙O直径,PA切⊙O于A,PCB为⊙O的割线, OM⊥BC,AM交BC于N。
求证:PN2 = PC·PB PA切⊙O于APA⊥OA ∠ PAN+∠OAM= 90° OM⊥BC ∠OMA+∠MND= 90°∠ANP=∠DNM∠PNA+∠OMA= 90°
∠OAM=∠OMA证明: PA=PN
PA2= PC.PBPN2= PC.PB已知:线段a、b(a>b)
求作:线段c,使c2=abab探索尝试多种作法一、选择题:
1.AB是⊙O的直径,弦CD⊥AB于E,
AE = 4cm,EB = 1cm ,则CD =( )
A 、2cm B、3cm C、4cm D、5 cm
2.PA为⊙O 的切线,A为切点 ,
PA = 6cm,BC = 2PB, 则PB=( )
?A、3√2 cm B、2√3cm
C、√3cm D、√2cm?
二、填空题:
1、,一条弦被分为2cm和12cm,另一条弦被分为2 :3
则两条弦长分别为____________cm.
2、从圆外一点P向圆引切线PA和割线PBC,已知割线在圆内的
部分与切线长相等,圆外部分等于2cm..则切线长为______ cm. ABCDEO.CPABCB14 和 10 达 标 检 测OGoodbye 作 业:
Ⅰ P130 2
Ⅱ 作一个正方形,使它的面积等于已知矩形的面积。谢 谢 大 家
比例线段内容应用相交弦定理——推论切割线定理——推论解有关的计算和证明题作两条线段的比例中项观察图形,探究结论:
如图,⊙o的两条弦AB、CD相交于点E,AC和DB的延长 线交于点P,请你说出图中有哪些比例线段?PABCDE 2. 已知:Rt△ABC的两条直角边AC、BC的长分别为 3cm,4cm 以AC为直径作圆与斜边AB交于点D 。求BD的长.巩固练习ABCDO.ADPO.1.如图:若⊙o的直径AB⊥CD于P,AP=CD=4cm.求 OP的长C第1题第2题BACDPB3、如图,弦AB和CD交于⊙O内一点P,AP=2cm, PB=6cm
—————————————。(根据已知条件,结合图形,编写一道题目)1、已知,如图,AB是⊙O的弦,P是AB上的一点,AB=10cm,PA=4cm,OP=5cm。求⊙O的半径。 2、如图⊙O的半径为5cm,OP=8cm,若PC:CD=1:2,
求PC的长。.pABOCD第1题.pOCDABE若PC是⊙O的切线呢?POC提高练习第2题PCBAOMDN已知:如图,AB为⊙O直径,PA切⊙O于A,PCB为⊙O的割线, OM⊥BC,AM交BC于N。
求证:PN2 = PC·PB PA切⊙O于APA⊥OA ∠ PAN+∠OAM= 90° OM⊥BC ∠OMA+∠MND= 90°∠ANP=∠DNM∠PNA+∠OMA= 90°
∠OAM=∠OMA证明: PA=PN
PA2= PC.PBPN2= PC.PB已知:线段a、b(a>b)
求作:线段c,使c2=abab探索尝试多种作法一、选择题:
1.AB是⊙O的直径,弦CD⊥AB于E,
AE = 4cm,EB = 1cm ,则CD =( )
A 、2cm B、3cm C、4cm D、5 cm
2.PA为⊙O 的切线,A为切点 ,
PA = 6cm,BC = 2PB, 则PB=( )
?A、3√2 cm B、2√3cm
C、√3cm D、√2cm?
二、填空题:
1、,一条弦被分为2cm和12cm,另一条弦被分为2 :3
则两条弦长分别为____________cm.
2、从圆外一点P向圆引切线PA和割线PBC,已知割线在圆内的
部分与切线长相等,圆外部分等于2cm..则切线长为______ cm. ABCDEO.CPABCB14 和 10 达 标 检 测OGoodbye 作 业:
Ⅰ P130 2
Ⅱ 作一个正方形,使它的面积等于已知矩形的面积。谢 谢 大 家
