湖南省株洲市第十五中学2016届九年级3月月考数学试题
文档属性
| 名称 | 湖南省株洲市第十五中学2016届九年级3月月考数学试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 170.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-28 00:00:00 | ||
图片预览


文档简介
2016年上学期九年级数学月考检测试卷
(时量:120分钟 满分:120分)
制卷人:王建明 审核人:初三数学组
一、选择题 (每小题3分, 满分30分,请将正确答案的序号填写在下表内)
题号 1 2 3 4 5 6 7 8 9 10
答案
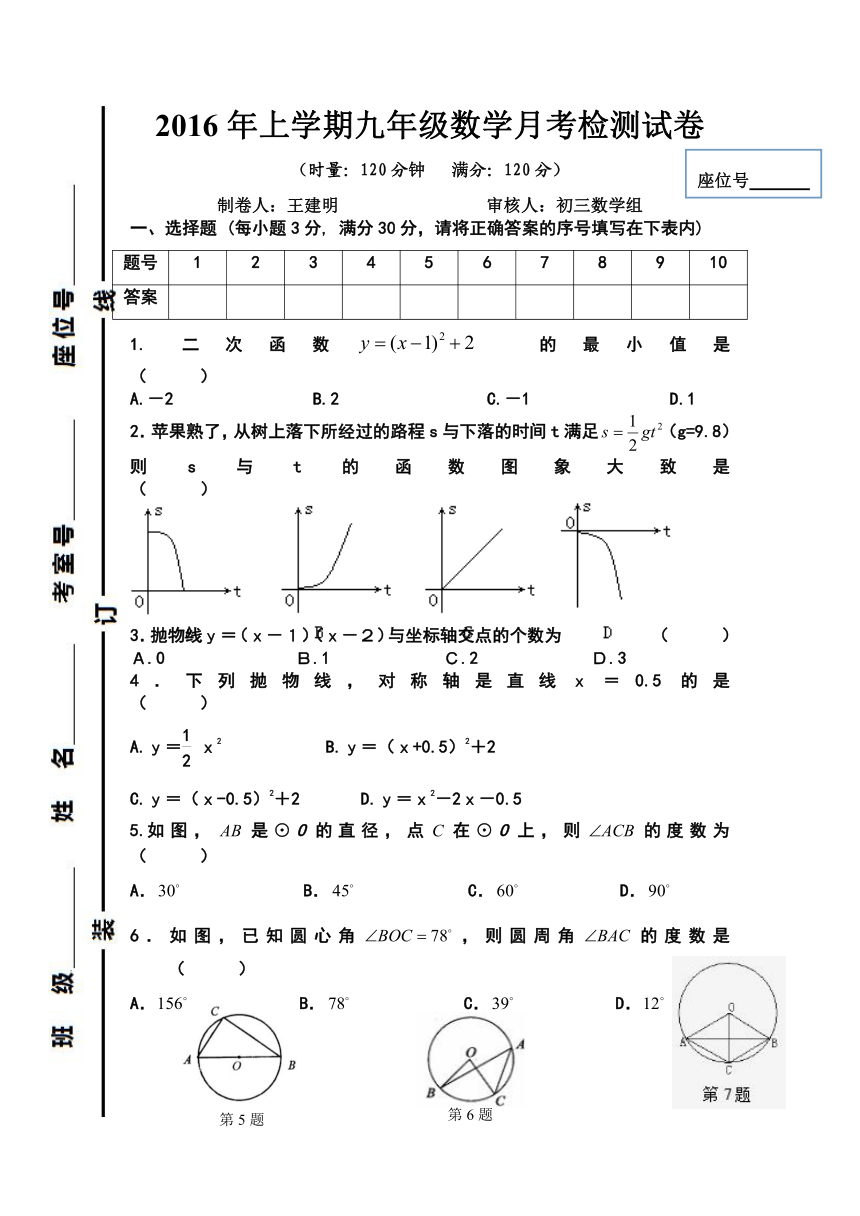
1. 二次函数 的最小值是 ( )
A.-2 B.2 C.-1 D.1
2.苹果熟了,从树上落下所经过的路程s与下落的时间t满足(g=9.8)则s与t的函数图象大致是 ( )
3.抛物线y=(x-1)(x-2)与坐标轴交点的个数为 ( )
A.0 B.1 C.2 D.3
4.下列抛物线,对称轴是直线x=0.5的 ( http: / / www.21cnjy.com )是 ( )
A.y=x2 B.y=(x+0.5)2+2
C.y=(x-0.5)2+2 D.y=x2-2x-0.5
如图,是⊙O的直径,点在⊙O上,则的度数为 ( )
A. B. C. D.
6.如图,已知圆心角,则圆周角的度数是 ( )
A. B. C. D.
7.如图所示,圆O的弦AB垂直平分半径OC.则四边形OACB是 ( )
A.正方形 B.长方形 C.菱形 D.以上答案都不对
8. 圆内接四边形ABCD中,四个角的度数比可顺次为 ( )
A. 4:3:2:1 B. 4:3:1:2 C. 4:2:3:1 D. 4:1: 3:2
9. 某几何体的三种视图如图所示,则该几何体可能是 ( )
A.圆锥体 B.球体
C.长方体 D.圆柱体
10. 如图,一个圆锥的侧面展开图是半径为10的半圆,则它的底面半径是 ( )
A.3 B.4
C.5 D.6
得分
二、填空题 (每小题3分, 满分24分)
11.抛物线 的顶点坐标是____________ .
12.将抛物线向上平移2个单位,得到抛物线的解析式是__________ .
13.抛物线根据图象可知,当x___________ 时,y随x的增大而减小.
14.圆外一点与圆上各点的距离中,最大距离为11cm,最小距离为5cm,则圆的半径为____________ .
15.已知点M到直线L的距离是3cm,若⊙M的直径10cm,则⊙M与直线L的位置关系是____________ .
16.Rt△ABC中两条直角边分别为6cm,8cm,则外接圆半径为____________ .
17.点O是ΔABC的内心,∠A=60°,则∠BOC =_______________ .
18.PA、PB分别是⊙O的切线,切点分别为A、B,∠AOB=144°,则∠P=____________.
得分
三、解答题 (满分66分)
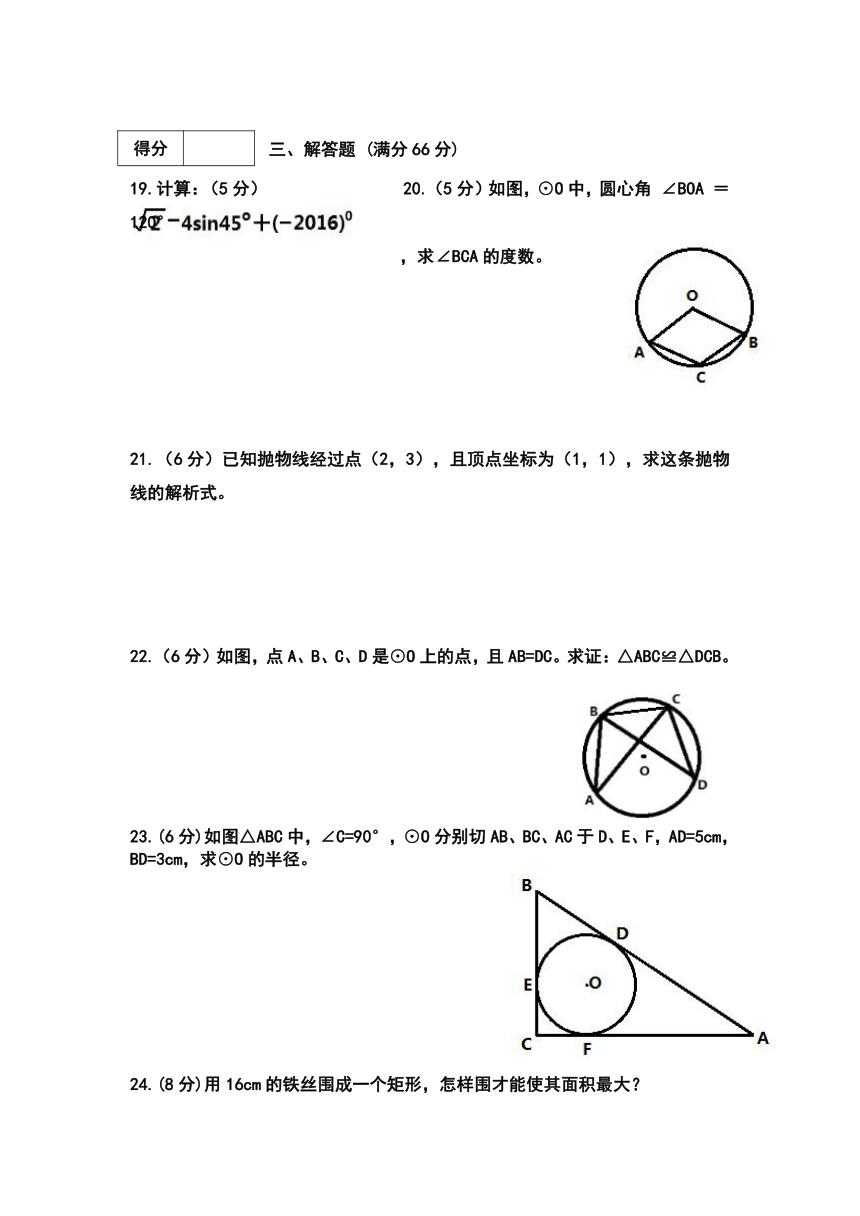
计算:(5分) 20.(5分)如图,⊙O中,圆心角 ∠BOA =120°
,求∠BCA的度数。
(6分)已知抛物线经过点(2,3),且顶点坐标为(1,1),求这条抛物线的解析式。
22.(6分)如图,点A、B、C、D是⊙O上的点,且AB=DC。求证:△ABC≌△DCB。
23.(6分)如图△ABC中,∠C=90°,⊙O分别切AB、BC、AC于D、E、F,AD=5cm,BD=3cm,求⊙O的半径。
24.(8分)用16cm的铁丝围成一个矩形,怎样围才能使其面积最大?
设矩形的一边长度为x cm,求出其面积y与x的函数关系式。
当x为多少时,矩形的面积最大?并求出矩形最大面积。
25.(8分)如图,AB是⊙O直径,EF切⊙O于C,AD⊥EF于D,求证:AC2=AD·AB。
26. (10分)如图,把两个扇形OAB与扇形OCD的圆心重合叠放在一起,且∠AOB=∠COD,连接AC.
(1)求证:△AOC≌△BOD;
(2)若OA=3cm,OC=2cm,弧AB的长为,弧CD的长为π,求阴影部分的面积.
27.(12分)如图,在平面直角坐标系中,坐标原点为O,A点坐标为(4,0),B点坐标为(﹣1,0),以AB的中点P为圆心,AB为直径作⊙P,与y轴的正半轴交于点C.
(1)求经过A、B、C三点的抛物线所对应的函数解析式;
(2)设M为(1)中抛物线的顶点,求直线MC对应的函数解析式;
(3)试说明直线MC与⊙P的位置关系,并证明你的结论.
答案:一、选择题1-5:BBCCD,6-10:CCBDC二、填空题11. (2,0) 12. y=3x2+2 13. x<1 14. 3cm 15. 相交 16. 5cm 17. 120 18. 36 0三、解答题19. 1- 20.解:∵∠BOA=120 0 ∴优弧AmB所对的圆心角的度数为240 0 ∴∠ACB=× 240 0 =120 0.解:∵顶点坐标为(1,1) 设抛物线为y = a(x-1)2 + 1 则:3 = a(2-1)2 + 1 解之:a = 2 ∴y = 2(x-1)2 + 1 = 2x2 - 4x + 3.22.证明:解:连接OE、OF. ∵AB、BC、AC为⊙O的切线 ∴∠OFC=∠OEC=∠ECF=900 , 且BD=BE=3,AD=AF=5,CE=CF ∵OE=OF ∴四边形CEOF为正方形,故EC=EO=CF=OF=r ∴BC2 + AC2 =AB2 ,即(3 + r)2 +(5 + r)2 = 82 解之: r=-4 ∵ r>0 ∴ r=-424.解:(1)一边为xcm ,则另一边为(8-x)cm.故y=x(8-x)=-x2 + 8x. (2)y=-x2 + 8x=-(x-4)2+16, 故x=4时,ymax=16。 答:(略)。证明:连接CO、CB. ∵EF为切线 ∴CO⊥EF ∵AD⊥EF ∴CO∥AD ∴∠OCA=∠DAC ∵OC=OA ∴∠OCA=∠CAO ∴∠DAC=∠CAO ∵AB为直径 ∴∠ADC=∠ACB=900 ∴△ABC∽△ACD ∴ ,即AC 2 =AD·AB 解:(1)依图有:OA=OB,OC=OD ∵∠AOB=∠COD ∴∠DOB=∠COA ∴△AOC≌△BOD(SAS) (2)S阴影=S扇形OAB-S扇形OEF =S扇形OAB-S扇形OCD=27. 解:(1)∵A(4,0),B(﹣1,0), ∴AB=5,半径是PC=PB=PA=, ∴OP=﹣1=, 在△CPO中,由勾股定理得:OC==2, ∴C(0,2), 设经过A、B、C三点抛物线解析式是y=a(x﹣4)(x+1), 把C(0,2)代入得:2=a(0﹣4)(0+1), ∴a=﹣, ∴y=﹣(x﹣4)(x+1)=﹣x2+x+2, 答:经过A、B、C三点抛物线解析式是y=﹣x2+x+2. (2)y=﹣x2+x+2=﹣+, ∴M(,), 设直线MC对应函数表达式是y=kx+b, 把C(0,2),M(,)代入得:, 解得:k=,b=2, ∴y=x+2. 答:直线MC对应函数表达式是y=x+2. (3)MC与⊙P的位置关系是相切. 证明:设直线MC交x轴于D, 当y=0时,0=x+2, ∴x=﹣,OD=, ∴D(﹣,0), 在△COD中,由勾股定理得:CD2=22+==, PC2===, PD2==, ∴CD2+PC2=PD2, ∴∠PCD=90°, ∴PC⊥DC, ∵PC为半径, ∴MC与⊙P的位置关系是相切.
座位号
第5题
第6题
(时量:120分钟 满分:120分)
制卷人:王建明 审核人:初三数学组
一、选择题 (每小题3分, 满分30分,请将正确答案的序号填写在下表内)
题号 1 2 3 4 5 6 7 8 9 10
答案
1. 二次函数 的最小值是 ( )
A.-2 B.2 C.-1 D.1
2.苹果熟了,从树上落下所经过的路程s与下落的时间t满足(g=9.8)则s与t的函数图象大致是 ( )
3.抛物线y=(x-1)(x-2)与坐标轴交点的个数为 ( )
A.0 B.1 C.2 D.3
4.下列抛物线,对称轴是直线x=0.5的 ( http: / / www.21cnjy.com )是 ( )
A.y=x2 B.y=(x+0.5)2+2
C.y=(x-0.5)2+2 D.y=x2-2x-0.5
如图,是⊙O的直径,点在⊙O上,则的度数为 ( )
A. B. C. D.
6.如图,已知圆心角,则圆周角的度数是 ( )
A. B. C. D.
7.如图所示,圆O的弦AB垂直平分半径OC.则四边形OACB是 ( )
A.正方形 B.长方形 C.菱形 D.以上答案都不对
8. 圆内接四边形ABCD中,四个角的度数比可顺次为 ( )
A. 4:3:2:1 B. 4:3:1:2 C. 4:2:3:1 D. 4:1: 3:2
9. 某几何体的三种视图如图所示,则该几何体可能是 ( )
A.圆锥体 B.球体
C.长方体 D.圆柱体
10. 如图,一个圆锥的侧面展开图是半径为10的半圆,则它的底面半径是 ( )
A.3 B.4
C.5 D.6
得分
二、填空题 (每小题3分, 满分24分)
11.抛物线 的顶点坐标是____________ .
12.将抛物线向上平移2个单位,得到抛物线的解析式是__________ .
13.抛物线根据图象可知,当x___________ 时,y随x的增大而减小.
14.圆外一点与圆上各点的距离中,最大距离为11cm,最小距离为5cm,则圆的半径为____________ .
15.已知点M到直线L的距离是3cm,若⊙M的直径10cm,则⊙M与直线L的位置关系是____________ .
16.Rt△ABC中两条直角边分别为6cm,8cm,则外接圆半径为____________ .
17.点O是ΔABC的内心,∠A=60°,则∠BOC =_______________ .
18.PA、PB分别是⊙O的切线,切点分别为A、B,∠AOB=144°,则∠P=____________.
得分
三、解答题 (满分66分)
计算:(5分) 20.(5分)如图,⊙O中,圆心角 ∠BOA =120°
,求∠BCA的度数。
(6分)已知抛物线经过点(2,3),且顶点坐标为(1,1),求这条抛物线的解析式。
22.(6分)如图,点A、B、C、D是⊙O上的点,且AB=DC。求证:△ABC≌△DCB。
23.(6分)如图△ABC中,∠C=90°,⊙O分别切AB、BC、AC于D、E、F,AD=5cm,BD=3cm,求⊙O的半径。
24.(8分)用16cm的铁丝围成一个矩形,怎样围才能使其面积最大?
设矩形的一边长度为x cm,求出其面积y与x的函数关系式。
当x为多少时,矩形的面积最大?并求出矩形最大面积。
25.(8分)如图,AB是⊙O直径,EF切⊙O于C,AD⊥EF于D,求证:AC2=AD·AB。
26. (10分)如图,把两个扇形OAB与扇形OCD的圆心重合叠放在一起,且∠AOB=∠COD,连接AC.
(1)求证:△AOC≌△BOD;
(2)若OA=3cm,OC=2cm,弧AB的长为,弧CD的长为π,求阴影部分的面积.
27.(12分)如图,在平面直角坐标系中,坐标原点为O,A点坐标为(4,0),B点坐标为(﹣1,0),以AB的中点P为圆心,AB为直径作⊙P,与y轴的正半轴交于点C.
(1)求经过A、B、C三点的抛物线所对应的函数解析式;
(2)设M为(1)中抛物线的顶点,求直线MC对应的函数解析式;
(3)试说明直线MC与⊙P的位置关系,并证明你的结论.
答案:一、选择题1-5:BBCCD,6-10:CCBDC二、填空题11. (2,0) 12. y=3x2+2 13. x<1 14. 3cm 15. 相交 16. 5cm 17. 120 18. 36 0三、解答题19. 1- 20.解:∵∠BOA=120 0 ∴优弧AmB所对的圆心角的度数为240 0 ∴∠ACB=× 240 0 =120 0.解:∵顶点坐标为(1,1) 设抛物线为y = a(x-1)2 + 1 则:3 = a(2-1)2 + 1 解之:a = 2 ∴y = 2(x-1)2 + 1 = 2x2 - 4x + 3.22.证明:解:连接OE、OF. ∵AB、BC、AC为⊙O的切线 ∴∠OFC=∠OEC=∠ECF=900 , 且BD=BE=3,AD=AF=5,CE=CF ∵OE=OF ∴四边形CEOF为正方形,故EC=EO=CF=OF=r ∴BC2 + AC2 =AB2 ,即(3 + r)2 +(5 + r)2 = 82 解之: r=-4 ∵ r>0 ∴ r=-424.解:(1)一边为xcm ,则另一边为(8-x)cm.故y=x(8-x)=-x2 + 8x. (2)y=-x2 + 8x=-(x-4)2+16, 故x=4时,ymax=16。 答:(略)。证明:连接CO、CB. ∵EF为切线 ∴CO⊥EF ∵AD⊥EF ∴CO∥AD ∴∠OCA=∠DAC ∵OC=OA ∴∠OCA=∠CAO ∴∠DAC=∠CAO ∵AB为直径 ∴∠ADC=∠ACB=900 ∴△ABC∽△ACD ∴ ,即AC 2 =AD·AB 解:(1)依图有:OA=OB,OC=OD ∵∠AOB=∠COD ∴∠DOB=∠COA ∴△AOC≌△BOD(SAS) (2)S阴影=S扇形OAB-S扇形OEF =S扇形OAB-S扇形OCD=27. 解:(1)∵A(4,0),B(﹣1,0), ∴AB=5,半径是PC=PB=PA=, ∴OP=﹣1=, 在△CPO中,由勾股定理得:OC==2, ∴C(0,2), 设经过A、B、C三点抛物线解析式是y=a(x﹣4)(x+1), 把C(0,2)代入得:2=a(0﹣4)(0+1), ∴a=﹣, ∴y=﹣(x﹣4)(x+1)=﹣x2+x+2, 答:经过A、B、C三点抛物线解析式是y=﹣x2+x+2. (2)y=﹣x2+x+2=﹣+, ∴M(,), 设直线MC对应函数表达式是y=kx+b, 把C(0,2),M(,)代入得:, 解得:k=,b=2, ∴y=x+2. 答:直线MC对应函数表达式是y=x+2. (3)MC与⊙P的位置关系是相切. 证明:设直线MC交x轴于D, 当y=0时,0=x+2, ∴x=﹣,OD=, ∴D(﹣,0), 在△COD中,由勾股定理得:CD2=22+==, PC2===, PD2==, ∴CD2+PC2=PD2, ∴∠PCD=90°, ∴PC⊥DC, ∵PC为半径, ∴MC与⊙P的位置关系是相切.
座位号
第5题
第6题
同课章节目录
