2024-2025学年第一学期甘肃省武威第二十七中学九年级数学人教版第二十二章《二次函数》练习卷(含答案)
文档属性
| 名称 | 2024-2025学年第一学期甘肃省武威第二十七中学九年级数学人教版第二十二章《二次函数》练习卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 698.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-04 00:00:00 | ||
图片预览




文档简介
2024-2025学年第一学期甘肃省武威市九年级
数学人教版第二十二章《二次函数》练习卷
一、单选题
1.下列函数中,是二次函数的是( )
A. B.
C. D.
2.已知是关于x的二次函数,则a的取值范围是( )
A. B. C. D.
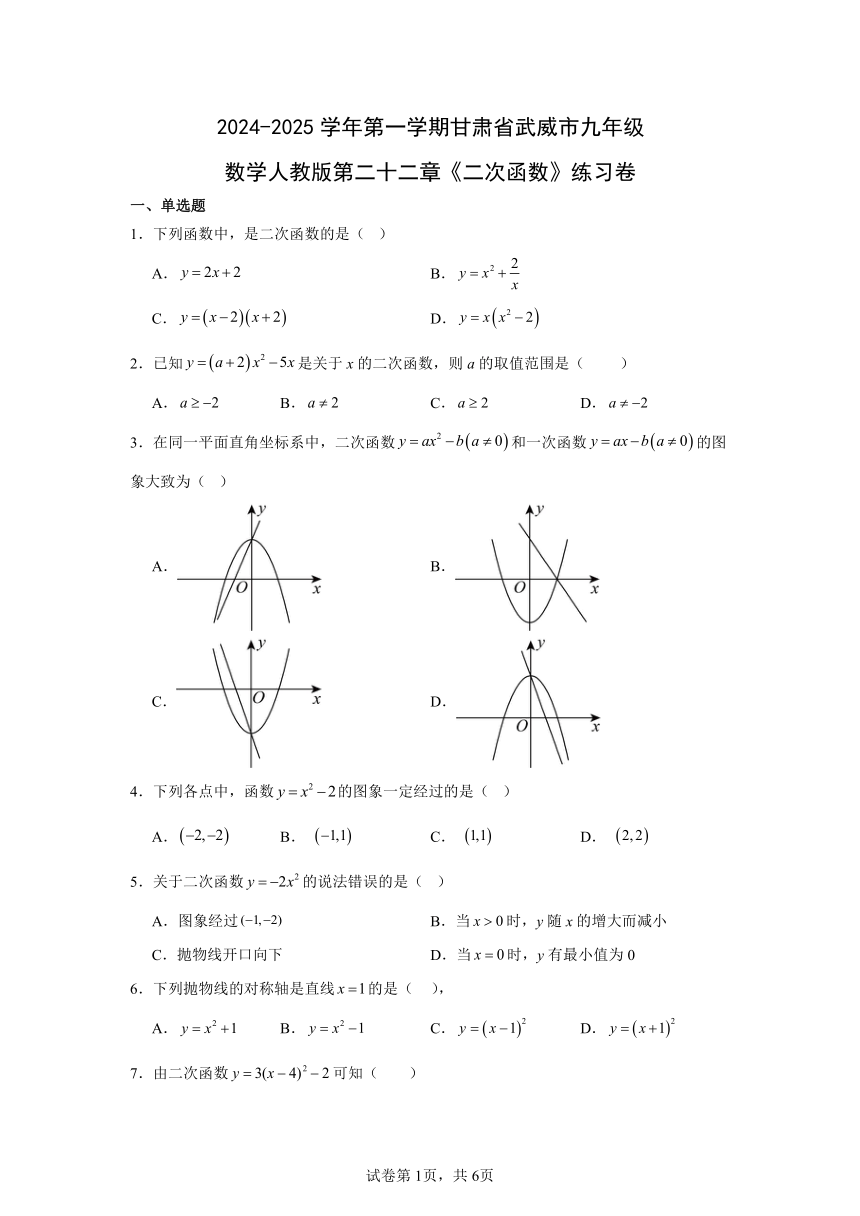
3.在同一平面直角坐标系中,二次函数和一次函数的图象大致为( )
A. B.
C. D.
4.下列各点中,函数的图象一定经过的是( )
A. B. C. D.
5.关于二次函数的说法错误的是( )
A.图象经过 B.当时,y随x的增大而减小
C.抛物线开口向下 D.当时,y有最小值为0
6.下列抛物线的对称轴是直线的是( ),
A. B. C. D.
7.由二次函数可知( )
A.其图象的开口向下
B.其图象的对称轴为直线
C.其最小值为2
D.当时,y随x的增大而减小
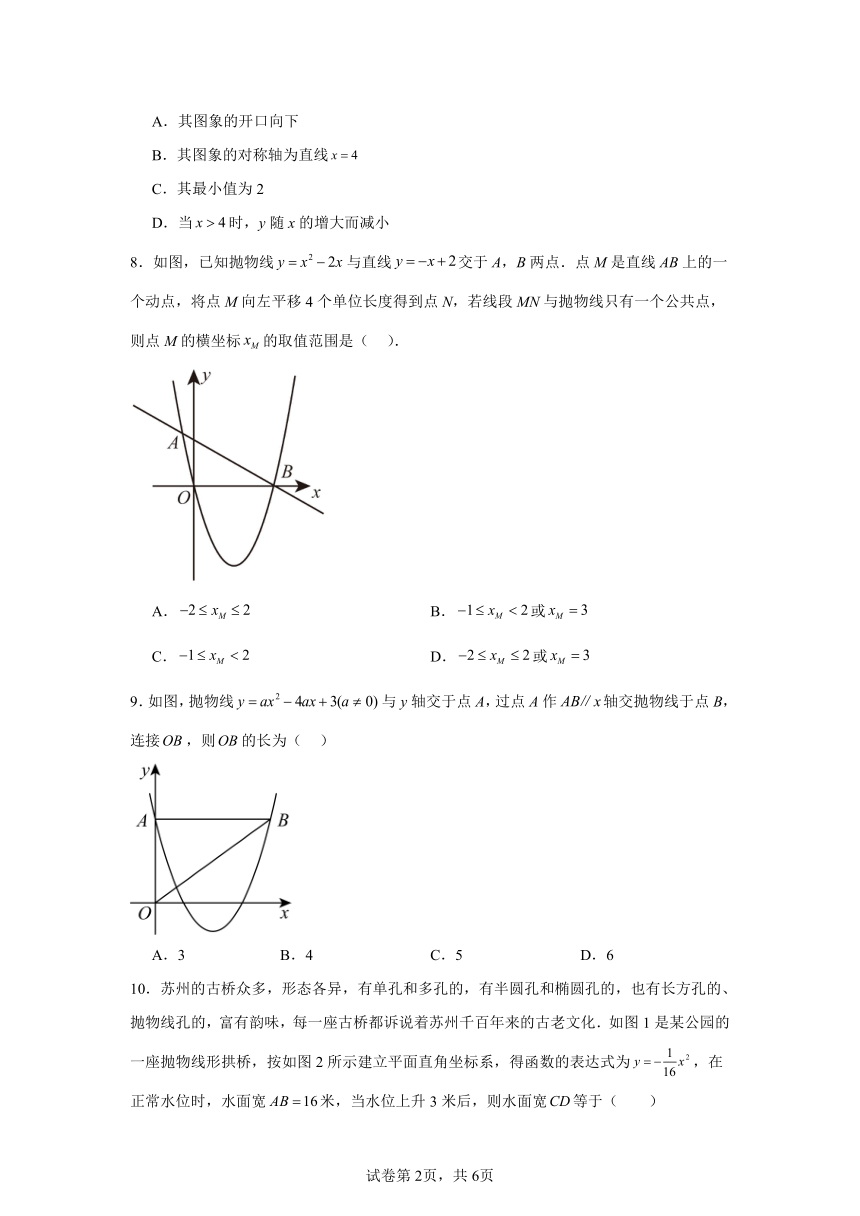
8.如图,已知抛物线与直线交于A,B两点.点M是直线AB上的一个动点,将点M向左平移4个单位长度得到点N,若线段MN与抛物线只有一个公共点,则点M的横坐标的取值范围是( ).
A. B.或
C. D.或
9.如图,抛物线与y轴交于点A,过点A作轴交抛物线于点B,连接,则的长为( )
A.3 B.4 C.5 D.6
10.苏州的古桥众多,形态各异,有单孔和多孔的,有半圆孔和椭圆孔的,也有长方孔的、抛物线孔的,富有韵味,每一座古桥都诉说着苏州千百年来的古老文化.如图1是某公园的一座抛物线形拱桥,按如图2所示建立平面直角坐标系,得函数的表达式为,在正常水位时,水面宽米,当水位上升3米后,则水面宽等于( )
A.4米 B.8米 C.米 D.米
二、填空题
11.关于二次函数,当时,的取值范围是 .
12.若关于x的函数是二次函数,且其有最大值,则 .
13.已知抛物线过,,三点,则,,的大小关系是 .(用“”号连接)
14.已知抛物线,当时,函数的最大值是6,最小值是2,则的取值范围是 .
15.已知二次函数图象上有两个不同点、,则 .
16.已知拋物线经过点,那么点A关于对称轴对称的点B坐标为 .
17.若时,函数的最大值为17,则 .
18.如图,已知二次函数的图象与x轴交于A,B两点,与y轴交于点C,P点为该图象在第一象限内的一点,过点P作直线的平行线,交x轴于点M.若点P从点C出发,沿着抛物线运动到点B,则点M经过的路程为 .
三、解答题
19.已知二次函数.
(1)该函数图象的开口向__________,顶点坐标为__________,对称轴为直线__________,函数图象与轴的交点坐标为__________,与轴的交点坐标为__________.
(2)在如图所示的坐标系中画出该二次函数的图象.
(3)根据图象判断,当时,的取值范围是__________.
(4)若点与是此二次函数图象上两点,则__________.(填“>”“<”或“=”)
20.已知是关于的二次函数,求的值.
21.若二次函数的图象经过点,求该函数的解析式并写出对称轴.
22.已知是关于的二次函数.
(1)求值;
(2)若,直接写出的取值范围.
23.抛物线与直线的一个交点为,
(1)求和.
(2)求另一个交点的坐标.
24.如图,点A、B分别在二次函数的图象上,且线段轴,若.
(1)求点A、B的坐标.
(2)求三角形的面积.
25.某水果店购入一批进价为10元/千克的水果进行销售,经调查发现:销售单价不低于进价且不超过30元/千克时,日销售量(千克)与销售单价(元)是一次函数关系,如下表.
销售单价 20 22 24
销售量 32 28 24
(1)求与的函数表达式.
(2)当销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若为了尽快销售完这批水果,水果店决定降价销售,每千克降价元,该店经调查发现当取值在一定范围内时,销售利润会随着售价的增加而增加,求的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D D D C B B C B
11.
12.
13.
14.
15.0
16.
17.
18.
19.(1)解:∵,,
∴抛物线开口向下,顶点坐标为,对称轴为直线,
令,即,
解得或,
故函数图象与轴的交点坐标为,,
令,则,
故与轴的交点坐标为;
故答案为:向下,,,,,;
(2)解:根据抛物线与坐标轴的交点和顶点坐标,描点作出函数图象:
(3)解:根据图象,当时,的取值范围是,
故答案为:.
(4)解:∵点在轴下方,而在轴上方,
∴.
故答案为:<.
20.解:依题意,
解得:
又
∴
21.解:根据题意,得,解得,
∴所求的函数解析式为,
∴对称轴是y轴.
22.(1)解:根据题意得:,且,
解方程得:或(舍去),
∴;
(2)解:∵,
∴抛物线开口向上,且对称轴为:
∵时,解方程得,,,
∴当时,.
23.(1)解:把代入可得:
,
∴交点坐标为:;
把代入可得:
,
解得:;
(2)由(1)得:,
∴,
∴,
解得:,,
∴或,
∴函数的另一个交点坐标为:.
24.(1)
轴,,
点的横坐标为,
,
点的坐标为,
点、关于轴对称,
点.
(2)
点,点.
,
25.(1)解:设,由题意得,
,
解得:,
∴y与x的函数表达式为,
答:y与x的函数表达式为;
(2)解:设日销售利润为w元,由题意得,
,
∵销售单价不低于进价且不超过30元/千克,
∴,
∴当时,w有最大值338元,
答:当销售单价定为23元时,所获日销售利润最大,最大利润是338元;
(3)解:由题意得,
∴对称轴为直线,
∴当时销售利润会随着售价的增加而增加,
∵销售单价不低于进价且不超过30元/千克,
∴,
∵该店经调查发现当取值在一定范围内时,销售利润会随着售价的增加而增加,
∴当时销售利润会随着售价的增加而增加,
解得,
∵,
∴.
答案第1页,共2页
答案第1页,共2页
数学人教版第二十二章《二次函数》练习卷
一、单选题
1.下列函数中,是二次函数的是( )
A. B.
C. D.
2.已知是关于x的二次函数,则a的取值范围是( )
A. B. C. D.
3.在同一平面直角坐标系中,二次函数和一次函数的图象大致为( )
A. B.
C. D.
4.下列各点中,函数的图象一定经过的是( )
A. B. C. D.
5.关于二次函数的说法错误的是( )
A.图象经过 B.当时,y随x的增大而减小
C.抛物线开口向下 D.当时,y有最小值为0
6.下列抛物线的对称轴是直线的是( ),
A. B. C. D.
7.由二次函数可知( )
A.其图象的开口向下
B.其图象的对称轴为直线
C.其最小值为2
D.当时,y随x的增大而减小
8.如图,已知抛物线与直线交于A,B两点.点M是直线AB上的一个动点,将点M向左平移4个单位长度得到点N,若线段MN与抛物线只有一个公共点,则点M的横坐标的取值范围是( ).
A. B.或
C. D.或
9.如图,抛物线与y轴交于点A,过点A作轴交抛物线于点B,连接,则的长为( )
A.3 B.4 C.5 D.6
10.苏州的古桥众多,形态各异,有单孔和多孔的,有半圆孔和椭圆孔的,也有长方孔的、抛物线孔的,富有韵味,每一座古桥都诉说着苏州千百年来的古老文化.如图1是某公园的一座抛物线形拱桥,按如图2所示建立平面直角坐标系,得函数的表达式为,在正常水位时,水面宽米,当水位上升3米后,则水面宽等于( )
A.4米 B.8米 C.米 D.米
二、填空题
11.关于二次函数,当时,的取值范围是 .
12.若关于x的函数是二次函数,且其有最大值,则 .
13.已知抛物线过,,三点,则,,的大小关系是 .(用“”号连接)
14.已知抛物线,当时,函数的最大值是6,最小值是2,则的取值范围是 .
15.已知二次函数图象上有两个不同点、,则 .
16.已知拋物线经过点,那么点A关于对称轴对称的点B坐标为 .
17.若时,函数的最大值为17,则 .
18.如图,已知二次函数的图象与x轴交于A,B两点,与y轴交于点C,P点为该图象在第一象限内的一点,过点P作直线的平行线,交x轴于点M.若点P从点C出发,沿着抛物线运动到点B,则点M经过的路程为 .
三、解答题
19.已知二次函数.
(1)该函数图象的开口向__________,顶点坐标为__________,对称轴为直线__________,函数图象与轴的交点坐标为__________,与轴的交点坐标为__________.
(2)在如图所示的坐标系中画出该二次函数的图象.
(3)根据图象判断,当时,的取值范围是__________.
(4)若点与是此二次函数图象上两点,则__________.(填“>”“<”或“=”)
20.已知是关于的二次函数,求的值.
21.若二次函数的图象经过点,求该函数的解析式并写出对称轴.
22.已知是关于的二次函数.
(1)求值;
(2)若,直接写出的取值范围.
23.抛物线与直线的一个交点为,
(1)求和.
(2)求另一个交点的坐标.
24.如图,点A、B分别在二次函数的图象上,且线段轴,若.
(1)求点A、B的坐标.
(2)求三角形的面积.
25.某水果店购入一批进价为10元/千克的水果进行销售,经调查发现:销售单价不低于进价且不超过30元/千克时,日销售量(千克)与销售单价(元)是一次函数关系,如下表.
销售单价 20 22 24
销售量 32 28 24
(1)求与的函数表达式.
(2)当销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若为了尽快销售完这批水果,水果店决定降价销售,每千克降价元,该店经调查发现当取值在一定范围内时,销售利润会随着售价的增加而增加,求的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D D D C B B C B
11.
12.
13.
14.
15.0
16.
17.
18.
19.(1)解:∵,,
∴抛物线开口向下,顶点坐标为,对称轴为直线,
令,即,
解得或,
故函数图象与轴的交点坐标为,,
令,则,
故与轴的交点坐标为;
故答案为:向下,,,,,;
(2)解:根据抛物线与坐标轴的交点和顶点坐标,描点作出函数图象:
(3)解:根据图象,当时,的取值范围是,
故答案为:.
(4)解:∵点在轴下方,而在轴上方,
∴.
故答案为:<.
20.解:依题意,
解得:
又
∴
21.解:根据题意,得,解得,
∴所求的函数解析式为,
∴对称轴是y轴.
22.(1)解:根据题意得:,且,
解方程得:或(舍去),
∴;
(2)解:∵,
∴抛物线开口向上,且对称轴为:
∵时,解方程得,,,
∴当时,.
23.(1)解:把代入可得:
,
∴交点坐标为:;
把代入可得:
,
解得:;
(2)由(1)得:,
∴,
∴,
解得:,,
∴或,
∴函数的另一个交点坐标为:.
24.(1)
轴,,
点的横坐标为,
,
点的坐标为,
点、关于轴对称,
点.
(2)
点,点.
,
25.(1)解:设,由题意得,
,
解得:,
∴y与x的函数表达式为,
答:y与x的函数表达式为;
(2)解:设日销售利润为w元,由题意得,
,
∵销售单价不低于进价且不超过30元/千克,
∴,
∴当时,w有最大值338元,
答:当销售单价定为23元时,所获日销售利润最大,最大利润是338元;
(3)解:由题意得,
∴对称轴为直线,
∴当时销售利润会随着售价的增加而增加,
∵销售单价不低于进价且不超过30元/千克,
∴,
∵该店经调查发现当取值在一定范围内时,销售利润会随着售价的增加而增加,
∴当时销售利润会随着售价的增加而增加,
解得,
∵,
∴.
答案第1页,共2页
答案第1页,共2页
同课章节目录
