7.2正弦,余弦 同步练习(含答案)
文档属性
| 名称 | 7.2正弦,余弦 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 172.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
7.2正弦,余弦
一、填空题
1.如图,△ABC的顶点都在方格纸的格点上,则cosA=
2.如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=6,则AC= .
3.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b,c,a=3,c=5,则tanB= .
4.如图是某商场营业大厅自动扶梯的示意图,自动扶梯AB的倾斜角为37°,大厅两层之间的距离BC为6m,则自动扶梯AB的长约为 m(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
5.在 Rt△ABC中, , ,则 .
6.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,下列式子:①a=c sinB,②a=c cosB,③a=c tanB,④a= ,必定成立的是 .
二、单选题
7.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,则( )
A. B. C. D.
8.在Rt△ABC中,∠C=90°,AB=6,AC=4,则cosA的值是( )
A. B. C. D.
9.如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值为( )
A. B. C. D.
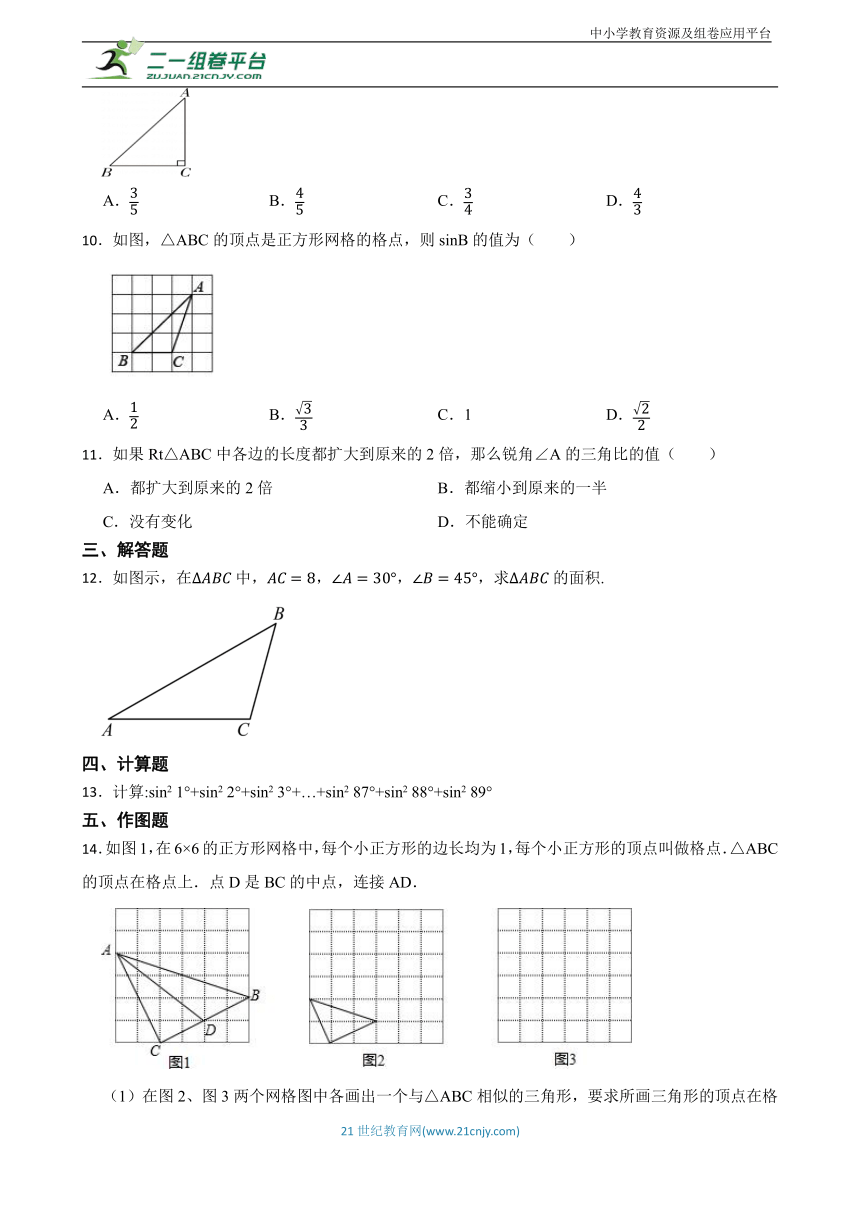
10.如图,△ABC的顶点是正方形网格的格点,则sinB的值为( )
A. B. C.1 D.
11.如果Rt△ABC中各边的长度都扩大到原来的2倍,那么锐角∠A的三角比的值( )
A.都扩大到原来的2倍 B.都缩小到原来的一半
C.没有变化 D.不能确定
三、解答题
12.如图示,在中,,,,求的面积.
四、计算题
13.计算:sin2 1°+sin2 2°+sin2 3°+…+sin2 87°+sin2 88°+sin2 89°
五、作图题
14.如图1,在6×6的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.△ABC的顶点在格点上.点D是BC的中点,连接AD.
(1)在图2、图3两个网格图中各画出一个与△ABC相似的三角形,要求所画三角形的顶点在格点上,相似比各不相同,且与△ABC的相似比不为1;
(2)tan∠CAD= .
六、综合题
15.如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα= = ,根据上述角的余切定义,解下列问题:
(1)ctan30°= ;
(2)如图,已知tanA= ,其中∠A为锐角,试求ctanA的值.
16.如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)由AB,BD, 围成的曲边三角形的面积是 ;
(2)求证:DE是⊙O的切线;
(3)求线段DE的长.
17.已知在△ABC中,∠C=90°,AB=4,AC=.
(1)求BC;
(2)求sinA.
答案解析部分
1.【答案】
【知识点】锐角三角函数的定义
2.【答案】
【知识点】圆周角定理;锐角三角函数的定义
3.【答案】
【知识点】锐角三角函数的定义
4.【答案】10
【知识点】锐角三角函数的定义
5.【答案】
【知识点】锐角三角函数的定义
6.【答案】②
【知识点】锐角三角函数的定义
7.【答案】C
【知识点】锐角三角函数的定义
8.【答案】B
【知识点】锐角三角函数的定义
9.【答案】A
【知识点】锐角三角函数的定义
10.【答案】D
【知识点】勾股定理;锐角三角函数的定义
11.【答案】C
【知识点】锐角三角函数的定义
12.【答案】
【知识点】锐角三角函数的定义
13.【答案】解:原式=sin21°+sin22°+…+sin245°+cos244°+cos243°+…+cos22°+cos21°
=(sin21°+sin289°)+(sin22°+sin288°)+…+(sin244°+sin246°)+sin245°
=1+1+…+1+
=44+0.5
=44.5 .
【知识点】互余两角三角函数的关系
14.【答案】(1)解:如图所示:△EMF和△A′B′C′即为所求;
(2)
【知识点】勾股定理;相似三角形的性质;锐角三角函数的定义
15.【答案】(1)
(2)解:∵tanA= ,
∴设BC=3,AC=4,
∴ctanA= =
【知识点】锐角三角函数的定义
16.【答案】(1)
(2)证明:由(1)知∠AOD=90°,即OD⊥AB.
∵DE∥AB,∴OD⊥DE,
∴DE是⊙O的切线;
(3)解:∵AB=10、AC=6,∴BC= =8. 过点A作AF⊥DE于点F,
则四边形AODF是正方形,∴AF=OD=FD=5,∴∠EAF=90°﹣∠CAB=∠ABC,
∴tan∠EAF=tan∠CBA,
∴ ,即 , ∴EF= ,
∴DE=DF+EF= +5= .
【知识点】勾股定理;切线的判定;锐角三角函数的定义
17.【答案】(1)解:在△ABC中,∠C=90°,AB=4,AC=.
(2)解:sinA=
【知识点】勾股定理;锐角三角函数的定义
21世纪教育网(www.21cnjy.com)
7.2正弦,余弦
一、填空题
1.如图,△ABC的顶点都在方格纸的格点上,则cosA=
2.如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=6,则AC= .
3.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b,c,a=3,c=5,则tanB= .
4.如图是某商场营业大厅自动扶梯的示意图,自动扶梯AB的倾斜角为37°,大厅两层之间的距离BC为6m,则自动扶梯AB的长约为 m(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
5.在 Rt△ABC中, , ,则 .
6.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,下列式子:①a=c sinB,②a=c cosB,③a=c tanB,④a= ,必定成立的是 .
二、单选题
7.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,则( )
A. B. C. D.
8.在Rt△ABC中,∠C=90°,AB=6,AC=4,则cosA的值是( )
A. B. C. D.
9.如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值为( )
A. B. C. D.
10.如图,△ABC的顶点是正方形网格的格点,则sinB的值为( )
A. B. C.1 D.
11.如果Rt△ABC中各边的长度都扩大到原来的2倍,那么锐角∠A的三角比的值( )
A.都扩大到原来的2倍 B.都缩小到原来的一半
C.没有变化 D.不能确定
三、解答题
12.如图示,在中,,,,求的面积.
四、计算题
13.计算:sin2 1°+sin2 2°+sin2 3°+…+sin2 87°+sin2 88°+sin2 89°
五、作图题
14.如图1,在6×6的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.△ABC的顶点在格点上.点D是BC的中点,连接AD.
(1)在图2、图3两个网格图中各画出一个与△ABC相似的三角形,要求所画三角形的顶点在格点上,相似比各不相同,且与△ABC的相似比不为1;
(2)tan∠CAD= .
六、综合题
15.如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα= = ,根据上述角的余切定义,解下列问题:
(1)ctan30°= ;
(2)如图,已知tanA= ,其中∠A为锐角,试求ctanA的值.
16.如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)由AB,BD, 围成的曲边三角形的面积是 ;
(2)求证:DE是⊙O的切线;
(3)求线段DE的长.
17.已知在△ABC中,∠C=90°,AB=4,AC=.
(1)求BC;
(2)求sinA.
答案解析部分
1.【答案】
【知识点】锐角三角函数的定义
2.【答案】
【知识点】圆周角定理;锐角三角函数的定义
3.【答案】
【知识点】锐角三角函数的定义
4.【答案】10
【知识点】锐角三角函数的定义
5.【答案】
【知识点】锐角三角函数的定义
6.【答案】②
【知识点】锐角三角函数的定义
7.【答案】C
【知识点】锐角三角函数的定义
8.【答案】B
【知识点】锐角三角函数的定义
9.【答案】A
【知识点】锐角三角函数的定义
10.【答案】D
【知识点】勾股定理;锐角三角函数的定义
11.【答案】C
【知识点】锐角三角函数的定义
12.【答案】
【知识点】锐角三角函数的定义
13.【答案】解:原式=sin21°+sin22°+…+sin245°+cos244°+cos243°+…+cos22°+cos21°
=(sin21°+sin289°)+(sin22°+sin288°)+…+(sin244°+sin246°)+sin245°
=1+1+…+1+
=44+0.5
=44.5 .
【知识点】互余两角三角函数的关系
14.【答案】(1)解:如图所示:△EMF和△A′B′C′即为所求;
(2)
【知识点】勾股定理;相似三角形的性质;锐角三角函数的定义
15.【答案】(1)
(2)解:∵tanA= ,
∴设BC=3,AC=4,
∴ctanA= =
【知识点】锐角三角函数的定义
16.【答案】(1)
(2)证明:由(1)知∠AOD=90°,即OD⊥AB.
∵DE∥AB,∴OD⊥DE,
∴DE是⊙O的切线;
(3)解:∵AB=10、AC=6,∴BC= =8. 过点A作AF⊥DE于点F,
则四边形AODF是正方形,∴AF=OD=FD=5,∴∠EAF=90°﹣∠CAB=∠ABC,
∴tan∠EAF=tan∠CBA,
∴ ,即 , ∴EF= ,
∴DE=DF+EF= +5= .
【知识点】勾股定理;切线的判定;锐角三角函数的定义
17.【答案】(1)解:在△ABC中,∠C=90°,AB=4,AC=.
(2)解:sinA=
【知识点】勾股定理;锐角三角函数的定义
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
