2.1 简谐运动 (共20张PPT) 课件 2024-2025学年高二物理粤教版(2019)选择性必修第一册
文档属性
| 名称 | 2.1 简谐运动 (共20张PPT) 课件 2024-2025学年高二物理粤教版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 15.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-03 14:47:07 | ||
图片预览







文档简介
(共20张PPT)
第二章 机械振动
第1节 简谐运动
波动过后的琴弦
摩天大楼和琴弦都在来回的振动。
思考:这些运动他们都有些什么共同的特征?
物体在某个固定位置附近做重复的往返运动.
观察现象
1、了解机械振动和简谐运动的基础知识。
2、正确理解简谐运动x-t图象的物理意义,并学会分析简谐运动的图像。
3、理解简谐运动的能量特征
一、认识机械振动和简谐运动
1.机械振动
定义:物体(或物体的一部分)在一个位置附近做的往复运动称为机械振动,简称振动。
2.特征:
(1)中心位置(平衡位置)
(2)往复运动
振动物体静止时的位置
“对称性”
“周期性”
定义:
物体在与平衡位置的位移大小成正比,并且总指向平衡位置的回复力的作用下的振动,叫作简谐振动.
振子的位移-时间函数为正弦或者余弦函数,具有这种特征的运动叫作简谐运动.
简谐运动是最简单、最基本的振动
(2)动力学角度
(1)运动学角度
3.简谐运动
为什么弹簧和滑块的振动越来越弱?
把一个滑块装在弹簧的一端,弹簧的另一端固定,滑块在杆上能够自由滑动。把滑块拉向一侧,然后放开,它就左右运动起来。
①阻力(空气阻力、摩擦力…)
②弹簧本身的质量
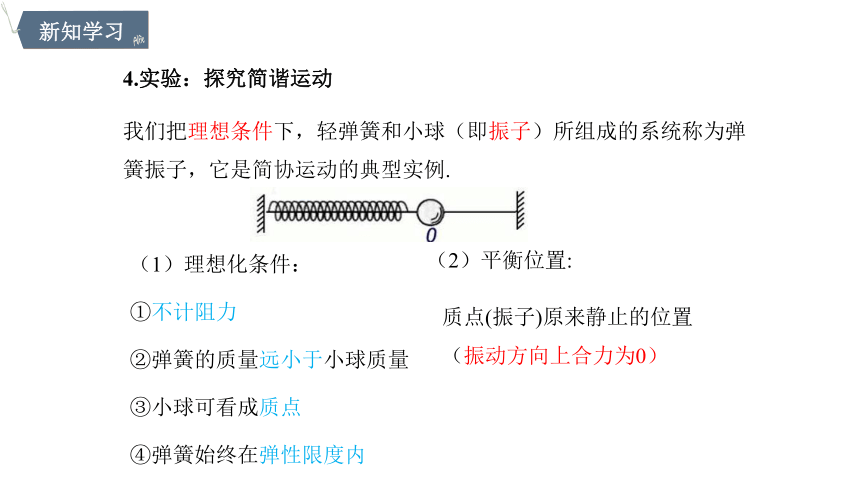
4.实验:探究简谐运动
(1)理想化条件:
①不计阻力
②弹簧的质量远小于小球质量
③小球可看成质点
④弹簧始终在弹性限度内
我们把理想条件下,轻弹簧和小球(即振子)所组成的系统称为弹簧振子,它是简协运动的典型实例.
(2)平衡位置:
质点(振子)原来静止的位置
(振动方向上合力为0)
4.实验:探究简谐运动
振子在振动过程中的受力情况如何 力与位移关系是什么?
对弹簧振子进行受力分析,弹簧振子在振动过程中,所受的重力和支持力平衡,对振子的运动无影响.
影响振子运动的只有弹簧的弹力.
(3)振子在振动过程中的受力情况:
这个力的方向跟振子偏离平衡位置的位移方向相反,总指向平衡位置,它的作用是使振子能返回平衡位置,这个力叫作回复力.
FN
G
4.实验:探究简谐运动
F=-kx
振子所受回复力的大小跟振子偏离平衡位移的位移x的大小成正比。
实验结论:弹簧振子是在跟平衡位置的位移大小成正比并且总指向平衡位置的回复力的作用下的振动,从动力学上验证了简谐振动。
负号表示回复力的方向跟振子偏离平衡位置的位移方向相反。
即:
4.实验:探究简谐运动
5.弹簧振子的位移随时间变化规律:
振子的位移:指由平衡位置指向某一振动位置的有向线段。
x 都是相对于平衡位置的位移,以平衡位置为坐标原点O,沿振动方向建立坐标轴。
规定在O点右边时位移为正
在左边时位移为负。
为正
为负
怎样才能得到小球的位置与时刻的关系呢?
以小球的平衡位置为坐标原点,规定水平向右为正方向,横轴为时间 t,纵轴为位移 x。在坐标系中标出各时刻小球球心的位移,用曲线将其连接在一起,得到振动图像
描点作图法
得到的图像如图所示:
(1)全振动:如图,振子经历B→O→B’→O→B路径的一个____过程叫一次全振动。
(2)如右图,振子一直在平衡位置附近振动,每个全振动中偏离平衡位置的最大距离和需要的时间都__,振子的位移—时间函数为________,根据这个弹簧振子位置随时间变化的关系,从运动学上验证了简谐运动。
不变
完整振动
正弦或者余弦函数
5.弹簧振子的位移随时间变化规律:
(3)振幅:物体振动时离开平衡位置的____叫做振动的振幅,用A表示。
(4)周期:物体完成_____所需
要的时间叫做振动的周期,用 T 表示。
(5)频率:物体在一段时间内全振动
的__与所用__之比叫做振动的频率,用 f 表示。
【说明】对一般的周期与频率之间的关系是____。
最大距离
一次全振动
次数
时间
T·f=1
除此之外,还有着其他值得注意的物理量,如:
振幅(A)
周期(T)
归纳:从简谐振动图像中看到的量
①任意时刻对平衡位置的位移或位移对应的时刻
②振动周期T,振幅A
③任意时刻回复力和加速度的方向
④任意时刻的速度方向(看下一时刻的位置)
振幅(A)
周期(T)
物理量 运动过程 →O O→B B→O O→
位移 方向
大小
回复力F 加速度a 方向
大小
速度v 方向
大小
动能大小
势能大小
向右
减小
向左
减小
向左
增大
增大
减小
向左
增大
向右
增大
向左
减小
减小
增大
向左
减小
向右
减小
向右
增大
增大
减小
向右
增大
向左
增大
向右
减小
减小
增大
二、简谐运动的能量特征
思考:根据表格,可以分析得出什么结论?
1.在平衡位置,振子离开平衡位置的距离为零,所受回复力为零,加速度为零,速度最大,动能最大,弹性势能为零;
2.在最大振幅处,振子离开平衡位置的距离最大,所受回复力的大小最大,加速度的大小最大,速度为零,动能为零,弹性势能最大.
在回复力的作用下,振子在振动过程中离开平衡位置的距离、加速度、速度、动能、弹性势能等在每个周期里完全重复、这样的运动叫作周期性往复运动.
二、简谐运动的能量特征
1.物体做简谐运动的过程中,下列说法正确的是( )
A.当物体的位移减小时,其速度和加速度的方向一定相同
B.当物体的速度变化最快时,其动能最大
C.当物体的加速度与速度反向时,其回复力正在减小
D.在物体的动能相等的两个时刻,其加速度相同
A
2.如图甲所示为以O点为平衡位置,在A、B两点间做简谐运动的弹簧振子,图乙为这个弹簧振子的振动图像,以向右为正方向,由图可知下列说法中正确的是( )
A.在t=0.2 s时刻,弹簧振子运动
到O位置
B.在t=0.1 s与t=0.3 s两个时刻,
弹簧振子的速度相同
C.从t=0到t=0.2 s的时间内,弹簧振子的动能持续地减小
D.在t=0.2 s与t=0.6 s两个时刻,弹簧振子的加速度相同
C
3.(多选)如图是某一质点做简谐运动的图像,下列说法正确的是( )
A.在第1 s内,质点速度逐渐增大
B.在第2 s内,质点速度逐渐增大
C.在第3 s内,动能转化为势能
D.在第4 s内,动能转化为势能
BC
1、机械振动:物体在平衡位置(中心位置)两侧附近所做往复运动。通常简称为振动。
平衡位置:振子原来静止时的位置
2、弹簧振子理性化模型:不计阻力、弹簧的质量与小球相比可以忽略。
3、简谐运动:质点的位移与时间的关系遵从正弦或余弦函数的规律,即它的振动图象(x—t图象)是一条正弦或余弦曲线 。
第二章 机械振动
第1节 简谐运动
波动过后的琴弦
摩天大楼和琴弦都在来回的振动。
思考:这些运动他们都有些什么共同的特征?
物体在某个固定位置附近做重复的往返运动.
观察现象
1、了解机械振动和简谐运动的基础知识。
2、正确理解简谐运动x-t图象的物理意义,并学会分析简谐运动的图像。
3、理解简谐运动的能量特征
一、认识机械振动和简谐运动
1.机械振动
定义:物体(或物体的一部分)在一个位置附近做的往复运动称为机械振动,简称振动。
2.特征:
(1)中心位置(平衡位置)
(2)往复运动
振动物体静止时的位置
“对称性”
“周期性”
定义:
物体在与平衡位置的位移大小成正比,并且总指向平衡位置的回复力的作用下的振动,叫作简谐振动.
振子的位移-时间函数为正弦或者余弦函数,具有这种特征的运动叫作简谐运动.
简谐运动是最简单、最基本的振动
(2)动力学角度
(1)运动学角度
3.简谐运动
为什么弹簧和滑块的振动越来越弱?
把一个滑块装在弹簧的一端,弹簧的另一端固定,滑块在杆上能够自由滑动。把滑块拉向一侧,然后放开,它就左右运动起来。
①阻力(空气阻力、摩擦力…)
②弹簧本身的质量
4.实验:探究简谐运动
(1)理想化条件:
①不计阻力
②弹簧的质量远小于小球质量
③小球可看成质点
④弹簧始终在弹性限度内
我们把理想条件下,轻弹簧和小球(即振子)所组成的系统称为弹簧振子,它是简协运动的典型实例.
(2)平衡位置:
质点(振子)原来静止的位置
(振动方向上合力为0)
4.实验:探究简谐运动
振子在振动过程中的受力情况如何 力与位移关系是什么?
对弹簧振子进行受力分析,弹簧振子在振动过程中,所受的重力和支持力平衡,对振子的运动无影响.
影响振子运动的只有弹簧的弹力.
(3)振子在振动过程中的受力情况:
这个力的方向跟振子偏离平衡位置的位移方向相反,总指向平衡位置,它的作用是使振子能返回平衡位置,这个力叫作回复力.
FN
G
4.实验:探究简谐运动
F=-kx
振子所受回复力的大小跟振子偏离平衡位移的位移x的大小成正比。
实验结论:弹簧振子是在跟平衡位置的位移大小成正比并且总指向平衡位置的回复力的作用下的振动,从动力学上验证了简谐振动。
负号表示回复力的方向跟振子偏离平衡位置的位移方向相反。
即:
4.实验:探究简谐运动
5.弹簧振子的位移随时间变化规律:
振子的位移:指由平衡位置指向某一振动位置的有向线段。
x 都是相对于平衡位置的位移,以平衡位置为坐标原点O,沿振动方向建立坐标轴。
规定在O点右边时位移为正
在左边时位移为负。
为正
为负
怎样才能得到小球的位置与时刻的关系呢?
以小球的平衡位置为坐标原点,规定水平向右为正方向,横轴为时间 t,纵轴为位移 x。在坐标系中标出各时刻小球球心的位移,用曲线将其连接在一起,得到振动图像
描点作图法
得到的图像如图所示:
(1)全振动:如图,振子经历B→O→B’→O→B路径的一个____过程叫一次全振动。
(2)如右图,振子一直在平衡位置附近振动,每个全振动中偏离平衡位置的最大距离和需要的时间都__,振子的位移—时间函数为________,根据这个弹簧振子位置随时间变化的关系,从运动学上验证了简谐运动。
不变
完整振动
正弦或者余弦函数
5.弹簧振子的位移随时间变化规律:
(3)振幅:物体振动时离开平衡位置的____叫做振动的振幅,用A表示。
(4)周期:物体完成_____所需
要的时间叫做振动的周期,用 T 表示。
(5)频率:物体在一段时间内全振动
的__与所用__之比叫做振动的频率,用 f 表示。
【说明】对一般的周期与频率之间的关系是____。
最大距离
一次全振动
次数
时间
T·f=1
除此之外,还有着其他值得注意的物理量,如:
振幅(A)
周期(T)
归纳:从简谐振动图像中看到的量
①任意时刻对平衡位置的位移或位移对应的时刻
②振动周期T,振幅A
③任意时刻回复力和加速度的方向
④任意时刻的速度方向(看下一时刻的位置)
振幅(A)
周期(T)
物理量 运动过程 →O O→B B→O O→
位移 方向
大小
回复力F 加速度a 方向
大小
速度v 方向
大小
动能大小
势能大小
向右
减小
向左
减小
向左
增大
增大
减小
向左
增大
向右
增大
向左
减小
减小
增大
向左
减小
向右
减小
向右
增大
增大
减小
向右
增大
向左
增大
向右
减小
减小
增大
二、简谐运动的能量特征
思考:根据表格,可以分析得出什么结论?
1.在平衡位置,振子离开平衡位置的距离为零,所受回复力为零,加速度为零,速度最大,动能最大,弹性势能为零;
2.在最大振幅处,振子离开平衡位置的距离最大,所受回复力的大小最大,加速度的大小最大,速度为零,动能为零,弹性势能最大.
在回复力的作用下,振子在振动过程中离开平衡位置的距离、加速度、速度、动能、弹性势能等在每个周期里完全重复、这样的运动叫作周期性往复运动.
二、简谐运动的能量特征
1.物体做简谐运动的过程中,下列说法正确的是( )
A.当物体的位移减小时,其速度和加速度的方向一定相同
B.当物体的速度变化最快时,其动能最大
C.当物体的加速度与速度反向时,其回复力正在减小
D.在物体的动能相等的两个时刻,其加速度相同
A
2.如图甲所示为以O点为平衡位置,在A、B两点间做简谐运动的弹簧振子,图乙为这个弹簧振子的振动图像,以向右为正方向,由图可知下列说法中正确的是( )
A.在t=0.2 s时刻,弹簧振子运动
到O位置
B.在t=0.1 s与t=0.3 s两个时刻,
弹簧振子的速度相同
C.从t=0到t=0.2 s的时间内,弹簧振子的动能持续地减小
D.在t=0.2 s与t=0.6 s两个时刻,弹簧振子的加速度相同
C
3.(多选)如图是某一质点做简谐运动的图像,下列说法正确的是( )
A.在第1 s内,质点速度逐渐增大
B.在第2 s内,质点速度逐渐增大
C.在第3 s内,动能转化为势能
D.在第4 s内,动能转化为势能
BC
1、机械振动:物体在平衡位置(中心位置)两侧附近所做往复运动。通常简称为振动。
平衡位置:振子原来静止时的位置
2、弹簧振子理性化模型:不计阻力、弹簧的质量与小球相比可以忽略。
3、简谐运动:质点的位移与时间的关系遵从正弦或余弦函数的规律,即它的振动图象(x—t图象)是一条正弦或余弦曲线 。
同课章节目录
- 第一章 动量和动量守恒定律
- 第一节 冲量 动量
- 第二节 动量定理
- 第三节 动量守恒定律
- 第四节 动量守恒定律的应用
- 第五节 弹性碰撞与非弹性碰撞
- 第六节 自然界中的守恒定律
- 第二章 机械振动
- 第一节 简谐运动
- 第二节 简谐运动的描述
- 第三节 单摆
- 第四节 用单摆测量重力加速度
- 第五节 受迫振动 共振
- 第三章 机械波
- 第一节 机械波的产生和传播
- 第二节 机械波的描述
- 第三节 机械波的传播现象
- 第四节 多普勒效应
- 本章复习与测试
- 第四章 光及其应用
- 第一节 光的折射定律
- 第二节 测定介质的折射率
- 第三节 光的全反射与光纤技术
- 第四节 光的干涉
- 第五节 用双缝干涉实验测定光的波长
- 第六节 光的衍射和偏振
- 第七节 激光
