2.2 简谐运动的描述(20页)课件 2024-2025学年高二物理粤教版(2019)选择性必修第一册
文档属性
| 名称 | 2.2 简谐运动的描述(20页)课件 2024-2025学年高二物理粤教版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-04 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
第二章 机械振动
第2节 简谐运动的描述
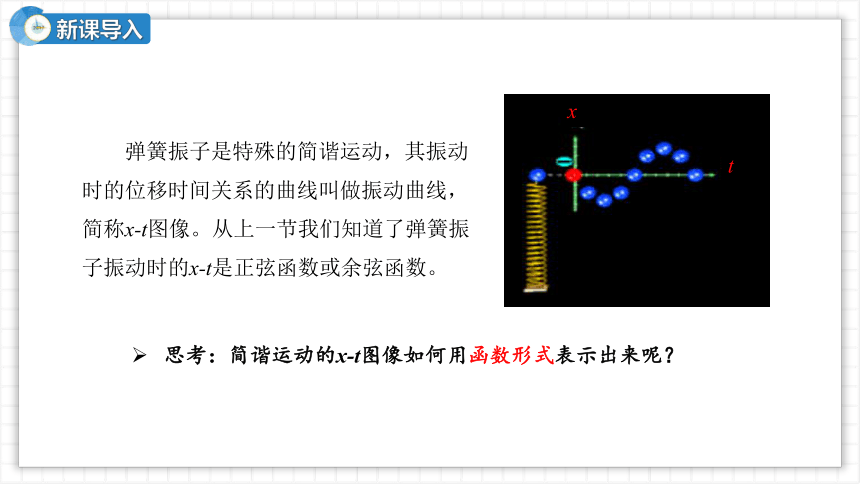
弹簧振子是特殊的简谐运动,其振动时的位移时间关系的曲线叫做振动曲线,简称x-t图像。从上一节我们知道了弹簧振子振动时的x-t是正弦函数或余弦函数。
x
t
思考:简谐运动的x-t图像如何用函数形式表示出来呢?
1.掌握通过函数描述简谐运动的方法
2.掌握通过图像描述简谐运动的方法
(1) 简谐运动的x-t图像反映的是质点偏离平衡位置的位移随时间变化的规律,并不是质点的运动轨迹,运动轨迹的长度也不是正弦或余弦图线拉开后的长度。
(2)在x- t图像上,质点在某时刻的位移,即为此时刻对应的纵坐标。
(3)质点在某段时间内的路程,需结合振动质点的实际运动轨迹进行计算。
(4)简谐运动位移—时间图像的函数表达式
一、简谐运动的函数描述
与简谐运动的函数有关的物理量有哪些呢?
1.简谐运动的位移-时间图象
2.振幅
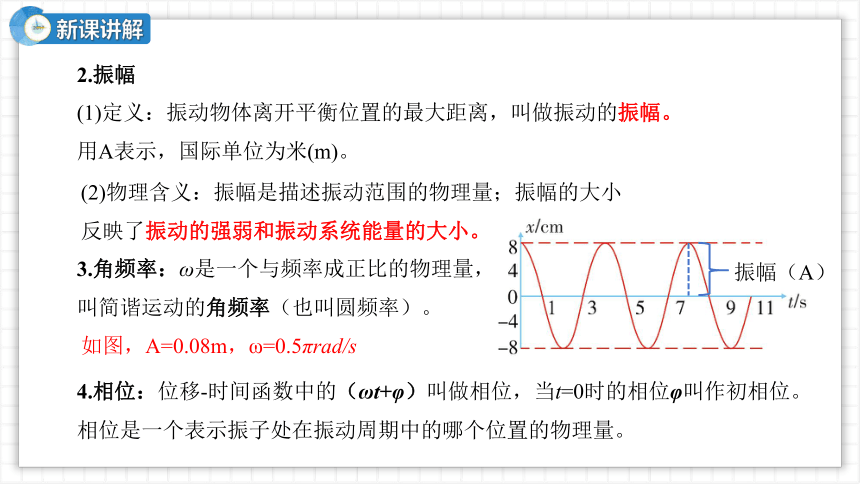
(1)定义:振动物体离开平衡位置的最大距离,叫做振动的振幅。用A表示,国际单位为米(m)。
(2)物理含义:振幅是描述振动范围的物理量;振幅的大小反映了振动的强弱和振动系统能量的大小。
3.角频率:ω是一个与频率成正比的物理量,叫简谐运动的角频率(也叫圆频率)。
如图,A=0.08m,ω=0.5πrad/s
4.相位:位移-时间函数中的(ωt+φ)叫做相位,当t=0时的相位φ叫作初相位。
相位是一个表示振子处在振动周期中的哪个位置的物理量。
振幅(A)
5.周期:
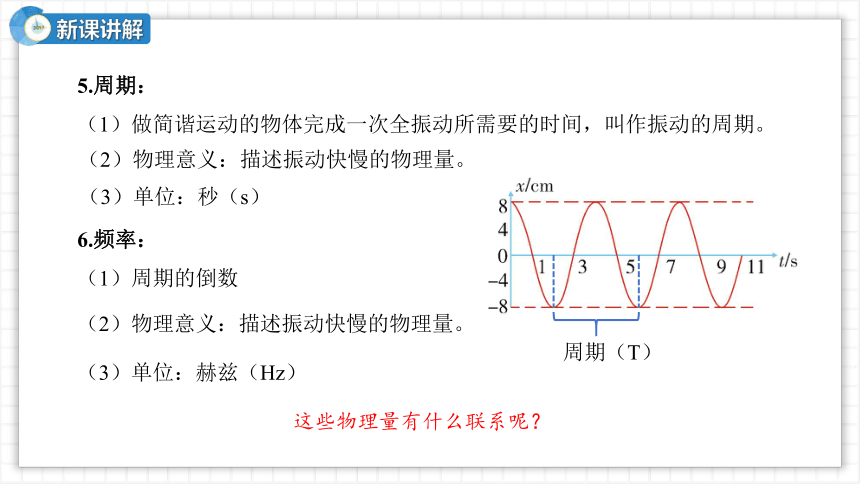
(1)做简谐运动的物体完成一次全振动所需要的时间,叫作振动的周期。
(2)物理意义:描述振动快慢的物理量。
(3)单位:秒(s)
6.频率:
(1)周期的倒数
(2)物理意义:描述振动快慢的物理量。
(3)单位:赫兹(Hz)
这些物理量有什么联系呢?
周期(T)
观看视频:弹簧振子与匀速圆周运动
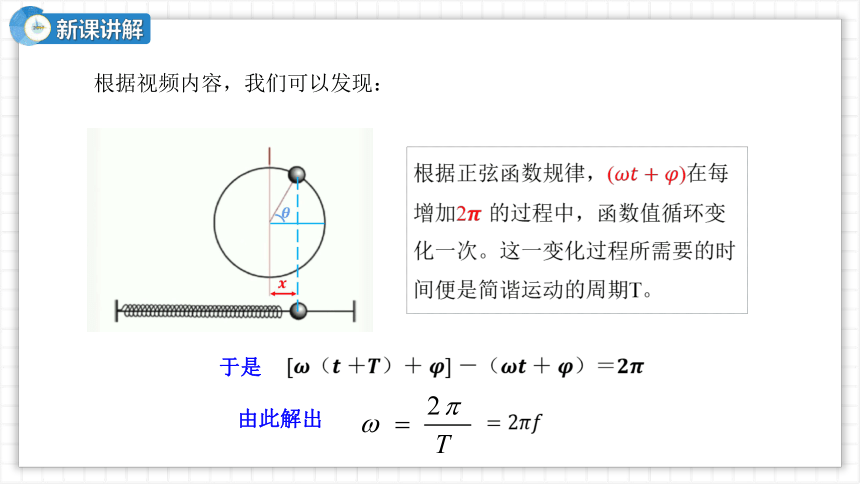
根据正弦函数规律,()在每增加2 的过程中,函数值循环变化一次。这一变化过程所需要的时间便是简谐运动的周期T。
于是
由此解出
根据视频内容,我们可以发现:
简谐运动的位移-时间关系:
若用正弦呢?
注意事项:
(1)振幅与位移:振动中的位移是矢量,振幅是标量.在数值上,振幅与振动物体的最大位移相等,在同一简谐运动中振幅是确定的,而位移随时间做周期性的变化.
(2)振幅与路程:振动中的路程是标量,是随时间不断增大的.其中常用的定量关系是:一个周期内的路程为4倍振幅,半个周期内的路程为2倍振幅.
(3)振幅与周期:在简谐运动中,一个确定的振动系统的周期(或频率)是固定的,与振幅无关.
二、简谐运动的图像描述
思考:如何根据简谐运动的函数判断两个
相同频率简谐运动的先后关系?
现有两个振子P、Q做简谐运动,从图像中可以分别看出两个简谐运动的振幅、周期、频率等物理量
二者振动的“步调”不同
P、Q做简谐运动的位移-时间函数表达式分别为
振子Q的位移在 3/4T 时刻达到正向最大值
振子P 的位移在 T 时刻才达到正向最大值
∴ 振子Q的振动比振子P超前了1/4T
Q的振动与P的振动有的相位差
振子做简谐运动的位移-时间函数表达式为
相位每增加2,振子完成一次全振动
相位:
初相位:t =0 时的相位
位移随时间的变化完全由相位决定
相位是表示振子处在振动周期中的哪个位置的物理量
二、简谐运动的图像描述
两个振子做简谐运动
相位差:
对于频率相同、相位不同的振子,通过对比二者的相位差来比较振动先后的关系.
相位是一个相对概念,与所取的时间零点有关;
相位差是个绝对概念,表示两个频率相同的简谐运动的振动先后关系.
关于相位差的说明:
(1)取值范围:-2π ≤ ≤ 2π.
(2) >0,表示振动2比振动1超前.
<0,表示振动2比振动1滞后.
①同相:相位差为零,一般地为
②反相:相位差为 ,一般地为
1. (多选)如图是一做简谐运动的物体的振动图像,下列说法正确的是( )
A.振动周期是2×10-2 s
B.物体振动的频率为25 Hz
C.物体振动的振幅为10 cm
D.在6×10-2 s内通过的路程是60 cm
BCD
2. 如图所示,弹簧振子在振动过程中,振子经过a、b两点时的速度相同,若它从a经O到b历时0.2 s,然后从b再回到a的最短时间为0.4 s,则该振子的振动频率为( )
A.1 Hz
B.1.25 Hz
C.2 Hz
D.2.5 Hz
B
3.(多选)弹簧振子以O点为平衡位置做简谐运动,从振子通过O点时开始计时,振子第一次到达M点用了0.3 s,又经过0.2 s第二次通过M点,则振子第三次通过M点还要经过的时间可能是( )
A. s
B. s
C.1.4 s
D.1.6 s
AC
4. (多选)一弹簧振子A的位移y随时间t变化的关系式为y=0.1sin(2.5πt) m。则( )
A.弹簧振子的振幅为0.2 m
B.弹簧振子的周期为1.25 s
C.在t=0.2 s时,振子的运动速度为零
D.若另一弹簧振子B的位移y随时间变化的关系式为 ,则振动A滞后振动B的相位为
CD
函数描述 :x=Acos(ωt+φ)
也可以写成:
根据一个简谐运动的振幅、周期、初相位,可以知道做简谐运动的物体在任意时刻的位移,故振幅、周期、初相位是描述简谐运动特征的物理量。
位移
振幅
圆频率ω=2π/T=2πf
初相位
相位
时刻
简谐运动的描述
第二章 机械振动
第2节 简谐运动的描述
弹簧振子是特殊的简谐运动,其振动时的位移时间关系的曲线叫做振动曲线,简称x-t图像。从上一节我们知道了弹簧振子振动时的x-t是正弦函数或余弦函数。
x
t
思考:简谐运动的x-t图像如何用函数形式表示出来呢?
1.掌握通过函数描述简谐运动的方法
2.掌握通过图像描述简谐运动的方法
(1) 简谐运动的x-t图像反映的是质点偏离平衡位置的位移随时间变化的规律,并不是质点的运动轨迹,运动轨迹的长度也不是正弦或余弦图线拉开后的长度。
(2)在x- t图像上,质点在某时刻的位移,即为此时刻对应的纵坐标。
(3)质点在某段时间内的路程,需结合振动质点的实际运动轨迹进行计算。
(4)简谐运动位移—时间图像的函数表达式
一、简谐运动的函数描述
与简谐运动的函数有关的物理量有哪些呢?
1.简谐运动的位移-时间图象
2.振幅
(1)定义:振动物体离开平衡位置的最大距离,叫做振动的振幅。用A表示,国际单位为米(m)。
(2)物理含义:振幅是描述振动范围的物理量;振幅的大小反映了振动的强弱和振动系统能量的大小。
3.角频率:ω是一个与频率成正比的物理量,叫简谐运动的角频率(也叫圆频率)。
如图,A=0.08m,ω=0.5πrad/s
4.相位:位移-时间函数中的(ωt+φ)叫做相位,当t=0时的相位φ叫作初相位。
相位是一个表示振子处在振动周期中的哪个位置的物理量。
振幅(A)
5.周期:
(1)做简谐运动的物体完成一次全振动所需要的时间,叫作振动的周期。
(2)物理意义:描述振动快慢的物理量。
(3)单位:秒(s)
6.频率:
(1)周期的倒数
(2)物理意义:描述振动快慢的物理量。
(3)单位:赫兹(Hz)
这些物理量有什么联系呢?
周期(T)
观看视频:弹簧振子与匀速圆周运动
根据正弦函数规律,()在每增加2 的过程中,函数值循环变化一次。这一变化过程所需要的时间便是简谐运动的周期T。
于是
由此解出
根据视频内容,我们可以发现:
简谐运动的位移-时间关系:
若用正弦呢?
注意事项:
(1)振幅与位移:振动中的位移是矢量,振幅是标量.在数值上,振幅与振动物体的最大位移相等,在同一简谐运动中振幅是确定的,而位移随时间做周期性的变化.
(2)振幅与路程:振动中的路程是标量,是随时间不断增大的.其中常用的定量关系是:一个周期内的路程为4倍振幅,半个周期内的路程为2倍振幅.
(3)振幅与周期:在简谐运动中,一个确定的振动系统的周期(或频率)是固定的,与振幅无关.
二、简谐运动的图像描述
思考:如何根据简谐运动的函数判断两个
相同频率简谐运动的先后关系?
现有两个振子P、Q做简谐运动,从图像中可以分别看出两个简谐运动的振幅、周期、频率等物理量
二者振动的“步调”不同
P、Q做简谐运动的位移-时间函数表达式分别为
振子Q的位移在 3/4T 时刻达到正向最大值
振子P 的位移在 T 时刻才达到正向最大值
∴ 振子Q的振动比振子P超前了1/4T
Q的振动与P的振动有的相位差
振子做简谐运动的位移-时间函数表达式为
相位每增加2,振子完成一次全振动
相位:
初相位:t =0 时的相位
位移随时间的变化完全由相位决定
相位是表示振子处在振动周期中的哪个位置的物理量
二、简谐运动的图像描述
两个振子做简谐运动
相位差:
对于频率相同、相位不同的振子,通过对比二者的相位差来比较振动先后的关系.
相位是一个相对概念,与所取的时间零点有关;
相位差是个绝对概念,表示两个频率相同的简谐运动的振动先后关系.
关于相位差的说明:
(1)取值范围:-2π ≤ ≤ 2π.
(2) >0,表示振动2比振动1超前.
<0,表示振动2比振动1滞后.
①同相:相位差为零,一般地为
②反相:相位差为 ,一般地为
1. (多选)如图是一做简谐运动的物体的振动图像,下列说法正确的是( )
A.振动周期是2×10-2 s
B.物体振动的频率为25 Hz
C.物体振动的振幅为10 cm
D.在6×10-2 s内通过的路程是60 cm
BCD
2. 如图所示,弹簧振子在振动过程中,振子经过a、b两点时的速度相同,若它从a经O到b历时0.2 s,然后从b再回到a的最短时间为0.4 s,则该振子的振动频率为( )
A.1 Hz
B.1.25 Hz
C.2 Hz
D.2.5 Hz
B
3.(多选)弹簧振子以O点为平衡位置做简谐运动,从振子通过O点时开始计时,振子第一次到达M点用了0.3 s,又经过0.2 s第二次通过M点,则振子第三次通过M点还要经过的时间可能是( )
A. s
B. s
C.1.4 s
D.1.6 s
AC
4. (多选)一弹簧振子A的位移y随时间t变化的关系式为y=0.1sin(2.5πt) m。则( )
A.弹簧振子的振幅为0.2 m
B.弹簧振子的周期为1.25 s
C.在t=0.2 s时,振子的运动速度为零
D.若另一弹簧振子B的位移y随时间变化的关系式为 ,则振动A滞后振动B的相位为
CD
函数描述 :x=Acos(ωt+φ)
也可以写成:
根据一个简谐运动的振幅、周期、初相位,可以知道做简谐运动的物体在任意时刻的位移,故振幅、周期、初相位是描述简谐运动特征的物理量。
位移
振幅
圆频率ω=2π/T=2πf
初相位
相位
时刻
简谐运动的描述
同课章节目录
- 第一章 动量和动量守恒定律
- 第一节 冲量 动量
- 第二节 动量定理
- 第三节 动量守恒定律
- 第四节 动量守恒定律的应用
- 第五节 弹性碰撞与非弹性碰撞
- 第六节 自然界中的守恒定律
- 第二章 机械振动
- 第一节 简谐运动
- 第二节 简谐运动的描述
- 第三节 单摆
- 第四节 用单摆测量重力加速度
- 第五节 受迫振动 共振
- 第三章 机械波
- 第一节 机械波的产生和传播
- 第二节 机械波的描述
- 第三节 机械波的传播现象
- 第四节 多普勒效应
- 本章复习与测试
- 第四章 光及其应用
- 第一节 光的折射定律
- 第二节 测定介质的折射率
- 第三节 光的全反射与光纤技术
- 第四节 光的干涉
- 第五节 用双缝干涉实验测定光的波长
- 第六节 光的衍射和偏振
- 第七节 激光
