1.4一次函数与一元二次方程的联系 同步练习(含答案)
文档属性
| 名称 | 1.4一次函数与一元二次方程的联系 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 218.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
1.4一次函数与一元二次方程的联系
一、填空题
1.如图,抛物线的顶点为C,与x轴交于A,B两点,则 .
2.如图,抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.将抛物线沿y轴向下平移t(t>0)个单位,当平移后的抛物线与线段OB有且只有一个交点时,则t的取值范围是 .
3.如图是二次函数和一次函数的图象,当时,x的取值范围是 .
4.已知抛物线与轴的一个交点为,则代数式的值为 .
5.抛物线与y轴交点的纵坐标是 .
6.直线和抛物线(是常数,且)在同一平面直角坐标系中,直线经过点.下列结论:
①抛物线的对称轴是直线;
②抛物线与轴一定有两个交点;
③关于的方程有两个根;
④若,当或时,;
其中正确的结论是 .(填序号)
二、单选题
7.已知二次函数的变量,的部分对应值如表:
x … 0 1 …
y … 1 1 …
根据表中信息,可得一元二次方程的一个近似解的范围是( )
A. B.
C. D.
8.已知二次函数的部分图象如图所示,图象经过点,其对称轴为直线.下列结论:①;②;③若点均在二次函数图象上,则;④关于x的一元二次方程有两个相等的实数根:⑤若是方程的两根,则方程的两根,满足其中正确结论的个数为( )
A.2个 B.3个 C.4个 D.5个
9.抛物线与轴的交点坐标是( )
A. B. C. D.
10.在平面直角坐标系中,二次函数的图像与轴的一个交点的横坐标为3,则另一个交点的横坐标为( )
A. B. C. D.1
11.已知抛物线的图象如图所示,对称轴是直线,下列结论:①;②;③;④.其中正确的是( )
A.①②③ B.③③④ C.①②④ D.①②③④
三、解答题
12.已知二次函数.
(1)将二次函数化成顶点式;
(2)求图像与轴,轴的交点坐标.
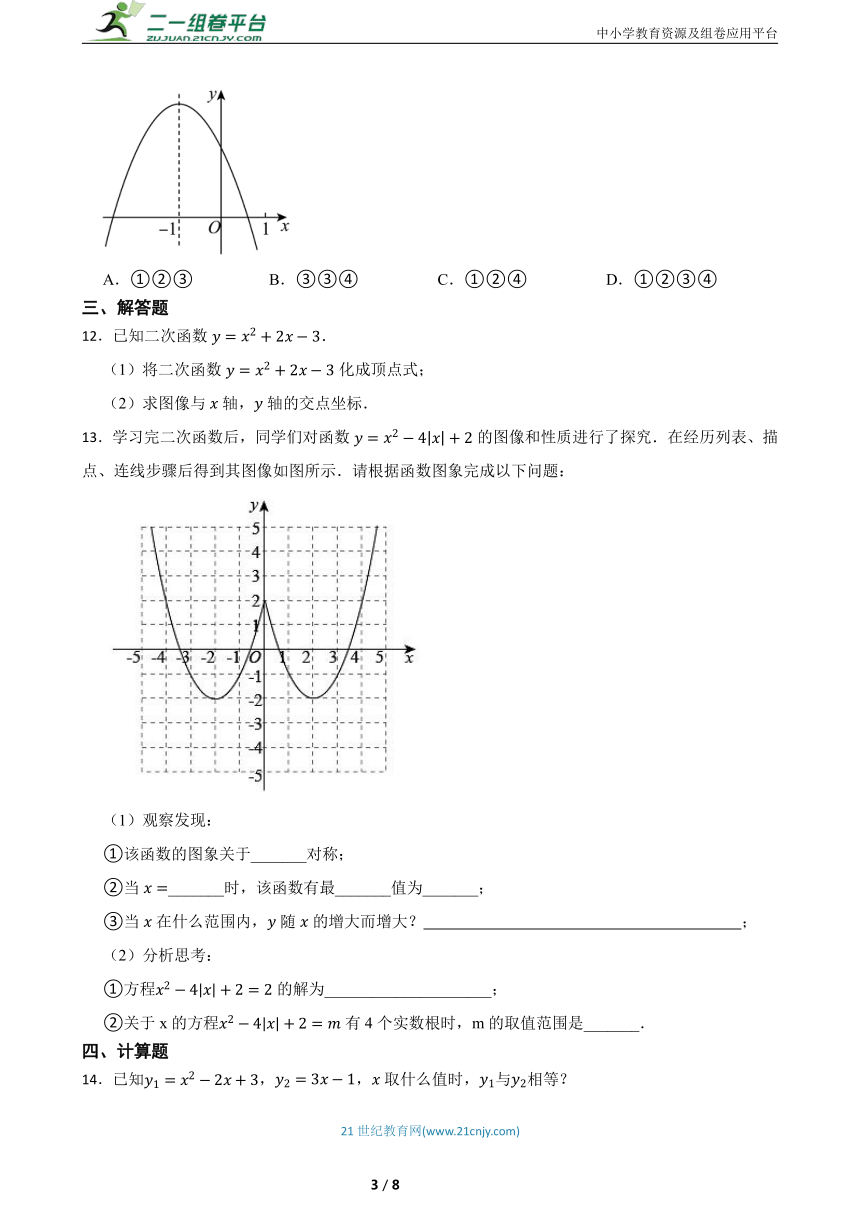
13.学习完二次函数后,同学们对函数的图像和性质进行了探究.在经历列表、描点、连线步骤后得到其图像如图所示.请根据函数图象完成以下问题:
(1)观察发现:
①该函数的图象关于_______对称;
②当_______时,该函数有最_______值为_______;
③当在什么范围内,随的增大而增大? ;
(2)分析思考:
①方程的解为_____________________;
②关于x的方程有4个实数根时,m的取值范围是_______.
四、计算题
14.已知,,取什么值时,与相等?
15.【定义】若抛物线与一水平直线交于两点,我们把这两点间线段的长称为抛物线关于这条直线的跨径,抛物线的顶点到该直线的距离称为抛物线关于这条直线的矢高,矢高与跨径的比值称为抛物线关于这条直线的矢跨比.如图1,抛物线的顶点为轴于点,它与轴交于点,则的长为抛物线关于轴的跨径,的长为抛物线关于轴的矢高,的值为抛物线关于轴的矢跨比.
(1)【特例】如图2,已知抛物线与轴交于点(点在点右侧)抛物线关于轴的矢高是______,跨径是______,矢跨比是______;
(2)【应用】如图3是某地一座三连拱桥梁建筑示意图,其中主跨与边跨的拱轴线为开口方向与大小一样的抛物线,它们关于水平钢梁所在直线的跨径分别为420米与280米,已知主跨的矢跨比为,请求出边跨的矢跨比.
五、综合题
16.已知抛物线y=x2+(k﹣5)x﹣(k+4),
(1)求证:抛物线与x轴必有两个交点;
(2)若该抛物线与x轴的两个交点为A(x1,0)、B(x2,0),且(x1+1)(x2+1)=﹣8,求二次函数的解析式.
17.已知二次函数 .
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
18.已知在平面直角坐标系内,抛物线y=x2+bx+6经过x轴上两点A, B,点B的坐标为(3,0),与y轴相交于点C;
(1)求抛物线的表达式;
(2)求△ABC的面积.
答案解析部分
1.【答案】27
【知识点】二次函数图象与坐标轴的交点问题
2.【答案】0<t<3或t=4
【知识点】二次函数图象的几何变换;二次函数图象与坐标轴的交点问题
3.【答案】或
【知识点】二次函数与不等式(组)的综合应用
4.【答案】-1
【知识点】代数式求值;二次函数图象与坐标轴的交点问题
5.【答案】0
【知识点】二次函数图象与坐标轴的交点问题
6.【答案】①②③
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
7.【答案】C
【知识点】利用二次函数图象求一元二次方程的近似根
8.【答案】A
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;利用二次函数图象判断一元二次方程根的情况
9.【答案】B
【知识点】二次函数图象与坐标轴的交点问题
10.【答案】C
【知识点】二次函数图象与坐标轴的交点问题
11.【答案】D
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
12.【答案】(1)
(2)与轴交于点,与轴交于点,
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
13.【答案】(1)①轴;②或2,小,;③或
(2)①,,;②
【知识点】二次函数与不等式(组)的综合应用;利用二次函数图象判断一元二次方程根的情况
14.【答案】当为1或4时,与相等
【知识点】二次函数图象与坐标轴的交点问题
15.【答案】(1)9;6;
(2)
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
16.【答案】(1)证明:△=(k﹣5)2+4(k+4)
=k2﹣6k+41
=(k﹣3)2+32,
∵(k﹣3)2≥0,
∴△>0, ∴抛物线与x轴必有两个交点;
(2)解:根据题意得x1、x2为方程x2+(k﹣5)x﹣(k+4)=0的两根,
∴x1+x2=﹣(k﹣5),
x1 x2=﹣(k+4),
∵(x1+1)(x2+1)=﹣8,
∴x1 x2+x1+x2+1=﹣8,
即﹣(k+4)﹣(k﹣5)+1=﹣8,解得k=5,
∴二次函数的解析式为y=x2﹣9.
【知识点】二次函数图象与坐标轴的交点问题;利用二次函数图象求一元二次方程的近似根
17.【答案】(1)解:∵二次函数的图象与x轴有两个交点,∴△= ,∴m>﹣1;
(2)解:∵二次函数的图象过点A(3,0),∴0=﹣9+6+m,∴m=3,∴二次函数的解析式为: ,令x=0,则y=3,∴B(0,3),设直线AB的解析式为: ,∴ ,解得: ,∴直线AB的解析式为: ,∵抛物线 的对称轴为:x=1,∴ ,解得: ,∴P(1,2).
【知识点】待定系数法求一次函数解析式;二次函数图象与坐标轴的交点问题
18.【答案】(1)解:把点B的坐标(3,0)代入抛物线y=x2+bx+6得0=9+3b+6,解得b=-5,所以抛物线的表达式y=x2-5x+6;
(2)解:∵抛物线的表达式为
当 时, 即就是
解得
当 时,
【知识点】二次函数图象与坐标轴的交点问题
21世纪教育网(www.21cnjy.com)
8 / 8
1.4一次函数与一元二次方程的联系
一、填空题
1.如图,抛物线的顶点为C,与x轴交于A,B两点,则 .
2.如图,抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.将抛物线沿y轴向下平移t(t>0)个单位,当平移后的抛物线与线段OB有且只有一个交点时,则t的取值范围是 .
3.如图是二次函数和一次函数的图象,当时,x的取值范围是 .
4.已知抛物线与轴的一个交点为,则代数式的值为 .
5.抛物线与y轴交点的纵坐标是 .
6.直线和抛物线(是常数,且)在同一平面直角坐标系中,直线经过点.下列结论:
①抛物线的对称轴是直线;
②抛物线与轴一定有两个交点;
③关于的方程有两个根;
④若,当或时,;
其中正确的结论是 .(填序号)
二、单选题
7.已知二次函数的变量,的部分对应值如表:
x … 0 1 …
y … 1 1 …
根据表中信息,可得一元二次方程的一个近似解的范围是( )
A. B.
C. D.
8.已知二次函数的部分图象如图所示,图象经过点,其对称轴为直线.下列结论:①;②;③若点均在二次函数图象上,则;④关于x的一元二次方程有两个相等的实数根:⑤若是方程的两根,则方程的两根,满足其中正确结论的个数为( )
A.2个 B.3个 C.4个 D.5个
9.抛物线与轴的交点坐标是( )
A. B. C. D.
10.在平面直角坐标系中,二次函数的图像与轴的一个交点的横坐标为3,则另一个交点的横坐标为( )
A. B. C. D.1
11.已知抛物线的图象如图所示,对称轴是直线,下列结论:①;②;③;④.其中正确的是( )
A.①②③ B.③③④ C.①②④ D.①②③④
三、解答题
12.已知二次函数.
(1)将二次函数化成顶点式;
(2)求图像与轴,轴的交点坐标.
13.学习完二次函数后,同学们对函数的图像和性质进行了探究.在经历列表、描点、连线步骤后得到其图像如图所示.请根据函数图象完成以下问题:
(1)观察发现:
①该函数的图象关于_______对称;
②当_______时,该函数有最_______值为_______;
③当在什么范围内,随的增大而增大? ;
(2)分析思考:
①方程的解为_____________________;
②关于x的方程有4个实数根时,m的取值范围是_______.
四、计算题
14.已知,,取什么值时,与相等?
15.【定义】若抛物线与一水平直线交于两点,我们把这两点间线段的长称为抛物线关于这条直线的跨径,抛物线的顶点到该直线的距离称为抛物线关于这条直线的矢高,矢高与跨径的比值称为抛物线关于这条直线的矢跨比.如图1,抛物线的顶点为轴于点,它与轴交于点,则的长为抛物线关于轴的跨径,的长为抛物线关于轴的矢高,的值为抛物线关于轴的矢跨比.
(1)【特例】如图2,已知抛物线与轴交于点(点在点右侧)抛物线关于轴的矢高是______,跨径是______,矢跨比是______;
(2)【应用】如图3是某地一座三连拱桥梁建筑示意图,其中主跨与边跨的拱轴线为开口方向与大小一样的抛物线,它们关于水平钢梁所在直线的跨径分别为420米与280米,已知主跨的矢跨比为,请求出边跨的矢跨比.
五、综合题
16.已知抛物线y=x2+(k﹣5)x﹣(k+4),
(1)求证:抛物线与x轴必有两个交点;
(2)若该抛物线与x轴的两个交点为A(x1,0)、B(x2,0),且(x1+1)(x2+1)=﹣8,求二次函数的解析式.
17.已知二次函数 .
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
18.已知在平面直角坐标系内,抛物线y=x2+bx+6经过x轴上两点A, B,点B的坐标为(3,0),与y轴相交于点C;
(1)求抛物线的表达式;
(2)求△ABC的面积.
答案解析部分
1.【答案】27
【知识点】二次函数图象与坐标轴的交点问题
2.【答案】0<t<3或t=4
【知识点】二次函数图象的几何变换;二次函数图象与坐标轴的交点问题
3.【答案】或
【知识点】二次函数与不等式(组)的综合应用
4.【答案】-1
【知识点】代数式求值;二次函数图象与坐标轴的交点问题
5.【答案】0
【知识点】二次函数图象与坐标轴的交点问题
6.【答案】①②③
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
7.【答案】C
【知识点】利用二次函数图象求一元二次方程的近似根
8.【答案】A
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;利用二次函数图象判断一元二次方程根的情况
9.【答案】B
【知识点】二次函数图象与坐标轴的交点问题
10.【答案】C
【知识点】二次函数图象与坐标轴的交点问题
11.【答案】D
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
12.【答案】(1)
(2)与轴交于点,与轴交于点,
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
13.【答案】(1)①轴;②或2,小,;③或
(2)①,,;②
【知识点】二次函数与不等式(组)的综合应用;利用二次函数图象判断一元二次方程根的情况
14.【答案】当为1或4时,与相等
【知识点】二次函数图象与坐标轴的交点问题
15.【答案】(1)9;6;
(2)
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
16.【答案】(1)证明:△=(k﹣5)2+4(k+4)
=k2﹣6k+41
=(k﹣3)2+32,
∵(k﹣3)2≥0,
∴△>0, ∴抛物线与x轴必有两个交点;
(2)解:根据题意得x1、x2为方程x2+(k﹣5)x﹣(k+4)=0的两根,
∴x1+x2=﹣(k﹣5),
x1 x2=﹣(k+4),
∵(x1+1)(x2+1)=﹣8,
∴x1 x2+x1+x2+1=﹣8,
即﹣(k+4)﹣(k﹣5)+1=﹣8,解得k=5,
∴二次函数的解析式为y=x2﹣9.
【知识点】二次函数图象与坐标轴的交点问题;利用二次函数图象求一元二次方程的近似根
17.【答案】(1)解:∵二次函数的图象与x轴有两个交点,∴△= ,∴m>﹣1;
(2)解:∵二次函数的图象过点A(3,0),∴0=﹣9+6+m,∴m=3,∴二次函数的解析式为: ,令x=0,则y=3,∴B(0,3),设直线AB的解析式为: ,∴ ,解得: ,∴直线AB的解析式为: ,∵抛物线 的对称轴为:x=1,∴ ,解得: ,∴P(1,2).
【知识点】待定系数法求一次函数解析式;二次函数图象与坐标轴的交点问题
18.【答案】(1)解:把点B的坐标(3,0)代入抛物线y=x2+bx+6得0=9+3b+6,解得b=-5,所以抛物线的表达式y=x2-5x+6;
(2)解:∵抛物线的表达式为
当 时, 即就是
解得
当 时,
【知识点】二次函数图象与坐标轴的交点问题
21世纪教育网(www.21cnjy.com)
8 / 8
