第一章二次函数综合检测题(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第一章二次函数综合检测题
一、填空题
1.已知抛物线y=ax2+bx+8经过点(3,2),则代数式3a+b+8的值为 .
2.若二次函数的图象经过原点,则m= .
3.抛物线y=2(x﹣3)2+1的顶点坐标是
4.抛物线与x轴的公共点是,则这条抛物线的对称轴是直线= .
5.为了在比赛中取得更好的成绩,运动员小明积极训练,教练对小明投掷铅球的录像进行技术分析,如图,发现铅球在行进过程中高度y(m)与水平距离x(m)之间的关系为,由此可知小明此次投掷的成绩是 m.
6.如图,正方形的边长为2,点在边上运动(不与点、重合),,点在射线上,且,与相交于点,连接、、.则下列结论:①;②;③;④面积的最大值为,其中正确结论的序号为 .
二、单选题
7.将抛物线先向右平移3个单位长度,再向下平移2个单位长度得到的新抛物线解析式为( )
A. B.
C. D.
8.把二次函数y=x2﹣4x+3化成y=a(x+h)2+k的形式是( )
A.y=(x+2)2+1 B.y=(x+2)2+7
C.y=(x﹣2)2﹣1 D.y=(x+2)2﹣7
9.下列函数中,属于二次函数的是( )
A. B. C. D.
10.抛物线 的顶点坐标为( )
A. B. C. D.
11.将抛物线y=3x2向右平移3个单位,所得到的抛物线是( )
A.y=3x2+3 B.y=3(x-3)2
C.y=3x2-3 D.y=3(x+3)2
12.以x为自变量的二次函数y= x2-2(b-2)x+ b2-1的 图象不经过第三象限,则实数b的取值范围是( )
A.b≧ B.b≧1或b≦-1 C.b≧2 D.1≦ b≦2
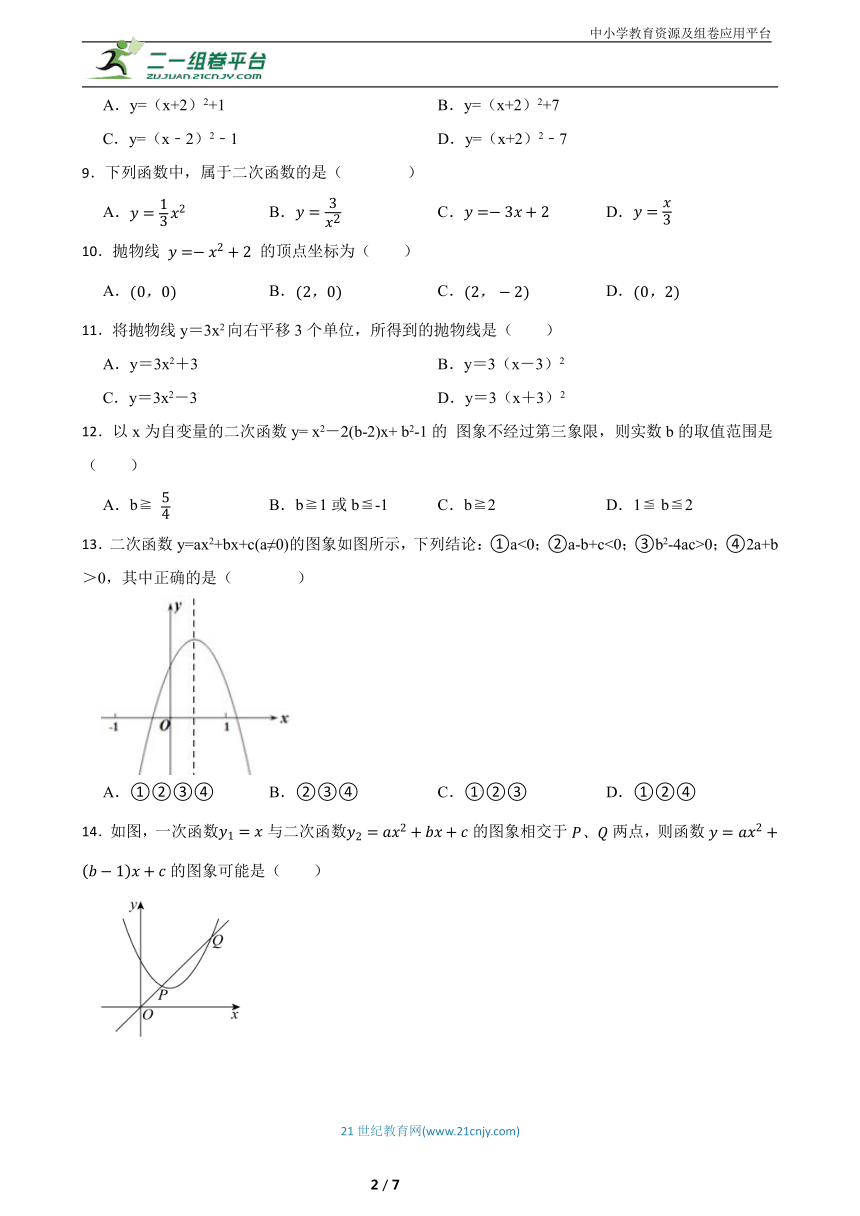
13.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①a<0;②a-b+c<0;③b2-4ac>0;④2a+b>0,其中正确的是( )
A.①②③④ B.②③④ C.①②③ D.①②④
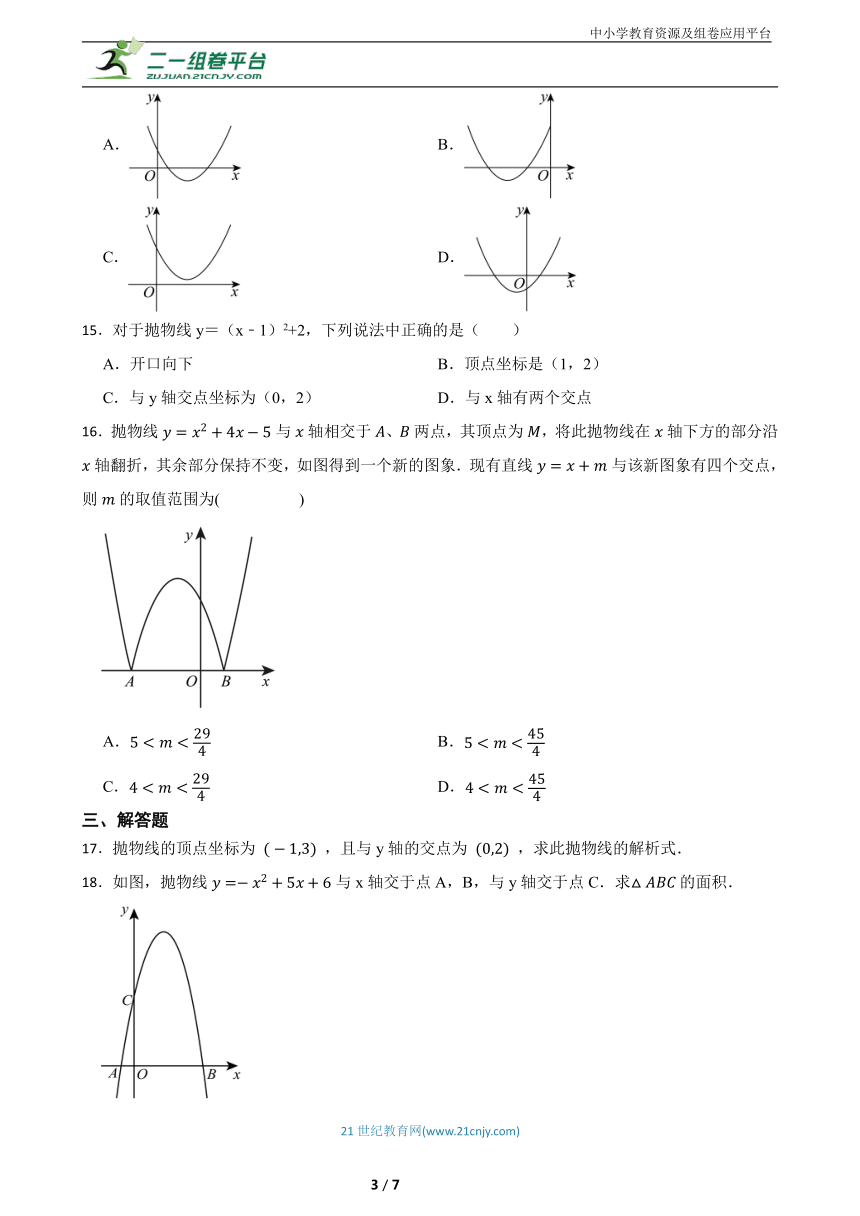
14.如图,一次函数与二次函数的图象相交于两点,则函数的图象可能是( )
A. B.
C. D.
15.对于抛物线y=(x﹣1)2+2,下列说法中正确的是( )
A.开口向下 B.顶点坐标是(1,2)
C.与y轴交点坐标为(0,2) D.与x轴有两个交点
16.抛物线与轴相交于、两点,其顶点为,将此抛物线在轴下方的部分沿轴翻折,其余部分保持不变,如图得到一个新的图象.现有直线与该新图象有四个交点,则的取值范围为( )
A. B.
C. D.
三、解答题
17.抛物线的顶点坐标为 ,且与y轴的交点为 ,求此抛物线的解析式.
18.如图,抛物线与x轴交于点A,B,与y轴交于点C.求的面积.
19.小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x是多少时,矩形场地面积S最大,最大面积是多少?
20.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点左侧,B点的坐标为(4,0),与y轴交于C(0,﹣4)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP'C,那么是否存在点P,使四边形POP'C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
四、计算题
21.已知:二次函数的图象经过点.
(1)求b的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
22.根据以下素材,探索完成任务.
如何设计打印图纸方案?
素材1 如图1,正方形是一张用于打印产品的示意图,它由三个区块(Ⅰ,Ⅱ,Ⅲ)构成.已知,点E,F分别在和上,且,设.
素材2 为了打印精准,拟在图2中的边上设置一排间距为1cm的定位坐标(B为坐标原点),计算机可根据点E的定位坐标精准打印出图案.
问题解决
任务1 确定关系 用x的代数式表示: 区域Ⅰ的面积=______;区域Ⅱ的面积=______.
任务2 拟定方案 为了美观,拟将区域Ⅲ分割为甲、乙两个三角形区域,并要求区域乙是含边的三角形,求所有方案中乙的面积或者函数表达式.
任务3 优化设计 经调查发现当且x为整数时,此时称E点为合格定位点.当区域乙的面积最小时,合格定位点E点为最佳定位点,求出最佳定位点E的坐标.
23.如图1,已知二次函数图象与轴交点为,其顶点为.
(1)求二次函数的表达式;
(2)直线与轴交于,现将线段上下移动,若线段与二次函数的图象有交点,求向上和向下平移的最大距离;
(3)若将(1)中二次函数图象平移,使其顶点与原点重合,然后将其图象绕点顺时针旋转,得到抛物线,如图2所示,直线与交于,两点,为上位于直线左侧一点,求面积最大值,及此时点的坐标.
答案解析部分
1.【答案】6
【知识点】二次函数图象上点的坐标特征
2.【答案】2
【知识点】二次函数的定义
3.【答案】(3,1)
【知识点】二次函数y=a(x-h)²+k的性质
4.【答案】2
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=ax²+bx+c的图象
5.【答案】9
【知识点】直接开平方法解一元二次方程;二次函数的实际应用-抛球问题
6.【答案】①②④
【知识点】二次函数的最值;三角形全等及其性质;勾股定理;正方形的性质
7.【答案】C
【知识点】二次函数图象的几何变换
8.【答案】C
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
9.【答案】A
【知识点】二次函数的定义
10.【答案】D
【知识点】二次函数y=a(x-h)²+k的图象
11.【答案】B
【知识点】二次函数图象的几何变换
12.【答案】C
【知识点】二次函数图象上点的坐标特征
13.【答案】C
【知识点】二次函数图象与系数的关系;二次函数y=ax²+bx+c的性质
14.【答案】A
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
15.【答案】B
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=a(x-h)²+k的图象
16.【答案】B
【知识点】一元二次方程根的判别式及应用;待定系数法求一次函数解析式;二次函数图象与坐标轴的交点问题
17.【答案】解:∵抛物线的顶点坐标为 ,
∴设抛物线解析式为 ,
把 代入得 ,
解得 ,
∴抛物线解析式为 .
【知识点】待定系数法求二次函数解析式
18.【答案】21
【知识点】二次函数图象与坐标轴的交点问题
19.【答案】(1)、S=x(30﹣x)(0<x<30);(2)、x=15时,S有最大值为225平方米.
【知识点】二次函数的实际应用-几何问题
20.【答案】(1);(2);(3)当x=2时,四边形ABPC的面积最大,此时P点的坐标为:(2,﹣6),四边形ABPC的面积的最大值为18.
【知识点】二次函数的最值;待定系数法求二次函数解析式;菱形的判定与性质
21.【答案】(1)
(2),
【知识点】待定系数法求二次函数解析式;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
22.【答案】任务一:区块Ⅰ的面积:,区块Ⅱ的面积:;任务二:或;任务三:
【知识点】二次函数的实际应用-几何问题
23.【答案】(1)
(2)CM向下平移的最大距离为,向上平移的最大距离为6.
(3)
【知识点】待定系数法求二次函数解析式;旋转的性质
21世纪教育网(www.21cnjy.com)
2 / 7
第一章二次函数综合检测题
一、填空题
1.已知抛物线y=ax2+bx+8经过点(3,2),则代数式3a+b+8的值为 .
2.若二次函数的图象经过原点,则m= .
3.抛物线y=2(x﹣3)2+1的顶点坐标是
4.抛物线与x轴的公共点是,则这条抛物线的对称轴是直线= .
5.为了在比赛中取得更好的成绩,运动员小明积极训练,教练对小明投掷铅球的录像进行技术分析,如图,发现铅球在行进过程中高度y(m)与水平距离x(m)之间的关系为,由此可知小明此次投掷的成绩是 m.
6.如图,正方形的边长为2,点在边上运动(不与点、重合),,点在射线上,且,与相交于点,连接、、.则下列结论:①;②;③;④面积的最大值为,其中正确结论的序号为 .
二、单选题
7.将抛物线先向右平移3个单位长度,再向下平移2个单位长度得到的新抛物线解析式为( )
A. B.
C. D.
8.把二次函数y=x2﹣4x+3化成y=a(x+h)2+k的形式是( )
A.y=(x+2)2+1 B.y=(x+2)2+7
C.y=(x﹣2)2﹣1 D.y=(x+2)2﹣7
9.下列函数中,属于二次函数的是( )
A. B. C. D.
10.抛物线 的顶点坐标为( )
A. B. C. D.
11.将抛物线y=3x2向右平移3个单位,所得到的抛物线是( )
A.y=3x2+3 B.y=3(x-3)2
C.y=3x2-3 D.y=3(x+3)2
12.以x为自变量的二次函数y= x2-2(b-2)x+ b2-1的 图象不经过第三象限,则实数b的取值范围是( )
A.b≧ B.b≧1或b≦-1 C.b≧2 D.1≦ b≦2
13.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①a<0;②a-b+c<0;③b2-4ac>0;④2a+b>0,其中正确的是( )
A.①②③④ B.②③④ C.①②③ D.①②④
14.如图,一次函数与二次函数的图象相交于两点,则函数的图象可能是( )
A. B.
C. D.
15.对于抛物线y=(x﹣1)2+2,下列说法中正确的是( )
A.开口向下 B.顶点坐标是(1,2)
C.与y轴交点坐标为(0,2) D.与x轴有两个交点
16.抛物线与轴相交于、两点,其顶点为,将此抛物线在轴下方的部分沿轴翻折,其余部分保持不变,如图得到一个新的图象.现有直线与该新图象有四个交点,则的取值范围为( )
A. B.
C. D.
三、解答题
17.抛物线的顶点坐标为 ,且与y轴的交点为 ,求此抛物线的解析式.
18.如图,抛物线与x轴交于点A,B,与y轴交于点C.求的面积.
19.小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x是多少时,矩形场地面积S最大,最大面积是多少?
20.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点左侧,B点的坐标为(4,0),与y轴交于C(0,﹣4)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP'C,那么是否存在点P,使四边形POP'C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
四、计算题
21.已知:二次函数的图象经过点.
(1)求b的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
22.根据以下素材,探索完成任务.
如何设计打印图纸方案?
素材1 如图1,正方形是一张用于打印产品的示意图,它由三个区块(Ⅰ,Ⅱ,Ⅲ)构成.已知,点E,F分别在和上,且,设.
素材2 为了打印精准,拟在图2中的边上设置一排间距为1cm的定位坐标(B为坐标原点),计算机可根据点E的定位坐标精准打印出图案.
问题解决
任务1 确定关系 用x的代数式表示: 区域Ⅰ的面积=______;区域Ⅱ的面积=______.
任务2 拟定方案 为了美观,拟将区域Ⅲ分割为甲、乙两个三角形区域,并要求区域乙是含边的三角形,求所有方案中乙的面积或者函数表达式.
任务3 优化设计 经调查发现当且x为整数时,此时称E点为合格定位点.当区域乙的面积最小时,合格定位点E点为最佳定位点,求出最佳定位点E的坐标.
23.如图1,已知二次函数图象与轴交点为,其顶点为.
(1)求二次函数的表达式;
(2)直线与轴交于,现将线段上下移动,若线段与二次函数的图象有交点,求向上和向下平移的最大距离;
(3)若将(1)中二次函数图象平移,使其顶点与原点重合,然后将其图象绕点顺时针旋转,得到抛物线,如图2所示,直线与交于,两点,为上位于直线左侧一点,求面积最大值,及此时点的坐标.
答案解析部分
1.【答案】6
【知识点】二次函数图象上点的坐标特征
2.【答案】2
【知识点】二次函数的定义
3.【答案】(3,1)
【知识点】二次函数y=a(x-h)²+k的性质
4.【答案】2
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=ax²+bx+c的图象
5.【答案】9
【知识点】直接开平方法解一元二次方程;二次函数的实际应用-抛球问题
6.【答案】①②④
【知识点】二次函数的最值;三角形全等及其性质;勾股定理;正方形的性质
7.【答案】C
【知识点】二次函数图象的几何变换
8.【答案】C
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
9.【答案】A
【知识点】二次函数的定义
10.【答案】D
【知识点】二次函数y=a(x-h)²+k的图象
11.【答案】B
【知识点】二次函数图象的几何变换
12.【答案】C
【知识点】二次函数图象上点的坐标特征
13.【答案】C
【知识点】二次函数图象与系数的关系;二次函数y=ax²+bx+c的性质
14.【答案】A
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
15.【答案】B
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=a(x-h)²+k的图象
16.【答案】B
【知识点】一元二次方程根的判别式及应用;待定系数法求一次函数解析式;二次函数图象与坐标轴的交点问题
17.【答案】解:∵抛物线的顶点坐标为 ,
∴设抛物线解析式为 ,
把 代入得 ,
解得 ,
∴抛物线解析式为 .
【知识点】待定系数法求二次函数解析式
18.【答案】21
【知识点】二次函数图象与坐标轴的交点问题
19.【答案】(1)、S=x(30﹣x)(0<x<30);(2)、x=15时,S有最大值为225平方米.
【知识点】二次函数的实际应用-几何问题
20.【答案】(1);(2);(3)当x=2时,四边形ABPC的面积最大,此时P点的坐标为:(2,﹣6),四边形ABPC的面积的最大值为18.
【知识点】二次函数的最值;待定系数法求二次函数解析式;菱形的判定与性质
21.【答案】(1)
(2),
【知识点】待定系数法求二次函数解析式;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
22.【答案】任务一:区块Ⅰ的面积:,区块Ⅱ的面积:;任务二:或;任务三:
【知识点】二次函数的实际应用-几何问题
23.【答案】(1)
(2)CM向下平移的最大距离为,向上平移的最大距离为6.
(3)
【知识点】待定系数法求二次函数解析式;旋转的性质
21世纪教育网(www.21cnjy.com)
2 / 7
