2.7正多边形与圆 同步练习(含答案)
文档属性
| 名称 | 2.7正多边形与圆 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 163.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 06:48:48 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2.7正多边形与圆
一、填空题
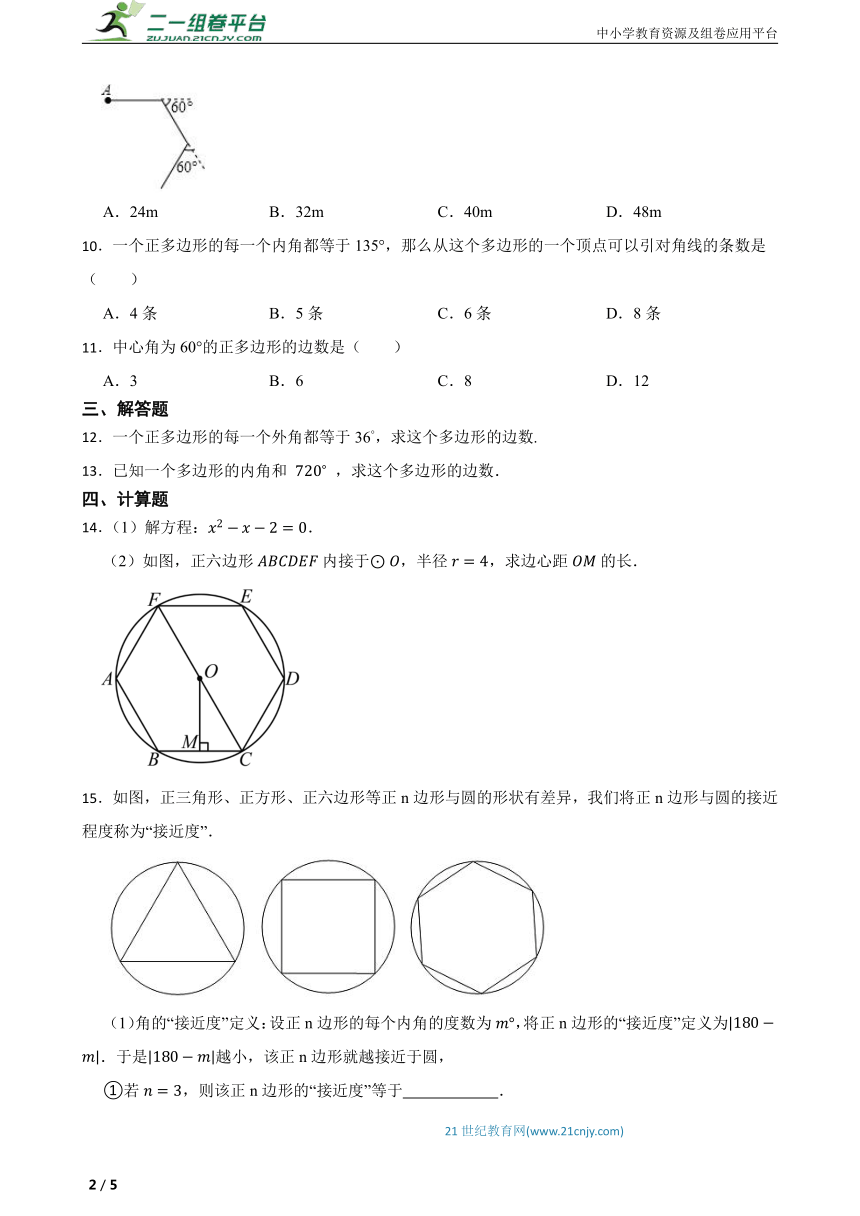
1.如图,正五边形内接于,点在上,则的度数为 .
2.正八边形的中心角为 度.
3.正多边形的一个中心角为36度,那么这个正多边形的一个内角等于 度.
4.若正六边形的边长是4,则其半径是 ,边心距是 ,面积是
5.若一个正多边形的每一个外角都等于36°,那么这个正多边形的中心角为 度.
6.如图,是等边的外接圆,若,则图中阴影部分的面积为 .(结果保留)
二、单选题
7.一个多边形的每个内角都等于135°,则这个多边形的边数为( )
A.8 B.9 C.10 D.11
8.如图,已知正五边形,,A、B、C、D、E均在上,连接,则的度数是( )
A. B. C. D.
9.如图,某人从点A出发,前进8m后向右转60°,再前进8m后又向右转60°,按照这样的方式一直走下去,当他第一次回到出发点A时,共走了( )
A.24m B.32m C.40m D.48m
10.一个正多边形的每一个内角都等于135°,那么从这个多边形的一个顶点可以引对角线的条数是( )
A.4条 B.5条 C.6条 D.8条
11.中心角为60°的正多边形的边数是( )
A.3 B.6 C.8 D.12
三、解答题
12.一个正多边形的每一个外角都等于36°,求这个多边形的边数.
13.已知一个多边形的内角和 ,求这个多边形的边数.
四、计算题
14.(1)解方程:.
(2)如图,正六边形内接于,半径,求边心距的长.
15.如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.
(1)角的“接近度”定义:设正n边形的每个内角的度数为,将正n边形的“接近度”定义为.于是越小,该正n边形就越接近于圆,
①若,则该正n边形的“接近度”等于 .
②若,则该正n边形的“接近度”等于______.
③当“接近度”等于______.时,正n边形就成了圆.
(2)边的“接近度”定义:设一个正n边形的外接圆的半径为R,正n边形的中心到各边的距离为d,将正n边形的“接近度”定义为.分别计算时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?
答案解析部分
1.【答案】36
【知识点】圆周角定理;圆内接正多边形
2.【答案】45°
【知识点】圆内接正多边形
3.【答案】144
【知识点】正多边形的性质
4.【答案】4;2 ;24
【知识点】圆内接正多边形
5.【答案】36
【知识点】正多边形的性质
6.【答案】
【知识点】圆内接正多边形
7.【答案】A
【知识点】正多边形的性质
8.【答案】A
【知识点】圆心角、弧、弦的关系;圆周角定理;圆内接正多边形
9.【答案】D
【知识点】正多边形的性质
10.【答案】B
【知识点】多边形的对角线;多边形内角与外角;正多边形的性质
11.【答案】B
【知识点】正多边形的性质
12.【答案】解:解:∵一个正多边形的每个外角都等于36°,
∴这个多边形的边数为360°÷36°=10.
【知识点】正多边形的性质
13.【答案】解:设这个多边形的边数是n,
依题意得 ,
,
.
答:这个多边形的边数是6.
【知识点】多边形内角与外角;正多边形的性质
14.【答案】(1), (2)
【知识点】公式法解一元二次方程;勾股定理;圆内接正多边形
15.【答案】(1)①120;②18;③0
(2)时,;时,,当边的“接近度”等于0时,正n边形就成了圆
【知识点】多边形内角与外角;圆内接正多边形
21世纪教育网(www.21cnjy.com)
5 / 5
2.7正多边形与圆
一、填空题
1.如图,正五边形内接于,点在上,则的度数为 .
2.正八边形的中心角为 度.
3.正多边形的一个中心角为36度,那么这个正多边形的一个内角等于 度.
4.若正六边形的边长是4,则其半径是 ,边心距是 ,面积是
5.若一个正多边形的每一个外角都等于36°,那么这个正多边形的中心角为 度.
6.如图,是等边的外接圆,若,则图中阴影部分的面积为 .(结果保留)
二、单选题
7.一个多边形的每个内角都等于135°,则这个多边形的边数为( )
A.8 B.9 C.10 D.11
8.如图,已知正五边形,,A、B、C、D、E均在上,连接,则的度数是( )
A. B. C. D.
9.如图,某人从点A出发,前进8m后向右转60°,再前进8m后又向右转60°,按照这样的方式一直走下去,当他第一次回到出发点A时,共走了( )
A.24m B.32m C.40m D.48m
10.一个正多边形的每一个内角都等于135°,那么从这个多边形的一个顶点可以引对角线的条数是( )
A.4条 B.5条 C.6条 D.8条
11.中心角为60°的正多边形的边数是( )
A.3 B.6 C.8 D.12
三、解答题
12.一个正多边形的每一个外角都等于36°,求这个多边形的边数.
13.已知一个多边形的内角和 ,求这个多边形的边数.
四、计算题
14.(1)解方程:.
(2)如图,正六边形内接于,半径,求边心距的长.
15.如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.
(1)角的“接近度”定义:设正n边形的每个内角的度数为,将正n边形的“接近度”定义为.于是越小,该正n边形就越接近于圆,
①若,则该正n边形的“接近度”等于 .
②若,则该正n边形的“接近度”等于______.
③当“接近度”等于______.时,正n边形就成了圆.
(2)边的“接近度”定义:设一个正n边形的外接圆的半径为R,正n边形的中心到各边的距离为d,将正n边形的“接近度”定义为.分别计算时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?
答案解析部分
1.【答案】36
【知识点】圆周角定理;圆内接正多边形
2.【答案】45°
【知识点】圆内接正多边形
3.【答案】144
【知识点】正多边形的性质
4.【答案】4;2 ;24
【知识点】圆内接正多边形
5.【答案】36
【知识点】正多边形的性质
6.【答案】
【知识点】圆内接正多边形
7.【答案】A
【知识点】正多边形的性质
8.【答案】A
【知识点】圆心角、弧、弦的关系;圆周角定理;圆内接正多边形
9.【答案】D
【知识点】正多边形的性质
10.【答案】B
【知识点】多边形的对角线;多边形内角与外角;正多边形的性质
11.【答案】B
【知识点】正多边形的性质
12.【答案】解:解:∵一个正多边形的每个外角都等于36°,
∴这个多边形的边数为360°÷36°=10.
【知识点】正多边形的性质
13.【答案】解:设这个多边形的边数是n,
依题意得 ,
,
.
答:这个多边形的边数是6.
【知识点】多边形内角与外角;正多边形的性质
14.【答案】(1), (2)
【知识点】公式法解一元二次方程;勾股定理;圆内接正多边形
15.【答案】(1)①120;②18;③0
(2)时,;时,,当边的“接近度”等于0时,正n边形就成了圆
【知识点】多边形内角与外角;圆内接正多边形
21世纪教育网(www.21cnjy.com)
5 / 5
