2024-2025学年第一学期甘肃省武威第二十七中学九年级数学人教版第二十四章《圆》练习卷(含答案)
文档属性
| 名称 | 2024-2025学年第一学期甘肃省武威第二十七中学九年级数学人教版第二十四章《圆》练习卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览



文档简介
2024-2025学年第一学期甘肃省武威市九年级
数学人教版第二十四章《圆》练习卷
一、单选题
1.如图,是的直径,弦,下列结论不一定成立的是( )
A. B.
C. D.
2.如图,点C、D在以为直径的半上,平分,于E,若,,则长为( )
A.2 B.3 C.4 D.5
3.如图,点A,B,C,D都在上,,若,则的度数为( )
A. B. C. D.
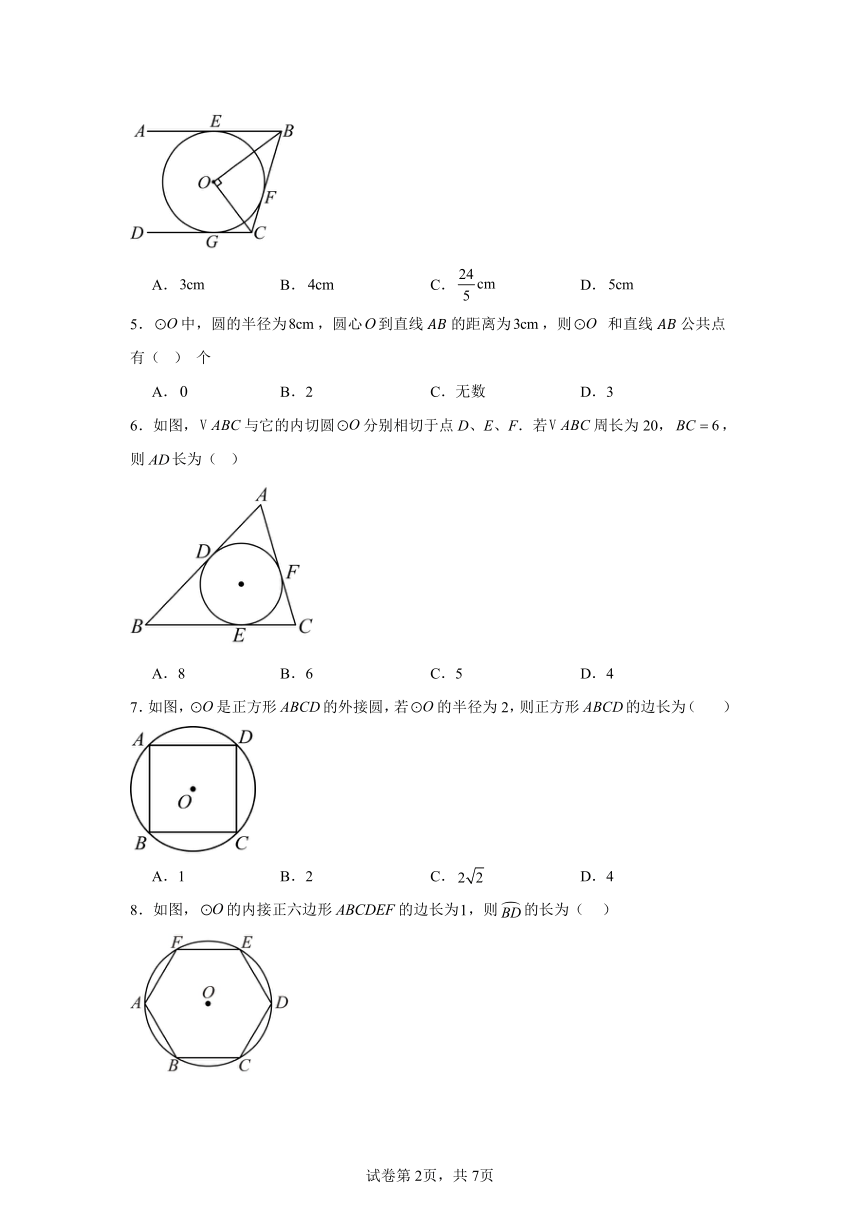
4.如图,直线、、分别与相切于点、、且,若,,则的半径等于( )
A. B. C. D.
5.中,圆的半径为,圆心到直线的距离为,则 和直线公共点有( ) 个
A. B.2 C.无数 D.3
6.如图,与它的内切圆分别相切于点D、E、F.若周长为20,,则长为( )
A.8 B.6 C.5 D.4
7.如图,是正方形的外接圆,若的半径为2,则正方形的边长为( )
A.1 B.2 C. D.4
8.如图,的内接正六边形的边长为,则的长为( )
A. B. C. D.
9.如图,在中,,则弧的长为( )
A. B. C. D.
10.已知内接于,.点A从圆周上某一点开始沿圆周运动,设点A运动的路线长为l,的面积为S,S随l变化的图象如图所示,其中.
①点A在运动的过程中,始终有;
②点M的纵坐标为;
③存在4个点A的位置,使得.
上述结论中,所有正确结论的序号是( )
A.② B.①③ C.②③ D.①②③
二、填空题
11.如图,的直径为,弦垂直平分半径,那么弦的长为 .
12.如图,在圆内接四边形中,,,若点,则圆的直径长为 .
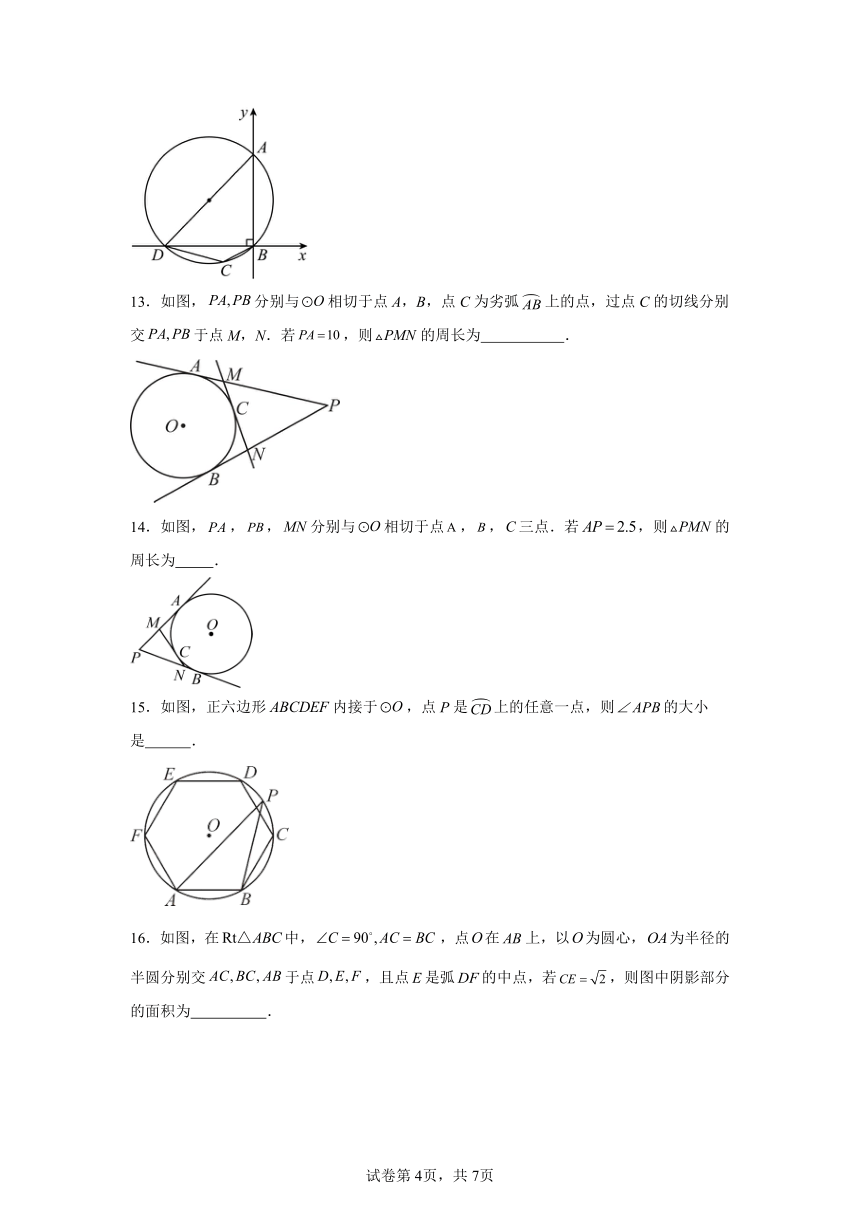
13.如图,分别与相切于点A,B,点C为劣弧上的点,过点C的切线分别交于点M,N.若,则的周长为 .
14.如图,,,分别与相切于点,,三点.若,则的周长为 .
15.如图,正六边形内接于,点P是上的任意一点,则的大小是 .
16.如图,在中,,点在上,以为圆心,为半径的半圆分别交于点,且点是弧的中点,若,则图中阴影部分的面积为 .
三、解答题
17.如图,已知为的弦,点H在上,请用尺规作图法在优弧上求作一点C,连接并延长交弦于点D,连接、,使得.(保留作图痕迹,不写作法)
18.如图,在中,,点,分别在,上,线段绕点D顺时针旋转得到,其中旋转角,此时点F恰好落在上,过点,,的圆交于点G,连接.
(1)若,求的度数;
(2)求证:.
19.如图,在四边形中,,的外接圆交于点E.
(1)若,求证:是的切线;
(2)若E是的中点,且,,求的长.
20.如图,在中,,以为直径的交于点D,E为的中点,连接并延长交的延长线于点F.
(1)求证:是的切线;
(2)若,,求长.
21.如图,的直径交于P,P是的中点.
(1)求的长;
(2)过点作,垂足为,求证:直线是的切线.
22.如图,的半径为r,六边形是圆的内接正六边形,四边形是正方形.
(1)求正六边形与正方形的面积比;
(2)连接,求度数.
23.如图,正八边形内接于,为弧上的一点(点不与点A,重合),求的度数.
24.如图,是的直径,C为延长线上一点,与相切于点E,连接,与交于点F,连接,且.
(1)求证:点F是的中点;
(2)若,的半径为3,则阴影部分的面积为____.
25.如图,为的外接圆,C是的中点,连接交于点D,延长至点E,使得平分.
(1)求证:直线是的切线.
(2)若的半径为5,,求的长.
(3)在(2)的前提下,点F在上,的内心G在边上,求的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C C C C B D C C A A
11.
12.
13.
14.5
15./30度
16.
17.解:如图,点即为所求.
根据作图可得
∵是线段的垂直平分线,
∴,
∴,
∴.
18.(1)解:∵,
∴,
∴;
(2)证明:连接,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
又∵,
∴,
∴,
∴.
19.(1)证明:如图,连接,,过点O作直线,
∵,,
∴直线是的垂直平分线,
∴直线,
∵,
∴,
∵是的半径,
∴是的切线;
(2)解:连接,交于点F,连接GC=GB,
∵E是的中点,
∴,,
∴,
在中,,,
∴,
在中,设,则,由勾股定理得,
,
即,
解得,
即半径为5,
∴,
在中,,,
∴,
∵,
∴,
解得.
20.(1)证明:如图,连接.
为的直径,
,
.
为中点,
.
.
,
.
,
,
,
,
,
为半径,
是的切线;
(2)解:,,
,
,
,
,
,
,
,
,
,
.
,
,
.
在中,,
,
,
,
,
.
21.(1)解:如图,连接,
是直径,
,
,
,
,
P是的中点,
;
(2)证明:如图,连接,
,P是的中点,
垂直平分,
,
,
,
,
,
,
,
,
又是半径,
直线是的切线.
22.(1)解:∵为正六边形的中心角,
∴.
∵,
∴是边长为r的等边三角形,
∴.
正方形的面积为,正六边形的面积为,
∴正六边形与正方形的面积比为;
(2)解:∵,
∴是等腰三角形.
∵,
∴,
∴.
23.解:如图,连接、、,
∵八边形是正八边形,
∴,
∴,
∴.
24.(1)证明:连接,设与相交于点H,
∵与相切于点E,
∴,
∴,,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴点F是的中点;
(2)∵,
∴,
∴,
∵,
∴,
由(1)可知,点F是的中点,
∴,
∴,
∴,
∵
∴,
∴阴影部分的面积为
故答案为:
【点睛】此题考查了切线的性质、含角直角三角形的性质、圆周角定理、垂径定理、等腰三角形的判定和性质等知识,证明点F是的中点是解题的关键.
25.(1)解:连接,
∵是的中点,
∴,
∴,
∵,
∴垂直平分,
∴,
∴,
∵,
∴,
∵,
∴,
∵平分,
∴,
∴
,
,
,
,
∴,
∴直线是的切线;
(2)解:∵垂直平分,
∴,,
∴,
∴,
∴;
(3)解:连接,
∵点为的内心,
∴,,
∴,
∴,
∵,,
∴,
∴.
答案第1页,共2页
答案第1页,共2页
数学人教版第二十四章《圆》练习卷
一、单选题
1.如图,是的直径,弦,下列结论不一定成立的是( )
A. B.
C. D.
2.如图,点C、D在以为直径的半上,平分,于E,若,,则长为( )
A.2 B.3 C.4 D.5
3.如图,点A,B,C,D都在上,,若,则的度数为( )
A. B. C. D.
4.如图,直线、、分别与相切于点、、且,若,,则的半径等于( )
A. B. C. D.
5.中,圆的半径为,圆心到直线的距离为,则 和直线公共点有( ) 个
A. B.2 C.无数 D.3
6.如图,与它的内切圆分别相切于点D、E、F.若周长为20,,则长为( )
A.8 B.6 C.5 D.4
7.如图,是正方形的外接圆,若的半径为2,则正方形的边长为( )
A.1 B.2 C. D.4
8.如图,的内接正六边形的边长为,则的长为( )
A. B. C. D.
9.如图,在中,,则弧的长为( )
A. B. C. D.
10.已知内接于,.点A从圆周上某一点开始沿圆周运动,设点A运动的路线长为l,的面积为S,S随l变化的图象如图所示,其中.
①点A在运动的过程中,始终有;
②点M的纵坐标为;
③存在4个点A的位置,使得.
上述结论中,所有正确结论的序号是( )
A.② B.①③ C.②③ D.①②③
二、填空题
11.如图,的直径为,弦垂直平分半径,那么弦的长为 .
12.如图,在圆内接四边形中,,,若点,则圆的直径长为 .
13.如图,分别与相切于点A,B,点C为劣弧上的点,过点C的切线分别交于点M,N.若,则的周长为 .
14.如图,,,分别与相切于点,,三点.若,则的周长为 .
15.如图,正六边形内接于,点P是上的任意一点,则的大小是 .
16.如图,在中,,点在上,以为圆心,为半径的半圆分别交于点,且点是弧的中点,若,则图中阴影部分的面积为 .
三、解答题
17.如图,已知为的弦,点H在上,请用尺规作图法在优弧上求作一点C,连接并延长交弦于点D,连接、,使得.(保留作图痕迹,不写作法)
18.如图,在中,,点,分别在,上,线段绕点D顺时针旋转得到,其中旋转角,此时点F恰好落在上,过点,,的圆交于点G,连接.
(1)若,求的度数;
(2)求证:.
19.如图,在四边形中,,的外接圆交于点E.
(1)若,求证:是的切线;
(2)若E是的中点,且,,求的长.
20.如图,在中,,以为直径的交于点D,E为的中点,连接并延长交的延长线于点F.
(1)求证:是的切线;
(2)若,,求长.
21.如图,的直径交于P,P是的中点.
(1)求的长;
(2)过点作,垂足为,求证:直线是的切线.
22.如图,的半径为r,六边形是圆的内接正六边形,四边形是正方形.
(1)求正六边形与正方形的面积比;
(2)连接,求度数.
23.如图,正八边形内接于,为弧上的一点(点不与点A,重合),求的度数.
24.如图,是的直径,C为延长线上一点,与相切于点E,连接,与交于点F,连接,且.
(1)求证:点F是的中点;
(2)若,的半径为3,则阴影部分的面积为____.
25.如图,为的外接圆,C是的中点,连接交于点D,延长至点E,使得平分.
(1)求证:直线是的切线.
(2)若的半径为5,,求的长.
(3)在(2)的前提下,点F在上,的内心G在边上,求的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C C C C B D C C A A
11.
12.
13.
14.5
15./30度
16.
17.解:如图,点即为所求.
根据作图可得
∵是线段的垂直平分线,
∴,
∴,
∴.
18.(1)解:∵,
∴,
∴;
(2)证明:连接,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
又∵,
∴,
∴,
∴.
19.(1)证明:如图,连接,,过点O作直线,
∵,,
∴直线是的垂直平分线,
∴直线,
∵,
∴,
∵是的半径,
∴是的切线;
(2)解:连接,交于点F,连接GC=GB,
∵E是的中点,
∴,,
∴,
在中,,,
∴,
在中,设,则,由勾股定理得,
,
即,
解得,
即半径为5,
∴,
在中,,,
∴,
∵,
∴,
解得.
20.(1)证明:如图,连接.
为的直径,
,
.
为中点,
.
.
,
.
,
,
,
,
,
为半径,
是的切线;
(2)解:,,
,
,
,
,
,
,
,
,
,
.
,
,
.
在中,,
,
,
,
,
.
21.(1)解:如图,连接,
是直径,
,
,
,
,
P是的中点,
;
(2)证明:如图,连接,
,P是的中点,
垂直平分,
,
,
,
,
,
,
,
,
又是半径,
直线是的切线.
22.(1)解:∵为正六边形的中心角,
∴.
∵,
∴是边长为r的等边三角形,
∴.
正方形的面积为,正六边形的面积为,
∴正六边形与正方形的面积比为;
(2)解:∵,
∴是等腰三角形.
∵,
∴,
∴.
23.解:如图,连接、、,
∵八边形是正八边形,
∴,
∴,
∴.
24.(1)证明:连接,设与相交于点H,
∵与相切于点E,
∴,
∴,,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴点F是的中点;
(2)∵,
∴,
∴,
∵,
∴,
由(1)可知,点F是的中点,
∴,
∴,
∴,
∵
∴,
∴阴影部分的面积为
故答案为:
【点睛】此题考查了切线的性质、含角直角三角形的性质、圆周角定理、垂径定理、等腰三角形的判定和性质等知识,证明点F是的中点是解题的关键.
25.(1)解:连接,
∵是的中点,
∴,
∴,
∵,
∴垂直平分,
∴,
∴,
∵,
∴,
∵,
∴,
∵平分,
∴,
∴
,
,
,
,
∴,
∴直线是的切线;
(2)解:∵垂直平分,
∴,,
∴,
∴,
∴;
(3)解:连接,
∵点为的内心,
∴,,
∴,
∴,
∵,,
∴,
∴.
答案第1页,共2页
答案第1页,共2页
同课章节目录
