湘教版数学九年级上册·下册综合检测题(含答案)
文档属性
| 名称 | 湘教版数学九年级上册·下册综合检测题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 359.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
湘教版数学九年级上册·下册综合检测题
一、填空题
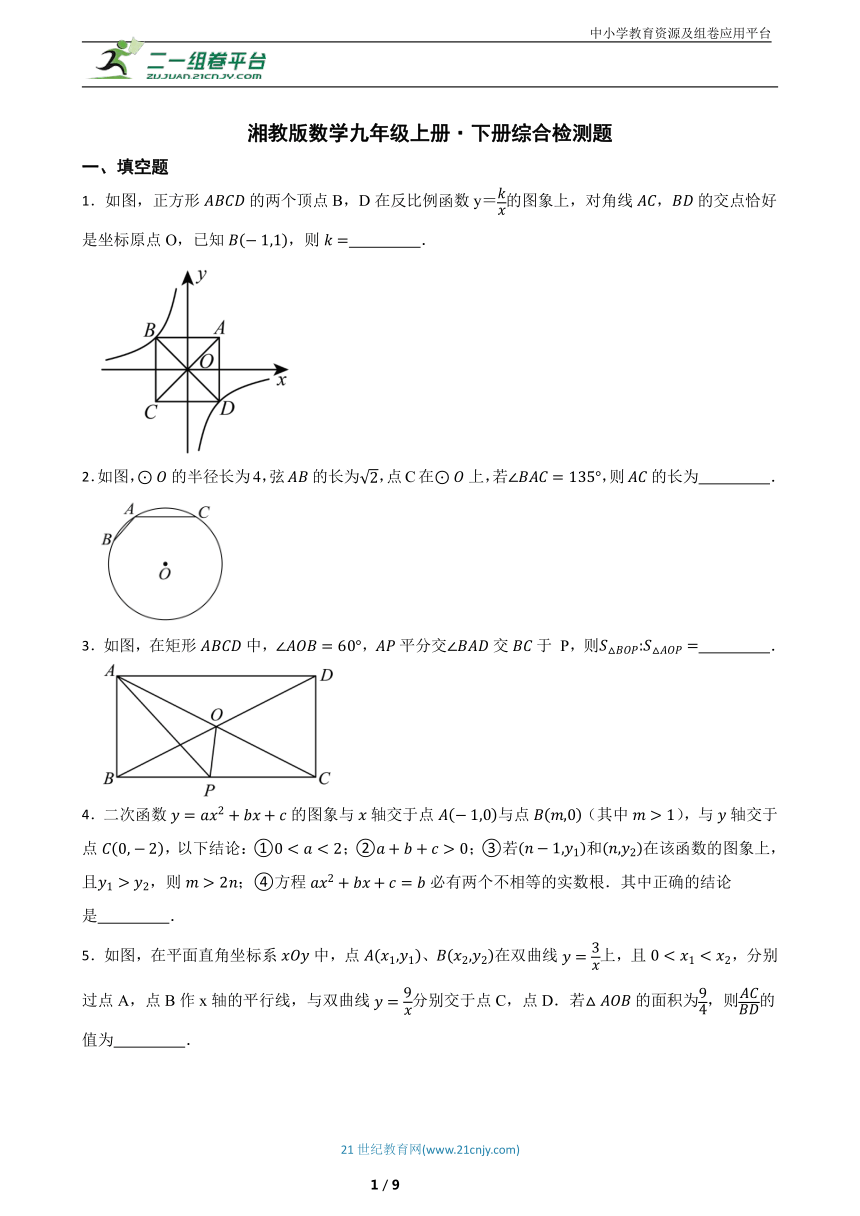
1.如图,正方形的两个顶点B,D在反比例函数y=的图象上,对角线,的交点恰好是坐标原点O,已知,则 .
2.如图,的半径长为4,弦的长为,点C在上,若,则的长为 .
3.如图,在矩形中,,平分交交于 P,则 .
4.二次函数的图象与轴交于点与点(其中),与轴交于点,以下结论:①;②;③若和在该函数的图象上,且,则;④方程必有两个不相等的实数根.其中正确的结论是 .
5.如图,在平面直角坐标系中,点、在双曲线上,且,分别过点A,点B作x轴的平行线,与双曲线分别交于点C,点D.若的面积为,则的值为 .
6.如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是 上一点.将扇形AOB沿EF对折,使得折叠后的圆弧 恰好与半径OB相切于点G.若OE=4,则O到折痕EF的距离为 .
二、单选题
7.若两个相似三角形的面积之比为,则它们的对应高线之比为( )
A. B. C. D.
8.如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF等于( )
A. B.1 C. D.2
9.将抛物线y= x2先向左平移5个单位,再向下平移4个单位,得到新抛物线的解析式是( )
A.y=-4 B.y=+4 C.y=-4 D.y=+4
10.反比例函数的图象经过、两点,则的值为( )
A. B. C. D.
11.体育老师对七(一)班学生1分钟内的跳绳次数进行了统计,发现最多的是125次,最少的是50次.现取组距为10绘制频数分布直方图,则此次调查的调查方式和适合的组数分别是( )
A.全面调查,8组 B.全面调查,7组
C.抽样调查,6组 D.全面调查,5组
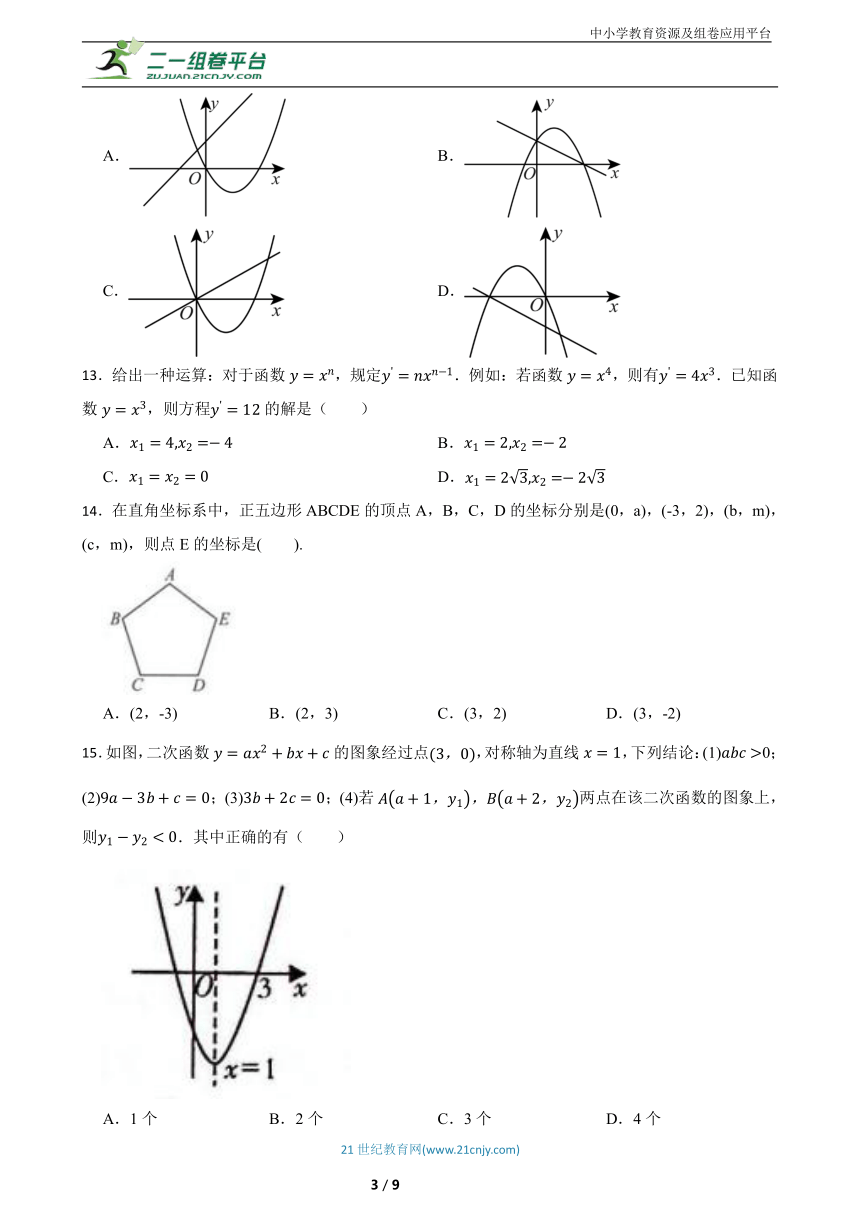
12.在同一平面直角坐标系中,画出直线与抛物线,这个图形可能是( )
A. B.
C. D.
13.给出一种运算:对于函数,规定.例如:若函数,则有.已知函数,则方程的解是( )
A. B.
C. D.
14.在直角坐标系中,正五边形ABCDE的顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( ).
A.(2,-3) B.(2,3) C.(3,2) D.(3,-2)
15.如图,二次函数的图象经过点,对称轴为直线,下列结论:(1)0;(2);(3);(4)若两点在该二次函数的图象上,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
16.如图,二次函数的图象经过点,且与轴交点的横坐标分别为,,其中,,顶点纵坐标大于.下列结论:;;;若,()是方程的两个根,则,.其中正确的结论有( )
A.个 B.个 C.个 D.个
三、解答题
17.如图,一次函数的图象与反比例函数图象相交于A、B两点,已知点B坐标为.
(1)求一次函数和反比例函数的解析式;
(2)观察图象,请直接写出不等式的解集.
18.已知关于的一元二次方程有两个不相等的实数根.
(1)求的取值范围;
(2)设方程的两个实数根分别为,若,求的值.
19.如图,矩形窗户边框由矩形,矩形,矩形组成,且.已知制作一个窗户边框的材料的总长是6米,设(米),窗户边框的面积为S().
(1)①用x的代数式表示;
②求x的取值范围.
(2)求当x取何值时,S达到最大,并求出最大值.
20.如图,、是的切线,切于点,的周长为12,.求:
(1)求的长;
(2)求的度数.
21.定义:若一元二次方程满足.则称此方程为“蚊龙”方程.
(1)当时,判断此时“蛟龙”方程解的情况,并说明理由.
(2)若“蛟龙”方程有两个相等的实数根,请解出此方程,
22.如图,E为正方形中边上的一个动点,,以为边画正方形与边交于点H.
(1)当E为边的中点时,求的长;
(2)当时,连接,求的长;
(3)连接,,求面积的最小值.
四、计算题
23.计算:
24.计算:
25.如图①,在中,,,,D为的中点,为的中位线,四边形为的内接矩形(矩形的四个顶点均在的边上).
(1)计算矩形的面积;
(2)将矩形沿向右平移、点F落在上时停止移动,在平移过程中,当矩形与重叠部分的面积为时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形,将矩形绕点按顺时针方向旋转,当H1落在上时停止转动,旋转后的矩形记为矩形,设旋转角为,求的值.
答案解析部分
1.【答案】
【知识点】待定系数法求反比例函数解析式
2.【答案】
【知识点】勾股定理;圆周角定理;圆内接四边形的性质
3.【答案】
【知识点】等腰三角形的判定;等边三角形的判定与性质;矩形的性质;解直角三角形
4.【答案】①③④
【知识点】二次函数图象与系数的关系;利用二次函数图象判断一元二次方程根的情况
5.【答案】
【知识点】因式分解法解一元二次方程;反比例函数系数k的几何意义
6.【答案】2
【知识点】切线的性质;翻折变换(折叠问题)
7.【答案】C
【知识点】相似三角形的性质
8.【答案】C
【知识点】相似三角形的判定与性质
9.【答案】A
【知识点】二次函数图象的几何变换
10.【答案】B
【知识点】反比例函数的概念;代入消元法解二元一次方程组
11.【答案】A
【知识点】全面调查与抽样调查;频数(率)分布直方图
12.【答案】D
【知识点】二次函数图象与系数的关系
13.【答案】B
【知识点】直接开平方法解一元二次方程
14.【答案】C
【知识点】关于坐标轴对称的点的坐标特征;正多边形的性质
15.【答案】B
【知识点】二次函数图象与系数的关系;二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
16.【答案】D
【知识点】二次函数图象与系数的关系
17.【答案】(1),
(2)或
【知识点】因式分解法解一元二次方程;反比例函数与一次函数的交点问题
18.【答案】(1)解:关于的一元二次方程有两个不相等的实数根,
,
解得.
(2)解:根据一元二次方程根与系数的关系可得,
,即
解得(不合题意,舍去),
【知识点】一元二次方程根的判别式及应用;一元二次方程的根与系数的关系(韦达定理)
19.【答案】(1)①②
(2)当时S有最大值,最大值为
【知识点】二次函数的实际应用-几何问题;代入消元法解二元一次方程组
20.【答案】(1)6
(2)
【知识点】切线的性质;切线长定理
21.【答案】(1)解:“蛟龙”方程有两个不相等的实数根,理由如下:
一元二次方程为“蛟龙”方程,
,
,
,
“蛟龙”方程有两个不相等的实数根;
(2)解:方程为“蛟龙”方程,
,
方程有两个相等的实数根,
,
或2,
当时,方程为,解得;
当时,方程为,解得.
故此方程的解为0或.
【知识点】一元二次方程根的判别式及应用
22.【答案】(1);
(2);
(3)的最小值为96.
【知识点】二次函数的最值;正方形的性质;相似三角形的判定与性质;解直角三角形
23.【答案】
【知识点】零指数幂;负整数指数幂;求特殊角的三角函数值
24.【答案】解:
.
【知识点】实数的运算;求特殊角的三角函数值
25.【答案】(1)
(2)
(3)
【知识点】解直角三角形;三角形的中位线定理;直角三角形斜边上的中线
21世纪教育网(www.21cnjy.com)
2 / 9
湘教版数学九年级上册·下册综合检测题
一、填空题
1.如图,正方形的两个顶点B,D在反比例函数y=的图象上,对角线,的交点恰好是坐标原点O,已知,则 .
2.如图,的半径长为4,弦的长为,点C在上,若,则的长为 .
3.如图,在矩形中,,平分交交于 P,则 .
4.二次函数的图象与轴交于点与点(其中),与轴交于点,以下结论:①;②;③若和在该函数的图象上,且,则;④方程必有两个不相等的实数根.其中正确的结论是 .
5.如图,在平面直角坐标系中,点、在双曲线上,且,分别过点A,点B作x轴的平行线,与双曲线分别交于点C,点D.若的面积为,则的值为 .
6.如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是 上一点.将扇形AOB沿EF对折,使得折叠后的圆弧 恰好与半径OB相切于点G.若OE=4,则O到折痕EF的距离为 .
二、单选题
7.若两个相似三角形的面积之比为,则它们的对应高线之比为( )
A. B. C. D.
8.如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF等于( )
A. B.1 C. D.2
9.将抛物线y= x2先向左平移5个单位,再向下平移4个单位,得到新抛物线的解析式是( )
A.y=-4 B.y=+4 C.y=-4 D.y=+4
10.反比例函数的图象经过、两点,则的值为( )
A. B. C. D.
11.体育老师对七(一)班学生1分钟内的跳绳次数进行了统计,发现最多的是125次,最少的是50次.现取组距为10绘制频数分布直方图,则此次调查的调查方式和适合的组数分别是( )
A.全面调查,8组 B.全面调查,7组
C.抽样调查,6组 D.全面调查,5组
12.在同一平面直角坐标系中,画出直线与抛物线,这个图形可能是( )
A. B.
C. D.
13.给出一种运算:对于函数,规定.例如:若函数,则有.已知函数,则方程的解是( )
A. B.
C. D.
14.在直角坐标系中,正五边形ABCDE的顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( ).
A.(2,-3) B.(2,3) C.(3,2) D.(3,-2)
15.如图,二次函数的图象经过点,对称轴为直线,下列结论:(1)0;(2);(3);(4)若两点在该二次函数的图象上,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
16.如图,二次函数的图象经过点,且与轴交点的横坐标分别为,,其中,,顶点纵坐标大于.下列结论:;;;若,()是方程的两个根,则,.其中正确的结论有( )
A.个 B.个 C.个 D.个
三、解答题
17.如图,一次函数的图象与反比例函数图象相交于A、B两点,已知点B坐标为.
(1)求一次函数和反比例函数的解析式;
(2)观察图象,请直接写出不等式的解集.
18.已知关于的一元二次方程有两个不相等的实数根.
(1)求的取值范围;
(2)设方程的两个实数根分别为,若,求的值.
19.如图,矩形窗户边框由矩形,矩形,矩形组成,且.已知制作一个窗户边框的材料的总长是6米,设(米),窗户边框的面积为S().
(1)①用x的代数式表示;
②求x的取值范围.
(2)求当x取何值时,S达到最大,并求出最大值.
20.如图,、是的切线,切于点,的周长为12,.求:
(1)求的长;
(2)求的度数.
21.定义:若一元二次方程满足.则称此方程为“蚊龙”方程.
(1)当时,判断此时“蛟龙”方程解的情况,并说明理由.
(2)若“蛟龙”方程有两个相等的实数根,请解出此方程,
22.如图,E为正方形中边上的一个动点,,以为边画正方形与边交于点H.
(1)当E为边的中点时,求的长;
(2)当时,连接,求的长;
(3)连接,,求面积的最小值.
四、计算题
23.计算:
24.计算:
25.如图①,在中,,,,D为的中点,为的中位线,四边形为的内接矩形(矩形的四个顶点均在的边上).
(1)计算矩形的面积;
(2)将矩形沿向右平移、点F落在上时停止移动,在平移过程中,当矩形与重叠部分的面积为时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形,将矩形绕点按顺时针方向旋转,当H1落在上时停止转动,旋转后的矩形记为矩形,设旋转角为,求的值.
答案解析部分
1.【答案】
【知识点】待定系数法求反比例函数解析式
2.【答案】
【知识点】勾股定理;圆周角定理;圆内接四边形的性质
3.【答案】
【知识点】等腰三角形的判定;等边三角形的判定与性质;矩形的性质;解直角三角形
4.【答案】①③④
【知识点】二次函数图象与系数的关系;利用二次函数图象判断一元二次方程根的情况
5.【答案】
【知识点】因式分解法解一元二次方程;反比例函数系数k的几何意义
6.【答案】2
【知识点】切线的性质;翻折变换(折叠问题)
7.【答案】C
【知识点】相似三角形的性质
8.【答案】C
【知识点】相似三角形的判定与性质
9.【答案】A
【知识点】二次函数图象的几何变换
10.【答案】B
【知识点】反比例函数的概念;代入消元法解二元一次方程组
11.【答案】A
【知识点】全面调查与抽样调查;频数(率)分布直方图
12.【答案】D
【知识点】二次函数图象与系数的关系
13.【答案】B
【知识点】直接开平方法解一元二次方程
14.【答案】C
【知识点】关于坐标轴对称的点的坐标特征;正多边形的性质
15.【答案】B
【知识点】二次函数图象与系数的关系;二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
16.【答案】D
【知识点】二次函数图象与系数的关系
17.【答案】(1),
(2)或
【知识点】因式分解法解一元二次方程;反比例函数与一次函数的交点问题
18.【答案】(1)解:关于的一元二次方程有两个不相等的实数根,
,
解得.
(2)解:根据一元二次方程根与系数的关系可得,
,即
解得(不合题意,舍去),
【知识点】一元二次方程根的判别式及应用;一元二次方程的根与系数的关系(韦达定理)
19.【答案】(1)①②
(2)当时S有最大值,最大值为
【知识点】二次函数的实际应用-几何问题;代入消元法解二元一次方程组
20.【答案】(1)6
(2)
【知识点】切线的性质;切线长定理
21.【答案】(1)解:“蛟龙”方程有两个不相等的实数根,理由如下:
一元二次方程为“蛟龙”方程,
,
,
,
“蛟龙”方程有两个不相等的实数根;
(2)解:方程为“蛟龙”方程,
,
方程有两个相等的实数根,
,
或2,
当时,方程为,解得;
当时,方程为,解得.
故此方程的解为0或.
【知识点】一元二次方程根的判别式及应用
22.【答案】(1);
(2);
(3)的最小值为96.
【知识点】二次函数的最值;正方形的性质;相似三角形的判定与性质;解直角三角形
23.【答案】
【知识点】零指数幂;负整数指数幂;求特殊角的三角函数值
24.【答案】解:
.
【知识点】实数的运算;求特殊角的三角函数值
25.【答案】(1)
(2)
(3)
【知识点】解直角三角形;三角形的中位线定理;直角三角形斜边上的中线
21世纪教育网(www.21cnjy.com)
2 / 9
同课章节目录
