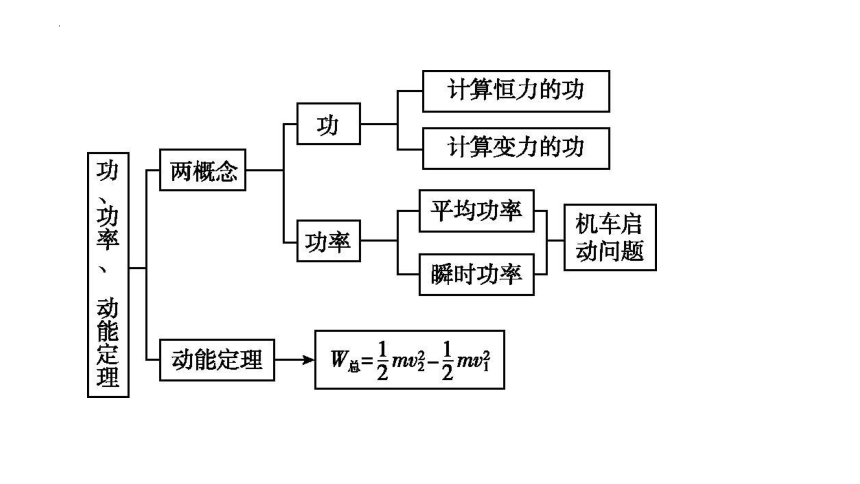
2025高考专题复习--动能定理及其应用 课件(共30张PPT)
文档属性
| 名称 | 2025高考专题复习--动能定理及其应用 课件(共30张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-03 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
案例1
例1.如图,用恒力F通过跨过光滑定滑轮的轻绳,将静止于水平面上的物体从位置A拉到位置B,物体和滑轮的大小均忽略,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,求绳的拉力F对物体做的功.
h
【分析】功是能量转化的量度,轻绳不存储能量,恒力F 做功通过绳子将能量转移到物体上,故此恒力F 做功应该等于绳子对物体做的功。
A
B
等效转化法
变式1:人在A点拉着绳通过一个光滑定滑轮以加速度a匀加速吊起质量为m的物体,如图所示,保持人手与滑轮间的距离不变,大小为h,开始时绳与水平方向成 600 角,当人拉着绳由A点沿水平方向运动到B点时,绳与水平方向成300 角,求人对绳的拉力做了多少功?(不计摩擦)
等效转化法
h
1.一质量为M的支架放在水平地面上,支架顶端用弹性绳拴着一
个小球,小球质量为m,弹性绳质量不计.将小球拉至水平位置,从静止开始释放,小球摆到最低点时,弹性绳的伸长量恰好达到最大,支架始终不动.不计空气阻力,重力加速度为g,以下说法正确的是( )
A.释放小球瞬间,支架对地面的压力大小为(m+M)g
B.小球摆到最低点时,支架对地面压力大于(m+M)g
C.小球摆到最低点的过程中,重力做功的功率一直在增大
D.小球摆到最低点的过程中,小球的重力势能可能全部转化为弹性绳的弹性势能
B
变式1 在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,电场强度大小E=6.0×105 N/C,方向与x轴正方向相同.在O处放一个电荷量q=-5.0×10-8 C、质量m=1.0×10-2 kg的绝缘物块.物块与水平面间的动摩擦因数μ=0.20,沿x轴正方向给物块一个初速度v0=2.0 m/s,如图所示.g取10 m/s2,求物块最终停止时的位置.
变式2 质量为m的小球在竖直向上的拉力作用下从静止
开始运动,其v-t图像如图所示(竖直向上为正方向,DE段为直线).已知重力加速度大小为g,下列说法正确的是( )
A.t3~t4时间内,小球竖直向下做匀减速直线运动
B.t0~t2时间内,合力对小球先做正功后做负功
C.0~t2时间内,小球的平均速度一定为
D.t3~t4时间内,拉力做的功为[(v4-v3)+g(t4-t3)]
D
考向1 应用动能定理求变力做功
A
考向2 在机车启动问题中应用动能定理
BD
02
应用动能定理处理多过程问题
PART ONE
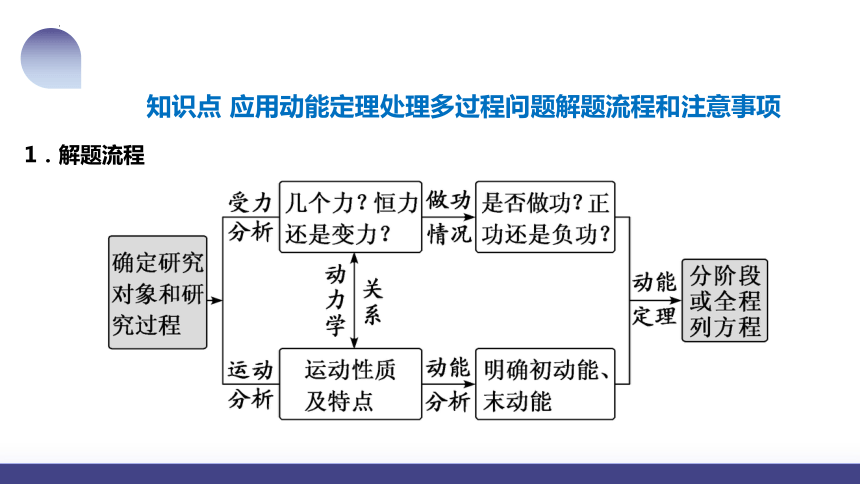
知识点 应用动能定理处理多过程问题解题流程和注意事项
1.解题流程
知识点 应用动能定理处理多过程问题解题流程和注意事项
2.注意事项
(1)动能定理中的位移和速度必须是相对于同一个参考系的,一般以地面或相对地面静止的物体为参考系。
(2)应用动能定理的关键在于对研究对象进行准确的受力分析及运动过程分析,并画出运动过程的草图,借助草图理解物理过程之间的关系。
(3)当物体的运动包含多个不同过程时,可分段应用动能定理求解;当所求解的问题不涉及中间的速度时,也可以全过程应用动能定理求解,这样更简便。
(4)列动能定理方程时,必须明确各力做功的正、负,确实难以判断的先假定为正功,最后根据结果加以检验。
考向1 多过程直线运动问题
D
考向2 直线曲线运动相结合的多过程问题
C
03
动能定理的图像问题
PART ONE
知识点1 四类图像所围“面积”的意义
知识点2 解决动能定理与图像问题的基本步骤
考向1 v-t图像
D
考向2 a-t图像
D
考向3 F-x图像
BC
考向4 P-t图像
D
真题感悟
提升·必备题型归纳
案例1
例1.如图,用恒力F通过跨过光滑定滑轮的轻绳,将静止于水平面上的物体从位置A拉到位置B,物体和滑轮的大小均忽略,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,求绳的拉力F对物体做的功.
h
【分析】功是能量转化的量度,轻绳不存储能量,恒力F 做功通过绳子将能量转移到物体上,故此恒力F 做功应该等于绳子对物体做的功。
A
B
等效转化法
变式1:人在A点拉着绳通过一个光滑定滑轮以加速度a匀加速吊起质量为m的物体,如图所示,保持人手与滑轮间的距离不变,大小为h,开始时绳与水平方向成 600 角,当人拉着绳由A点沿水平方向运动到B点时,绳与水平方向成300 角,求人对绳的拉力做了多少功?(不计摩擦)
等效转化法
h
1.一质量为M的支架放在水平地面上,支架顶端用弹性绳拴着一
个小球,小球质量为m,弹性绳质量不计.将小球拉至水平位置,从静止开始释放,小球摆到最低点时,弹性绳的伸长量恰好达到最大,支架始终不动.不计空气阻力,重力加速度为g,以下说法正确的是( )
A.释放小球瞬间,支架对地面的压力大小为(m+M)g
B.小球摆到最低点时,支架对地面压力大于(m+M)g
C.小球摆到最低点的过程中,重力做功的功率一直在增大
D.小球摆到最低点的过程中,小球的重力势能可能全部转化为弹性绳的弹性势能
B
变式1 在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,电场强度大小E=6.0×105 N/C,方向与x轴正方向相同.在O处放一个电荷量q=-5.0×10-8 C、质量m=1.0×10-2 kg的绝缘物块.物块与水平面间的动摩擦因数μ=0.20,沿x轴正方向给物块一个初速度v0=2.0 m/s,如图所示.g取10 m/s2,求物块最终停止时的位置.
变式2 质量为m的小球在竖直向上的拉力作用下从静止
开始运动,其v-t图像如图所示(竖直向上为正方向,DE段为直线).已知重力加速度大小为g,下列说法正确的是( )
A.t3~t4时间内,小球竖直向下做匀减速直线运动
B.t0~t2时间内,合力对小球先做正功后做负功
C.0~t2时间内,小球的平均速度一定为
D.t3~t4时间内,拉力做的功为[(v4-v3)+g(t4-t3)]
D
考向1 应用动能定理求变力做功
A
考向2 在机车启动问题中应用动能定理
BD
02
应用动能定理处理多过程问题
PART ONE
知识点 应用动能定理处理多过程问题解题流程和注意事项
1.解题流程
知识点 应用动能定理处理多过程问题解题流程和注意事项
2.注意事项
(1)动能定理中的位移和速度必须是相对于同一个参考系的,一般以地面或相对地面静止的物体为参考系。
(2)应用动能定理的关键在于对研究对象进行准确的受力分析及运动过程分析,并画出运动过程的草图,借助草图理解物理过程之间的关系。
(3)当物体的运动包含多个不同过程时,可分段应用动能定理求解;当所求解的问题不涉及中间的速度时,也可以全过程应用动能定理求解,这样更简便。
(4)列动能定理方程时,必须明确各力做功的正、负,确实难以判断的先假定为正功,最后根据结果加以检验。
考向1 多过程直线运动问题
D
考向2 直线曲线运动相结合的多过程问题
C
03
动能定理的图像问题
PART ONE
知识点1 四类图像所围“面积”的意义
知识点2 解决动能定理与图像问题的基本步骤
考向1 v-t图像
D
考向2 a-t图像
D
考向3 F-x图像
BC
考向4 P-t图像
D
真题感悟
提升·必备题型归纳
同课章节目录
