第七单元 扇形统计图 单元综合试题 小学数学人教版六年级上册
文档属性
| 名称 | 第七单元 扇形统计图 单元综合试题 小学数学人教版六年级上册 | 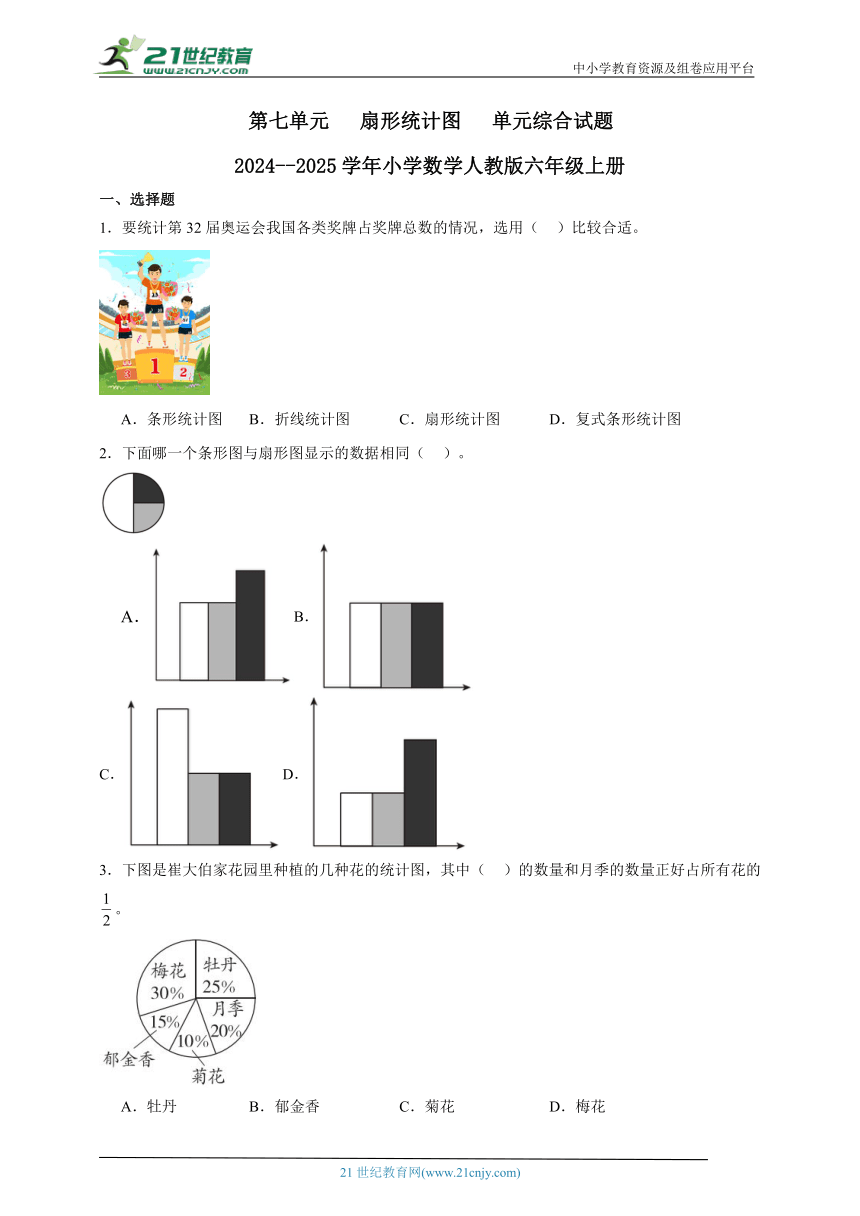 | |
| 格式 | docx | ||
| 文件大小 | 420.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 18:34:43 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
第七单元 扇形统计图 单元综合试题
2024--2025学年小学数学人教版六年级上册
一、选择题
1.要统计第32届奥运会我国各类奖牌占奖牌总数的情况,选用( )比较合适。
A.条形统计图 B.折线统计图 C.扇形统计图 D.复式条形统计图
2.下面哪一个条形图与扇形图显示的数据相同( )。
B.
C.D.
3.下图是崔大伯家花园里种植的几种花的统计图,其中( )的数量和月季的数量正好占所有花的。
A.牡丹 B.郁金香 C.菊花 D.梅花
4.实验小学对学生喜欢的球类进行调查,其中喜欢足球的有a人,其他情况如下图所示,那么喜欢乒乓球的人数可以表示为( )。
A.a×15% B.a÷15% C.a÷30% D.a÷30%×15%
5.野象群一路北上,引起民众的极大关注,为普及象群知识,需要绘制统计图。下面各话题,更适合用折线统计图表示的是( ),更适合用扇形统计图表示的是( )。
①几头成年野象睡眠时间长短比较
②野象在亚洲地区分布的百分比
③三十年来野象数量增减变化情况
④幼年和成年野象一天食量多少情况
A.①和③ B.①和④ C.③和② D.②和④
6.美国人口仅占全球人口的3.5%(约3亿人),但排放的二氧化碳却占全球排放量的24%以上,是世界最大的温室气体排放国。因此,近年来,碳中和的呼声越来越高,各国相应出台了碳中和政策。下列说法错误的是( )。
A.美国每一亿人口碳排放量占全球排放量的8%。
B.美国每一亿人口碳排放量比中国每一亿人口碳排放量多。
C.中国碳排放量是美国的
D.美国与欧盟的碳排放量之和比其他国家排放量之和(不包含中国)都多。
7.下图是某校五年级图书角各类图书数量统计情况。下面能比较准确地表达这一统计结果的是( )。
A. B. C. D.
8.扇形统计图表示( )。
A.数量的多少 B.部分和总量的关系 C.数量的增减变化 D.以上都可以
9.某种布料是由75%的棉和25%的氨纶组成的,下面( )统计图能正确表示这个信息。
A. B. C. D.
10.妈妈要统计小辉每次体育测试成绩,看看是进步还是退步,应绘制( )统计图。
A.条形 B.扇形 C.折线 D.扇形或者折线
二、填空题
11.如图是红旗小学参加全市“古诗词大赛”的获奖情况统计图。
(1)获得( )等奖的人数最多。
(2)获得优秀奖的人数占获奖总人数的( )%。
(3)根据统计,红旗小学获得优秀奖的有2人,照这样计算,红旗小学获奖的一共( )人,获得一等奖的有( )人。
(4)获得二等奖的人数比获得三等奖的人数少( )%。
12.《北京市生活垃圾管理条例》自2020年5月1日起正式开始实施。小刚收集并记录了自己家一周(7天)产生各类垃圾的质量,情况如下表。
种类 可回收垃圾 厨余垃圾 有害垃圾 其他垃圾
质量/kg 3.6 17.1 0.9 8.4
(1)下面图____________能代表小刚家这一周各类垃圾质量与垃圾总质量之间的关系。
A. B. C.
(2)小刚家这一周平均每天产生厨余垃圾 kg。(结果保留一位小数。)
(3)厨余垃圾经过特殊处理,能够转化成有机肥,转化后得到的有机肥质量约占厨余垃圾总量的20%。小刚家这一周产生的厨余垃圾大约能够转化成 kg的有机肥。
13.阅读材料后填一填。
材料一:2022年2月20日,第24届冬季奥林匹克运动会在北京落下帷幕。本届冬奥会,中国体育代表团在35个小项上实现参赛“零的突破”,最终获得9金4银2铜,金牌数和奖牌数均创历史新高,各项目获得奖牌情况如图。
材料二:在北京冬奥会自由式滑雪女子U型场地技巧决赛中,谷爱凌以95.25分的成绩获得金牌。
第24届冬奥会中国各项目获得奖牌情况统计图
(1)我国体育代表团在本届冬奥会获得的金牌数占奖牌总数的( )%。
(2)横线上的数读作( ),较高位上的“5”表示的数是另一个“5”表示的数的( )倍。
(3)在这届冬奥会中,中国健儿奋力拼搏,在多个项目创下历史最好成绩,尤其在( )项目表现最为突出,共获得( )枚奖牌。
三、判断题
14.实验小学六(3)班全体学生一次视力检查中,视力正常的人数、近视的人数和假性近视的人数分别占全班总人数的50%、30%、30%。( )
15.统计希望小学低年级和高年级同学最喜欢的课外读物情况,应该选择复式条形统计图。( )
16.体育老师想了解六年级(1)班学生喜欢每种运动项目的人数与全班人数之间的百分比关系,选用扇形统计图更合适。( )
17.要记录6月份30天内的气温变化情况,用条形统计图最合适。( )
18.张芳选用扇形统计图表示六年级各班人数的多少。( )
四、计算题
19.计算下列各题,能简便运算的要简便计算。
(1) (2)
20.解方程。
五、解答题
21.下面是六年级学生喜欢看的电视节目统计图。
(1)喜欢看《动物世界》的学生占六年级学生的( )%;喜欢看《今日说法》的学生占六年级学生的( )%。
(2)喜欢看( )的学生人数最多。
(3)如果六年级学生一共有200人,那么喜欢看《星光大道》的学生有多少人?
(4)如果喜欢看《探索·发现》的有90人,那么六年级学生一共有多少人?喜欢看《今日说法》的有多少人?
参考答案:
1.C
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系,据此解答。
因为扇形统计图反映部分与整体的关系,所以能明显看出第32届奥运会我国各类奖牌占奖牌总数的情况,因此选用扇形统计图比较合适。
2.C
观察扇形图,白色部分占了圆形面积的一半,深灰与浅灰部分相同且都为白色部分的一半,条形图也应该显示同样信息。
A.白色部分等于浅灰部分,排除;
B.三个部分数量相同,排除;
C.深灰与浅灰相等且为白色部分的一半,满足;
D.白色部分等于浅灰部分,排除。
3.D
根据扇形统计图,月季占花的20%,哪种花的数量和月季的数量占花的,根据分数与百分数的互化,,即哪种花的数量和月季的数量占花的50%,已知月季占花的20%,求另一种花占多少用减法。
50%-20%=30%
梅花的数量和月季的数量正好占所有花的。
4.D
根据题意,喜欢足球的有a人,占总人数的30%,那么总人数为(a÷30%)人;又已知喜欢乒乓球的人数占总人数的15%,用总人数×15%就可以算出喜欢乒乓球的人数。
由分析可得:喜欢乒乓球的人数可以表示为a÷30%×15%。
5.C
折线统计图能清楚地反映事物的变化情况;扇形统计图能清楚地表示出各部分在总体中所占的百分比;根据统计图的特点来判断,即可求解。
③中三十年来野象数量增减变化情况反映的是数量增减变化情况,因此更适合用折线统计图;
②中野象在亚洲地区分布的百分比表示的是各部分在总体中所占的百分比,因此应选用扇形统计图。
6.C
A.将二氧化碳全球排放量看作单位“1”,美国约3亿人,美国二氧化碳排放量对应百分率÷3=美国每一亿人口碳排放量占全球排放量的百分之几;
B.中国约14亿人,中国二氧化碳排放量对应百分率÷14=中国每一亿人口碳排放量占全球排放量的百分之几,与美国每一亿人口碳排放量占全球排放量的百分之几比较即可。
C.将美国碳排放量看作单位“1”,中国碳排放量对应百分率÷美国碳排放量对应百分率=中国碳排放量是美国的几分之几;
D.将美国的碳排放量对应百分率与欧盟的碳排放量对应百分率相加,与其他国家排放量对应百分率比较即可。
A.24%÷3=8%
美国每一亿人口碳排放量占全球排放量的8%,说法正确;
B.28%÷14=2%
8%>2%,美国每一亿人口碳排放量比中国每一亿人口碳排放量多,说法正确;
C.28%÷24%==
中国碳排放量是美国的,选项说法错误;
D.24%+13%=37%
37%>35%
美国与欧盟的碳排放量之和比其他国家排放量之和(不包含中国)都多,说法正确。
说法错误的是中国碳排放量是美国的。
7.B
从条形统计图中可知,故事类图书有80本,科技类图书有40本,作文类图书有30本,漫画类图书有10本,一共有(80+40+30+10)本,用各类图书的本数除以总本数,求出各类图书占总本数的百分比,也就是各类图书的扇形面积占整个圆面积的百分比,结合各选项中的扇形统计图得出结论。
图书总数:80+40+30+10=160(本)
故事类图书占总本数的:80÷160×100%=50%
科技类图书占总本数的:40÷160×100%=25%
作文类图书占总本数的:30÷160×100%=18.75%
漫画类图书占总本数的:10÷160×100%=6.25%
50%>25%>18.75%>6.25%
A.图中第二大扇形的面积占整个圆的百分比>25%,不符合题意;
B.图中最大扇形的面积占整个圆的50%,第二大扇形的面积占整个圆的25%,剩下的两个小扇形也有大小区分,所以这个扇形统计图能准确表达这一统计结果;
C.图中最大扇形的面积占整个圆的百分比<50%,第二大扇形的面积占整个圆的百分比>25%,不符合题意;
D.图中两个小的扇形面积一样大,不符合题意。
8.B
条形统计图能清楚地表示出数量的多少;
折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;
扇形统计图表示部分与整体之间的关系;据此解答。
根据分析可知,扇形统计图表示部分和总量的关系。
9.C
把布料的总成份看作单位“1”,根据扇形统计图的特征以及作用,用整个圆面积表示布料的总成分,其中棉占75%,氨纶占25%,据此选择即可。
A.,氨纶的百分比大于25%,不符合题意;
B.,氨纶的百分比比棉的大,不符合题意;
C.,棉占75%,氨纶占25%,符合题意;
D.,棉占25%,氨纶占75%,不符合题意。
某种布料是由75%的棉和25%的氨纶组成的,统计图能正确表示这个信息。
10.C
A.条形统计图主要用于比较不同类别之间的数据差异,不能直观地展示数据的变化趋势,所以不适合用来观察成绩的进步或退步情况。
B.扇形统计图主要用于展示各部分在总体中所占的比例关系,不适合用于体现成绩的变化。
C.折线统计图可以清晰地显示出小辉每次体育测试成绩的起伏变化,从而能直观地判断出是进步还是退步。例如,小辉第一次测试成绩是80分,第二次是85分,第三次是90分,通过折线统计图可以清楚地看到成绩呈上升趋势,表明在进步。
D.扇形统计图通常用于展示各部分所占的比例关系,比如在体育测试中各项成绩(如跑步、跳远、跳高)在总成绩中所占的比例。但对于单独观察每次测试成绩的变化趋势,扇形统计图无法直观呈现,所以不适合用于此情况。
折线统计图的特点是能清晰地反映数据的变化趋势。妈妈想要查看小辉每次体育测试成绩是进步还是退步,重点关注的是成绩的变化情况。
11.(1)三
(2)10
(3) 20 3
(4)50
(1)观察扇形统计图,哪个奖项所占的区域最大,那么获得这个奖项的人数就最多。
(2)把获奖总人数看作单位“1”,用“1”减去获得一等奖、二等奖、三等奖的人数分别占获奖总人数的百分比,即是获得优秀奖的人数占获奖总人数的百分之几。
(3)把获奖总人数看作单位“1”,已知获得优秀奖的有2人占获奖总人数的10%,单位“1”未知,用获得优秀奖的人数除以10%,即可求出获奖总人数;
从图中可知,获得一等奖的人数占获奖总人数的15%,根据求一个数的百分之几是多少,用获奖总人数乘15%,即是获得一等奖的人数。
(4)从图中可知,获得二等奖、三等奖的人数分别占获奖总人数的25%、50%,先用减法求出少的量,再除以获得三等奖占获奖总人数的百分比即可。
(1)获得三等奖的人数最多。
(2)1-15%-25%-50%=10%
获得优秀奖的人数占获奖总人数的10%。
(3)2÷10%
=2÷0.1
=20(人)
20×15%
=20×0.15
=3(人)
红旗小学获奖的一共20人,获得一等奖的有3人。
(4)(50%-25%)÷50%×100%
=(0.5-0.25)÷0.5×100%
=0.25÷0.5×100%
=0.5×100%
=50%
获得二等奖的人数比获得三等奖的人数少50%。
12.(1)C
(2)2.4
(3)3.42
(1)从统计表中可以看出,厨余垃圾最重,然后是其它垃圾、可回收垃圾、有害垃圾,据此选择合适的扇形统计图;
(2)从统计表看出,这一周产生了17.1kg厨余垃圾,一周有7天,求一周平均每天产生厨余垃圾的质量,用17.1除以7即可,注意结果保留一位小数;
(3)根据题意,转化后得到的有机肥质量约占厨余垃圾总量的20%,用厨余垃圾的质量乘20%,即可求出有机肥的转化量。
(1)
厨余垃圾>其他垃圾>可回收垃圾>有害垃圾
A.统计表中是4类垃圾,扇形统计图中只有3类,不符合题意;
B.扇形统计图中有害垃圾的扇形最大,不符合题意;
C.扇形统计图中各类垃圾的扇形大小符合各类垃圾的质量大小,符合题意。
故答案为:C
(2)(kg)
(3)(kg)
13.(1)60
(2) 九十五点二五 100
(3) 自由式滑雪 6
(1)把中国代表团获得的金、银、铜三种奖牌数量相加,可以得出中国代表团的奖牌总数,将奖牌总数看作单位“1”,根据百分数除法的意义,求一个数是另外一个数的百分之几用除法,即用金牌数量除以奖牌总数,可求出金牌数占奖牌总数的百分之几;
(2)根据小数的读法:整数部分按照整数的读法来读,小数点读作“点”,小数部分按顺序依次读出每一位上的数字。
小数的计数单位是十分之一、百分之一、千分之一……分别写作0.1、0.01、0.001…每相邻两个计数单位之间的进率是10。较高位上的“5”在个位上,表示5个1,即5,另一个“5”在百分位上,表示5个0.01,即0.05,求一个数是另外一个数是几倍,即用这个数除以另外一个数即可;
(3)通过对扇形统计图的观察,可得自由式滑雪获得的奖牌数量最多,将奖牌总数看作单位“1”,根据百分数乘法的意义,求一个数的百分之几是多少用乘法,即用奖牌总数乘40%即可。
(1)9+4+2=15(枚)
9÷15=0.6=60%
我国体育代表团在本届冬奥会获得的金牌数占奖牌总数的60%。
(2)95.25读作九十五点二五,5×1=5,5×0.01=0.05,5÷0.05=100,所以较高位上的“5”表示的数是另一个“5”表示的数的100倍。
(3)在这届冬奥会中,中国健儿奋力拼搏,在多个项目创下历史最好成绩,尤其在自由式滑雪项目表现最为突出,共获得奖牌数为:
15×40%=6(枚)
14.×
用百分数表示部分与总量之间的关系时,各个部分百分比的和应正好是100%。
50%+30%+30%
=80%+30%
=110%
不符合实际,故答案为×。
15.√
条形统计图可以清楚地看出数量的多少。
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
扇形统计图表示各部分数量与总数之间的关系。
统计希望小学低年级和高年级同学最喜欢的课外读物情况,应该选择复式条形统计图。
原题说法正确。
故答案为:√
16.√
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
由分析可得:想了解六年级(1)班学生喜欢每种运动项目的人数与全班人数之间的百分比关系,选用扇形统计图更合适,原题说法正确。
故答案为:√
17.×
条形统计图的特点:条形统计图能清楚地表示出每个项目的具体数目;折线统计图的特点:折线统计图不仅能表示数量的多少,还能清楚地反映数量的变化情况;扇形统计图的特点:扇形统计图能清楚地表示出各部分在总体中所占的百分比。
要记录6月份30天内的气温变化情况,用折线统计图最合适。原题干的说法是错误的。
故答案为:×
18.×
条形统计图能清楚地表示出数量的多少;
折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;
扇形统计图表示部分与整体之间的关系;据此解答。
根据分析可知,张芳选用条形统计图表示六年级各班人数的多少。
原题干说法错误。
故答案为:×
19.(1);(2)25
(1)根据运算顺序,先计算乘法,再计算加法,最后计算减法;
(2)根据除以一个数等于乘它的倒数,把式子转化为,再根据乘法分配律进行简算。
(1)
=
=
=
(2)
=
=(25+75)
=100
=25
20.;;
根据等式的性质解方程。
等式的性质1:等式两边同时加上或减去同一个数,等式仍然成立;
等式的性质2:等式两边同时乘或除以同一个不是零的数,等式仍然成立;
注意写“解”字和“=”要对齐。
解:
解:
解:
21.(1)24;26;
(2)《探索·发现》;
(3)40人;
(4)300人;
78人
(1)扇形统计图中六年级总人数看作单位“1”,喜欢《动物世界》的占24%,喜欢《星光大道》的占20%,喜欢《探索·发现》的占30%,剩下的是喜欢今日说法的。因此求喜欢今日说法的占六年级的百分之多少用减法。
(2)由每个节目占比可知,30%>26%>24%>20%,因此喜欢《探索·发现》的人最多。
(3)六年级人数是200人,喜欢《星光大道》的占20%,求喜欢《星光大道》有多少人用乘法。
(4)喜欢看《探索·发现》的有90人,占六年级人数的30%,已知六年级人数的百分之几是多少,求六年级人数数用除法。求喜欢看《今日说法》的人数,用六年级总人数乘喜欢看《今日说法》占六年级人数的百分之几。
(1)喜欢看《动物世界》的学生占六年级学生的24%;
1-24%-20%-30%
=76%-20%-30%
=56%-30%
=26%
喜欢看《今日说法》的学生占六年级学生的26%;
(2)喜欢看《探索·发现》的学生人数最多;
(3)200×20%=40(人)
如果六年级学生一共有200人,那么喜欢看《星光大道》的学生有40人;
(4)90÷30%=300(人)
300×26%=78(人)
如果喜欢看《探索·发现》的有90人,那么六年级学生一共有300人,喜欢看《今日说法》的有78人。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七单元 扇形统计图 单元综合试题
2024--2025学年小学数学人教版六年级上册
一、选择题
1.要统计第32届奥运会我国各类奖牌占奖牌总数的情况,选用( )比较合适。
A.条形统计图 B.折线统计图 C.扇形统计图 D.复式条形统计图
2.下面哪一个条形图与扇形图显示的数据相同( )。
B.
C.D.
3.下图是崔大伯家花园里种植的几种花的统计图,其中( )的数量和月季的数量正好占所有花的。
A.牡丹 B.郁金香 C.菊花 D.梅花
4.实验小学对学生喜欢的球类进行调查,其中喜欢足球的有a人,其他情况如下图所示,那么喜欢乒乓球的人数可以表示为( )。
A.a×15% B.a÷15% C.a÷30% D.a÷30%×15%
5.野象群一路北上,引起民众的极大关注,为普及象群知识,需要绘制统计图。下面各话题,更适合用折线统计图表示的是( ),更适合用扇形统计图表示的是( )。
①几头成年野象睡眠时间长短比较
②野象在亚洲地区分布的百分比
③三十年来野象数量增减变化情况
④幼年和成年野象一天食量多少情况
A.①和③ B.①和④ C.③和② D.②和④
6.美国人口仅占全球人口的3.5%(约3亿人),但排放的二氧化碳却占全球排放量的24%以上,是世界最大的温室气体排放国。因此,近年来,碳中和的呼声越来越高,各国相应出台了碳中和政策。下列说法错误的是( )。
A.美国每一亿人口碳排放量占全球排放量的8%。
B.美国每一亿人口碳排放量比中国每一亿人口碳排放量多。
C.中国碳排放量是美国的
D.美国与欧盟的碳排放量之和比其他国家排放量之和(不包含中国)都多。
7.下图是某校五年级图书角各类图书数量统计情况。下面能比较准确地表达这一统计结果的是( )。
A. B. C. D.
8.扇形统计图表示( )。
A.数量的多少 B.部分和总量的关系 C.数量的增减变化 D.以上都可以
9.某种布料是由75%的棉和25%的氨纶组成的,下面( )统计图能正确表示这个信息。
A. B. C. D.
10.妈妈要统计小辉每次体育测试成绩,看看是进步还是退步,应绘制( )统计图。
A.条形 B.扇形 C.折线 D.扇形或者折线
二、填空题
11.如图是红旗小学参加全市“古诗词大赛”的获奖情况统计图。
(1)获得( )等奖的人数最多。
(2)获得优秀奖的人数占获奖总人数的( )%。
(3)根据统计,红旗小学获得优秀奖的有2人,照这样计算,红旗小学获奖的一共( )人,获得一等奖的有( )人。
(4)获得二等奖的人数比获得三等奖的人数少( )%。
12.《北京市生活垃圾管理条例》自2020年5月1日起正式开始实施。小刚收集并记录了自己家一周(7天)产生各类垃圾的质量,情况如下表。
种类 可回收垃圾 厨余垃圾 有害垃圾 其他垃圾
质量/kg 3.6 17.1 0.9 8.4
(1)下面图____________能代表小刚家这一周各类垃圾质量与垃圾总质量之间的关系。
A. B. C.
(2)小刚家这一周平均每天产生厨余垃圾 kg。(结果保留一位小数。)
(3)厨余垃圾经过特殊处理,能够转化成有机肥,转化后得到的有机肥质量约占厨余垃圾总量的20%。小刚家这一周产生的厨余垃圾大约能够转化成 kg的有机肥。
13.阅读材料后填一填。
材料一:2022年2月20日,第24届冬季奥林匹克运动会在北京落下帷幕。本届冬奥会,中国体育代表团在35个小项上实现参赛“零的突破”,最终获得9金4银2铜,金牌数和奖牌数均创历史新高,各项目获得奖牌情况如图。
材料二:在北京冬奥会自由式滑雪女子U型场地技巧决赛中,谷爱凌以95.25分的成绩获得金牌。
第24届冬奥会中国各项目获得奖牌情况统计图
(1)我国体育代表团在本届冬奥会获得的金牌数占奖牌总数的( )%。
(2)横线上的数读作( ),较高位上的“5”表示的数是另一个“5”表示的数的( )倍。
(3)在这届冬奥会中,中国健儿奋力拼搏,在多个项目创下历史最好成绩,尤其在( )项目表现最为突出,共获得( )枚奖牌。
三、判断题
14.实验小学六(3)班全体学生一次视力检查中,视力正常的人数、近视的人数和假性近视的人数分别占全班总人数的50%、30%、30%。( )
15.统计希望小学低年级和高年级同学最喜欢的课外读物情况,应该选择复式条形统计图。( )
16.体育老师想了解六年级(1)班学生喜欢每种运动项目的人数与全班人数之间的百分比关系,选用扇形统计图更合适。( )
17.要记录6月份30天内的气温变化情况,用条形统计图最合适。( )
18.张芳选用扇形统计图表示六年级各班人数的多少。( )
四、计算题
19.计算下列各题,能简便运算的要简便计算。
(1) (2)
20.解方程。
五、解答题
21.下面是六年级学生喜欢看的电视节目统计图。
(1)喜欢看《动物世界》的学生占六年级学生的( )%;喜欢看《今日说法》的学生占六年级学生的( )%。
(2)喜欢看( )的学生人数最多。
(3)如果六年级学生一共有200人,那么喜欢看《星光大道》的学生有多少人?
(4)如果喜欢看《探索·发现》的有90人,那么六年级学生一共有多少人?喜欢看《今日说法》的有多少人?
参考答案:
1.C
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系,据此解答。
因为扇形统计图反映部分与整体的关系,所以能明显看出第32届奥运会我国各类奖牌占奖牌总数的情况,因此选用扇形统计图比较合适。
2.C
观察扇形图,白色部分占了圆形面积的一半,深灰与浅灰部分相同且都为白色部分的一半,条形图也应该显示同样信息。
A.白色部分等于浅灰部分,排除;
B.三个部分数量相同,排除;
C.深灰与浅灰相等且为白色部分的一半,满足;
D.白色部分等于浅灰部分,排除。
3.D
根据扇形统计图,月季占花的20%,哪种花的数量和月季的数量占花的,根据分数与百分数的互化,,即哪种花的数量和月季的数量占花的50%,已知月季占花的20%,求另一种花占多少用减法。
50%-20%=30%
梅花的数量和月季的数量正好占所有花的。
4.D
根据题意,喜欢足球的有a人,占总人数的30%,那么总人数为(a÷30%)人;又已知喜欢乒乓球的人数占总人数的15%,用总人数×15%就可以算出喜欢乒乓球的人数。
由分析可得:喜欢乒乓球的人数可以表示为a÷30%×15%。
5.C
折线统计图能清楚地反映事物的变化情况;扇形统计图能清楚地表示出各部分在总体中所占的百分比;根据统计图的特点来判断,即可求解。
③中三十年来野象数量增减变化情况反映的是数量增减变化情况,因此更适合用折线统计图;
②中野象在亚洲地区分布的百分比表示的是各部分在总体中所占的百分比,因此应选用扇形统计图。
6.C
A.将二氧化碳全球排放量看作单位“1”,美国约3亿人,美国二氧化碳排放量对应百分率÷3=美国每一亿人口碳排放量占全球排放量的百分之几;
B.中国约14亿人,中国二氧化碳排放量对应百分率÷14=中国每一亿人口碳排放量占全球排放量的百分之几,与美国每一亿人口碳排放量占全球排放量的百分之几比较即可。
C.将美国碳排放量看作单位“1”,中国碳排放量对应百分率÷美国碳排放量对应百分率=中国碳排放量是美国的几分之几;
D.将美国的碳排放量对应百分率与欧盟的碳排放量对应百分率相加,与其他国家排放量对应百分率比较即可。
A.24%÷3=8%
美国每一亿人口碳排放量占全球排放量的8%,说法正确;
B.28%÷14=2%
8%>2%,美国每一亿人口碳排放量比中国每一亿人口碳排放量多,说法正确;
C.28%÷24%==
中国碳排放量是美国的,选项说法错误;
D.24%+13%=37%
37%>35%
美国与欧盟的碳排放量之和比其他国家排放量之和(不包含中国)都多,说法正确。
说法错误的是中国碳排放量是美国的。
7.B
从条形统计图中可知,故事类图书有80本,科技类图书有40本,作文类图书有30本,漫画类图书有10本,一共有(80+40+30+10)本,用各类图书的本数除以总本数,求出各类图书占总本数的百分比,也就是各类图书的扇形面积占整个圆面积的百分比,结合各选项中的扇形统计图得出结论。
图书总数:80+40+30+10=160(本)
故事类图书占总本数的:80÷160×100%=50%
科技类图书占总本数的:40÷160×100%=25%
作文类图书占总本数的:30÷160×100%=18.75%
漫画类图书占总本数的:10÷160×100%=6.25%
50%>25%>18.75%>6.25%
A.图中第二大扇形的面积占整个圆的百分比>25%,不符合题意;
B.图中最大扇形的面积占整个圆的50%,第二大扇形的面积占整个圆的25%,剩下的两个小扇形也有大小区分,所以这个扇形统计图能准确表达这一统计结果;
C.图中最大扇形的面积占整个圆的百分比<50%,第二大扇形的面积占整个圆的百分比>25%,不符合题意;
D.图中两个小的扇形面积一样大,不符合题意。
8.B
条形统计图能清楚地表示出数量的多少;
折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;
扇形统计图表示部分与整体之间的关系;据此解答。
根据分析可知,扇形统计图表示部分和总量的关系。
9.C
把布料的总成份看作单位“1”,根据扇形统计图的特征以及作用,用整个圆面积表示布料的总成分,其中棉占75%,氨纶占25%,据此选择即可。
A.,氨纶的百分比大于25%,不符合题意;
B.,氨纶的百分比比棉的大,不符合题意;
C.,棉占75%,氨纶占25%,符合题意;
D.,棉占25%,氨纶占75%,不符合题意。
某种布料是由75%的棉和25%的氨纶组成的,统计图能正确表示这个信息。
10.C
A.条形统计图主要用于比较不同类别之间的数据差异,不能直观地展示数据的变化趋势,所以不适合用来观察成绩的进步或退步情况。
B.扇形统计图主要用于展示各部分在总体中所占的比例关系,不适合用于体现成绩的变化。
C.折线统计图可以清晰地显示出小辉每次体育测试成绩的起伏变化,从而能直观地判断出是进步还是退步。例如,小辉第一次测试成绩是80分,第二次是85分,第三次是90分,通过折线统计图可以清楚地看到成绩呈上升趋势,表明在进步。
D.扇形统计图通常用于展示各部分所占的比例关系,比如在体育测试中各项成绩(如跑步、跳远、跳高)在总成绩中所占的比例。但对于单独观察每次测试成绩的变化趋势,扇形统计图无法直观呈现,所以不适合用于此情况。
折线统计图的特点是能清晰地反映数据的变化趋势。妈妈想要查看小辉每次体育测试成绩是进步还是退步,重点关注的是成绩的变化情况。
11.(1)三
(2)10
(3) 20 3
(4)50
(1)观察扇形统计图,哪个奖项所占的区域最大,那么获得这个奖项的人数就最多。
(2)把获奖总人数看作单位“1”,用“1”减去获得一等奖、二等奖、三等奖的人数分别占获奖总人数的百分比,即是获得优秀奖的人数占获奖总人数的百分之几。
(3)把获奖总人数看作单位“1”,已知获得优秀奖的有2人占获奖总人数的10%,单位“1”未知,用获得优秀奖的人数除以10%,即可求出获奖总人数;
从图中可知,获得一等奖的人数占获奖总人数的15%,根据求一个数的百分之几是多少,用获奖总人数乘15%,即是获得一等奖的人数。
(4)从图中可知,获得二等奖、三等奖的人数分别占获奖总人数的25%、50%,先用减法求出少的量,再除以获得三等奖占获奖总人数的百分比即可。
(1)获得三等奖的人数最多。
(2)1-15%-25%-50%=10%
获得优秀奖的人数占获奖总人数的10%。
(3)2÷10%
=2÷0.1
=20(人)
20×15%
=20×0.15
=3(人)
红旗小学获奖的一共20人,获得一等奖的有3人。
(4)(50%-25%)÷50%×100%
=(0.5-0.25)÷0.5×100%
=0.25÷0.5×100%
=0.5×100%
=50%
获得二等奖的人数比获得三等奖的人数少50%。
12.(1)C
(2)2.4
(3)3.42
(1)从统计表中可以看出,厨余垃圾最重,然后是其它垃圾、可回收垃圾、有害垃圾,据此选择合适的扇形统计图;
(2)从统计表看出,这一周产生了17.1kg厨余垃圾,一周有7天,求一周平均每天产生厨余垃圾的质量,用17.1除以7即可,注意结果保留一位小数;
(3)根据题意,转化后得到的有机肥质量约占厨余垃圾总量的20%,用厨余垃圾的质量乘20%,即可求出有机肥的转化量。
(1)
厨余垃圾>其他垃圾>可回收垃圾>有害垃圾
A.统计表中是4类垃圾,扇形统计图中只有3类,不符合题意;
B.扇形统计图中有害垃圾的扇形最大,不符合题意;
C.扇形统计图中各类垃圾的扇形大小符合各类垃圾的质量大小,符合题意。
故答案为:C
(2)(kg)
(3)(kg)
13.(1)60
(2) 九十五点二五 100
(3) 自由式滑雪 6
(1)把中国代表团获得的金、银、铜三种奖牌数量相加,可以得出中国代表团的奖牌总数,将奖牌总数看作单位“1”,根据百分数除法的意义,求一个数是另外一个数的百分之几用除法,即用金牌数量除以奖牌总数,可求出金牌数占奖牌总数的百分之几;
(2)根据小数的读法:整数部分按照整数的读法来读,小数点读作“点”,小数部分按顺序依次读出每一位上的数字。
小数的计数单位是十分之一、百分之一、千分之一……分别写作0.1、0.01、0.001…每相邻两个计数单位之间的进率是10。较高位上的“5”在个位上,表示5个1,即5,另一个“5”在百分位上,表示5个0.01,即0.05,求一个数是另外一个数是几倍,即用这个数除以另外一个数即可;
(3)通过对扇形统计图的观察,可得自由式滑雪获得的奖牌数量最多,将奖牌总数看作单位“1”,根据百分数乘法的意义,求一个数的百分之几是多少用乘法,即用奖牌总数乘40%即可。
(1)9+4+2=15(枚)
9÷15=0.6=60%
我国体育代表团在本届冬奥会获得的金牌数占奖牌总数的60%。
(2)95.25读作九十五点二五,5×1=5,5×0.01=0.05,5÷0.05=100,所以较高位上的“5”表示的数是另一个“5”表示的数的100倍。
(3)在这届冬奥会中,中国健儿奋力拼搏,在多个项目创下历史最好成绩,尤其在自由式滑雪项目表现最为突出,共获得奖牌数为:
15×40%=6(枚)
14.×
用百分数表示部分与总量之间的关系时,各个部分百分比的和应正好是100%。
50%+30%+30%
=80%+30%
=110%
不符合实际,故答案为×。
15.√
条形统计图可以清楚地看出数量的多少。
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
扇形统计图表示各部分数量与总数之间的关系。
统计希望小学低年级和高年级同学最喜欢的课外读物情况,应该选择复式条形统计图。
原题说法正确。
故答案为:√
16.√
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
由分析可得:想了解六年级(1)班学生喜欢每种运动项目的人数与全班人数之间的百分比关系,选用扇形统计图更合适,原题说法正确。
故答案为:√
17.×
条形统计图的特点:条形统计图能清楚地表示出每个项目的具体数目;折线统计图的特点:折线统计图不仅能表示数量的多少,还能清楚地反映数量的变化情况;扇形统计图的特点:扇形统计图能清楚地表示出各部分在总体中所占的百分比。
要记录6月份30天内的气温变化情况,用折线统计图最合适。原题干的说法是错误的。
故答案为:×
18.×
条形统计图能清楚地表示出数量的多少;
折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;
扇形统计图表示部分与整体之间的关系;据此解答。
根据分析可知,张芳选用条形统计图表示六年级各班人数的多少。
原题干说法错误。
故答案为:×
19.(1);(2)25
(1)根据运算顺序,先计算乘法,再计算加法,最后计算减法;
(2)根据除以一个数等于乘它的倒数,把式子转化为,再根据乘法分配律进行简算。
(1)
=
=
=
(2)
=
=(25+75)
=100
=25
20.;;
根据等式的性质解方程。
等式的性质1:等式两边同时加上或减去同一个数,等式仍然成立;
等式的性质2:等式两边同时乘或除以同一个不是零的数,等式仍然成立;
注意写“解”字和“=”要对齐。
解:
解:
解:
21.(1)24;26;
(2)《探索·发现》;
(3)40人;
(4)300人;
78人
(1)扇形统计图中六年级总人数看作单位“1”,喜欢《动物世界》的占24%,喜欢《星光大道》的占20%,喜欢《探索·发现》的占30%,剩下的是喜欢今日说法的。因此求喜欢今日说法的占六年级的百分之多少用减法。
(2)由每个节目占比可知,30%>26%>24%>20%,因此喜欢《探索·发现》的人最多。
(3)六年级人数是200人,喜欢《星光大道》的占20%,求喜欢《星光大道》有多少人用乘法。
(4)喜欢看《探索·发现》的有90人,占六年级人数的30%,已知六年级人数的百分之几是多少,求六年级人数数用除法。求喜欢看《今日说法》的人数,用六年级总人数乘喜欢看《今日说法》占六年级人数的百分之几。
(1)喜欢看《动物世界》的学生占六年级学生的24%;
1-24%-20%-30%
=76%-20%-30%
=56%-30%
=26%
喜欢看《今日说法》的学生占六年级学生的26%;
(2)喜欢看《探索·发现》的学生人数最多;
(3)200×20%=40(人)
如果六年级学生一共有200人,那么喜欢看《星光大道》的学生有40人;
(4)90÷30%=300(人)
300×26%=78(人)
如果喜欢看《探索·发现》的有90人,那么六年级学生一共有300人,喜欢看《今日说法》的有78人。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
