人教版九年级上册24.1.4 圆周角 课件(共20张PPT)
文档属性
| 名称 | 人教版九年级上册24.1.4 圆周角 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 10:43:14 | ||
图片预览




文档简介
(共20张PPT)
24.1.4 圆周角
人教版九年级上册
第二十四章 圆
教学目标
1.理解圆周角的定义,了解与圆心角的关系,会在具体情景中辨别圆周角。
2.掌握圆周角定理及推论,并会运用这些知识进行简单的计算和证明;
3.学习中经理操作、观察、猜想、分析、交流、论证等数学活动,体验圆周角的、定理的探索。
重点:理解并掌握圆周角定理及推论。
难点:圆周角定理的证明。
新知导入
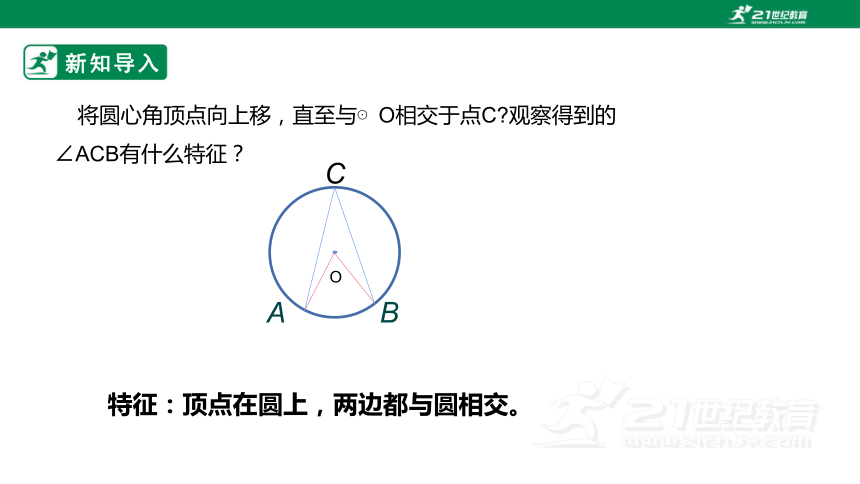
特征:顶点在圆上,两边都与圆相交。
将圆心角顶点向上移,直至与⊙O相交于点C 观察得到的∠ACB有什么特征?
O
A
C
B
新知讲解
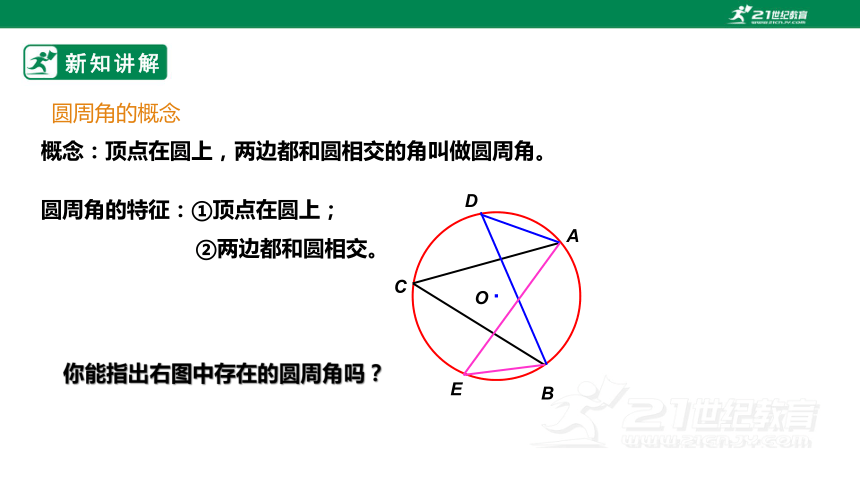
概念:顶点在圆上,两边都和圆相交的角叫做圆周角。
圆周角的特征:①顶点在圆上;
②两边都和圆相交。
·
A
B
C
D
E
O
你能指出右图中存在的圆周角吗?
圆周角的概念
新知讲解
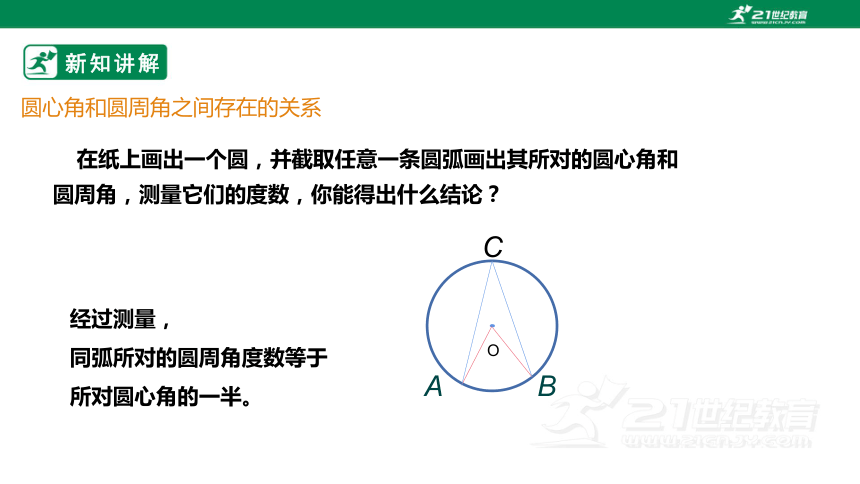
在纸上画出一个圆,并截取任意一条圆弧画出其所对的圆心角和圆周角,测量它们的度数,你能得出什么结论?
经过测量,
同弧所对的圆周角度数等于
所对圆心角的一半。
O
A
C
B
圆心角和圆周角之间存在的关系
新知讲解
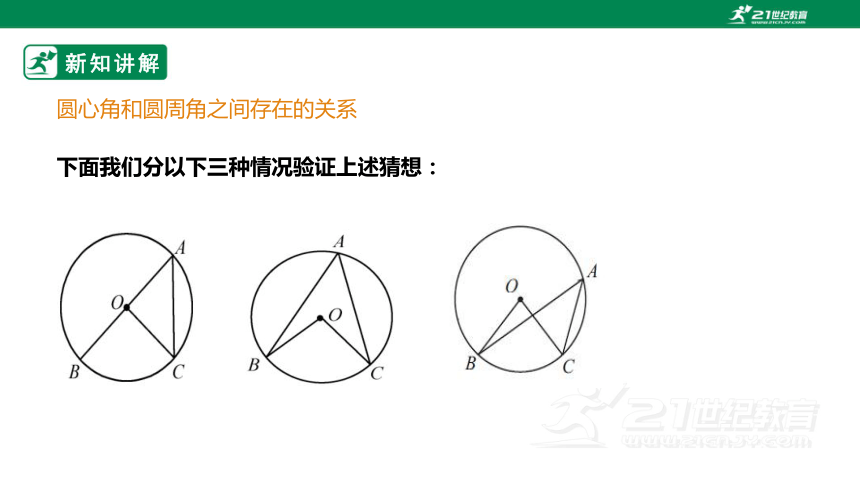
下面我们分以下三种情况验证上述猜想:
圆心角和圆周角之间存在的关系
新知讲解
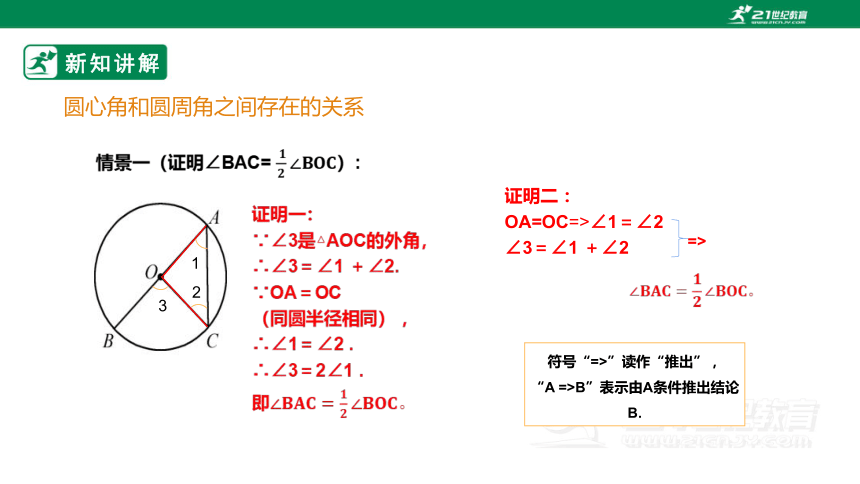
情景一(证明∠BAC= ):
1
2
3
证明一:
∵∠3是△AOC的外角,
∴∠3=∠1 +∠2.
∵OA=OC
(同圆半径相同) ,
∴∠1=∠2 .
∴∠3=2∠1 .
即
=>
证明二:
OA=OC=>∠1=∠2
∠3=∠1 +∠2
符号“=>”读作“推出”,
“A =>B”表示由A条件推出结论B.
圆心角和圆周角之间存在的关系
新知讲解
情景二(证明∠BAC= ):
1
2
3
4
5
6
证明:
∵∠5是△AOB的外角,∴∠5=∠1 +∠3.
∵OA=OB(同圆半径相同) ,
∴∠1=∠3 .∴∠5=2∠1
同理∠6=2∠2
=∠5+∠6= 2(∠1 +∠2)= 2
即
D
连接AO,延长AO,与⊙O相交于点D
圆心角和圆周角之间存在的关系
新知讲解
综上所述,圆周角∠BAC与圆心角∠BOC的大小关系是:
即 ∠BAC = ∠BOC.
一条弧所对的圆周角等于它所对的圆心角的一半。
圆心角和圆周角之间存在的关系
新知讲解
在同圆或等圆中,两条弧相等,则他们所对应的圆周角有什么关系?
·
O
A
B
B1
A1
将弧AB绕圆心O旋转,使弧AB与弧A1B1重合
∴点A与A1重合,B与B1重合
∴射线OB与OB1重合,射线OA与OA1重合
∴∠AOB=∠A1OB1
而一条弧所对的圆周角等于它所对的圆心角
的一半
∴它们所对应的的圆周角相同。
即同弧或等弧所对的圆周角相等。
C
圆心角和圆周角之间存在的关系
新知讲解
·
A
B
C1
O
C2
C3
证明:90°的圆周角所对的弦是直径?
圆心角和圆周角之间存在的关系
新知讲解
如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
解:∵AB是直径∴ ∠ACB= ∠ADB=90°
在Rt△ABC中,
∵CD平分∠ACB,
∴ AD=BD.
圆心角和圆周角之间存在的关系
新知讲解
O
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形。这个圆叫做这个多边形的外接圆。
例:四边形ABCD是⊙O的内接四边形, ⊙O是四边形ABCD的外接圆。
A
D
C
B
圆内接多边形概念
新知讲解
圆内接四边形的四个角之间有什么关系?
O
A
D
C
B
连接BO和DO
∠A所对的弧为BCD,∠C所对的弧为BAD
又∵ BCD和BAD所对圆心角的和为周角
∴ ∠A+ ∠C= ×360°=180°
即圆内接四边形的对角互补。
⌒
⌒
⌒
⌒
课堂练习
1、填空
1)如果∠A=45°,则∠BOC=____,∠OBC= 。
2)如果∠BOC=46°,则∠A=____。
3)如果BC的度数是46°,那么这条弧所对
的圆心角和圆周角分别等于 , 。
4)n°弧所对的圆心角是 ,所对的圆周角是 。
O
A
B
C
23°
46°
23°
n°
n°
90°
45°
⌒
课堂练习
2.如图,AB是⊙O的直径,C是⊙O上一点,OD是半径,且OD∥AC,
求证:CD=BD.
连接OC,
∵OD∥AC,
∴∠BOD=∠A,∠COD=∠C,
∵OA=OC,
∴∠A=∠C,
∴∠COD=∠BOD,
∴=.
课堂练习
3.如图,在半径为5 cm的⊙O中,AB为直径,∠ACD=30°,求弦BD的长.
由图得∠B=∠C=30°.
∵AB为直径,∴∠ADB=90°.
而AD=5∴BD=
课堂总结
概念:顶点在圆上,两边都和圆相交的角叫做圆周角。
圆周角的特征:①顶点在圆上;
②两边都和圆相交。
圆周角的概念
同弧所对的圆周角度数等于所对圆心角的一半。
90°的圆周角所对的弦是直径
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
24.1.4 圆周角
人教版九年级上册
第二十四章 圆
教学目标
1.理解圆周角的定义,了解与圆心角的关系,会在具体情景中辨别圆周角。
2.掌握圆周角定理及推论,并会运用这些知识进行简单的计算和证明;
3.学习中经理操作、观察、猜想、分析、交流、论证等数学活动,体验圆周角的、定理的探索。
重点:理解并掌握圆周角定理及推论。
难点:圆周角定理的证明。
新知导入
特征:顶点在圆上,两边都与圆相交。
将圆心角顶点向上移,直至与⊙O相交于点C 观察得到的∠ACB有什么特征?
O
A
C
B
新知讲解
概念:顶点在圆上,两边都和圆相交的角叫做圆周角。
圆周角的特征:①顶点在圆上;
②两边都和圆相交。
·
A
B
C
D
E
O
你能指出右图中存在的圆周角吗?
圆周角的概念
新知讲解
在纸上画出一个圆,并截取任意一条圆弧画出其所对的圆心角和圆周角,测量它们的度数,你能得出什么结论?
经过测量,
同弧所对的圆周角度数等于
所对圆心角的一半。
O
A
C
B
圆心角和圆周角之间存在的关系
新知讲解
下面我们分以下三种情况验证上述猜想:
圆心角和圆周角之间存在的关系
新知讲解
情景一(证明∠BAC= ):
1
2
3
证明一:
∵∠3是△AOC的外角,
∴∠3=∠1 +∠2.
∵OA=OC
(同圆半径相同) ,
∴∠1=∠2 .
∴∠3=2∠1 .
即
=>
证明二:
OA=OC=>∠1=∠2
∠3=∠1 +∠2
符号“=>”读作“推出”,
“A =>B”表示由A条件推出结论B.
圆心角和圆周角之间存在的关系
新知讲解
情景二(证明∠BAC= ):
1
2
3
4
5
6
证明:
∵∠5是△AOB的外角,∴∠5=∠1 +∠3.
∵OA=OB(同圆半径相同) ,
∴∠1=∠3 .∴∠5=2∠1
同理∠6=2∠2
=∠5+∠6= 2(∠1 +∠2)= 2
即
D
连接AO,延长AO,与⊙O相交于点D
圆心角和圆周角之间存在的关系
新知讲解
综上所述,圆周角∠BAC与圆心角∠BOC的大小关系是:
即 ∠BAC = ∠BOC.
一条弧所对的圆周角等于它所对的圆心角的一半。
圆心角和圆周角之间存在的关系
新知讲解
在同圆或等圆中,两条弧相等,则他们所对应的圆周角有什么关系?
·
O
A
B
B1
A1
将弧AB绕圆心O旋转,使弧AB与弧A1B1重合
∴点A与A1重合,B与B1重合
∴射线OB与OB1重合,射线OA与OA1重合
∴∠AOB=∠A1OB1
而一条弧所对的圆周角等于它所对的圆心角
的一半
∴它们所对应的的圆周角相同。
即同弧或等弧所对的圆周角相等。
C
圆心角和圆周角之间存在的关系
新知讲解
·
A
B
C1
O
C2
C3
证明:90°的圆周角所对的弦是直径?
圆心角和圆周角之间存在的关系
新知讲解
如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
解:∵AB是直径∴ ∠ACB= ∠ADB=90°
在Rt△ABC中,
∵CD平分∠ACB,
∴ AD=BD.
圆心角和圆周角之间存在的关系
新知讲解
O
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形。这个圆叫做这个多边形的外接圆。
例:四边形ABCD是⊙O的内接四边形, ⊙O是四边形ABCD的外接圆。
A
D
C
B
圆内接多边形概念
新知讲解
圆内接四边形的四个角之间有什么关系?
O
A
D
C
B
连接BO和DO
∠A所对的弧为BCD,∠C所对的弧为BAD
又∵ BCD和BAD所对圆心角的和为周角
∴ ∠A+ ∠C= ×360°=180°
即圆内接四边形的对角互补。
⌒
⌒
⌒
⌒
课堂练习
1、填空
1)如果∠A=45°,则∠BOC=____,∠OBC= 。
2)如果∠BOC=46°,则∠A=____。
3)如果BC的度数是46°,那么这条弧所对
的圆心角和圆周角分别等于 , 。
4)n°弧所对的圆心角是 ,所对的圆周角是 。
O
A
B
C
23°
46°
23°
n°
n°
90°
45°
⌒
课堂练习
2.如图,AB是⊙O的直径,C是⊙O上一点,OD是半径,且OD∥AC,
求证:CD=BD.
连接OC,
∵OD∥AC,
∴∠BOD=∠A,∠COD=∠C,
∵OA=OC,
∴∠A=∠C,
∴∠COD=∠BOD,
∴=.
课堂练习
3.如图,在半径为5 cm的⊙O中,AB为直径,∠ACD=30°,求弦BD的长.
由图得∠B=∠C=30°.
∵AB为直径,∴∠ADB=90°.
而AD=5∴BD=
课堂总结
概念:顶点在圆上,两边都和圆相交的角叫做圆周角。
圆周角的特征:①顶点在圆上;
②两边都和圆相交。
圆周角的概念
同弧所对的圆周角度数等于所对圆心角的一半。
90°的圆周角所对的弦是直径
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
