第2讲 整式与因式分解 2025年中考数学专题复习课件(共28张PPT)(湖南)
文档属性
| 名称 | 第2讲 整式与因式分解 2025年中考数学专题复习课件(共28张PPT)(湖南) |

|
|
| 格式 | pptx | ||
| 文件大小 | 637.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
第2讲 整式与因式分解
目录
CONTENTS
课标要求 作业目标
1
教材整合 核心归纳
2
重点精讲 变式探究
3
课标要求 作业目标
01
第一单元 第2讲
课标要求 作业目标
整式的加减 能分析具体问题中的简单数量关系,并用代数式表示,并会把具体数代入代数式求值.掌握单项式、多项式的相关概念,并能根据运算法则进行同类项的合并及相关的四则运算. 知道单项式的概念,会辨别单项式,能确定单项式的系数和次数
知道同类项的概念,能辨别几个单项式是否是同类项
掌握合并同类项的法则,会运用法则,并把单项式按某个字幕的升(降)幂排列
掌握去括号的规律,能运用规律进行整式的加减运算
掌握整式加减的运算法则,能运用法则进行整式的加减运算,并根据字母的值求整式的值
要求与目标
知道多项式和整式的概念,会辨别多项式和整式,能确定多项式的项数、次数和常数项
课标要求 作业目标
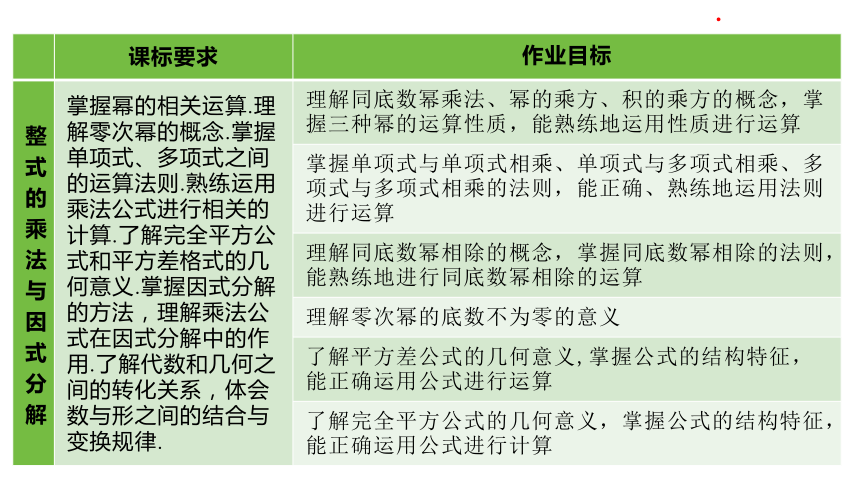
整式的乘法与因式分解 掌握幂的相关运算.理解零次幂的概念.掌握单项式、多项式之间的运算法则.熟练运用乘法公式进行相关的计算.了解完全平方公式和平方差格式的几何意义.掌握因式分解的方法,理解乘法公式在因式分解中的作用.了解代数和几何之间的转化关系,体会数与形之间的结合与变换规律. 理解同底数幂乘法、幂的乘方、积的乘方的概念,掌握三种幂的运算性质,能熟练地运用性质进行运算
掌握单项式与单项式相乘、单项式与多项式相乘、多项式与多项式相乘的法则,能正确、熟练地运用法则进行运算
理解同底数幂相除的概念,掌握同底数幂相除的法则,能熟练地进行同底数幂相除的运算
理解零次幂的底数不为零的意义
了解平方差公式的几何意义,掌握公式的结构特征,能正确运用公式进行运算
了解完全平方公式的几何意义,掌握公式的结构特征,能正确运用公式进行计算
课标要求 作业目标
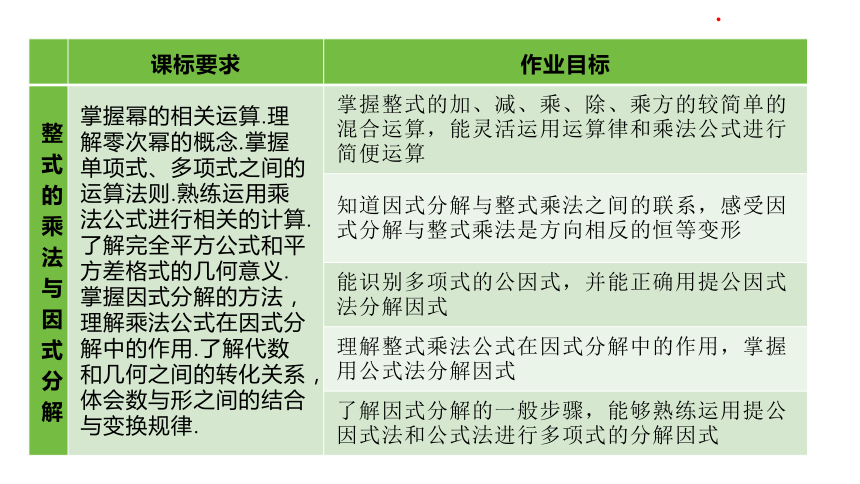
整式的乘法与因式分解 掌握幂的相关运算.理解零次幂的概念.掌握单项式、多项式之间的运算法则.熟练运用乘法公式进行相关的计算.了解完全平方公式和平方差格式的几何意义.掌握因式分解的方法,理解乘法公式在因式分解中的作用.了解代数和几何之间的转化关系,体会数与形之间的结合与变换规律. 掌握整式的加、减、乘、除、乘方的较简单的混合运算,能灵活运用运算律和乘法公式进行简便运算
知道因式分解与整式乘法之间的联系,感受因式分解与整式乘法是方向相反的恒等变形
能识别多项式的公因式,并能正确用提公因式法分解因式
理解整式乘法公式在因式分解中的作用,掌握用公式法分解因式
了解因式分解的一般步骤,能够熟练运用提公因式法和公式法进行多项式的分解因式
教材整合 核心归纳
02
第一单元 第2讲
1. (2024·深圳)下列运算正确的是( B )
A. (-m3)2=-m5 B. m2n·m=m3n
C. 3mn-m=3n D. (m-1)2=m2-1
2. (2024·河南)请写出2m的一个同类项: .
B
m(答案不唯一)
3. 因式分解:a2-7a= ;
x2+2x+1= ;
(a+1)2-4= .
a(a-7)
(x+1)2
(a+3)(a-1)
以题理知
4. 已知一串式子M:2a2b,-3ab2,a2bc,-2b+a2, x2y,
x3-2x-8,将其分别填在下面考点中对应的横线上.
判断下列代数式是否符合书
写要求:
①1 xy( × );
②ab÷c2( × ).
列代数式 关键是找出问题中的数量关系及公式,再列代数式
代数式求值 (1)直接代入法,如:已知
a=1,则a-1的值为 ;
(2)整体代入法,如:已知
a-b=2,则2a-2b的值为___
0
4
×
×
考点清单
考点 代数式及其求值
整式 式子串M中单项式有:
; x2y的系数为 ,次数为
式子串M中多项式有: ;
x3-2x-8是 次 项式,它的每一项分别是 ,二次项的系数为
同类
项 所含字母相同,且相同字母的指数也相同.式子串M中-a2b的同类项有
2a2b,-3ab2,a2bc,
x2y
3
-2b+a2,x3-2x-8
三
三
x3,-2x,-8
0
2a2b
思考:单独的
一个字母或一个
数是单项式吗?
如a,π,1等.
考点清单
考点 整式的相关概念
4. 已知一串式子M:2a2b,-3ab2,a2bc,-2b+a2, x2y,
x3-2x-8,将其分别填在下面考点中对应的横线上.
加减运算 如有括号就先去括号,然后再合并同类项
幂的运算
(m,n均为整数) 同底数幂的乘法:am·an= ;
同底数幂的除法:am÷an= ;
幂的乘方:(am)n= ;
积的乘方:(ab)n=
am+n
am-n
amn
anbn
考点清单
考点 ③ 整式的运算 【省卷T4,长沙T4,T18,T25】
整式乘除 单项式乘除:2a·a2b= ,
-3a3b÷ab= ;
多项式乘法:(a+b+c)m= ,
(m+n)(a+b)= ;
多项式除以单项式:(am-bm)÷m=
乘法公式 平方差公式:(a+b)(a-b)=
乘法公式 完全平方公式:(a±b)2=
2a3b
-3a2
ma+mb+mc
am+an+bm+bn
a-b
a2-b2
a2±2ab+b2
法则逆用:
(1)am+n=am·an;
(2)am-n=am÷an;
(3)amn=(am)n;
(4)anbn=(ab)n.
概念 把一个多项式化为几个整式的积的形式 提公因 式法 ma+mb=m(a+b), 如x2-23x= 因式分解要注意检查是否分解彻底,必须分解到每个因式不能再分解为止
公式法 平方差公式:a2-b2= ____________ 公式法 完全平方公式:
a2±2ab+b2= 十字相乘法 x2+(a+b)x+ab=(x+a)(x+b) x(x-23)
(a+b)(a-b)
考点清单
(a±b)2
考点 ④ 因式分解
重难精讲
变式探究
03
第一单元 第2讲
(2022·长沙)某校现需购买甲、乙两种读本共100本,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本.设购买
甲种读本x本,则购买乙种读本的费用为 元.
1. 某同学参加了 7.5 km 健康跑项目,他从起点开始以平均x km/min的速度跑了 10 min,此时他离健康跑终点的路程为 km.
8(100-x)
对点演练
(7.5-10x)
2. (2024·广州)若a2-2a-5=0,则2a2-4a+1= .
11
考点 代数式及其求值
(100-x)本
费用 = 单价×数量
8元/本
下列说法正确的是( B )
A. - 的次数是 2
B. - 的系数是-
C. x2+x-1的次数是3
D. x2与x属于同类项
3. (2022·永州)若单项式 3xmy 与 -2x6y 是同类项,
则 m= .
B
6
对点演练
考点 整式的相关概念
单项式的次数:所有字母的指数的和;
次数是 3
多项式的次数:多项式中次数最高项的次数;次数是 2
同类项:字母相同,并且相同字母的指数也相同.
一、幂的运算
(2024·湖南)下列计算正确的是( B )
A. 3a2-2a2=1 B. a3÷a2=a(a≠0)
C. a2·a3=a6 D. (2a)3=6a3
4. 计算(-a2)3÷(-a)2的结果是( D )
A. a3 B. -a2 C. a4 D. -a4
5. 若m,n满足3m-n-4=0,则8m÷2n= .
B
D
16
对点演练
考点 整式的相关概念
a2
a5
8a3
二、整式的混合运算
(6分)(2024·长沙)先化简,再求值:
2m-m(m-2)+(m+3)(m-3),其中m= .
【评分标准】
过程(2分)
结果(4分)
代入求值(6分)
解:原式=2m-m2+2m+m2-9
=4m-9.
当m= 时,原式=4× -9=10-9=1.
考点 整式的相关概念
6. 先化简,再求值:(2x+y)2-(2x+y)(2x-y)-2y(x+y),
其中x=( )2025,y=22024.
解:原式=4x2+4xy+y2-4x2+y2-2xy-2y2=2xy.
当x=( )2025,y=22024时,
原式=2×( )2025×22024=2× ×( )2024×22024=2× ×
( ×2)2024=2× ×12024=2× ×1=1.
解:原式=4x2+4xy+y2-4x2+y2-2xy-2y2=2xy.
当x=( )2025,y=22024 时,
原式=2×( )2025×22024=2× ×( )2024×22024
=2× ×( ×2)2024=2× ×12024=2× ×1=1.
对点演练
考点 整式的相关概念
三、乘法公式的灵活运用
已知(a-b)2=6,(a+b)2=4,则 a2+b2 的值为 .
【变式1】已知(x+y)2=25,(x-y)2=9,则 xy= .
【变式2】(2024·大庆)若a+ = ,则 a2+ 的值是 .
【变式3】★已知m2+n2+10=6m-2n,则m-n的值为 .
5
4
3
4
考点 整式的相关概念
(a+b)2+(a-b)2=2(a2+b2)
(x+y)2-(x-y)2=4xy
a2+b2 =
xy=
a2+=(a2+ )+2a·-2=(a- )2-2
a2+= (
m2-6m+9+n2+2n+1=0
(m-3)2+(n+1)2=0
m=3,
n=-1
m-n=4
完全平方公式的恒等变形:
a2+b2=(a+b)2-2ab=(a-b)2+2ab.
已知a+b(或a-b),ab,a2+b2中任意两个式子的值,均可通过公式变形求出另外一个式子的值.
考点 整式的相关概念
(2023·益阳)下列因式分解正确的是( A )
A. 2a2-4a+2=2(a-1)2
B. a2+ab+a=a(a+b)
C. 4a2-b2=(4a+b)(4a-b)
D. a3b-ab3=ab(a-b)2
A
考点 ④ 因式分解
a(a+b+1)
(2a+b)(2a-b)
ab(a2-b2)
=ab(a+b)(a-b)
7. 因式分解:
(1)2a2-2a= ;
(2)(2024·绥化)2mx2-8my2= .
8. (1)已知a+b=1,则a2-b2+2b+9的值为 ;
(2)(2024·广西)如果a+b=3,ab=1,那么a3b+2a2b2
+ab3的值为 .
2a(a-1)
2m(x+2y)(x-2y)
10
9
对点演练
考点 ④ 因式分解
8
字母“C”和“H”按照如下图所示的规律依次摆放,则第
个图形中字母“H”的个数是( B )
A. 2n B. 2n+2 C. 2n-2 D. 2n+1
B
考点 ⑤ 规律及代数推理【长沙T16】
4
H的个数:
对比①
对比②
4+2+2
④
4+2×3
4+2×2
4+2×(n-1)
n
2n+2
6
4+2
n
9. (2023·岳阳)观察下列式子:
12-1=1×0;22-2=2×1;32-3=3×2;42-4=4×3;52-
5=5×4;……
依此规律,则第n(n为正整数)个等式是 .
10. 若k为任意整数,则(2k+3)2-4k2的值总能( B )
A. 被2整除 B. 被3整除
C. 被5整除 D. 被7整除
n2-n=n(n- 1)
B
对点演练
考点 ⑤ 规律及代数推理【长沙T16】
12. 【课标素材题】(2024·雅安)如下图是1个纸杯和若干个
叠放在一起的纸杯的示意图,在探究纸杯叠放在一起后的总高
度H与杯子数量n的变化规律的活动中,我们可以获得以下数
据(字母):
±2
第12题图
①杯子底部到杯沿底边的高h;②杯口直径
D;③杯底直径d;④杯沿高a.请选用适当
的字母表示H= .
h+an
易错点·创新点
11. 已知y2-my+1是完全平方式,则m的值是 .
13. 观察下面的等式:32-12=8×1;52-32=8×2;72-52=
8×3;92-72=8×4;……
(1)写出192-172的结果;
解:(1)∵17=2×9-1,
∴192-172=8×9=72.
(2)按上面的规律归纳出一个一般的结论(用含n的等式表
示,n为正整数);
解:(2)由题意可得(2n+1)2-(2n-1)2=8n.
解:(1)∵17=2×9-1,
∴192-172=8×9=72.
解:(2)由题意可得(2n+1)2-(2n-1)2=8n.
易错点·创新点
(3)请运用有关知识,推理说明这个结论是正确的.
解:(3)∵(2n+1)2-(2n-1)2=[(2n+1)+(2n-
1)][(2n+1)-(2n-1)]=(2n+1+2n-1)(2n+1
-2n+1)=4n×2=8n,
∴(2n+1)2-(2n-1)2=8n正确.
解:(3)∵(2n+1)2-(2n-1)2
=[(2n+1)+(2n-1)][(2n+1)-(2n-1)]
=(2n+1+2n-1)(2n+1-2n+1)
=4n×2=8n,
∴(2n+1)2-(2n-1)2=8n正确.
易错点·创新点
课堂小结
代数式、整式
及因式分解
代数式及求值
整式的相关概念及运算
整式的加减
因式分解
单项式
多项式
整式
同类项
合并同类项
整式的乘除
第2讲 整式与因式分解
目录
CONTENTS
课标要求 作业目标
1
教材整合 核心归纳
2
重点精讲 变式探究
3
课标要求 作业目标
01
第一单元 第2讲
课标要求 作业目标
整式的加减 能分析具体问题中的简单数量关系,并用代数式表示,并会把具体数代入代数式求值.掌握单项式、多项式的相关概念,并能根据运算法则进行同类项的合并及相关的四则运算. 知道单项式的概念,会辨别单项式,能确定单项式的系数和次数
知道同类项的概念,能辨别几个单项式是否是同类项
掌握合并同类项的法则,会运用法则,并把单项式按某个字幕的升(降)幂排列
掌握去括号的规律,能运用规律进行整式的加减运算
掌握整式加减的运算法则,能运用法则进行整式的加减运算,并根据字母的值求整式的值
要求与目标
知道多项式和整式的概念,会辨别多项式和整式,能确定多项式的项数、次数和常数项
课标要求 作业目标
整式的乘法与因式分解 掌握幂的相关运算.理解零次幂的概念.掌握单项式、多项式之间的运算法则.熟练运用乘法公式进行相关的计算.了解完全平方公式和平方差格式的几何意义.掌握因式分解的方法,理解乘法公式在因式分解中的作用.了解代数和几何之间的转化关系,体会数与形之间的结合与变换规律. 理解同底数幂乘法、幂的乘方、积的乘方的概念,掌握三种幂的运算性质,能熟练地运用性质进行运算
掌握单项式与单项式相乘、单项式与多项式相乘、多项式与多项式相乘的法则,能正确、熟练地运用法则进行运算
理解同底数幂相除的概念,掌握同底数幂相除的法则,能熟练地进行同底数幂相除的运算
理解零次幂的底数不为零的意义
了解平方差公式的几何意义,掌握公式的结构特征,能正确运用公式进行运算
了解完全平方公式的几何意义,掌握公式的结构特征,能正确运用公式进行计算
课标要求 作业目标
整式的乘法与因式分解 掌握幂的相关运算.理解零次幂的概念.掌握单项式、多项式之间的运算法则.熟练运用乘法公式进行相关的计算.了解完全平方公式和平方差格式的几何意义.掌握因式分解的方法,理解乘法公式在因式分解中的作用.了解代数和几何之间的转化关系,体会数与形之间的结合与变换规律. 掌握整式的加、减、乘、除、乘方的较简单的混合运算,能灵活运用运算律和乘法公式进行简便运算
知道因式分解与整式乘法之间的联系,感受因式分解与整式乘法是方向相反的恒等变形
能识别多项式的公因式,并能正确用提公因式法分解因式
理解整式乘法公式在因式分解中的作用,掌握用公式法分解因式
了解因式分解的一般步骤,能够熟练运用提公因式法和公式法进行多项式的分解因式
教材整合 核心归纳
02
第一单元 第2讲
1. (2024·深圳)下列运算正确的是( B )
A. (-m3)2=-m5 B. m2n·m=m3n
C. 3mn-m=3n D. (m-1)2=m2-1
2. (2024·河南)请写出2m的一个同类项: .
B
m(答案不唯一)
3. 因式分解:a2-7a= ;
x2+2x+1= ;
(a+1)2-4= .
a(a-7)
(x+1)2
(a+3)(a-1)
以题理知
4. 已知一串式子M:2a2b,-3ab2,a2bc,-2b+a2, x2y,
x3-2x-8,将其分别填在下面考点中对应的横线上.
判断下列代数式是否符合书
写要求:
①1 xy( × );
②ab÷c2( × ).
列代数式 关键是找出问题中的数量关系及公式,再列代数式
代数式求值 (1)直接代入法,如:已知
a=1,则a-1的值为 ;
(2)整体代入法,如:已知
a-b=2,则2a-2b的值为___
0
4
×
×
考点清单
考点 代数式及其求值
整式 式子串M中单项式有:
; x2y的系数为 ,次数为
式子串M中多项式有: ;
x3-2x-8是 次 项式,它的每一项分别是 ,二次项的系数为
同类
项 所含字母相同,且相同字母的指数也相同.式子串M中-a2b的同类项有
2a2b,-3ab2,a2bc,
x2y
3
-2b+a2,x3-2x-8
三
三
x3,-2x,-8
0
2a2b
思考:单独的
一个字母或一个
数是单项式吗?
如a,π,1等.
考点清单
考点 整式的相关概念
4. 已知一串式子M:2a2b,-3ab2,a2bc,-2b+a2, x2y,
x3-2x-8,将其分别填在下面考点中对应的横线上.
加减运算 如有括号就先去括号,然后再合并同类项
幂的运算
(m,n均为整数) 同底数幂的乘法:am·an= ;
同底数幂的除法:am÷an= ;
幂的乘方:(am)n= ;
积的乘方:(ab)n=
am+n
am-n
amn
anbn
考点清单
考点 ③ 整式的运算 【省卷T4,长沙T4,T18,T25】
整式乘除 单项式乘除:2a·a2b= ,
-3a3b÷ab= ;
多项式乘法:(a+b+c)m= ,
(m+n)(a+b)= ;
多项式除以单项式:(am-bm)÷m=
乘法公式 平方差公式:(a+b)(a-b)=
乘法公式 完全平方公式:(a±b)2=
2a3b
-3a2
ma+mb+mc
am+an+bm+bn
a-b
a2-b2
a2±2ab+b2
法则逆用:
(1)am+n=am·an;
(2)am-n=am÷an;
(3)amn=(am)n;
(4)anbn=(ab)n.
概念 把一个多项式化为几个整式的积的形式 提公因 式法 ma+mb=m(a+b), 如x2-23x= 因式分解要注意检查是否分解彻底,必须分解到每个因式不能再分解为止
公式法 平方差公式:a2-b2= ____________ 公式法 完全平方公式:
a2±2ab+b2= 十字相乘法 x2+(a+b)x+ab=(x+a)(x+b) x(x-23)
(a+b)(a-b)
考点清单
(a±b)2
考点 ④ 因式分解
重难精讲
变式探究
03
第一单元 第2讲
(2022·长沙)某校现需购买甲、乙两种读本共100本,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本.设购买
甲种读本x本,则购买乙种读本的费用为 元.
1. 某同学参加了 7.5 km 健康跑项目,他从起点开始以平均x km/min的速度跑了 10 min,此时他离健康跑终点的路程为 km.
8(100-x)
对点演练
(7.5-10x)
2. (2024·广州)若a2-2a-5=0,则2a2-4a+1= .
11
考点 代数式及其求值
(100-x)本
费用 = 单价×数量
8元/本
下列说法正确的是( B )
A. - 的次数是 2
B. - 的系数是-
C. x2+x-1的次数是3
D. x2与x属于同类项
3. (2022·永州)若单项式 3xmy 与 -2x6y 是同类项,
则 m= .
B
6
对点演练
考点 整式的相关概念
单项式的次数:所有字母的指数的和;
次数是 3
多项式的次数:多项式中次数最高项的次数;次数是 2
同类项:字母相同,并且相同字母的指数也相同.
一、幂的运算
(2024·湖南)下列计算正确的是( B )
A. 3a2-2a2=1 B. a3÷a2=a(a≠0)
C. a2·a3=a6 D. (2a)3=6a3
4. 计算(-a2)3÷(-a)2的结果是( D )
A. a3 B. -a2 C. a4 D. -a4
5. 若m,n满足3m-n-4=0,则8m÷2n= .
B
D
16
对点演练
考点 整式的相关概念
a2
a5
8a3
二、整式的混合运算
(6分)(2024·长沙)先化简,再求值:
2m-m(m-2)+(m+3)(m-3),其中m= .
【评分标准】
过程(2分)
结果(4分)
代入求值(6分)
解:原式=2m-m2+2m+m2-9
=4m-9.
当m= 时,原式=4× -9=10-9=1.
考点 整式的相关概念
6. 先化简,再求值:(2x+y)2-(2x+y)(2x-y)-2y(x+y),
其中x=( )2025,y=22024.
解:原式=4x2+4xy+y2-4x2+y2-2xy-2y2=2xy.
当x=( )2025,y=22024时,
原式=2×( )2025×22024=2× ×( )2024×22024=2× ×
( ×2)2024=2× ×12024=2× ×1=1.
解:原式=4x2+4xy+y2-4x2+y2-2xy-2y2=2xy.
当x=( )2025,y=22024 时,
原式=2×( )2025×22024=2× ×( )2024×22024
=2× ×( ×2)2024=2× ×12024=2× ×1=1.
对点演练
考点 整式的相关概念
三、乘法公式的灵活运用
已知(a-b)2=6,(a+b)2=4,则 a2+b2 的值为 .
【变式1】已知(x+y)2=25,(x-y)2=9,则 xy= .
【变式2】(2024·大庆)若a+ = ,则 a2+ 的值是 .
【变式3】★已知m2+n2+10=6m-2n,则m-n的值为 .
5
4
3
4
考点 整式的相关概念
(a+b)2+(a-b)2=2(a2+b2)
(x+y)2-(x-y)2=4xy
a2+b2 =
xy=
a2+=(a2+ )+2a·-2=(a- )2-2
a2+= (
m2-6m+9+n2+2n+1=0
(m-3)2+(n+1)2=0
m=3,
n=-1
m-n=4
完全平方公式的恒等变形:
a2+b2=(a+b)2-2ab=(a-b)2+2ab.
已知a+b(或a-b),ab,a2+b2中任意两个式子的值,均可通过公式变形求出另外一个式子的值.
考点 整式的相关概念
(2023·益阳)下列因式分解正确的是( A )
A. 2a2-4a+2=2(a-1)2
B. a2+ab+a=a(a+b)
C. 4a2-b2=(4a+b)(4a-b)
D. a3b-ab3=ab(a-b)2
A
考点 ④ 因式分解
a(a+b+1)
(2a+b)(2a-b)
ab(a2-b2)
=ab(a+b)(a-b)
7. 因式分解:
(1)2a2-2a= ;
(2)(2024·绥化)2mx2-8my2= .
8. (1)已知a+b=1,则a2-b2+2b+9的值为 ;
(2)(2024·广西)如果a+b=3,ab=1,那么a3b+2a2b2
+ab3的值为 .
2a(a-1)
2m(x+2y)(x-2y)
10
9
对点演练
考点 ④ 因式分解
8
字母“C”和“H”按照如下图所示的规律依次摆放,则第
个图形中字母“H”的个数是( B )
A. 2n B. 2n+2 C. 2n-2 D. 2n+1
B
考点 ⑤ 规律及代数推理【长沙T16】
4
H的个数:
对比①
对比②
4+2+2
④
4+2×3
4+2×2
4+2×(n-1)
n
2n+2
6
4+2
n
9. (2023·岳阳)观察下列式子:
12-1=1×0;22-2=2×1;32-3=3×2;42-4=4×3;52-
5=5×4;……
依此规律,则第n(n为正整数)个等式是 .
10. 若k为任意整数,则(2k+3)2-4k2的值总能( B )
A. 被2整除 B. 被3整除
C. 被5整除 D. 被7整除
n2-n=n(n- 1)
B
对点演练
考点 ⑤ 规律及代数推理【长沙T16】
12. 【课标素材题】(2024·雅安)如下图是1个纸杯和若干个
叠放在一起的纸杯的示意图,在探究纸杯叠放在一起后的总高
度H与杯子数量n的变化规律的活动中,我们可以获得以下数
据(字母):
±2
第12题图
①杯子底部到杯沿底边的高h;②杯口直径
D;③杯底直径d;④杯沿高a.请选用适当
的字母表示H= .
h+an
易错点·创新点
11. 已知y2-my+1是完全平方式,则m的值是 .
13. 观察下面的等式:32-12=8×1;52-32=8×2;72-52=
8×3;92-72=8×4;……
(1)写出192-172的结果;
解:(1)∵17=2×9-1,
∴192-172=8×9=72.
(2)按上面的规律归纳出一个一般的结论(用含n的等式表
示,n为正整数);
解:(2)由题意可得(2n+1)2-(2n-1)2=8n.
解:(1)∵17=2×9-1,
∴192-172=8×9=72.
解:(2)由题意可得(2n+1)2-(2n-1)2=8n.
易错点·创新点
(3)请运用有关知识,推理说明这个结论是正确的.
解:(3)∵(2n+1)2-(2n-1)2=[(2n+1)+(2n-
1)][(2n+1)-(2n-1)]=(2n+1+2n-1)(2n+1
-2n+1)=4n×2=8n,
∴(2n+1)2-(2n-1)2=8n正确.
解:(3)∵(2n+1)2-(2n-1)2
=[(2n+1)+(2n-1)][(2n+1)-(2n-1)]
=(2n+1+2n-1)(2n+1-2n+1)
=4n×2=8n,
∴(2n+1)2-(2n-1)2=8n正确.
易错点·创新点
课堂小结
代数式、整式
及因式分解
代数式及求值
整式的相关概念及运算
整式的加减
因式分解
单项式
多项式
整式
同类项
合并同类项
整式的乘除
同课章节目录
