第5讲 一次方程(组) 2025年中考数学专题复习课件(共25张PPT)(湖南)
文档属性
| 名称 | 第5讲 一次方程(组) 2025年中考数学专题复习课件(共25张PPT)(湖南) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 21:27:31 | ||
图片预览








文档简介
(共25张PPT)
第5讲 一次方程(组)
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第二单元 第5讲
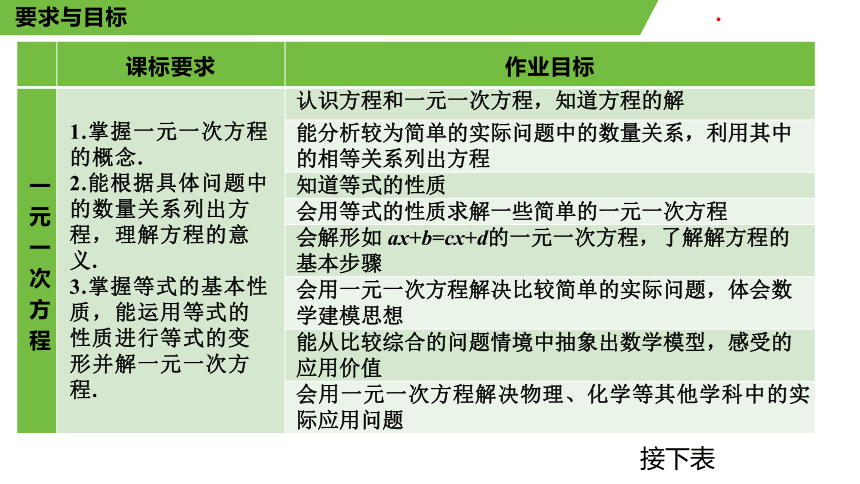
课标要求 作业目标
一元一次方程 1.掌握一元一次方程的概念. 2.能根据具体问题中的数量关系列出方程,理解方程的意义. 3.掌握等式的基本性质,能运用等式的性质进行等式的变形并解一元一次方程. 认识方程和一元一次方程,知道方程的解
能分析较为简单的实际问题中的数量关系,利用其中的相等关系列出方程
知道等式的性质
会用等式的性质求解一些简单的一元一次方程
会解形如 ax+b=cx+d的一元一次方程,了解解方程的基本步骤
会用一元一次方程解决比较简单的实际问题,体会数学建模思想
能从比较综合的问题情境中抽象出数学模型,感受的应用价值
会用一元一次方程解决物理、化学等其他学科中的实际应用问题
要求与目标
接下表
课标要求 作业目标
二元一次方程组 1.根据具体问题中的数量关系列出方程,理解方程的意义. 2.掌握等式的基本性质,能运用等式的性质进行等式的变形,能根据的性质解一元一次方程. 3.能根据二元一次方程组的特征,选择代入消元法或加减消元法解二元一次方程组. 辨别二元一次方程组,辨别二元一次方程(组)的解
能根据所给的二元一次方程,将一个未知数用含另一个未知数的式子表示
会用代入法、加减法解二元一次方程组,体会“消元”思想
能根据一次方程组的具体形式选择适当的解法并对一次方程组有灵活变形的能力
会用一次方程组解决比较简单的实际问题,体会数学建模的思想
能从比较综合的问题情境中抽象出数学模型,体会数学应用的价值
判别三元一次方程组(*),能解简单的三元一次方程组(*)
要求与目标
教材整合 核心归纳
02
第二单元 第5讲
(2)设鸡有x只,兔有y只,根据鸡、兔共200只可得方程为
②,根据鸡、兔足数共560只,可得方程为
③,联立②③所得方程组的解为 .
(1) 设鸡有x只,则可列方程为 ①,
方程①的解为 ;
2x+4(200-x)=560
x=120
x+y=200
2x+4y=560
张奶奶养鸡、兔共 200 只,鸡、兔足数共 560 只,求鸡、兔各有多少只.
兔有(200-x)只
等式的基 本性质 性质1:若a=b,则a±c=
性质2:若a=b,则ac= ,
若a=b(c≠0),则 =
性质3:若a=b,则b=a(对称性)
性质4:若a=b,b=c,则a=c(传递性)
b±c
bc
考点 等式的性质
考点清单
考点 解一次方程(组)
方程的基 本概念 一元一次
方程 只含有一个未知数,并且未知数的次数是1的整式方程.如【以题理知】中方程 (填序号)
二元一次
方程 含有两个未知数,并且含未知数的项次数都是1的整式方程.如【以题理知】中的方程 (填序号)
二元一次
方程组 含有两个未知数,并且所含未知数的项的次数是1的两个方程构成的方程组
方程(组)
的解 使方程(组)两边相等的未知数的值.如:写出方程②的一组整数解为
①
②③
(答案不唯一)
考点清单
解一次方程(组) 解一元一次方程的步骤 ①去分母(不要漏乘不含分母的项);
②去括号(若括号前为负号,去括号后注意变号);③移项(要变号);④合并同类项;⑤系数化为1
解方程组的方法 (1)代入消元法、加减消元法、图象法;
(2)技法:已知方程组求代数式的值时,注意观察方程系数特点,有时可利用整体思想不解方程求值.如:已知
则x-y= ,x+y=
考点 解一次方程(组)
1
3
思考:每一步的依据是什么
考点清单
常考类型 等量关系 一般步骤
销售
问题 售价=标价× (如打8折即标价×0.8); 销售额=售价×销量;利润=售价-进价(成本); 利润率=利润÷进价×100% 审题;
设未知数;
列方程(组);
解方程(组);
检验;
作答
购买问题 总价=单价×数量;甲的数量+乙的数量=总数量 工程问题 工作量=工作效率×工作时间 行程
问题 路程=速度×时间; 相遇问题:全程=甲走的路程+乙走的路程; 追及问题:①同地不同时出发:前者走的路程=追者走的路程; ②同时不同地出发:前者走的路程+两人出发点的间距=追者走的路程 考点 一次方程(组)的应用【省卷T23,长沙T22】
考点清单
重难精讲
变式探究
03
第二单元 第5讲
例1根据等式的性质,下列各式变形正确的是( A )
A. 若 = ,则a=b
B. 若ac=bc,则a=b
C. 若a2=b2,则a=b
D. 若- x=6,则x=-2
A
等式两边都乘c,结果仍相等
c可能为0
a,b可能互为相反数
x=-18
例2(6分)解方程: - =1.
【一般步骤】
去分母
去括号(2分)
移项、合并同类项
系数化为1(6分)
解:去分母,得3(x+2)-2(2x-1)=12.
去括号,得3x+6-4x+2=12.
移项、合并同类项,得-x=4.
系数化为1,得x=-4.
×12
×12
×12
例3 (6分)用指定方法解方程组:
(1)代入消元法:
代入②式得x-2(3x+4)=-3,
解得x=-1.
【评分标准】
求解x和y(5分)
写解(6分)
解:由①式得y=3x+4③,
代入②式得x-2(3x+4)=-3,
解得x=-1.
将x=-1代入③式得y=1.
∴方程组的解为
∴方程组的解为
(2)加减消元法:
解:①×2-②得5x=-5,解得x=-1.
把x=-1代入①式得3×(-1)-y=-4,解得y=1.
∴方程组的解为
解:①×2-②得5x=-5,解得x=-1.
把x=-1代入①式得3×(-1)-y=-4,解得y=1.
∴方程组的解为
例3 (6分)用指定方法解方程组:
(1)求得解后,将解代回原方程(组)进行验算;
(2)去分母时,方程两边每一项都要乘分母的最小公倍数,注意
不要漏乘不含分母的项;
(3)去分母时,分子若是两项或两项以上,应该看作一个整体,
去分母时应加上括号.
1. (2023·永州)关于 x 的一元一次方程 2x+m=5 的解为 x=1,
则m的值为( A )
A. 3 B. -3 C. 7 D. -7
A
2. 解方程组:
解:①×2得4x+6y=26③,
②×3得9x-6y=0④,
③+④得13x=26,解得x=2.
把x=2代入①得4+3y=13,解得y=3.
故原方程组的解是
解:①×2得4x+6y=26③,
②×3得9x-6y=0④,
③+④得13x=26,解得x=2.
把x=2代入①得4+3y=13,解得y=3.
故原方程组的解是
代入
2+m=5
m=3
例4 (6分) (2024·安徽) 乡村振兴战略实施以来,很多外出人员返乡创业.某村有部分返乡青年承包了一些田地,采用新技术种植A,B两种农作物.种植这两种农作物每公顷所需人数和投入资金如下表:
农作物品种 每公顷所需人数 每公顷所需投
入资金(万元)
A 4 8
B 3 9
已知农作物种植人员共24位,且每人只参与一种农作物种植,投入资金共60万元,问A,B这两种农作物的种植面积各多少公顷?
设A种农作物的种植面积是x公顷,B种农作物的种植面积是y公顷.
A种总人数+B种总人数=24
A种总资金+B种总资金=60
4x
3y
8x
9y
农作物种植人员共24位,投入资金共60万元
解得
【评分标准】
设(1分)
列(3分)
解(5分)
答(6分)
解:设A种农作物的种植面积是x公顷,
B种农作物的种植面积是y公顷.
根据题意得
解得
答:A种农作物的种植面积是3公顷,
B种农作物的种植面积是4公顷.
农作物品种 每公顷所需人数 每公顷所需投入资金(万元)
A 4 8
B 3 9
3. 某商品的进价为每件10元,若按标价打八折售出后,每件可
获利2元,则该商品的标价为每件 元.
15
4. (2024·扬州)《九章算术》是中国古代的数学专著,是《算经
十书》中最重要的一部,书中第八章内容“方程”里记载了一
个有趣的追及问题,可理解为:速度快的人每分钟走100米,
速度慢的人每分钟走60米,现在速度慢的人先走100米,速度
快的人去追他.则速度快的人追上他需要 分钟.
2.5
5. 【整体思想】已知关于x,y的二元一次方程组 的解满足x-y=4,则m的值为( B )
A. 0 B. 1 C. 2 D. 3
B
,
2x-2y=2m+6
代入
x-y=m+3
m+3=4
m=1
6. 新角度几何新定义如果一个矩形内部能用一些正方形铺满,
既不重叠,又无缝隙,就称它为“优美矩形”.如右图所示,
“优美矩形”ABCD的周长为26,则正方形b的边长为 .
第6题图
【辅助设问】设正方形b的边长为x,用含x的式子分别表示出
a,c,d的边长,然后可得到关于x的方程: .
1
2(8x+5x)= 26
7. 【整体思想】(2024·长沙节选)已知两个不同的点A(x1,
y1),B(x2,y2)都在关于x的函数y=ax2+bx+c(a,b,c是常
数,a≠0)的图象上.当A,B两点的坐标分别为(-1,-4),
(3,4)时,求代数式2024a+1012b+ 的值.
解:将点A(-1,-4),B(3,4)代入y=ax2+bx+c得
②-①得8a+4b=8,即2a+b=2.
∴2024a+1012b+ =1012(2a+b)+ =2024 .
解:将点A(-1,-4),B(3,4)代入y=ax2+bx+c得
②-①得8a+4b=8,即2a+b=2.
∴2024a+1012b+ =1012(2a+b)+ =2024 .
课堂小结
一次方程(组)
等式的性质
一元一次方程的定义
一元一次方程
二元一次方程(组)
一次方程(组)的应用
解一元一次方程的一般步骤和注意事项
二元一次方程(组)的相关概念
解二元一次方程组的基本思想
二(三)元一次方程组的解法
第5讲 一次方程(组)
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第二单元 第5讲
课标要求 作业目标
一元一次方程 1.掌握一元一次方程的概念. 2.能根据具体问题中的数量关系列出方程,理解方程的意义. 3.掌握等式的基本性质,能运用等式的性质进行等式的变形并解一元一次方程. 认识方程和一元一次方程,知道方程的解
能分析较为简单的实际问题中的数量关系,利用其中的相等关系列出方程
知道等式的性质
会用等式的性质求解一些简单的一元一次方程
会解形如 ax+b=cx+d的一元一次方程,了解解方程的基本步骤
会用一元一次方程解决比较简单的实际问题,体会数学建模思想
能从比较综合的问题情境中抽象出数学模型,感受的应用价值
会用一元一次方程解决物理、化学等其他学科中的实际应用问题
要求与目标
接下表
课标要求 作业目标
二元一次方程组 1.根据具体问题中的数量关系列出方程,理解方程的意义. 2.掌握等式的基本性质,能运用等式的性质进行等式的变形,能根据的性质解一元一次方程. 3.能根据二元一次方程组的特征,选择代入消元法或加减消元法解二元一次方程组. 辨别二元一次方程组,辨别二元一次方程(组)的解
能根据所给的二元一次方程,将一个未知数用含另一个未知数的式子表示
会用代入法、加减法解二元一次方程组,体会“消元”思想
能根据一次方程组的具体形式选择适当的解法并对一次方程组有灵活变形的能力
会用一次方程组解决比较简单的实际问题,体会数学建模的思想
能从比较综合的问题情境中抽象出数学模型,体会数学应用的价值
判别三元一次方程组(*),能解简单的三元一次方程组(*)
要求与目标
教材整合 核心归纳
02
第二单元 第5讲
(2)设鸡有x只,兔有y只,根据鸡、兔共200只可得方程为
②,根据鸡、兔足数共560只,可得方程为
③,联立②③所得方程组的解为 .
(1) 设鸡有x只,则可列方程为 ①,
方程①的解为 ;
2x+4(200-x)=560
x=120
x+y=200
2x+4y=560
张奶奶养鸡、兔共 200 只,鸡、兔足数共 560 只,求鸡、兔各有多少只.
兔有(200-x)只
等式的基 本性质 性质1:若a=b,则a±c=
性质2:若a=b,则ac= ,
若a=b(c≠0),则 =
性质3:若a=b,则b=a(对称性)
性质4:若a=b,b=c,则a=c(传递性)
b±c
bc
考点 等式的性质
考点清单
考点 解一次方程(组)
方程的基 本概念 一元一次
方程 只含有一个未知数,并且未知数的次数是1的整式方程.如【以题理知】中方程 (填序号)
二元一次
方程 含有两个未知数,并且含未知数的项次数都是1的整式方程.如【以题理知】中的方程 (填序号)
二元一次
方程组 含有两个未知数,并且所含未知数的项的次数是1的两个方程构成的方程组
方程(组)
的解 使方程(组)两边相等的未知数的值.如:写出方程②的一组整数解为
①
②③
(答案不唯一)
考点清单
解一次方程(组) 解一元一次方程的步骤 ①去分母(不要漏乘不含分母的项);
②去括号(若括号前为负号,去括号后注意变号);③移项(要变号);④合并同类项;⑤系数化为1
解方程组的方法 (1)代入消元法、加减消元法、图象法;
(2)技法:已知方程组求代数式的值时,注意观察方程系数特点,有时可利用整体思想不解方程求值.如:已知
则x-y= ,x+y=
考点 解一次方程(组)
1
3
思考:每一步的依据是什么
考点清单
常考类型 等量关系 一般步骤
销售
问题 售价=标价× (如打8折即标价×0.8); 销售额=售价×销量;利润=售价-进价(成本); 利润率=利润÷进价×100% 审题;
设未知数;
列方程(组);
解方程(组);
检验;
作答
购买问题 总价=单价×数量;甲的数量+乙的数量=总数量 工程问题 工作量=工作效率×工作时间 行程
问题 路程=速度×时间; 相遇问题:全程=甲走的路程+乙走的路程; 追及问题:①同地不同时出发:前者走的路程=追者走的路程; ②同时不同地出发:前者走的路程+两人出发点的间距=追者走的路程 考点 一次方程(组)的应用【省卷T23,长沙T22】
考点清单
重难精讲
变式探究
03
第二单元 第5讲
例1根据等式的性质,下列各式变形正确的是( A )
A. 若 = ,则a=b
B. 若ac=bc,则a=b
C. 若a2=b2,则a=b
D. 若- x=6,则x=-2
A
等式两边都乘c,结果仍相等
c可能为0
a,b可能互为相反数
x=-18
例2(6分)解方程: - =1.
【一般步骤】
去分母
去括号(2分)
移项、合并同类项
系数化为1(6分)
解:去分母,得3(x+2)-2(2x-1)=12.
去括号,得3x+6-4x+2=12.
移项、合并同类项,得-x=4.
系数化为1,得x=-4.
×12
×12
×12
例3 (6分)用指定方法解方程组:
(1)代入消元法:
代入②式得x-2(3x+4)=-3,
解得x=-1.
【评分标准】
求解x和y(5分)
写解(6分)
解:由①式得y=3x+4③,
代入②式得x-2(3x+4)=-3,
解得x=-1.
将x=-1代入③式得y=1.
∴方程组的解为
∴方程组的解为
(2)加减消元法:
解:①×2-②得5x=-5,解得x=-1.
把x=-1代入①式得3×(-1)-y=-4,解得y=1.
∴方程组的解为
解:①×2-②得5x=-5,解得x=-1.
把x=-1代入①式得3×(-1)-y=-4,解得y=1.
∴方程组的解为
例3 (6分)用指定方法解方程组:
(1)求得解后,将解代回原方程(组)进行验算;
(2)去分母时,方程两边每一项都要乘分母的最小公倍数,注意
不要漏乘不含分母的项;
(3)去分母时,分子若是两项或两项以上,应该看作一个整体,
去分母时应加上括号.
1. (2023·永州)关于 x 的一元一次方程 2x+m=5 的解为 x=1,
则m的值为( A )
A. 3 B. -3 C. 7 D. -7
A
2. 解方程组:
解:①×2得4x+6y=26③,
②×3得9x-6y=0④,
③+④得13x=26,解得x=2.
把x=2代入①得4+3y=13,解得y=3.
故原方程组的解是
解:①×2得4x+6y=26③,
②×3得9x-6y=0④,
③+④得13x=26,解得x=2.
把x=2代入①得4+3y=13,解得y=3.
故原方程组的解是
代入
2+m=5
m=3
例4 (6分) (2024·安徽) 乡村振兴战略实施以来,很多外出人员返乡创业.某村有部分返乡青年承包了一些田地,采用新技术种植A,B两种农作物.种植这两种农作物每公顷所需人数和投入资金如下表:
农作物品种 每公顷所需人数 每公顷所需投
入资金(万元)
A 4 8
B 3 9
已知农作物种植人员共24位,且每人只参与一种农作物种植,投入资金共60万元,问A,B这两种农作物的种植面积各多少公顷?
设A种农作物的种植面积是x公顷,B种农作物的种植面积是y公顷.
A种总人数+B种总人数=24
A种总资金+B种总资金=60
4x
3y
8x
9y
农作物种植人员共24位,投入资金共60万元
解得
【评分标准】
设(1分)
列(3分)
解(5分)
答(6分)
解:设A种农作物的种植面积是x公顷,
B种农作物的种植面积是y公顷.
根据题意得
解得
答:A种农作物的种植面积是3公顷,
B种农作物的种植面积是4公顷.
农作物品种 每公顷所需人数 每公顷所需投入资金(万元)
A 4 8
B 3 9
3. 某商品的进价为每件10元,若按标价打八折售出后,每件可
获利2元,则该商品的标价为每件 元.
15
4. (2024·扬州)《九章算术》是中国古代的数学专著,是《算经
十书》中最重要的一部,书中第八章内容“方程”里记载了一
个有趣的追及问题,可理解为:速度快的人每分钟走100米,
速度慢的人每分钟走60米,现在速度慢的人先走100米,速度
快的人去追他.则速度快的人追上他需要 分钟.
2.5
5. 【整体思想】已知关于x,y的二元一次方程组 的解满足x-y=4,则m的值为( B )
A. 0 B. 1 C. 2 D. 3
B
,
2x-2y=2m+6
代入
x-y=m+3
m+3=4
m=1
6. 新角度几何新定义如果一个矩形内部能用一些正方形铺满,
既不重叠,又无缝隙,就称它为“优美矩形”.如右图所示,
“优美矩形”ABCD的周长为26,则正方形b的边长为 .
第6题图
【辅助设问】设正方形b的边长为x,用含x的式子分别表示出
a,c,d的边长,然后可得到关于x的方程: .
1
2(8x+5x)= 26
7. 【整体思想】(2024·长沙节选)已知两个不同的点A(x1,
y1),B(x2,y2)都在关于x的函数y=ax2+bx+c(a,b,c是常
数,a≠0)的图象上.当A,B两点的坐标分别为(-1,-4),
(3,4)时,求代数式2024a+1012b+ 的值.
解:将点A(-1,-4),B(3,4)代入y=ax2+bx+c得
②-①得8a+4b=8,即2a+b=2.
∴2024a+1012b+ =1012(2a+b)+ =2024 .
解:将点A(-1,-4),B(3,4)代入y=ax2+bx+c得
②-①得8a+4b=8,即2a+b=2.
∴2024a+1012b+ =1012(2a+b)+ =2024 .
课堂小结
一次方程(组)
等式的性质
一元一次方程的定义
一元一次方程
二元一次方程(组)
一次方程(组)的应用
解一元一次方程的一般步骤和注意事项
二元一次方程(组)的相关概念
解二元一次方程组的基本思想
二(三)元一次方程组的解法
同课章节目录
