第8讲 一元一次不等式(组) 2025年中考一轮数学专题复习课件(共24张PPT)(湖南)
文档属性
| 名称 | 第8讲 一元一次不等式(组) 2025年中考一轮数学专题复习课件(共24张PPT)(湖南) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
第8讲 一元一次不等式(组)
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第二单元 第8讲
课标要求 作业目标
一元一次不等式 (组) 1.了解不等式的意义,探索不等式的基本性质. 2.能解数字系数的一元一次不等式,能根据具体问题中的数量关系,列出一元一次不等式,解决简单的问题. 能够说明一元一次不等式及其相关概念
识记解一元一次不等式的一般步骤,掌握一元一次不等式的解法
能够在数轴上表示出一元一次不等式的解集
了解不等式组及相关概念
会解由两个一元一次不等式组成的不等式组,并会用数轴确定解集
能根据实际问题中的数量关系,列出一元一次不等式(组),解决实际问题
根据方程和不等式的关系,整理归纳并解决综合问题
要求与目标
教材整合 核心归纳
02
第二单元 第8讲
不等式
的基本
性质 性质1:若a>b,则a±c b±c
性质2:若a>b,c>0,则ac bc,
性质3:若a>b,c<0,则ac bc,
>
>
>
<
<
考点 不等式的基本性质
考点清单
一元
一次 不等
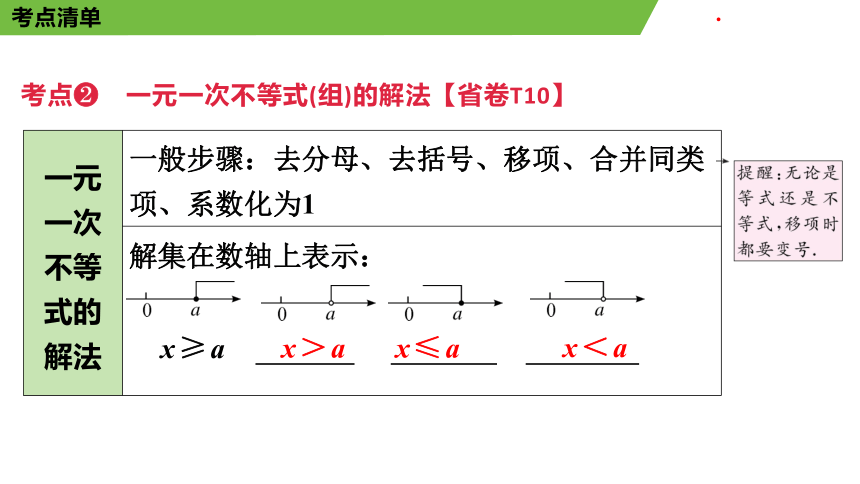
式的 解法 一般步骤:去分母、去括号、移项、合并同类项、系数化为1
解集在数轴上表示:
x≥a
x>a
x≤a
x<a
考点 一元一次不等式(组)的解法【省卷T10】
考点清单
一元一次 不等式组 的解法 一般步骤:先分别解出每个一元一次不等式的解集,再求出它们解集的公共部分 解 集 在 数 轴 上 表 示 类型(a>b) 口诀 图示 解集
同大取大
x>a
同小取小
_________
小大大小取中间 __________
大大小小取不了 无解
考点 一元一次不等式(组)的解法【省卷T10】
x<b
b<x<a
考点清单
一般
步骤 审题、设未知数、找不等关系、列不等式、解不等式、检验是否符合实际、作答
关
键
词 实际问题中,出现至少、不低于、不小于(≥);最多、不高于、不大于(≤);大于、多于、超过、高于(>);少于、小于、不足、低于(<)等,一般利用不等式解题
考点 一元一次不等式的实际应用 省卷T23,长沙T22】
考点清单
重难精讲
变式探究
03
第二单元 第8讲
例1 解不等式组请结合题意解答本题
(每空只需填出最后结果).
解:解不等式①,得 ;解不等式②,得 .
把不等式①和②的解集在下面的数轴上表示出来:
所以原不等式组的解集为 .
x>-2
x≤3
-2<x≤3
例2 改编问题链 已知关于x的不等式组
(1)若该不等式组的解集为-1<x≤3,则a的值为 ;
(2)若该不等式组无解,则a的取值范围为 ;
-3
a≥1
(3)若该不等式组的整数解有3个,则a的取值范围为 .
-2≤a<-1
x>a+2
x≤3
a+2=-1
a=-3
大大小小取不了
a+2≥3
a≥1
3,2,1
0≤a+2<1
-2≤a<-1
易错1:在数轴上表示不等式(组)的解集时,“<”“>”的边
界点用空心点,“≤”“≥”的边界点用实心点.
易错2:含参问题中,求参数的取值范围时,要注意边界点是
否取等号.
1. (2024·上海)如果x>y,那么下列正确的是( C )
A. x+5≤y+5 B. x-5<y-5
C. 5x>5y D.-5x>-5y
2. 如下图,数轴上的两点A,B对应的实数分别是a,b,则
下列式子中成立的是( A )
A. 1-2a>1-2b B. -a<-b
C. a+b<0 D. |a|-|b|>0
第2题图
C
A
3. (2024·湖北)不等式 x+1≥2 的解集在数轴上表示正确的是
( A )
4. (2024·南充)若关于x的不等式组的解集为x<3,
则m的取值范围是( B )
A. m>0 B. m≥2
C. m<2 D. m≤2
A
B
x<3
同小取小
m+1≥3
m≥2
5. (2024·扬州)解不等式组并求出它的所有整数
解的和.
解:解不等式2x-6≤0,得x≤3.
解不等式x< ,得x> .
所以不等式组的解集为 <x≤3.
所以整数解为1,2,3,整数解的和为6.
解:解不等式2x-6≤0,得x≤3.
解不等式x< ,得x> .
所以不等式组的解集为 <x≤3.
所以整数解为1,2,3,整数解的和为6.
6. 某品牌护眼灯的进价为240元,商店以320元的价格出售.“五一”假日期间,商店为让利于顾客,计划以利润率不低于20%的价格降价出售,则该护眼灯最多可降价 元.
32
不等关系
利润率=利润÷进价×100%
设可降价 a 元
×100%≥20%
a ≤32
(1)求A种湘绣作品和B种湘绣作品的单价分别为多少元;
解:(1)设A种湘绣作品的单价为x元,
B种湘绣作品的单价为y元.
根据题意得解得
答:A种湘绣作品的单价为300元,
B种湘绣作品的单价为200元.
7. (2024·长沙)刺绣是我国民间传统手工艺,湘绣作为中国四大
刺绣之一,闻名中外.在巴黎奥运会倒计时50天之际,某国际
旅游公司计划购买A,B两种奥运主题的湘绣作品作为纪念品.
已知购买1件A种湘绣作品与2件B种湘绣作品共需要700元,
购买2件A种湘绣作品与3件B种湘绣作品共需要1200元.
(2)该国际旅游公司计划购买A种湘绣作品和B种湘绣作品共200件,总费用不超过50000元,那么最多能购买A种湘绣作品多少件?
解:(2)设购买A种湘绣作品m件,则购买B种湘绣作品(200-m)件.
根据题意得300m+200(200-m)≤50000,
解得m≤100.
∴m的最大值为100.
答:最多能购买A种湘绣作品100件.
7. (2024·长沙)刺绣是我国民间传统手工艺,湘绣作为中国四大刺绣之一,闻名中外.在巴黎奥运会倒计时50天之际,某国际旅游公司计划购买A,B两种奥运主题的湘绣作品作为纪念品.已知购买1件A种湘绣作品与2件B种湘绣作品共需要700元,购买2件A种湘绣作品与3件B种湘绣作品共需要1200元.
8. 关于x,y的方程组的解中x与y的和不
小于5,则k的取值范围为( A )
A. k≥8 B. k>8 C. k≤8 D. k<8
A
9. (2024·湖南)在平面直角坐标系xOy中,对于点P(x,y),若
x,y均为整数,则称点P为“整点”.特别地,当 (其中
xy≠0)的值为整数时,称“整点”P为“超整点”.已知点
P(2a-4,a+3)在第二象限,下列说法正确的是( C )
A. a<-3
B. 若点P为“整点”,则点P的个数为3个
C. 若点P为“超整点”,则点P的个数为1个
D. 若点P为“超整点”,则点P到两坐标轴的距离之和大于10
C
10. (2023·长沙)为提升学生身体素质,落实教育部门“在校学
生每天锻炼时间不少于1小时”的文件精神.某校利用课后服务
时间,在八年级开展“体育赋能,助力成长”班级篮球赛,共
16个班级参加.
(1)比赛积分规定:每场比赛都要分出胜负,胜一场积3分,负
一场积1分.某班级在15场比赛中获得总积分为41分,问该班级
胜负场数分别是多少?
解:(1)设胜了x场,负了y场,
根据题意得解得
答:该班级胜负场数分别是13场和2场.
解:(1)设胜了x场,负了y场,
根据题意得解得
答:该班级胜负场数分别是13场和2场.
(2)投篮得分规则:在3分线外投篮,投中一球可得3分,在3分线内(含3分线)投篮,投中一球可得2分,某班级在其中一场比赛中,共投中26个球(只有2分球和3分球),所得总分不少于56分,问该班级这场比赛中至少投中了多少个3分球?
解:(2)设该班级这场比赛中投中了m个3分球,则投中了(26-m)个2分球.
根据题意得3m+2(26-m)≥56,
解得m≥4.
答:该班级这场比赛中至少投中了4个3分球.
10. (2023·长沙)为提升学生身体素质,落实教育部门“在校学生每天锻炼时间不少于1小时”的文件精神.某校利用课后服务时间,在八年级开展“体育赋能,助力成长”班级篮球赛,共16个班级参加.
课堂小结
一元一次不等式(组)
不等式的性质
一元一次不等式(组)的解法
不等式(组)的相关概念
一元一次不等式(组)的实际应用
第8讲 一元一次不等式(组)
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第二单元 第8讲
课标要求 作业目标
一元一次不等式 (组) 1.了解不等式的意义,探索不等式的基本性质. 2.能解数字系数的一元一次不等式,能根据具体问题中的数量关系,列出一元一次不等式,解决简单的问题. 能够说明一元一次不等式及其相关概念
识记解一元一次不等式的一般步骤,掌握一元一次不等式的解法
能够在数轴上表示出一元一次不等式的解集
了解不等式组及相关概念
会解由两个一元一次不等式组成的不等式组,并会用数轴确定解集
能根据实际问题中的数量关系,列出一元一次不等式(组),解决实际问题
根据方程和不等式的关系,整理归纳并解决综合问题
要求与目标
教材整合 核心归纳
02
第二单元 第8讲
不等式
的基本
性质 性质1:若a>b,则a±c b±c
性质2:若a>b,c>0,则ac bc,
性质3:若a>b,c<0,则ac bc,
>
>
>
<
<
考点 不等式的基本性质
考点清单
一元
一次 不等
式的 解法 一般步骤:去分母、去括号、移项、合并同类项、系数化为1
解集在数轴上表示:
x≥a
x>a
x≤a
x<a
考点 一元一次不等式(组)的解法【省卷T10】
考点清单
一元一次 不等式组 的解法 一般步骤:先分别解出每个一元一次不等式的解集,再求出它们解集的公共部分 解 集 在 数 轴 上 表 示 类型(a>b) 口诀 图示 解集
同大取大
x>a
同小取小
_________
小大大小取中间 __________
大大小小取不了 无解
考点 一元一次不等式(组)的解法【省卷T10】
x<b
b<x<a
考点清单
一般
步骤 审题、设未知数、找不等关系、列不等式、解不等式、检验是否符合实际、作答
关
键
词 实际问题中,出现至少、不低于、不小于(≥);最多、不高于、不大于(≤);大于、多于、超过、高于(>);少于、小于、不足、低于(<)等,一般利用不等式解题
考点 一元一次不等式的实际应用 省卷T23,长沙T22】
考点清单
重难精讲
变式探究
03
第二单元 第8讲
例1 解不等式组请结合题意解答本题
(每空只需填出最后结果).
解:解不等式①,得 ;解不等式②,得 .
把不等式①和②的解集在下面的数轴上表示出来:
所以原不等式组的解集为 .
x>-2
x≤3
-2<x≤3
例2 改编问题链 已知关于x的不等式组
(1)若该不等式组的解集为-1<x≤3,则a的值为 ;
(2)若该不等式组无解,则a的取值范围为 ;
-3
a≥1
(3)若该不等式组的整数解有3个,则a的取值范围为 .
-2≤a<-1
x>a+2
x≤3
a+2=-1
a=-3
大大小小取不了
a+2≥3
a≥1
3,2,1
0≤a+2<1
-2≤a<-1
易错1:在数轴上表示不等式(组)的解集时,“<”“>”的边
界点用空心点,“≤”“≥”的边界点用实心点.
易错2:含参问题中,求参数的取值范围时,要注意边界点是
否取等号.
1. (2024·上海)如果x>y,那么下列正确的是( C )
A. x+5≤y+5 B. x-5<y-5
C. 5x>5y D.-5x>-5y
2. 如下图,数轴上的两点A,B对应的实数分别是a,b,则
下列式子中成立的是( A )
A. 1-2a>1-2b B. -a<-b
C. a+b<0 D. |a|-|b|>0
第2题图
C
A
3. (2024·湖北)不等式 x+1≥2 的解集在数轴上表示正确的是
( A )
4. (2024·南充)若关于x的不等式组的解集为x<3,
则m的取值范围是( B )
A. m>0 B. m≥2
C. m<2 D. m≤2
A
B
x<3
同小取小
m+1≥3
m≥2
5. (2024·扬州)解不等式组并求出它的所有整数
解的和.
解:解不等式2x-6≤0,得x≤3.
解不等式x< ,得x> .
所以不等式组的解集为 <x≤3.
所以整数解为1,2,3,整数解的和为6.
解:解不等式2x-6≤0,得x≤3.
解不等式x< ,得x> .
所以不等式组的解集为 <x≤3.
所以整数解为1,2,3,整数解的和为6.
6. 某品牌护眼灯的进价为240元,商店以320元的价格出售.“五一”假日期间,商店为让利于顾客,计划以利润率不低于20%的价格降价出售,则该护眼灯最多可降价 元.
32
不等关系
利润率=利润÷进价×100%
设可降价 a 元
×100%≥20%
a ≤32
(1)求A种湘绣作品和B种湘绣作品的单价分别为多少元;
解:(1)设A种湘绣作品的单价为x元,
B种湘绣作品的单价为y元.
根据题意得解得
答:A种湘绣作品的单价为300元,
B种湘绣作品的单价为200元.
7. (2024·长沙)刺绣是我国民间传统手工艺,湘绣作为中国四大
刺绣之一,闻名中外.在巴黎奥运会倒计时50天之际,某国际
旅游公司计划购买A,B两种奥运主题的湘绣作品作为纪念品.
已知购买1件A种湘绣作品与2件B种湘绣作品共需要700元,
购买2件A种湘绣作品与3件B种湘绣作品共需要1200元.
(2)该国际旅游公司计划购买A种湘绣作品和B种湘绣作品共200件,总费用不超过50000元,那么最多能购买A种湘绣作品多少件?
解:(2)设购买A种湘绣作品m件,则购买B种湘绣作品(200-m)件.
根据题意得300m+200(200-m)≤50000,
解得m≤100.
∴m的最大值为100.
答:最多能购买A种湘绣作品100件.
7. (2024·长沙)刺绣是我国民间传统手工艺,湘绣作为中国四大刺绣之一,闻名中外.在巴黎奥运会倒计时50天之际,某国际旅游公司计划购买A,B两种奥运主题的湘绣作品作为纪念品.已知购买1件A种湘绣作品与2件B种湘绣作品共需要700元,购买2件A种湘绣作品与3件B种湘绣作品共需要1200元.
8. 关于x,y的方程组的解中x与y的和不
小于5,则k的取值范围为( A )
A. k≥8 B. k>8 C. k≤8 D. k<8
A
9. (2024·湖南)在平面直角坐标系xOy中,对于点P(x,y),若
x,y均为整数,则称点P为“整点”.特别地,当 (其中
xy≠0)的值为整数时,称“整点”P为“超整点”.已知点
P(2a-4,a+3)在第二象限,下列说法正确的是( C )
A. a<-3
B. 若点P为“整点”,则点P的个数为3个
C. 若点P为“超整点”,则点P的个数为1个
D. 若点P为“超整点”,则点P到两坐标轴的距离之和大于10
C
10. (2023·长沙)为提升学生身体素质,落实教育部门“在校学
生每天锻炼时间不少于1小时”的文件精神.某校利用课后服务
时间,在八年级开展“体育赋能,助力成长”班级篮球赛,共
16个班级参加.
(1)比赛积分规定:每场比赛都要分出胜负,胜一场积3分,负
一场积1分.某班级在15场比赛中获得总积分为41分,问该班级
胜负场数分别是多少?
解:(1)设胜了x场,负了y场,
根据题意得解得
答:该班级胜负场数分别是13场和2场.
解:(1)设胜了x场,负了y场,
根据题意得解得
答:该班级胜负场数分别是13场和2场.
(2)投篮得分规则:在3分线外投篮,投中一球可得3分,在3分线内(含3分线)投篮,投中一球可得2分,某班级在其中一场比赛中,共投中26个球(只有2分球和3分球),所得总分不少于56分,问该班级这场比赛中至少投中了多少个3分球?
解:(2)设该班级这场比赛中投中了m个3分球,则投中了(26-m)个2分球.
根据题意得3m+2(26-m)≥56,
解得m≥4.
答:该班级这场比赛中至少投中了4个3分球.
10. (2023·长沙)为提升学生身体素质,落实教育部门“在校学生每天锻炼时间不少于1小时”的文件精神.某校利用课后服务时间,在八年级开展“体育赋能,助力成长”班级篮球赛,共16个班级参加.
课堂小结
一元一次不等式(组)
不等式的性质
一元一次不等式(组)的解法
不等式(组)的相关概念
一元一次不等式(组)的实际应用
同课章节目录
