第10讲 一次函数的图象与性质 2025年中考一轮数学专题复习课件(湖南)(共28张PPT)
文档属性
| 名称 | 第10讲 一次函数的图象与性质 2025年中考一轮数学专题复习课件(湖南)(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
第10讲 一次函数的图象与性质
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第三单元 第10讲
课标要求 作业目标
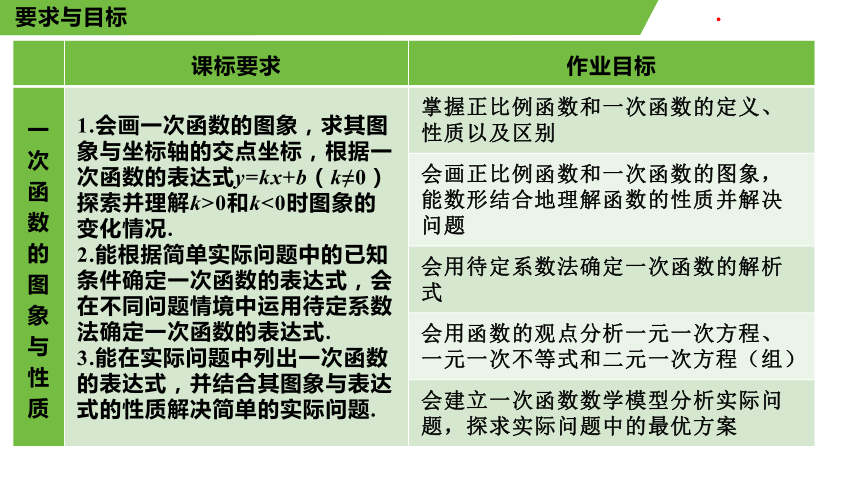
一次函数的图象与性质 1.会画一次函数的图象,求其图象与坐标轴的交点坐标,根据一次函数的表达式y=kx+b(k≠0)探索并理解k>0和k<0时图象的变化情况. 2.能根据简单实际问题中的已知条件确定一次函数的表达式,会在不同问题情境中运用待定系数法确定一次函数的表达式. 3.能在实际问题中列出一次函数的表达式,并结合其图象与表达式的性质解决简单的实际问题. 掌握正比例函数和一次函数的定义、性质以及区别
会画正比例函数和一次函数的图象,能数形结合地理解函数的性质并解决问题
会用待定系数法确定一次函数的解析式
会用函数的观点分析一元一次方程、一元一次不等式和二元一次方程(组)
会建立一次函数数学模型分析实际问题,探求实际问题中的最优方案
要求与目标
教材整合 核心归纳
02
第三单元 第10讲
1. (2024·上海)若正比例函数y=kx的图象经过点(7,-13),
则y的值随x的增大而 (选填“增大”或“减小”).
减小
2. 已知一组函数串M:①y=-2x+3;②y=2x-1;
③y=-2x+2;④y= x-1,将其分别填在下面考点对应的横线上.
点在第四象限
k<0
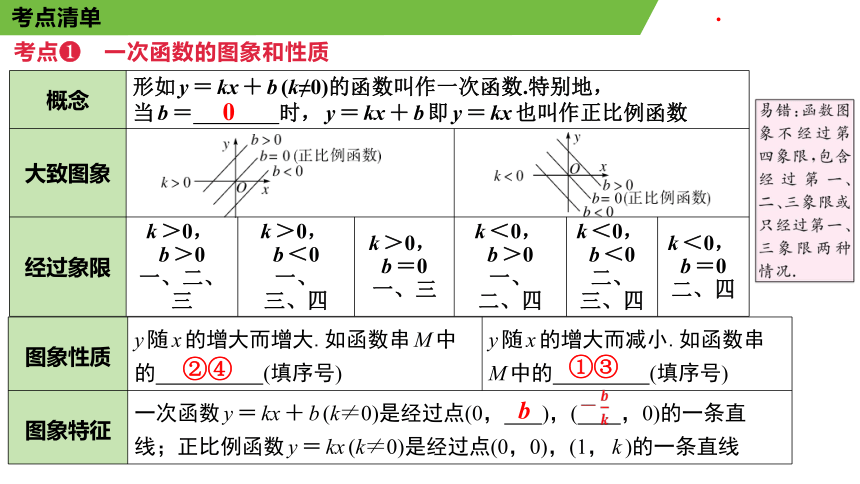
概念 形如y=kx+b(k≠0)的函数叫作一次函数.特别地, 当b= 时,y=kx+b即y=kx也叫作正比例函数 大致图象 经过象限 k>0,
b>0 一、二、三 k>0,
b<0 一、
三、四 k>0,
b=0 一、三 k<0,
b>0 一、
二、四 k<0,
b<0 二、
三、四 k<0,
b=0
二、四
0
图象性质 y随x的增大而增大.如函数串M中的 (填序号) y随x的增大而减小.如函数串M中的 (填序号)
图象特征 一次函数y=kx+b(k≠0)是经过点(0, ),( ,0)的一条直线;正比例函数y=kx(k≠0)是经过点(0,0),(1,k)的一条直线 ②④
①③
b
-
考点 一次函数的图象和性质
考点清单
待定系数
法的步骤 ①设:设所求一次函数解析式为y=kx+b(k≠0); ②列:将图象上两点坐标代入解析式,得到方程组; ③解:解关于k,b的方程组,求出k,b的值; ④定:将求得的k,b的值代入y=kx+b, 写出函数解析式 函数y=
kx+b图
象的平移 向左平移m个单位长度→y=k(x )+b; 向右平移m个单位长度→y=k(x )+b; 向上平移m个单位长度→y=kx+b ; 向下平移m个单位长度→y=kx+b . 如函数串M的图象中直线①可通
过直线 向 平移 个单位长度得到 口诀:
左加右减自变量,上加下减
常数项
+m
-m
+m
-m
③
上(或右)
1(或 )
考点 确定一次函数的解析式
考点清单
函数 y=kx+b(k>0) y=kx+b(k>0),y=k1x+b1(k1<0)
方程
(组) 方程kx+b=0的
解为
方程组 的解为
不等式 不等式kx+b>0 (或kx+b<0)的解集为x>x0(或x<x0) 不等式kx+b>k1x+b1(或kx+b
<k1x+b1)的解集为
x=x0
x>m(或x<m)
考点 一次函数与方程(组)、不等式的关系
考点清单
重难精讲
变式探究
03
第三单元 第10讲
例 原创问题链 如下图,将直线y= x向上平移1个单位长度得到直线l1:y=kx+b,直线l1分别与x轴、y轴交于点A,B.
直线l2:y=mx+n分别与x轴、y轴交于点C(8,0),D(0,6).两直线交于点E.
(1)求直线l1和直线l2的解析式;
解:(1)将直线y= x向上平移1个单位长度得到y= x+1,
∴直线l1的解析式为y= x+1.把C(8,0),D(0,6)代入
y=mx+n得解得
∴直线l2的解析式为y=- x+6.
例 原创问题链 如下图,将直线y= x向上平移1个单位长度得到直线l1:y=kx+b,直线l1分别与x轴、y轴交于点A,B. 直线l2:y=mx+n分别与x轴、y轴交于点C(8,0),D(0,6).两直线交于点E.
(2)对于直线l2:y=mx+n,当-3<x≤1时,y的取值范围
为 ;【易错】
≤y<
直线l2:y=- x+6.
当 x=1 时,y=
当 x=-3 时,y=
-3
1
易错:
①当一次函数中k<0时,y随x的增大而减小,当x取最大值时,y反而取最小值;
②当一次函数中无法判断k>0还是k<0时,需分情况讨论.
(3)根据图象直接写出不等式kx+b≥mx+n的解集: ;
x≥4
例 原创问题链 如下图,将直线y= x向上平移1个单位长度得到直线l1:y=kx+b,直线l1分别与x轴、y轴交于点A,B. 直线l2:y=mx+n分别与x轴、y轴交于点C(8,0),D(0,6).两直线交于点E.
直线 l1 在直线 l2 的上方
直线l1:y= x+1.
直线l2:y=- x+6.
联立
解得
求交点 E 的横坐标
x=4
(4)求△ADE的面积.【方法】
例 原创问题链 如下图,将直线y= x向上平移1个单位长度得到直线l1:y=kx+b,直线l1分别与x轴、y轴交于点A,B. 直线l2:y=mx+n分别与x轴、y轴交于点C(8,0),D(0,6).两直线交于点E.
方法:利用割补转化求面积:将所求图形的面积转化到含有与x轴或y轴平行的边的三角形中来解决.
路径②(铅垂法):
S△ADE=S△ABD+S△BDE= BD(xE-xA).
路径①:S△ADE=S△ADC-S△AEC;
解:(4)在y= x+1中,当x=0时,y=1,
当y=0时,x=-2.∴A(-2,0),B(0,1).
联立得∴E(4,3).
∴S△ADE= ×(6-1)×(4+2)=15.
(4)求△ADE的面积.【方法】
例 原创问题链 如下图,将直线y= x向上平移1个单位长度得到直线l1:y=kx+b,直线l1分别与x轴、y轴交于点A,B. 直线l2:y=mx+n分别与x轴、y轴交于点C(8,0),D(0,6).两直线交于点E.
方法归纳
解一元一次方程
一次函数当y=0时,求x的值
确定直线与x轴交点的横坐标
可转化为
从图象上看
解二元一次方程组
两条直线的交点
求一次函数图象的交点坐标
可转化为
从图象上看
解一元一次不等式或
一次函数求当y>0或y<0时,x的取值范围
当y>0时,直线上的点在x轴上方;y<0时,直线上的点在x轴下方
可转化为
从图象上看
解一元一次不等式
一次函数,求当时x的取值范围
以交点为界限,直线位于直线上方的那部分图象
可转化为
从图象上看
1. 下列函数图象中,表示直线y=2x+1的是( B )
B
2. (2024·长沙)对于一次函数y=2x-1,下列结论正确的是( )
A. 它的图象与y轴交于点(0,-1)
B. y随x的增大而减小
C. 当x> 时,y<0
D. 它的图象经过第一、二、三象限
A
当x=0时,y=-1
2>0,y随x的增大而增大
当x> 时,y>0
2>0,-1<0,过第一、三、四象限
3. 在平面直角坐标系中,已知点A(,m),点B(,n)是直
线y=kx+b(k<0)上的两点,则m,n的大小关系是( A )
A. m<n B. m>n
C. m≥n D. m≤n
A
4. 一次函数y=mx+m2(m≠0)的图象过点(0,4),且y随x的
增大而减小,则m的值为 .
-2
5. 将直线y=2x+1向上平移2个单位.
(1)平移后的直线对应的函数解析式是 .
(2)平移后的直线相当于将原直线( B )
A. 向左平移2个单位 B. 向左平移1个单位
C. 向右平移2个单位 D. 向右平移1个单位
y=2x+3
B
y=2x+3
y=2x+2+1
y=2(x+1)+1
口诀:左加右减自变量
6. 如下图,在平面直角坐标系中,矩形OABC的两个顶点坐标
为A(3,0),B(3,2).
第6题图
(1)对角线AC所在直线的函数解析式为 ;
y=- x+2
解:∵S△CAP= S△COA,
∴AP= OA=2.
∵A(3,0),∴P(1,0)或(5,0).
设直线CP的解析式为y=mx+2,
把P的坐标代入,得0=m+2或0=5m+2,
解得m=-2或m=- ,
∴直线CP所对应的函数解析式为y=-2x+2或y=- x+2.
解:∵S△CAP= S△COA,
∴AP= OA=2.
∵A(3,0),∴P(1,0)或(5,0).
设直线CP的解析式为y=mx+2,
把P的坐标代入,得0=m+2或0=5m+2,
解得m=-2或m=- ,
∴直线CP所对应的函数解析式为y=-2x+2或y=- x+2.
6. 如下图,在平面直角坐标系中,矩形OABC的两个顶点坐标
为A(3,0),B(3,2).
(2)若点P在x轴上,且S△CAP= S△COA,求直线CP所对应的函
数解析式.
第6题图
7. 如下图,直线y=x+b和y=kx+4与x轴分别相交于点A(-4,0),
B(2,0),则方程组的解为( C )
C
A. B.
C. D.
y=x+b
y=kx+4
4
8. 如上图,函数y=kx+b(k<0)的图象经过点P,则关于x的不等式kx+b>3的解集为 .
x<-1
第8题图
第7题图
9. (2024·南充)当2≤x≤5时,一次函数y=(m+1)x+m2+1有最大值6,
则实数m的值为( A )
A. -3或0 B. 0或1 C. -5或-3 D. -5或1
A
分析:当 m+1>0,即 m>-1 时,y 随 x 的增大而增大,
∴当 x=5 时,一次函数 y=(m+1)x+m +1 有最大值6.
∴5(m+1)+m +1=6,解得 m1=0,m2=-5(舍去).
当 m+1<0,即 m<-1 时,y 随 x 的增大而减小,
∴当 x=2 时,一次函数 y= (m+1)x+m +1有最大值6.
∴2(m+1)+m +1=6,解得 m1=-3,m2=1(舍去).
综上,当2≤x≤5时,一次函数 y=(m+1)x+m +1 有最大值6,则实数 m 的值为0或-3.
分类讨论
10. (2024·广安)如上图,直线y=2x+2与x轴、y轴分别相交于点A,B,将△AOB绕点A按逆时针方向旋转90°得到△ACD,则点D的坐标为 .
第10题图
(-3,1)
11. (2024·北京改编)在平面直角坐标系xOy中,函数y=kx+
b(k≠0)与y=-kx+3的图象交于点(2,1).
(1)求k,b的值;
解:(1)∵直线y=-kx+3过点(2,1),
∴-2k+3=1,解得k=1.
将点(2,1)代入y=x+b,
得2+b=1,解得b=-1.
综上所述,k=1,b=-1.
(2)当x>2时,对于x的每一个值,函数y=x+m的值既大于函
数y=kx+b的值,也大于函数y=-kx+3的值,直接写出m
的取值范围.
解:(2)m的取值范围是m>-1.
课堂小结
一次函数
一次函数(正比例函数)的图象与性质
一次函数图象的平移、对称和旋转
一次函数与方程(组)、不等式
待定系数法求解析式
第10讲 一次函数的图象与性质
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第三单元 第10讲
课标要求 作业目标
一次函数的图象与性质 1.会画一次函数的图象,求其图象与坐标轴的交点坐标,根据一次函数的表达式y=kx+b(k≠0)探索并理解k>0和k<0时图象的变化情况. 2.能根据简单实际问题中的已知条件确定一次函数的表达式,会在不同问题情境中运用待定系数法确定一次函数的表达式. 3.能在实际问题中列出一次函数的表达式,并结合其图象与表达式的性质解决简单的实际问题. 掌握正比例函数和一次函数的定义、性质以及区别
会画正比例函数和一次函数的图象,能数形结合地理解函数的性质并解决问题
会用待定系数法确定一次函数的解析式
会用函数的观点分析一元一次方程、一元一次不等式和二元一次方程(组)
会建立一次函数数学模型分析实际问题,探求实际问题中的最优方案
要求与目标
教材整合 核心归纳
02
第三单元 第10讲
1. (2024·上海)若正比例函数y=kx的图象经过点(7,-13),
则y的值随x的增大而 (选填“增大”或“减小”).
减小
2. 已知一组函数串M:①y=-2x+3;②y=2x-1;
③y=-2x+2;④y= x-1,将其分别填在下面考点对应的横线上.
点在第四象限
k<0
概念 形如y=kx+b(k≠0)的函数叫作一次函数.特别地, 当b= 时,y=kx+b即y=kx也叫作正比例函数 大致图象 经过象限 k>0,
b>0 一、二、三 k>0,
b<0 一、
三、四 k>0,
b=0 一、三 k<0,
b>0 一、
二、四 k<0,
b<0 二、
三、四 k<0,
b=0
二、四
0
图象性质 y随x的增大而增大.如函数串M中的 (填序号) y随x的增大而减小.如函数串M中的 (填序号)
图象特征 一次函数y=kx+b(k≠0)是经过点(0, ),( ,0)的一条直线;正比例函数y=kx(k≠0)是经过点(0,0),(1,k)的一条直线 ②④
①③
b
-
考点 一次函数的图象和性质
考点清单
待定系数
法的步骤 ①设:设所求一次函数解析式为y=kx+b(k≠0); ②列:将图象上两点坐标代入解析式,得到方程组; ③解:解关于k,b的方程组,求出k,b的值; ④定:将求得的k,b的值代入y=kx+b, 写出函数解析式 函数y=
kx+b图
象的平移 向左平移m个单位长度→y=k(x )+b; 向右平移m个单位长度→y=k(x )+b; 向上平移m个单位长度→y=kx+b ; 向下平移m个单位长度→y=kx+b . 如函数串M的图象中直线①可通
过直线 向 平移 个单位长度得到 口诀:
左加右减自变量,上加下减
常数项
+m
-m
+m
-m
③
上(或右)
1(或 )
考点 确定一次函数的解析式
考点清单
函数 y=kx+b(k>0) y=kx+b(k>0),y=k1x+b1(k1<0)
方程
(组) 方程kx+b=0的
解为
方程组 的解为
不等式 不等式kx+b>0 (或kx+b<0)的解集为x>x0(或x<x0) 不等式kx+b>k1x+b1(或kx+b
<k1x+b1)的解集为
x=x0
x>m(或x<m)
考点 一次函数与方程(组)、不等式的关系
考点清单
重难精讲
变式探究
03
第三单元 第10讲
例 原创问题链 如下图,将直线y= x向上平移1个单位长度得到直线l1:y=kx+b,直线l1分别与x轴、y轴交于点A,B.
直线l2:y=mx+n分别与x轴、y轴交于点C(8,0),D(0,6).两直线交于点E.
(1)求直线l1和直线l2的解析式;
解:(1)将直线y= x向上平移1个单位长度得到y= x+1,
∴直线l1的解析式为y= x+1.把C(8,0),D(0,6)代入
y=mx+n得解得
∴直线l2的解析式为y=- x+6.
例 原创问题链 如下图,将直线y= x向上平移1个单位长度得到直线l1:y=kx+b,直线l1分别与x轴、y轴交于点A,B. 直线l2:y=mx+n分别与x轴、y轴交于点C(8,0),D(0,6).两直线交于点E.
(2)对于直线l2:y=mx+n,当-3<x≤1时,y的取值范围
为 ;【易错】
≤y<
直线l2:y=- x+6.
当 x=1 时,y=
当 x=-3 时,y=
-3
1
易错:
①当一次函数中k<0时,y随x的增大而减小,当x取最大值时,y反而取最小值;
②当一次函数中无法判断k>0还是k<0时,需分情况讨论.
(3)根据图象直接写出不等式kx+b≥mx+n的解集: ;
x≥4
例 原创问题链 如下图,将直线y= x向上平移1个单位长度得到直线l1:y=kx+b,直线l1分别与x轴、y轴交于点A,B. 直线l2:y=mx+n分别与x轴、y轴交于点C(8,0),D(0,6).两直线交于点E.
直线 l1 在直线 l2 的上方
直线l1:y= x+1.
直线l2:y=- x+6.
联立
解得
求交点 E 的横坐标
x=4
(4)求△ADE的面积.【方法】
例 原创问题链 如下图,将直线y= x向上平移1个单位长度得到直线l1:y=kx+b,直线l1分别与x轴、y轴交于点A,B. 直线l2:y=mx+n分别与x轴、y轴交于点C(8,0),D(0,6).两直线交于点E.
方法:利用割补转化求面积:将所求图形的面积转化到含有与x轴或y轴平行的边的三角形中来解决.
路径②(铅垂法):
S△ADE=S△ABD+S△BDE= BD(xE-xA).
路径①:S△ADE=S△ADC-S△AEC;
解:(4)在y= x+1中,当x=0时,y=1,
当y=0时,x=-2.∴A(-2,0),B(0,1).
联立得∴E(4,3).
∴S△ADE= ×(6-1)×(4+2)=15.
(4)求△ADE的面积.【方法】
例 原创问题链 如下图,将直线y= x向上平移1个单位长度得到直线l1:y=kx+b,直线l1分别与x轴、y轴交于点A,B. 直线l2:y=mx+n分别与x轴、y轴交于点C(8,0),D(0,6).两直线交于点E.
方法归纳
解一元一次方程
一次函数当y=0时,求x的值
确定直线与x轴交点的横坐标
可转化为
从图象上看
解二元一次方程组
两条直线的交点
求一次函数图象的交点坐标
可转化为
从图象上看
解一元一次不等式或
一次函数求当y>0或y<0时,x的取值范围
当y>0时,直线上的点在x轴上方;y<0时,直线上的点在x轴下方
可转化为
从图象上看
解一元一次不等式
一次函数,求当时x的取值范围
以交点为界限,直线位于直线上方的那部分图象
可转化为
从图象上看
1. 下列函数图象中,表示直线y=2x+1的是( B )
B
2. (2024·长沙)对于一次函数y=2x-1,下列结论正确的是( )
A. 它的图象与y轴交于点(0,-1)
B. y随x的增大而减小
C. 当x> 时,y<0
D. 它的图象经过第一、二、三象限
A
当x=0时,y=-1
2>0,y随x的增大而增大
当x> 时,y>0
2>0,-1<0,过第一、三、四象限
3. 在平面直角坐标系中,已知点A(,m),点B(,n)是直
线y=kx+b(k<0)上的两点,则m,n的大小关系是( A )
A. m<n B. m>n
C. m≥n D. m≤n
A
4. 一次函数y=mx+m2(m≠0)的图象过点(0,4),且y随x的
增大而减小,则m的值为 .
-2
5. 将直线y=2x+1向上平移2个单位.
(1)平移后的直线对应的函数解析式是 .
(2)平移后的直线相当于将原直线( B )
A. 向左平移2个单位 B. 向左平移1个单位
C. 向右平移2个单位 D. 向右平移1个单位
y=2x+3
B
y=2x+3
y=2x+2+1
y=2(x+1)+1
口诀:左加右减自变量
6. 如下图,在平面直角坐标系中,矩形OABC的两个顶点坐标
为A(3,0),B(3,2).
第6题图
(1)对角线AC所在直线的函数解析式为 ;
y=- x+2
解:∵S△CAP= S△COA,
∴AP= OA=2.
∵A(3,0),∴P(1,0)或(5,0).
设直线CP的解析式为y=mx+2,
把P的坐标代入,得0=m+2或0=5m+2,
解得m=-2或m=- ,
∴直线CP所对应的函数解析式为y=-2x+2或y=- x+2.
解:∵S△CAP= S△COA,
∴AP= OA=2.
∵A(3,0),∴P(1,0)或(5,0).
设直线CP的解析式为y=mx+2,
把P的坐标代入,得0=m+2或0=5m+2,
解得m=-2或m=- ,
∴直线CP所对应的函数解析式为y=-2x+2或y=- x+2.
6. 如下图,在平面直角坐标系中,矩形OABC的两个顶点坐标
为A(3,0),B(3,2).
(2)若点P在x轴上,且S△CAP= S△COA,求直线CP所对应的函
数解析式.
第6题图
7. 如下图,直线y=x+b和y=kx+4与x轴分别相交于点A(-4,0),
B(2,0),则方程组的解为( C )
C
A. B.
C. D.
y=x+b
y=kx+4
4
8. 如上图,函数y=kx+b(k<0)的图象经过点P,则关于x的不等式kx+b>3的解集为 .
x<-1
第8题图
第7题图
9. (2024·南充)当2≤x≤5时,一次函数y=(m+1)x+m2+1有最大值6,
则实数m的值为( A )
A. -3或0 B. 0或1 C. -5或-3 D. -5或1
A
分析:当 m+1>0,即 m>-1 时,y 随 x 的增大而增大,
∴当 x=5 时,一次函数 y=(m+1)x+m +1 有最大值6.
∴5(m+1)+m +1=6,解得 m1=0,m2=-5(舍去).
当 m+1<0,即 m<-1 时,y 随 x 的增大而减小,
∴当 x=2 时,一次函数 y= (m+1)x+m +1有最大值6.
∴2(m+1)+m +1=6,解得 m1=-3,m2=1(舍去).
综上,当2≤x≤5时,一次函数 y=(m+1)x+m +1 有最大值6,则实数 m 的值为0或-3.
分类讨论
10. (2024·广安)如上图,直线y=2x+2与x轴、y轴分别相交于点A,B,将△AOB绕点A按逆时针方向旋转90°得到△ACD,则点D的坐标为 .
第10题图
(-3,1)
11. (2024·北京改编)在平面直角坐标系xOy中,函数y=kx+
b(k≠0)与y=-kx+3的图象交于点(2,1).
(1)求k,b的值;
解:(1)∵直线y=-kx+3过点(2,1),
∴-2k+3=1,解得k=1.
将点(2,1)代入y=x+b,
得2+b=1,解得b=-1.
综上所述,k=1,b=-1.
(2)当x>2时,对于x的每一个值,函数y=x+m的值既大于函
数y=kx+b的值,也大于函数y=-kx+3的值,直接写出m
的取值范围.
解:(2)m的取值范围是m>-1.
课堂小结
一次函数
一次函数(正比例函数)的图象与性质
一次函数图象的平移、对称和旋转
一次函数与方程(组)、不等式
待定系数法求解析式
同课章节目录
