第12讲 反比例函数 2025年中考一轮数学专题复习课件(湖南)(共23张PPT)
文档属性
| 名称 | 第12讲 反比例函数 2025年中考一轮数学专题复习课件(湖南)(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
第12讲 反比例函数
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第三单元 第12讲
课标要求 作业目标
反比例函数 1.会用描点法画出反比例函数的图象,知道当k>0或k<0时反比例函数图象的整体特征. 2.结合具体情境用实例体会反比例函数的意义,能确定反比例函数的表达式. 3.能用反比例函数解决简单的实际问题. 认识反比例函数的概念,能够根据已知条件确定反比例函数的解析式.会根据反比例函数的解析式和自变量的值,求函数值
会根据解析式画反比例函数的图象,归纳得到反比例函数的图象特征和性质
理解和掌握反比例函数的图象和性质
运用反比例函数的图象和性质解决问题.领会反比例函数的解析式与图象之间的联系,体会数形结合及转化的思想方法
运用反比例函数的知识解决简单的实际问题.经历“实际问题-建立模型-拓展应用”的过程,发展分析、解决问题的能力
要求与目标
教材整合 核心归纳
02
第三单元 第12讲
已知反比例函数y= ,
①图象位于第 象限;
②图象所在的每个象限内,y随x的增大而 ;
一、三
减小
第三象限
④若图象经过点(a,a+2),则a= .
第一象限
<
③图象上的三点(-1,y1),(1,y2),(2,y3),
则y1,y2,y3的大小关系是 (用“>”连接);
y2>y3>y1
-3或1
y2>y3
>y1
反比例函数的概念 定义:形如y= (k是常数,k≠0)的函数,自变量x的取值范围为一切非零实数. 常见形式:①y= ;②y=kx-1;③xy=k(k是常数,k≠0) 大致图象
所在象限 第一、三象限(x,y同号) 第二、四象限(x,y异号)
图象特征 图象无限接近坐标轴,但与坐标轴永不相交 性质 增减性 在每一个象限内,y随x的增大而 在每一个象限内,y随x的增大而
对称性 ①图象关于直线y=x和y=-x成轴对称; ②图象关于 成中心对称 减小
增大
原点O
提醒:利用反比例函数图象的增减性时,点必须在同一分支上.
考点 反比例函数的图象与性质
考点清单
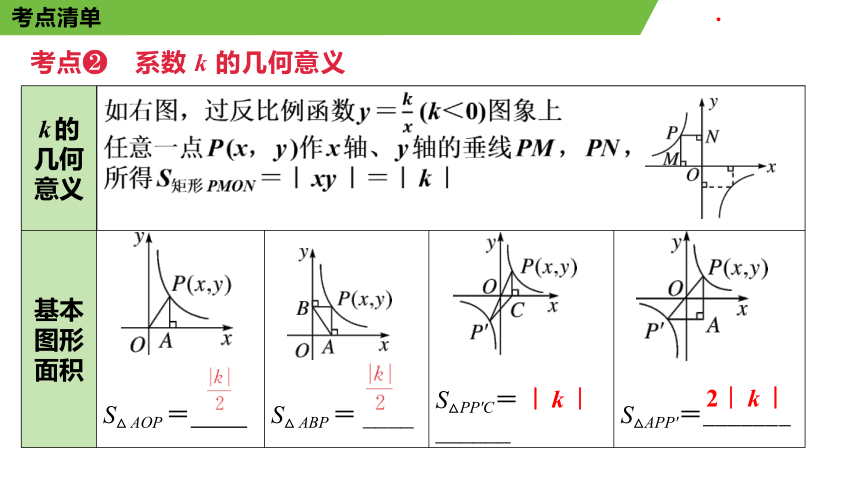
k的几何意义 如右图,过反比例函数y= (k<0)图象上 任意一点P(x,y)作x轴、y轴的垂线PM,PN, 所得S矩形PMON=|xy|=|k| 基本图形面积
S△AOP=.____
S△ABP= ____ S△PP'C=______
S△APP'=_______
|k|
2|k|
考点 系数 k 的几何意义
考点清单
待定系
数法 ①设反比例函数的解析式为y= (k≠0);
②找出反比例函数图象上的任意一点
P(a,b),代入解析式,得k=ab;
③确定解析式为y=
几何法 题中涉及面积时,考虑根据k的几何意义求解,由面积得|k|,再根据函数所在象限得出k
考点 反比例函数解析式的确定【长沙T10】
考点清单
重难精讲
变式探究
03
第三单元 第12讲
例 原创问题链 已知一次函数y=k1x+b的图象与反比例函数y= 的图象交于A(-4,1),B(m,4) 两点(k1,k2,b为常数).
(1)求一次函数和反比例函数的解析式,并在下面的坐标系中画出两函数图象的草图;
解:(1) 将点 A(-4,1) 代入y= ,得k2=-4.
∴反比例函数的解析式为y=- .
将B(m,4)代入反比例函数y=- ,得m=-1,
将点A(-4,1),B(-1,4)代入y=k1x+b,得
解得
∴一次函数的解析式为y=x+5.
画出两函数图象的草图如图所示.
∴点B的坐标为(-1,4).
(2) 根据图象直接写出不等式 >k1x+b
的解集: ;
(3)若点(-1,y1),(3,y2),(5,y3)在反比例函数图象上,则y1,y2,y3的大小关系为
(用“>”连接);
x<-4或-1<x<0
y1>y3>y2
(4)【k的几何意义】若点D为反比例函数图象上的一点,
作DE⊥x轴于点E,点F为y轴上任意一点,则S△DEF= ;
2
反比例函数的解析式为y=- .
一次函数的解析式为y=x+5.
反比例函数在一次函数上方
O
x
y
B
A
C
-4
-1
①第二象限>第四象限;
②在每个象限内,y随x的增大而增大
D
E
F
S△DEF= |k|=2
(5)【割补法·分类讨论思想】点P为y轴上一点,若△PAB的面积为3,求点P的坐标.
解:(5) 如图,设一次函数的图象与y轴交于点C,
则C(0,5).
设P(0,t),则PC=|t-5|.
∴S△PAB=S△APC-S△BPC
= ×4×|t-5|- ×1×|t-5|=3,
解得t=3或t=7.
∴点P的坐标为(0,3)或(0,7).
反比例函数的解析式为y=- .
一次函数的解析式为y=x+5.
O
x
y
B
A
C
P
路径:S△APB=S△APC-S△PBC
1. (2023·株洲)下列各点在反比例函数y= 的图象上的是( )
A. P1(1,-4) B. P2(4,-1)
C. P3(2,4) D. P4(2 , )
D
2. 一次函数 y=kx+1 和反比例函数y= 在同一坐标系中的
大致图象是( D )
D
过点(0,1)
一次函数:k<0
反比例函数:k>0
3. (2024·陕西)已知点A(-2,y1)和点B(m,y2)均在反比例函
数y=- 的图象上.若0<m<1,则y1+y2 0(填“>”
“=”或“<”).
<
y2<-5
y1=
y1+y2<-5+
y1+y2<-
O
x
y
1
-5
4. 如下图,直线AB交x轴于点C,交反比例函数y= (a>1)
的图象于A,B两点,过点B作BD⊥y轴,垂足为点D,若
S△BCD=5,则a的值为( D )
A. 8 B. 9 C. 10 D. 11
第4题图
D
S△BCD=×| k|=×| a-1|=5
a=11
a>1
5. (2024·齐齐哈尔)如上图,反比例函数y= (x<0)的图象经过平行四边形ABCO的顶点A,OC在x轴上,若点B(-1,3),S ABCO=3,则实数k的值为 .
第5题图
-6
【变式题】如上图,点A在反比例函数y= (k≠0)图象的一支上,点B在反比例函数y=- 图象的一支上,点C,D在x轴上.若四边形ABCD是面积为9的矩形,则实数k的值为 .
-6
变式题图
AB×| yB|=3
AB=1
3
-1
xA=-2
-2
k=-6
6. (2024·湖南)在一定条件下,乐器中弦振动的频率f与弦长l成
反比例关系,即f= (k为常数,k≠0).若某乐器的弦长l为0.9
米,振动频率f为200赫兹,则k的值为 .
7. 根据物理学知识,在压力不变的情况下,某物体承受的压
强p(Pa)是它的受力面积S(m2)的反比例函数,其函数图象如下
图所示.当S=0.25m2时,该物体承受的压强p的值
为 Pa.
180
400
第7题图
8. (2024·长沙)如下图,在菱形ABCD中,AB=6,∠B=
30°,点E是BC边上的动点,连接AE,DE,过点A作
AF⊥DE于点F. 设DE=x,AF=y,则y与x之间的函数解析
式为(不考虑自变量x的取值范围)( C )
A. y= B. y=
C. y= D. y=
第8题图
C
9. 【参数法】如上图,在矩形OABC和正方形CDEF中,点A在y轴正半轴上,点C,F均在x轴正半轴上,点D在边BC上,BC=2CD,AB=3.若点B,E在同一个反比例函数的图象上,则这个反比例函数的表达式是 .
第9题图
思路点拨:设正方形的边长为a,作ED的延长线交OA于点G. 根据S矩形OABC=S矩形OFEG可得出结果.
y=
10. (2024·包头)若反比例函数y1= ,y2=- ,当1≤x≤3时,函数y1的最大值是a,函数y2的最大值是b,则ab= .
(1)求这个反比例函数的表达式;
(2)请先描出这个反比例函数图象上不同于点A的三个格点,再画出反比例函数的图象;
解:(1)∵反比例函数y= 的图象经过点A(3,2),
∴2= .
∴k=6.
∴这个反比例函数的表达式为y= (x>0).
11. (2024·河南)如下图,矩形ABCD的四个顶点都在格点(网格线的交点)上,对角线AC,BD相交于点E,反比例函数y= (x>0)的图象经过点A.
解:(2)当x=1时,y=6;
当x=2时,y=3;
当x=6时,y=1.
∴反比例函数y= (x>0)的图象经过(1,6),(2,3),(6,1),
画图如上图所示.
(3)将矩形ABCD向左平移,当点E落在这个反比例函数的图象
上时,平移的距离为 .
11. (2024·河南)如下图,矩形ABCD的四个顶点都在格点(网格线的交点)上,对角线AC,BD相交于点E,反比例函数y=
(x>0)的图象经过点A.
课堂小结
反比例函数
反比例函数解析式的确定
反比例函数的图象与性质
反比例函数中系数k的几何意义
待定系数法
利用 k 的几何意义
第12讲 反比例函数
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第三单元 第12讲
课标要求 作业目标
反比例函数 1.会用描点法画出反比例函数的图象,知道当k>0或k<0时反比例函数图象的整体特征. 2.结合具体情境用实例体会反比例函数的意义,能确定反比例函数的表达式. 3.能用反比例函数解决简单的实际问题. 认识反比例函数的概念,能够根据已知条件确定反比例函数的解析式.会根据反比例函数的解析式和自变量的值,求函数值
会根据解析式画反比例函数的图象,归纳得到反比例函数的图象特征和性质
理解和掌握反比例函数的图象和性质
运用反比例函数的图象和性质解决问题.领会反比例函数的解析式与图象之间的联系,体会数形结合及转化的思想方法
运用反比例函数的知识解决简单的实际问题.经历“实际问题-建立模型-拓展应用”的过程,发展分析、解决问题的能力
要求与目标
教材整合 核心归纳
02
第三单元 第12讲
已知反比例函数y= ,
①图象位于第 象限;
②图象所在的每个象限内,y随x的增大而 ;
一、三
减小
第三象限
④若图象经过点(a,a+2),则a= .
第一象限
<
③图象上的三点(-1,y1),(1,y2),(2,y3),
则y1,y2,y3的大小关系是 (用“>”连接);
y2>y3>y1
-3或1
y2>y3
>y1
反比例函数的概念 定义:形如y= (k是常数,k≠0)的函数,自变量x的取值范围为一切非零实数. 常见形式:①y= ;②y=kx-1;③xy=k(k是常数,k≠0) 大致图象
所在象限 第一、三象限(x,y同号) 第二、四象限(x,y异号)
图象特征 图象无限接近坐标轴,但与坐标轴永不相交 性质 增减性 在每一个象限内,y随x的增大而 在每一个象限内,y随x的增大而
对称性 ①图象关于直线y=x和y=-x成轴对称; ②图象关于 成中心对称 减小
增大
原点O
提醒:利用反比例函数图象的增减性时,点必须在同一分支上.
考点 反比例函数的图象与性质
考点清单
k的几何意义 如右图,过反比例函数y= (k<0)图象上 任意一点P(x,y)作x轴、y轴的垂线PM,PN, 所得S矩形PMON=|xy|=|k| 基本图形面积
S△AOP=.____
S△ABP= ____ S△PP'C=______
S△APP'=_______
|k|
2|k|
考点 系数 k 的几何意义
考点清单
待定系
数法 ①设反比例函数的解析式为y= (k≠0);
②找出反比例函数图象上的任意一点
P(a,b),代入解析式,得k=ab;
③确定解析式为y=
几何法 题中涉及面积时,考虑根据k的几何意义求解,由面积得|k|,再根据函数所在象限得出k
考点 反比例函数解析式的确定【长沙T10】
考点清单
重难精讲
变式探究
03
第三单元 第12讲
例 原创问题链 已知一次函数y=k1x+b的图象与反比例函数y= 的图象交于A(-4,1),B(m,4) 两点(k1,k2,b为常数).
(1)求一次函数和反比例函数的解析式,并在下面的坐标系中画出两函数图象的草图;
解:(1) 将点 A(-4,1) 代入y= ,得k2=-4.
∴反比例函数的解析式为y=- .
将B(m,4)代入反比例函数y=- ,得m=-1,
将点A(-4,1),B(-1,4)代入y=k1x+b,得
解得
∴一次函数的解析式为y=x+5.
画出两函数图象的草图如图所示.
∴点B的坐标为(-1,4).
(2) 根据图象直接写出不等式 >k1x+b
的解集: ;
(3)若点(-1,y1),(3,y2),(5,y3)在反比例函数图象上,则y1,y2,y3的大小关系为
(用“>”连接);
x<-4或-1<x<0
y1>y3>y2
(4)【k的几何意义】若点D为反比例函数图象上的一点,
作DE⊥x轴于点E,点F为y轴上任意一点,则S△DEF= ;
2
反比例函数的解析式为y=- .
一次函数的解析式为y=x+5.
反比例函数在一次函数上方
O
x
y
B
A
C
-4
-1
①第二象限>第四象限;
②在每个象限内,y随x的增大而增大
D
E
F
S△DEF= |k|=2
(5)【割补法·分类讨论思想】点P为y轴上一点,若△PAB的面积为3,求点P的坐标.
解:(5) 如图,设一次函数的图象与y轴交于点C,
则C(0,5).
设P(0,t),则PC=|t-5|.
∴S△PAB=S△APC-S△BPC
= ×4×|t-5|- ×1×|t-5|=3,
解得t=3或t=7.
∴点P的坐标为(0,3)或(0,7).
反比例函数的解析式为y=- .
一次函数的解析式为y=x+5.
O
x
y
B
A
C
P
路径:S△APB=S△APC-S△PBC
1. (2023·株洲)下列各点在反比例函数y= 的图象上的是( )
A. P1(1,-4) B. P2(4,-1)
C. P3(2,4) D. P4(2 , )
D
2. 一次函数 y=kx+1 和反比例函数y= 在同一坐标系中的
大致图象是( D )
D
过点(0,1)
一次函数:k<0
反比例函数:k>0
3. (2024·陕西)已知点A(-2,y1)和点B(m,y2)均在反比例函
数y=- 的图象上.若0<m<1,则y1+y2 0(填“>”
“=”或“<”).
<
y2<-5
y1=
y1+y2<-5+
y1+y2<-
O
x
y
1
-5
4. 如下图,直线AB交x轴于点C,交反比例函数y= (a>1)
的图象于A,B两点,过点B作BD⊥y轴,垂足为点D,若
S△BCD=5,则a的值为( D )
A. 8 B. 9 C. 10 D. 11
第4题图
D
S△BCD=×| k|=×| a-1|=5
a=11
a>1
5. (2024·齐齐哈尔)如上图,反比例函数y= (x<0)的图象经过平行四边形ABCO的顶点A,OC在x轴上,若点B(-1,3),S ABCO=3,则实数k的值为 .
第5题图
-6
【变式题】如上图,点A在反比例函数y= (k≠0)图象的一支上,点B在反比例函数y=- 图象的一支上,点C,D在x轴上.若四边形ABCD是面积为9的矩形,则实数k的值为 .
-6
变式题图
AB×| yB|=3
AB=1
3
-1
xA=-2
-2
k=-6
6. (2024·湖南)在一定条件下,乐器中弦振动的频率f与弦长l成
反比例关系,即f= (k为常数,k≠0).若某乐器的弦长l为0.9
米,振动频率f为200赫兹,则k的值为 .
7. 根据物理学知识,在压力不变的情况下,某物体承受的压
强p(Pa)是它的受力面积S(m2)的反比例函数,其函数图象如下
图所示.当S=0.25m2时,该物体承受的压强p的值
为 Pa.
180
400
第7题图
8. (2024·长沙)如下图,在菱形ABCD中,AB=6,∠B=
30°,点E是BC边上的动点,连接AE,DE,过点A作
AF⊥DE于点F. 设DE=x,AF=y,则y与x之间的函数解析
式为(不考虑自变量x的取值范围)( C )
A. y= B. y=
C. y= D. y=
第8题图
C
9. 【参数法】如上图,在矩形OABC和正方形CDEF中,点A在y轴正半轴上,点C,F均在x轴正半轴上,点D在边BC上,BC=2CD,AB=3.若点B,E在同一个反比例函数的图象上,则这个反比例函数的表达式是 .
第9题图
思路点拨:设正方形的边长为a,作ED的延长线交OA于点G. 根据S矩形OABC=S矩形OFEG可得出结果.
y=
10. (2024·包头)若反比例函数y1= ,y2=- ,当1≤x≤3时,函数y1的最大值是a,函数y2的最大值是b,则ab= .
(1)求这个反比例函数的表达式;
(2)请先描出这个反比例函数图象上不同于点A的三个格点,再画出反比例函数的图象;
解:(1)∵反比例函数y= 的图象经过点A(3,2),
∴2= .
∴k=6.
∴这个反比例函数的表达式为y= (x>0).
11. (2024·河南)如下图,矩形ABCD的四个顶点都在格点(网格线的交点)上,对角线AC,BD相交于点E,反比例函数y= (x>0)的图象经过点A.
解:(2)当x=1时,y=6;
当x=2时,y=3;
当x=6时,y=1.
∴反比例函数y= (x>0)的图象经过(1,6),(2,3),(6,1),
画图如上图所示.
(3)将矩形ABCD向左平移,当点E落在这个反比例函数的图象
上时,平移的距离为 .
11. (2024·河南)如下图,矩形ABCD的四个顶点都在格点(网格线的交点)上,对角线AC,BD相交于点E,反比例函数y=
(x>0)的图象经过点A.
课堂小结
反比例函数
反比例函数解析式的确定
反比例函数的图象与性质
反比例函数中系数k的几何意义
待定系数法
利用 k 的几何意义
同课章节目录
