第15讲 图形初步与相交线、平行线 2025年中考一轮数学专题复习课件(湖南)(共20张PPT)
文档属性
| 名称 | 第15讲 图形初步与相交线、平行线 2025年中考一轮数学专题复习课件(湖南)(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 687.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 21:39:48 | ||
图片预览








文档简介
(共20张PPT)
第15讲
图形初步与相交线、平行线
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第四单元 第15讲
课标要求 作业目标
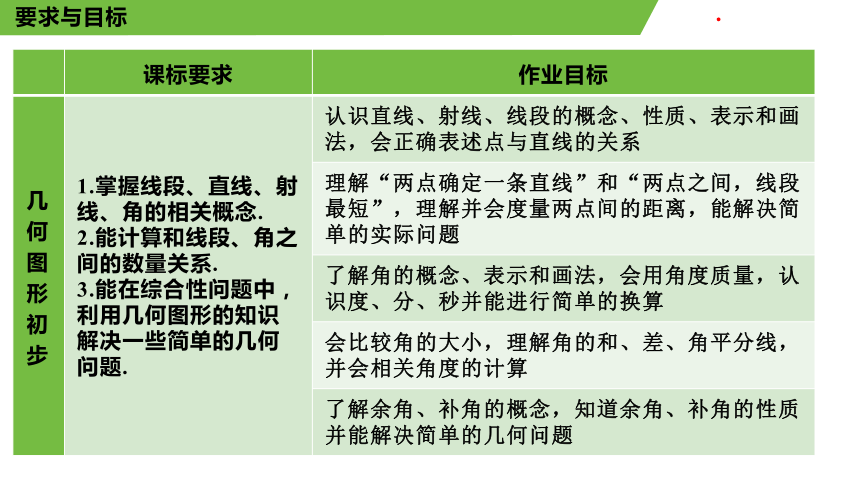
几何图形初步 1.掌握线段、直线、射线、角的相关概念. 2.能计算和线段、角之间的数量关系. 3.能在综合性问题中,利用几何图形的知识解决一些简单的几何问题. 认识直线、射线、线段的概念、性质、表示和画法,会正确表述点与直线的关系
理解“两点确定一条直线”和“两点之间,线段最短”,理解并会度量两点间的距离,能解决简单的实际问题
了解角的概念、表示和画法,会用角度质量,认识度、分、秒并能进行简单的换算
会比较角的大小,理解角的和、差、角平分线,并会相关角度的计算
了解余角、补角的概念,知道余角、补角的性质并能解决简单的几何问题
要求与目标
课标要求 作业目标
相交线与平行线 1.理解对顶角、余角、补角等概念,探索并掌握对顶角相等、同角(或等角)的余角相等、同角(或等角)的补角相等的性质。 2.理解垂线、垂线段等概念,能用三角板或量角器过一点画已知直线的垂线。 3.掌握基本事实:同一平面内,过一点有且只有一条直线与已知直线垂直。 4.理解点到直线的距离的意义,能度量点到直线的距离。 5.识别同位角、内错角、同旁内角。 6.理解平行线的概念。掌握平行线基本事实I:过直线外一点有且只有一条直线与这条直线平行。 知道对顶角、互补角的概念,掌握对顶角相等、邻补角互补的性质
知道垂线、垂线段等概念,掌握垂线段最短的性质
了解点到直线的距离的意义,能解释基本事实:过一点有且只有一条直线与已知直线垂直
识别同位角、内错角、同旁内角
了解平行线概念,能解释平行公理及相关结论
掌握判定两条直线平行的三种方法及两条平行线的三个性质
要求与目标
接下表
课标要求 作业目标
相交线与平行线 7.掌握平行线基本事实ⅡI:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。 8.探索并证明平行线的判定定理:两条直线被第三条直线所截, 如果内错角相等(或同旁内角互补),那么这两条直线平行。 9.掌握平行线的性质定理I:两条平行直线被第三条直线所截,同位角相等。 10.探索并证明平行线的性质定理ⅡI:两条平行直线被第三条直线所截,内错角相等(或同旁内角互补)。 11.了解平行于同一条直线的两条直线平行 知道对顶角、互补角的概念,掌握对顶角相等、邻补角互补的性质
知道垂线、垂线段等概念,掌握垂线段最短的性质
了解点到直线的距离的意义,能解释基本事实:过一点有且只有一条直线与已知直线垂直
识别同位角、内错角、同旁内角
了解平行线概念,能解释平行公理及相关结论
掌握判定两条直线平行的三种方法及两条平行线的三个性质
要求与目标
接上表
教材整合 核心归纳
02
第四单元 第15讲
1. (2024·广西改编)已知∠1=35°,若∠1与∠2为对顶角,则
∠2= °;若∠1与∠3互补,则∠3= °.
2. (2024·甘孜州)如右图,已知AB∥CD,AD平分∠BAC,
∠1=30°,则∠2的度数是 .
35
145
30°
∠1=∠3=30°
3
∠2=∠3=30°
两个基 本事实 (1)两点确定一条直线; (2)两点之间,线段最短.如右图,最短的路线是
线段的 计算 和差:如右图,M为线段AB上的点, 则AM+BM=AB,AM=AB-BM; 中点:如右图,若M是线段AB的中点, 则有AM= = AB
②
BM
考点 直线、线段、射线【省卷T6】
换算 1周角= °,1平角= °,1°= ',1'= ″
余角与 补角 余角:∠1+∠2=90° ∠1与∠2互为余角;
补角:∠1+∠2=180° ∠1与∠2互为补角;
性质: 同角(或等角)的余角 ,同角(或等角)的补角_________
360
180
60
60
相等
相等
考点 角的计算
对顶角 对顶角相等.如∠1与∠3,∠2与 ,∠5与 ,∠6与 .
邻补角 互为邻补角的两个角的和等于 .
如∠1与 或 .
三线 八角 同位角:“F”型,如∠1与∠5,∠2与∠6等;
内错角:“Z”型,如∠2与∠8,∠3与 ;
同旁内角:“U”型,如∠2与∠5,∠3与
∠4
∠7
∠8
180°
∠2
∠4
∠5
∠8
【以题理知】如右图①,直线a,b被直线c所截,形成8个角,对应填空.
考点 相交线与平行线【长沙T8】
垂线
的性质 (1)在同一平面内,过一点有且只有 条直线与已知直线垂直;
(2)直线外一点与直线上各点连接的所有线段中, 最短;
(3)点到直线的距离:从直线外一点到这条直线的垂线段的长度,
叫作点到直线的距离
一
垂线段
平行公理 及推论 基本事实:过直线外一点,有且只有一条直线
与这条直线平行;
推论:如果b∥a,c∥a,那么b∥c
判定
与性质 (1)同位角相等 两直线平行,如图①,旋转b,
若∠1=∠5,则a∥b;
(2)内错角相等 两直线平行,如图①,旋转b,
若∠2=∠8,则a∥b;
(3)同旁内角互补 两直线平行,如图①,旋转b,
若a∥b,则∠2+∠5=
180°
【以题理知】如右图①,直线a,b被直线c所截,形成8个角,对应填空.
考点 相交线与平行线【长沙T8】
重难精讲
变式探究
03
第四单元 第15讲
例1 (人教版七上P167习题T5改编)已知线段AB=4,在直线
AB上作线段BC,使得BC=2,若D是线段AC的中点,则线
段AD的长为( C )
A. 1 B. 3 C. 1或3 D. 2或3
C
分两种情况讨论
①点 C 在点B 的右侧
②点 C 在点B 的左侧
A
B
C
D
4
2
3
A
B
C
D
4
2
1
例2 (湘教版七上P165例4改编)如下图,AE平分∠CAD,
∠FAE=25°且与∠CAE互余,则∠CAD的度数是( A )
A. 130° B. 135°
C. 140° D. 125°
A
∠CAE=∠DAE
∠FAE+∠CAE=90°
∠CAE=65°
∠CAD=2∠CAE
∠CAD=2×65°=130°
2. 如图,直线AB,CD相交于点O,若∠1=80°26',
∠2=30°10',则∠AOE的度数为( B )
1. (2022·益阳)如图,PA,PB表示以点P为起点的两条公
路,其中公路PA的走向是南偏西34°,公路PB的走向是南偏
东56°,则这两条公路的夹角∠APB= °.
90
B
第2题图
A. 30°10'
B. 50°16'
C. 60°16'
D. 80°25'
第1题图
例3 如图,在△ABC中,点D,E在AB边上,点F在AC边上,EF∥DC,点H在BC边上,且∠CDH+∠CFE=180°.
求证:∠A=∠BDH. (请将下面的证明过程补充完整)
证明:∵EF∥DC,
∴∠CFE+ =180°
( ).
∵∠CDH+∠CFE=180°,
∴∠CDH= ( ).
∴ ∥_________
( ).
∴∠A=∠BDH.
∠FCD
两直线平行,同旁内角互补
∠FCD
等量代换
DH
AC
内错角相等,两直线平行
3. (2024·长沙)如图,在△ABC中,∠BAC=60°,
∠B=50°,AD∥BC,则∠1 的度数为( C )
A. 50° B. 60°
C. 70° D. 80°
第3题图
C
4. (2024·陕西)如图,AB∥DC,BC∥DE,∠B=145°,
则∠D的度数为( B )
A. 25° B. 35°
C. 45° D. 55°
第4题图
B
5. 如下图,小颖先画出了直线a,然后将含30°角的三角尺沿
着直尺的一边平移,依次画出了直线b,c.若∠1=70°,则
∠2的度数为( C )
A. 110° B. 70°
C. 40° D. 30°
第5题图
C
6. 【跨学科】(2024·深圳)如上图,一束平行光线照射平面镜后
反射,若入射光线与平面镜夹角∠1=50°,则反射光线与平
面镜夹角∠4的度数为 .
第6题图
【拓展设问】图中∠2的同旁内角一共有 个.
50°
3
课堂小结
线段、角、相交线与平行线
相交线与平行线
直线与线段
角及角平分线
线段的和与差
角的分类
两个基本事实
角度的换算
相交线
平行线
三线八角
余角和补角
角平分线
两点间的距离
线段的中点
直线、线段的相关计数
第15讲
图形初步与相交线、平行线
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第四单元 第15讲
课标要求 作业目标
几何图形初步 1.掌握线段、直线、射线、角的相关概念. 2.能计算和线段、角之间的数量关系. 3.能在综合性问题中,利用几何图形的知识解决一些简单的几何问题. 认识直线、射线、线段的概念、性质、表示和画法,会正确表述点与直线的关系
理解“两点确定一条直线”和“两点之间,线段最短”,理解并会度量两点间的距离,能解决简单的实际问题
了解角的概念、表示和画法,会用角度质量,认识度、分、秒并能进行简单的换算
会比较角的大小,理解角的和、差、角平分线,并会相关角度的计算
了解余角、补角的概念,知道余角、补角的性质并能解决简单的几何问题
要求与目标
课标要求 作业目标
相交线与平行线 1.理解对顶角、余角、补角等概念,探索并掌握对顶角相等、同角(或等角)的余角相等、同角(或等角)的补角相等的性质。 2.理解垂线、垂线段等概念,能用三角板或量角器过一点画已知直线的垂线。 3.掌握基本事实:同一平面内,过一点有且只有一条直线与已知直线垂直。 4.理解点到直线的距离的意义,能度量点到直线的距离。 5.识别同位角、内错角、同旁内角。 6.理解平行线的概念。掌握平行线基本事实I:过直线外一点有且只有一条直线与这条直线平行。 知道对顶角、互补角的概念,掌握对顶角相等、邻补角互补的性质
知道垂线、垂线段等概念,掌握垂线段最短的性质
了解点到直线的距离的意义,能解释基本事实:过一点有且只有一条直线与已知直线垂直
识别同位角、内错角、同旁内角
了解平行线概念,能解释平行公理及相关结论
掌握判定两条直线平行的三种方法及两条平行线的三个性质
要求与目标
接下表
课标要求 作业目标
相交线与平行线 7.掌握平行线基本事实ⅡI:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。 8.探索并证明平行线的判定定理:两条直线被第三条直线所截, 如果内错角相等(或同旁内角互补),那么这两条直线平行。 9.掌握平行线的性质定理I:两条平行直线被第三条直线所截,同位角相等。 10.探索并证明平行线的性质定理ⅡI:两条平行直线被第三条直线所截,内错角相等(或同旁内角互补)。 11.了解平行于同一条直线的两条直线平行 知道对顶角、互补角的概念,掌握对顶角相等、邻补角互补的性质
知道垂线、垂线段等概念,掌握垂线段最短的性质
了解点到直线的距离的意义,能解释基本事实:过一点有且只有一条直线与已知直线垂直
识别同位角、内错角、同旁内角
了解平行线概念,能解释平行公理及相关结论
掌握判定两条直线平行的三种方法及两条平行线的三个性质
要求与目标
接上表
教材整合 核心归纳
02
第四单元 第15讲
1. (2024·广西改编)已知∠1=35°,若∠1与∠2为对顶角,则
∠2= °;若∠1与∠3互补,则∠3= °.
2. (2024·甘孜州)如右图,已知AB∥CD,AD平分∠BAC,
∠1=30°,则∠2的度数是 .
35
145
30°
∠1=∠3=30°
3
∠2=∠3=30°
两个基 本事实 (1)两点确定一条直线; (2)两点之间,线段最短.如右图,最短的路线是
线段的 计算 和差:如右图,M为线段AB上的点, 则AM+BM=AB,AM=AB-BM; 中点:如右图,若M是线段AB的中点, 则有AM= = AB
②
BM
考点 直线、线段、射线【省卷T6】
换算 1周角= °,1平角= °,1°= ',1'= ″
余角与 补角 余角:∠1+∠2=90° ∠1与∠2互为余角;
补角:∠1+∠2=180° ∠1与∠2互为补角;
性质: 同角(或等角)的余角 ,同角(或等角)的补角_________
360
180
60
60
相等
相等
考点 角的计算
对顶角 对顶角相等.如∠1与∠3,∠2与 ,∠5与 ,∠6与 .
邻补角 互为邻补角的两个角的和等于 .
如∠1与 或 .
三线 八角 同位角:“F”型,如∠1与∠5,∠2与∠6等;
内错角:“Z”型,如∠2与∠8,∠3与 ;
同旁内角:“U”型,如∠2与∠5,∠3与
∠4
∠7
∠8
180°
∠2
∠4
∠5
∠8
【以题理知】如右图①,直线a,b被直线c所截,形成8个角,对应填空.
考点 相交线与平行线【长沙T8】
垂线
的性质 (1)在同一平面内,过一点有且只有 条直线与已知直线垂直;
(2)直线外一点与直线上各点连接的所有线段中, 最短;
(3)点到直线的距离:从直线外一点到这条直线的垂线段的长度,
叫作点到直线的距离
一
垂线段
平行公理 及推论 基本事实:过直线外一点,有且只有一条直线
与这条直线平行;
推论:如果b∥a,c∥a,那么b∥c
判定
与性质 (1)同位角相等 两直线平行,如图①,旋转b,
若∠1=∠5,则a∥b;
(2)内错角相等 两直线平行,如图①,旋转b,
若∠2=∠8,则a∥b;
(3)同旁内角互补 两直线平行,如图①,旋转b,
若a∥b,则∠2+∠5=
180°
【以题理知】如右图①,直线a,b被直线c所截,形成8个角,对应填空.
考点 相交线与平行线【长沙T8】
重难精讲
变式探究
03
第四单元 第15讲
例1 (人教版七上P167习题T5改编)已知线段AB=4,在直线
AB上作线段BC,使得BC=2,若D是线段AC的中点,则线
段AD的长为( C )
A. 1 B. 3 C. 1或3 D. 2或3
C
分两种情况讨论
①点 C 在点B 的右侧
②点 C 在点B 的左侧
A
B
C
D
4
2
3
A
B
C
D
4
2
1
例2 (湘教版七上P165例4改编)如下图,AE平分∠CAD,
∠FAE=25°且与∠CAE互余,则∠CAD的度数是( A )
A. 130° B. 135°
C. 140° D. 125°
A
∠CAE=∠DAE
∠FAE+∠CAE=90°
∠CAE=65°
∠CAD=2∠CAE
∠CAD=2×65°=130°
2. 如图,直线AB,CD相交于点O,若∠1=80°26',
∠2=30°10',则∠AOE的度数为( B )
1. (2022·益阳)如图,PA,PB表示以点P为起点的两条公
路,其中公路PA的走向是南偏西34°,公路PB的走向是南偏
东56°,则这两条公路的夹角∠APB= °.
90
B
第2题图
A. 30°10'
B. 50°16'
C. 60°16'
D. 80°25'
第1题图
例3 如图,在△ABC中,点D,E在AB边上,点F在AC边上,EF∥DC,点H在BC边上,且∠CDH+∠CFE=180°.
求证:∠A=∠BDH. (请将下面的证明过程补充完整)
证明:∵EF∥DC,
∴∠CFE+ =180°
( ).
∵∠CDH+∠CFE=180°,
∴∠CDH= ( ).
∴ ∥_________
( ).
∴∠A=∠BDH.
∠FCD
两直线平行,同旁内角互补
∠FCD
等量代换
DH
AC
内错角相等,两直线平行
3. (2024·长沙)如图,在△ABC中,∠BAC=60°,
∠B=50°,AD∥BC,则∠1 的度数为( C )
A. 50° B. 60°
C. 70° D. 80°
第3题图
C
4. (2024·陕西)如图,AB∥DC,BC∥DE,∠B=145°,
则∠D的度数为( B )
A. 25° B. 35°
C. 45° D. 55°
第4题图
B
5. 如下图,小颖先画出了直线a,然后将含30°角的三角尺沿
着直尺的一边平移,依次画出了直线b,c.若∠1=70°,则
∠2的度数为( C )
A. 110° B. 70°
C. 40° D. 30°
第5题图
C
6. 【跨学科】(2024·深圳)如上图,一束平行光线照射平面镜后
反射,若入射光线与平面镜夹角∠1=50°,则反射光线与平
面镜夹角∠4的度数为 .
第6题图
【拓展设问】图中∠2的同旁内角一共有 个.
50°
3
课堂小结
线段、角、相交线与平行线
相交线与平行线
直线与线段
角及角平分线
线段的和与差
角的分类
两个基本事实
角度的换算
相交线
平行线
三线八角
余角和补角
角平分线
两点间的距离
线段的中点
直线、线段的相关计数
同课章节目录
