第18讲 等腰三角形 2025年中考一轮数学专题复习课件(湖南)(共21张PPT)
文档属性
| 名称 | 第18讲 等腰三角形 2025年中考一轮数学专题复习课件(湖南)(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 951.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 22:14:00 | ||
图片预览








文档简介
(共21张PPT)
第18讲 等腰三角形
目录
CONTENTS
1
2
3
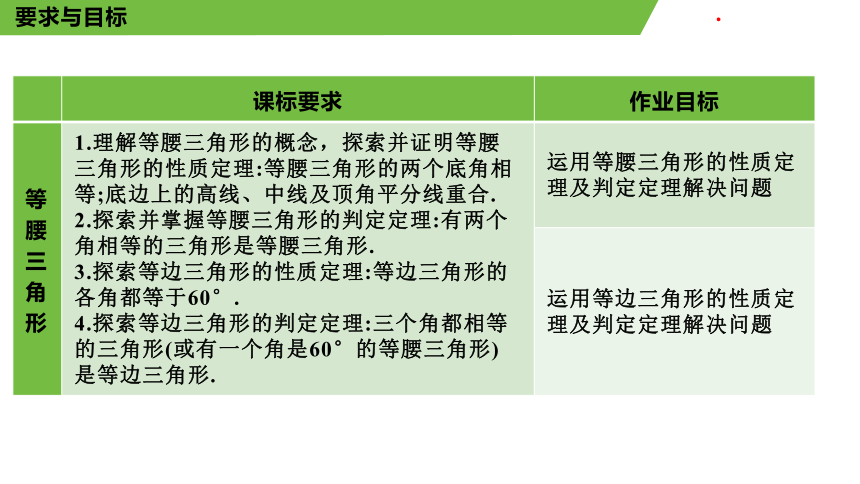
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第四单元 第18讲
课标要求 作业目标
等腰三角形 1.理解等腰三角形的概念,探索并证明等腰三角形的性质定理:等腰三角形的两个底角相等;底边上的高线、中线及顶角平分线重合. 2.探索并掌握等腰三角形的判定定理:有两个角相等的三角形是等腰三角形. 3.探索等边三角形的性质定理:等边三角形的各角都等于60°. 4.探索等边三角形的判定定理:三个角都相等的三角形(或有一个角是60°的等腰三角形)是等边三角形. 运用等腰三角形的性质定理及判定定理解决问题
运用等边三角形的性质定理及判定定理解决问题
要求与目标
教材整合 核心归纳
02
第四单元 第18讲
性
质 (1)两腰相等,两底角相等,即AB=AC, ∠B=∠C; (2)底边上的高、中线及顶角平分线重合,简称“三线合一”; (3)是轴对称图形,有一条对称轴
判
定 (1)定义法:有两条边相等的三角形是等腰三角形; (2)等角对等边:有两个角相等的三角形是等腰三角形 面
积 S= ah,其中a是底边长,h是底边上的高 考点 等腰三角形【省卷T14】
考点清单
2. 如右图,在△ABC中,∠B=∠C,DE⊥AB于点E,DE交BC于点D,连接AD.
第2题图
(1)若∠C=25°,则∠EDB= °;
(2)若AD=BD,BE=3,
则AC的长为 .
65
6
1. 已知等边三角形ABC的周长为12,点D是AB的中点,过
点D作BC边的平行线交AC于点E,
则DE的长是 .
2
A
B
C
D
E
BC=4
DE=BC=2
25°
25°
AB=AC=6
DE垂直平分AB
AB=2BE=6
性质 (1)三边相等,三个内角相等,且都等于60°; (2)是轴对称图形,有三条对称轴; (3)“三线合一”
判定 (1)定义法:三条边都相等的三角形是等边三角形; (2)三个角都相等的三角形是等边三角形; (3)有一个角是60°的等腰三角形是等边三角形 面积 S= ah= a2
性
质 线段垂直平分线上的点与这条线段两端点的距离相等.即如右图,若CD⊥AB于点O,点O为AB的中点, 则AP= ,∠A=
判
定 与线段两端点距离相等的点在这条线段的垂直平分线上.即如右图,若PA=PB,则点P在线段AB的垂直平分线上 BP
∠B
考点 等边三角形
考点 线段垂直平分线【长沙T19】
考点清单
重难精讲
变式探究
03
第四单元 第18讲
(2)若△ABC的一边长为3,一边长为4,
则△ABC的周长为 ;
例 如下图,在△ABC中,AB=AC,点D为边BC上一点,E为边AC上一点,连接AD,DE.
例题图
(1) 如图①,若∠BAC=56°,∠BAD=36°,AD=AE,则∠B的度数为 ,
∠EDC的度数为 ;
62°
18°
10或11
56°
36°
∠B=∠C
62°
∠B=∠C=(180°-∠BAC)=62°
∠AED=∠ADE=80°
80°
62°
∠EDC=∠AED-∠C=18°
分类讨论思想
3,3,4 或 4,4,3
20°
例 如下图,在△ABC中,AB=AC,点D为边BC上一点,E为边AC上一点,连接AD,DE.
(3)如图②,若∠ABC=60°,AB=8,点D为边BC的中点,
点E为边AC的中点,则∠BAD的度数为 ,DE的长为 ;
30°
4
等边三角形
三线合一
中位线
(4) 如图②,若AD是△ABC的中线,DE∥AB,
求证:△ADE为等腰三角形.
证明:∵AB=AC,AD是△ABC的中线,
∴∠BAD=∠CAD.
又∵DE∥AB,
∴∠BAD=∠ADE.
∴∠CAD=∠ADE.
∴EA=ED.
∴△ADE为等腰三角形.
三线合一
求证边相等
求证角相等
等边对等角
∠BAC=60°
∠BAD=∠DAC
DE=AB
2. (2024·云南)已知AF是等腰三角形ABC底边BC上的高,若
点F到直线AB的距离为3,则点F到直线AC的距离为( C )
1. (2024·湖南)若等腰三角形的一个底角的度数为40°,则它的
顶角的度数为 °.
100
【易错变式】若等腰三角形的一个内角为70°,则另外两个内
角的度数分别为 .
A. B. 2 C. 3 D.
70°,40°或55°,55°
C
3. 如图,在△ABC中,AB=6cm,AC=4cm,
BD平分∠ABC,CD平分∠ACB,EF过点D且EF∥BC,
则△AEF的周长是( C )
A. 8cm B. 9cm
第3题图
C
C. 10cm D. 11cm
△AEF的周长=AE+EF+AF
=AE+ED+DF+AF
=AE+EB+CF+AF
=AB+AC
=10 cm
4. 如下图,点D,E在△ABC的边BC上,AD=AE,BD=CE.
(1)求证:AB=AC;
第4题图
证明:如图,过点A作AF⊥BC于点F.
∵AD=AE,
∴DF=EF.
∵BD=CE,
∴BF=CF.
∴AB=AC.
(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC
与△ADE外所有的等腰三角形.
解:除△ABC与△ADE外所有的等腰三角形有△ABD,
△AEC,△ABE,△ADC.
F
做辅助线
三线合一
DF=EF
AB=AC
5. 如图,AB∥CD,△ACE为等边三角形,
∠DCE=40°,则∠EAB等于( C )
A. 40° B. 30°
C. 20° D. 15°
第5题图
C
6. 将含30°角的直角三角板和直尺按如图所示的方式放置,
已知∠α=60°,点B,C表示的刻度分别
为1cm,3cm,则线段AB的长为 cm.
第6题图
2
7. (2024·凉山州改编)如下图,在△ABC中,分别以点A和点C
为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作
直线MN,交BC于点D,连接AD. 若△ABD的周长为50cm,
则AB+BC=( C )
A. 25cm B. 45cm
C. 50cm D. 55cm
第7题图
C
【变式设问】若∠B=50°,∠C=35°,
则∠BAD的度数为 .
60°
△ABD的周长=AB+AD+BD
=AB+CD+BD
=AB+BC
35°
35°
70°
50°
DN是线段 AC 的垂直平分线
8. 如图,在△ABC中,∠ACB=90°,BC=3,AE=5,
AB的垂直平分线DE交AB于点D,交AC于点E,
则CE= .
第8题图
4
BE=AE=5
3
5
5
勾股定理
CE==4
9. (2024·自贡)如图,等边三角形ABC钢架的立柱
CD⊥AB于点D,AB长12m.现将钢架立柱缩短成DE,
∠BED=60°,则新钢架减少用钢( D )
A. (24-12 )m B. (24-8 )m
C. (24-6 )m D. (24-4 )m
第9题图
D
10. 在如图所示的正方形网格中,网格线的交点称为格点.已
知点A,B是两格点,若点C也是图中的格点,且
使得△ABC为等腰三角形,则点C的个数是( )
A. 6 B. 7 C. 8 D. 9
第10题图
C
11. 如下图,点C是线段AB上除点A,B外的任意一点,分别以AC,BC为边在线段AB的同侧作等边三角形ACD和等边三角形BCE,连接AE交DC于点M,连接BD交CE于点N,连接MN. 求证:
(1)AE=BD;
第11题图
证明:∵△ACD和△BCE是等边三角形,
∴AC=DC,CE=CB,
∠DCA=∠ECB=60°.
∴∠DCA+∠DCE=∠ECB+∠DCE.
∴∠ACE=∠DCB.
在△ACE与△DCB中,
∴△ACE≌△DCB(SAS).
∴AE=BD.
(2)△CMN为等边三角形.
第11题图
证明:由(1)知△ACE≌△DCB,
∴∠CAE=CDB.
∵∠DCN=180°-∠ACM-∠ECB=60°,
∴∠DCN=∠ACM.
又∵AC=DC,
∴△ACM≌△DCN(ASA).
∴CM=CN.
∵∠MCN=60°,MC=NC,
∴△CMN为等边三角形.
11. 如下图,点C是线段AB上除点A,B外的任意一点,分别以AC,BC为边在线段AB的同侧作等边三角形ACD和等边三角形BCE,连接AE交DC于点M,连接BD交CE于点N,连接MN. 求证:
课堂小结
等腰三角形
等腰三角形的性质与判定
等边三角形的性质与判定
线段的垂直平分线
等腰三角形
等腰三角形的定义
等边三角形
等边三角形的定义
线段的垂直平分线的定义
线段的垂直平分线的性质与判定
第18讲 等腰三角形
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第四单元 第18讲
课标要求 作业目标
等腰三角形 1.理解等腰三角形的概念,探索并证明等腰三角形的性质定理:等腰三角形的两个底角相等;底边上的高线、中线及顶角平分线重合. 2.探索并掌握等腰三角形的判定定理:有两个角相等的三角形是等腰三角形. 3.探索等边三角形的性质定理:等边三角形的各角都等于60°. 4.探索等边三角形的判定定理:三个角都相等的三角形(或有一个角是60°的等腰三角形)是等边三角形. 运用等腰三角形的性质定理及判定定理解决问题
运用等边三角形的性质定理及判定定理解决问题
要求与目标
教材整合 核心归纳
02
第四单元 第18讲
性
质 (1)两腰相等,两底角相等,即AB=AC, ∠B=∠C; (2)底边上的高、中线及顶角平分线重合,简称“三线合一”; (3)是轴对称图形,有一条对称轴
判
定 (1)定义法:有两条边相等的三角形是等腰三角形; (2)等角对等边:有两个角相等的三角形是等腰三角形 面
积 S= ah,其中a是底边长,h是底边上的高 考点 等腰三角形【省卷T14】
考点清单
2. 如右图,在△ABC中,∠B=∠C,DE⊥AB于点E,DE交BC于点D,连接AD.
第2题图
(1)若∠C=25°,则∠EDB= °;
(2)若AD=BD,BE=3,
则AC的长为 .
65
6
1. 已知等边三角形ABC的周长为12,点D是AB的中点,过
点D作BC边的平行线交AC于点E,
则DE的长是 .
2
A
B
C
D
E
BC=4
DE=BC=2
25°
25°
AB=AC=6
DE垂直平分AB
AB=2BE=6
性质 (1)三边相等,三个内角相等,且都等于60°; (2)是轴对称图形,有三条对称轴; (3)“三线合一”
判定 (1)定义法:三条边都相等的三角形是等边三角形; (2)三个角都相等的三角形是等边三角形; (3)有一个角是60°的等腰三角形是等边三角形 面积 S= ah= a2
性
质 线段垂直平分线上的点与这条线段两端点的距离相等.即如右图,若CD⊥AB于点O,点O为AB的中点, 则AP= ,∠A=
判
定 与线段两端点距离相等的点在这条线段的垂直平分线上.即如右图,若PA=PB,则点P在线段AB的垂直平分线上 BP
∠B
考点 等边三角形
考点 线段垂直平分线【长沙T19】
考点清单
重难精讲
变式探究
03
第四单元 第18讲
(2)若△ABC的一边长为3,一边长为4,
则△ABC的周长为 ;
例 如下图,在△ABC中,AB=AC,点D为边BC上一点,E为边AC上一点,连接AD,DE.
例题图
(1) 如图①,若∠BAC=56°,∠BAD=36°,AD=AE,则∠B的度数为 ,
∠EDC的度数为 ;
62°
18°
10或11
56°
36°
∠B=∠C
62°
∠B=∠C=(180°-∠BAC)=62°
∠AED=∠ADE=80°
80°
62°
∠EDC=∠AED-∠C=18°
分类讨论思想
3,3,4 或 4,4,3
20°
例 如下图,在△ABC中,AB=AC,点D为边BC上一点,E为边AC上一点,连接AD,DE.
(3)如图②,若∠ABC=60°,AB=8,点D为边BC的中点,
点E为边AC的中点,则∠BAD的度数为 ,DE的长为 ;
30°
4
等边三角形
三线合一
中位线
(4) 如图②,若AD是△ABC的中线,DE∥AB,
求证:△ADE为等腰三角形.
证明:∵AB=AC,AD是△ABC的中线,
∴∠BAD=∠CAD.
又∵DE∥AB,
∴∠BAD=∠ADE.
∴∠CAD=∠ADE.
∴EA=ED.
∴△ADE为等腰三角形.
三线合一
求证边相等
求证角相等
等边对等角
∠BAC=60°
∠BAD=∠DAC
DE=AB
2. (2024·云南)已知AF是等腰三角形ABC底边BC上的高,若
点F到直线AB的距离为3,则点F到直线AC的距离为( C )
1. (2024·湖南)若等腰三角形的一个底角的度数为40°,则它的
顶角的度数为 °.
100
【易错变式】若等腰三角形的一个内角为70°,则另外两个内
角的度数分别为 .
A. B. 2 C. 3 D.
70°,40°或55°,55°
C
3. 如图,在△ABC中,AB=6cm,AC=4cm,
BD平分∠ABC,CD平分∠ACB,EF过点D且EF∥BC,
则△AEF的周长是( C )
A. 8cm B. 9cm
第3题图
C
C. 10cm D. 11cm
△AEF的周长=AE+EF+AF
=AE+ED+DF+AF
=AE+EB+CF+AF
=AB+AC
=10 cm
4. 如下图,点D,E在△ABC的边BC上,AD=AE,BD=CE.
(1)求证:AB=AC;
第4题图
证明:如图,过点A作AF⊥BC于点F.
∵AD=AE,
∴DF=EF.
∵BD=CE,
∴BF=CF.
∴AB=AC.
(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC
与△ADE外所有的等腰三角形.
解:除△ABC与△ADE外所有的等腰三角形有△ABD,
△AEC,△ABE,△ADC.
F
做辅助线
三线合一
DF=EF
AB=AC
5. 如图,AB∥CD,△ACE为等边三角形,
∠DCE=40°,则∠EAB等于( C )
A. 40° B. 30°
C. 20° D. 15°
第5题图
C
6. 将含30°角的直角三角板和直尺按如图所示的方式放置,
已知∠α=60°,点B,C表示的刻度分别
为1cm,3cm,则线段AB的长为 cm.
第6题图
2
7. (2024·凉山州改编)如下图,在△ABC中,分别以点A和点C
为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作
直线MN,交BC于点D,连接AD. 若△ABD的周长为50cm,
则AB+BC=( C )
A. 25cm B. 45cm
C. 50cm D. 55cm
第7题图
C
【变式设问】若∠B=50°,∠C=35°,
则∠BAD的度数为 .
60°
△ABD的周长=AB+AD+BD
=AB+CD+BD
=AB+BC
35°
35°
70°
50°
DN是线段 AC 的垂直平分线
8. 如图,在△ABC中,∠ACB=90°,BC=3,AE=5,
AB的垂直平分线DE交AB于点D,交AC于点E,
则CE= .
第8题图
4
BE=AE=5
3
5
5
勾股定理
CE==4
9. (2024·自贡)如图,等边三角形ABC钢架的立柱
CD⊥AB于点D,AB长12m.现将钢架立柱缩短成DE,
∠BED=60°,则新钢架减少用钢( D )
A. (24-12 )m B. (24-8 )m
C. (24-6 )m D. (24-4 )m
第9题图
D
10. 在如图所示的正方形网格中,网格线的交点称为格点.已
知点A,B是两格点,若点C也是图中的格点,且
使得△ABC为等腰三角形,则点C的个数是( )
A. 6 B. 7 C. 8 D. 9
第10题图
C
11. 如下图,点C是线段AB上除点A,B外的任意一点,分别以AC,BC为边在线段AB的同侧作等边三角形ACD和等边三角形BCE,连接AE交DC于点M,连接BD交CE于点N,连接MN. 求证:
(1)AE=BD;
第11题图
证明:∵△ACD和△BCE是等边三角形,
∴AC=DC,CE=CB,
∠DCA=∠ECB=60°.
∴∠DCA+∠DCE=∠ECB+∠DCE.
∴∠ACE=∠DCB.
在△ACE与△DCB中,
∴△ACE≌△DCB(SAS).
∴AE=BD.
(2)△CMN为等边三角形.
第11题图
证明:由(1)知△ACE≌△DCB,
∴∠CAE=CDB.
∵∠DCN=180°-∠ACM-∠ECB=60°,
∴∠DCN=∠ACM.
又∵AC=DC,
∴△ACM≌△DCN(ASA).
∴CM=CN.
∵∠MCN=60°,MC=NC,
∴△CMN为等边三角形.
11. 如下图,点C是线段AB上除点A,B外的任意一点,分别以AC,BC为边在线段AB的同侧作等边三角形ACD和等边三角形BCE,连接AE交DC于点M,连接BD交CE于点N,连接MN. 求证:
课堂小结
等腰三角形
等腰三角形的性质与判定
等边三角形的性质与判定
线段的垂直平分线
等腰三角形
等腰三角形的定义
等边三角形
等边三角形的定义
线段的垂直平分线的定义
线段的垂直平分线的性质与判定
同课章节目录
