第19讲 直角三角形 2025年中考一轮数学专题复习课件(湖南)(共27张PPT)
文档属性
| 名称 | 第19讲 直角三角形 2025年中考一轮数学专题复习课件(湖南)(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
第19讲 直角三角形
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第四单元 第19讲
课标要求 作业目标
直角三角形 1.理解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余,直角三角形斜边上的中线等于斜边的一半. 2.掌握有两个角互余的三角形是直角三角形 掌握直角三角形的两个锐角互余和有两个角互余的三角形是直角三角形
掌握直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余,直角三角形斜边上的中线等于斜边的一半.
要求与目标
课标要求 作业目标
勾股定理及其逆定理 探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问题 认识勾股定理及其逆定理的重要意义,知道这两个定理的联系与区别
会用勾股定理及其逆定理解决一些简单的几何问题
能用勾股定理及其逆定理解决一些简单的实际问题
能在综合的实际问题情境中抽象出数学模型,建立形数之间的联系
要求与目标
教材整合 核心归纳
02
第四单元 第19讲
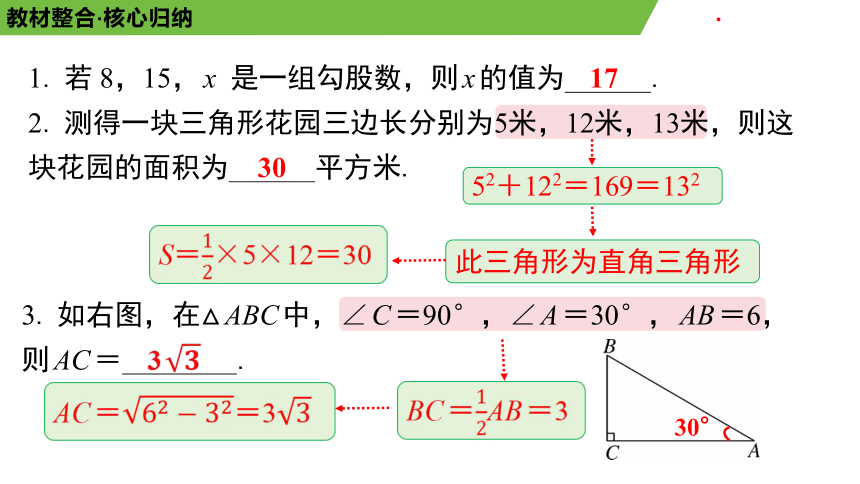
3. 如右图,在△ABC中,∠C=90°,∠A=30°,AB=6,
则AC= .
1. 若 8,15,x 是一组勾股数,则x的值为 .
2. 测得一块三角形花园三边长分别为5米,12米,13米,则这
块花园的面积为 平方米.
17
30
3
52+122=169=132
此三角形为直角三角形
S=×5×12=30
BC=AB=3
30°
AC==3
勾股定理 直角三角形的两条直角边长分别为a,b,斜边长为c,则有
逆定理 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形为直角三角形.若a2+b2=c2且a,b,c均为正整数,则称a,b,c为一组勾股数.
如3,4,5;6,8,10;5,12,13;7,24,25等
a2+b2=c2
考点 勾股定理及其逆定理【省卷T22,长沙T9,T19】
考点清单
定义 有一个角是90°的三角形叫作直角三角形
性质
(1)直角三角形的两锐角之和等于 ;
(2)直角三角形斜边上的中线等于 ,
如左图,CD= AB;
(3)勾股定理: ;(4)在直角三角形中,若一个锐角等于30°,那么它所对的直角边等于 .
如左图,三角形的三边之比为1∶ ∶2
判定 (1)定义法:有一个角是直角的三角形是直角三角形;
(2)勾股定理逆定理;(3)有两个角 的三角形是直角三角形;(4)一条边上的中线等于这条边的一半的三角形是直角三角形(应用时需先证明)
90°
斜边的一半
a2+b2=c2
斜边的一半
互余
考点 直角三角形【省卷T18,长沙T10,T19】
考点清单
面积 S= ab= ch,其中a,b分别为两条直角边长,c为斜边长,h为斜边上的高 特殊直角三角形(等腰直角三角形) 性质:两锐角相等且都等于45°;三角形的三边之比为1∶1∶ ; 面积:S= a2= c2,其中a为直角边长,c为斜边长 典型 应用 已知等腰直角三角形ABC,一般通过作垂线构造一线三等角解题.
结论:△ACE≌△CBF→
EF=AE+BF
考点 直角三角形【省卷T18,长沙T10,T19】
考点清单
重难精讲
变式探究
03
第四单元 第19讲
例 如下图①,在Rt△ABC中,∠ACB=90°,点D是AB边上一点,连接CD.
(1)若∠B=45°,AB=2 ,则AC= .
(2)若点D是AB边的中点.
①当∠B=25°时,∠ACD= °;
②当AC=3,BC=4 时,CD= .
(3)若CD⊥AB,AC=6,BC=8,
则S△ABC= ,CD= .
2
65
24
等腰直角三角形三边之比为1∶1∶
CD= AB=BD
25°
25°
AB=5
S△ABC=×AC×BC=×AB×CD
D
(4)如下图②,在Rt△ABC中,∠ACB=90°,若点D是BC上的一点,连接AD,AC=5,BC=12,将△ABC沿AD折叠,使点C落在边AB上的点E处.
求折痕AD的长.
解:∵∠C=90°,AC=5,BC=12,∴AB=13.
设CD=x,则DE=x,AE=5,BE=8,BD=12-x.
∵∠AED=∠C=90°,
∴在Rt△EBD中,x2+82=(12-x)2,解得x= .
∴AD= = .
AB=13
△ACD≌△AED
12
5
5
x
方程思想
x
设CD=x
AC=AE=5,
CD=ED=x
构建方程
1. 直角三角形的两条边长分别为3和4,则这个直角三角形的第
三边长为( C )
A. 5 B. C. 5或 D.
C
2. 如下图,以直角三角形的三边为边,分别向外作等边三角
形、半圆、等腰直角三角形和正方形,下列四种情况的面积关
系满足S1+S2=S3的图形有( D )
A. 1个 B. 2个 C. 3个 D. 4个
第2题图
D
3. 如下图,在4×4的正方形网格中,点A,B,C都在格点
上,则∠ABC=( C )
A. 30° B. 40°
C. 45° D. 60°
第3题图
C
1
3
2
4
BC2+AC2=20
AB2=20
△ABC是等腰直角三角形
构造直角三角形
4. (2024·吉林)如下图①中有一首古算诗,根据诗中的描述可以
计算出红莲所在位置的湖水深度,其示意图如下图②,其中
AB=AB',AB⊥B'C于点C,BC=0.5尺,B'C=2尺.设AC的
长度为x尺,可列方程为 .
第4题图
x2+22=(x+0.5)2
x
x+0.5
2
5. (2023·株洲)一技术人员用刻度尺(单位:cm)测量某三角形部
件的尺寸.如右图所示,已知∠ACB=90°,点D为边AB的中
点,点A,B对应的刻度分别为1cm,7cm,
则CD=( B )
A. 3.5cm B. 3cm
C. 4.5cm D. 6cm
第5题图
B
6. 下列条件中,能够判断△ABC为直角三角形的是( A )
A. AB=6,BC=8,AC=10
B. AB∶BC∶AC=2∶3∶4
C. ∠A=∠B=∠C
D. ∠A∶∠B∶∠C=3∶4∶5
A
7. 如下图,在Rt△ABC中,∠BAC=90°,点D为边BC上的
点,AD⊥BC.
第7题图
(1)若∠B=55°,
则∠CAD的度数为 ;
(2)若∠B=45°,BD=4,
则S△ABC的面积为 .
55°
16
∠B+∠BAD=90°
∠CAD+∠BAD=90°
∠B=∠CAD
S△ABC=2S△ABD=2××BD×AD=16
△BAD,△ADC是等腰直角三角形
BD=AD=DC=4
BC=8
8. 如图,CD为Rt△ABC斜边AB上的中线,
点E为边AC的中点.
第8题图
(1)若AC=8,CD=5,
则DE= ;
(2)若∠A=35°,
则∠CDE的度数为 .
3
55°
9. 如下图,在Rt△ACB中,∠ACB=90°,点M为边AB的中点,点E在线段AM上,EF⊥AC于点F,连接CM,CE. 已知∠A=50°,∠ACE=30°.
(1)求证:CE=CM;
第9题图
证明:∵∠ACB=90°,点M为边AB的中点,
∴MC=MA=MB.
∴∠MCA=∠A=50°.
∴∠MCB=∠B=40°.
∴∠EMC=∠MCB+∠B=80°.
∵∠ACE=30°,∴∠MEC=∠A+∠ACE=80°.
∴∠MEC=∠EMC. ∴CE=CM.
(2)若AB=4,求线段FC的长.
(2)解:∵AB=4,∴CE=CM= AB=2.
∵EF⊥AC,∠ACE=30°,
∴EF= CE=1.∴FC= .
解:∵AB=4,∴CE=CM= AB=2.
∵EF⊥AC,∠ACE=30°,
∴EF= CE=1.∴FC= .
10. △ABC的三边长a,b,c满足(a-b)2+ +
|c-3 |=0,则△ABC是( D )
A. 等腰三角形 B. 直角三角形
C. 锐角三角形 D. 等腰直角三角形
D
11. (2024·新疆)如下图,在Rt△ABC中,∠C=90°,
∠A=30°,AB=8.若点D在直线AB上(不与点A,B重合),
且∠BCD=30°,则AD的长为 .
第11题图
6或12
12. 如图,已知△ABC中,AB=AC,∠BAC=90°,直角
∠EDF的顶点D是边BC的中点,两边DE,DF分别交边
AB,AC于点E,F. 若BE=1,CF= ,则DE= .
第12题图
【方法提示】在等腰直角三角形ABC中,点D为边BC的中
点,DE⊥DF,一般要连接斜边中线 .
结论:△CDF≌△ ,△DEF为 三角形.
AD
ADE
等腰直角
13. 如下图①,点O为线段AD上一点,CO⊥AD于点O,且
OA=OB,OC=OD,点M,N分别是边AC,BD的中点,
连接OM,ON,MN.
(1)求证:AC=BD;
证明:∵CO⊥AD,∴∠AOC=∠DOB=90°.
∵OA=OB,OC=OD,
∴△AOC≌△BOD(SAS).∴AC=BD.
(2)试判断△MON的形状,并说明理由;
13. 如下图①,点O为线段AD上一点,CO⊥AD于点O,且OA=OB,
OC=OD,点M,N分别是边AC,BD的中点,连接OM,ON,MN.
解:△MON是等腰直角三角形.理由:
∵AM=CM,BN=ND,∠AOC=∠DOB=90°,
∴OM= AC,ON= BD.
∵△AOC≌△BOD,∴∠C=∠D,AC=BD.
∴OM=ON. ∵OM=CM,ON=ND,
∴∠C=∠MOC,∠D=∠NOD.
∴∠MOC=∠NOD. ∴∠MON=∠COD=90°.
∴△MON是等腰直角三角形.
(3)若AC=2,在下图②中,点M在DB的延长线上,求△AMD的面积.
13. 如下图①,点O为线段AD上一点,CO⊥AD于点O,且OA=OB,
OC=OD,点M,N分别是边AC,BD的中点,连接OM,ON,MN.
解:解法一:如图②,连接AB.
∵△AOC≌△BOD,∴∠C=∠D.
∵∠CBM=∠OBD,∴∠CMB=∠DOB=90°.
∴MB⊥AC. ∵MA=CM,∴BC=BA.
∵△MON是等腰直角三角形,
∴∠MNO=45°=∠D+∠NOD.
∵NO=ND,∴∠NOD=∠D=22.5°.
∴∠C=∠BAC=22.5°.
∴∠ABO=∠C+∠BAC=45°.
∵AO=OB,设OA=OB=a,
∴AB=BC= a.
在Rt△AOC中,∵AC2=OA2+OC2,
∴4=a2+(a+ a)2.∴a2=2- .
∵OM=ON,∠MOC=∠NOD,OC=OD,
∴△MOC≌△NOD(SAS).
∴S△AMD=S△AOM+S△MON+S△NOD=S△AMO+S△MOC+S△MON
=S△AOC+S△MON= ·a·(a+ a)+ ×1×1= .
解法二:由直角三角形斜边上的中线性质直接求得
AM=OM=ON=ND=1,
再由Rt△OMN得MN= ,
∵△AOC≌△BOD,
∴∠C=∠D.
∵∠CBM=∠OBD,∴∠CMB=∠DOB=90°.
∴MB⊥AC. ∴S△AMD= AM·DM= .
(3)若AC=2,在下图②中,点M在DB的延长线上,求△AMD的面积.
13. 如下图①,点O为线段AD上一点,CO⊥AD于点O,且OA=OB,
OC=OD,点M,N分别是边AC,BD的中点,连接OM,ON,MN.
【辅助设问】通过(1)中全等可得∠C=∠D,进而可得△AMD
为 三角形.°.AC=BD.
直角
课堂小结
直角三角形
性质
判定
边
角
边
角
互逆定理
勾股定理
勾股定理的逆定理
第19讲 直角三角形
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第四单元 第19讲
课标要求 作业目标
直角三角形 1.理解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余,直角三角形斜边上的中线等于斜边的一半. 2.掌握有两个角互余的三角形是直角三角形 掌握直角三角形的两个锐角互余和有两个角互余的三角形是直角三角形
掌握直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余,直角三角形斜边上的中线等于斜边的一半.
要求与目标
课标要求 作业目标
勾股定理及其逆定理 探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问题 认识勾股定理及其逆定理的重要意义,知道这两个定理的联系与区别
会用勾股定理及其逆定理解决一些简单的几何问题
能用勾股定理及其逆定理解决一些简单的实际问题
能在综合的实际问题情境中抽象出数学模型,建立形数之间的联系
要求与目标
教材整合 核心归纳
02
第四单元 第19讲
3. 如右图,在△ABC中,∠C=90°,∠A=30°,AB=6,
则AC= .
1. 若 8,15,x 是一组勾股数,则x的值为 .
2. 测得一块三角形花园三边长分别为5米,12米,13米,则这
块花园的面积为 平方米.
17
30
3
52+122=169=132
此三角形为直角三角形
S=×5×12=30
BC=AB=3
30°
AC==3
勾股定理 直角三角形的两条直角边长分别为a,b,斜边长为c,则有
逆定理 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形为直角三角形.若a2+b2=c2且a,b,c均为正整数,则称a,b,c为一组勾股数.
如3,4,5;6,8,10;5,12,13;7,24,25等
a2+b2=c2
考点 勾股定理及其逆定理【省卷T22,长沙T9,T19】
考点清单
定义 有一个角是90°的三角形叫作直角三角形
性质
(1)直角三角形的两锐角之和等于 ;
(2)直角三角形斜边上的中线等于 ,
如左图,CD= AB;
(3)勾股定理: ;(4)在直角三角形中,若一个锐角等于30°,那么它所对的直角边等于 .
如左图,三角形的三边之比为1∶ ∶2
判定 (1)定义法:有一个角是直角的三角形是直角三角形;
(2)勾股定理逆定理;(3)有两个角 的三角形是直角三角形;(4)一条边上的中线等于这条边的一半的三角形是直角三角形(应用时需先证明)
90°
斜边的一半
a2+b2=c2
斜边的一半
互余
考点 直角三角形【省卷T18,长沙T10,T19】
考点清单
面积 S= ab= ch,其中a,b分别为两条直角边长,c为斜边长,h为斜边上的高 特殊直角三角形(等腰直角三角形) 性质:两锐角相等且都等于45°;三角形的三边之比为1∶1∶ ; 面积:S= a2= c2,其中a为直角边长,c为斜边长 典型 应用 已知等腰直角三角形ABC,一般通过作垂线构造一线三等角解题.
结论:△ACE≌△CBF→
EF=AE+BF
考点 直角三角形【省卷T18,长沙T10,T19】
考点清单
重难精讲
变式探究
03
第四单元 第19讲
例 如下图①,在Rt△ABC中,∠ACB=90°,点D是AB边上一点,连接CD.
(1)若∠B=45°,AB=2 ,则AC= .
(2)若点D是AB边的中点.
①当∠B=25°时,∠ACD= °;
②当AC=3,BC=4 时,CD= .
(3)若CD⊥AB,AC=6,BC=8,
则S△ABC= ,CD= .
2
65
24
等腰直角三角形三边之比为1∶1∶
CD= AB=BD
25°
25°
AB=5
S△ABC=×AC×BC=×AB×CD
D
(4)如下图②,在Rt△ABC中,∠ACB=90°,若点D是BC上的一点,连接AD,AC=5,BC=12,将△ABC沿AD折叠,使点C落在边AB上的点E处.
求折痕AD的长.
解:∵∠C=90°,AC=5,BC=12,∴AB=13.
设CD=x,则DE=x,AE=5,BE=8,BD=12-x.
∵∠AED=∠C=90°,
∴在Rt△EBD中,x2+82=(12-x)2,解得x= .
∴AD= = .
AB=13
△ACD≌△AED
12
5
5
x
方程思想
x
设CD=x
AC=AE=5,
CD=ED=x
构建方程
1. 直角三角形的两条边长分别为3和4,则这个直角三角形的第
三边长为( C )
A. 5 B. C. 5或 D.
C
2. 如下图,以直角三角形的三边为边,分别向外作等边三角
形、半圆、等腰直角三角形和正方形,下列四种情况的面积关
系满足S1+S2=S3的图形有( D )
A. 1个 B. 2个 C. 3个 D. 4个
第2题图
D
3. 如下图,在4×4的正方形网格中,点A,B,C都在格点
上,则∠ABC=( C )
A. 30° B. 40°
C. 45° D. 60°
第3题图
C
1
3
2
4
BC2+AC2=20
AB2=20
△ABC是等腰直角三角形
构造直角三角形
4. (2024·吉林)如下图①中有一首古算诗,根据诗中的描述可以
计算出红莲所在位置的湖水深度,其示意图如下图②,其中
AB=AB',AB⊥B'C于点C,BC=0.5尺,B'C=2尺.设AC的
长度为x尺,可列方程为 .
第4题图
x2+22=(x+0.5)2
x
x+0.5
2
5. (2023·株洲)一技术人员用刻度尺(单位:cm)测量某三角形部
件的尺寸.如右图所示,已知∠ACB=90°,点D为边AB的中
点,点A,B对应的刻度分别为1cm,7cm,
则CD=( B )
A. 3.5cm B. 3cm
C. 4.5cm D. 6cm
第5题图
B
6. 下列条件中,能够判断△ABC为直角三角形的是( A )
A. AB=6,BC=8,AC=10
B. AB∶BC∶AC=2∶3∶4
C. ∠A=∠B=∠C
D. ∠A∶∠B∶∠C=3∶4∶5
A
7. 如下图,在Rt△ABC中,∠BAC=90°,点D为边BC上的
点,AD⊥BC.
第7题图
(1)若∠B=55°,
则∠CAD的度数为 ;
(2)若∠B=45°,BD=4,
则S△ABC的面积为 .
55°
16
∠B+∠BAD=90°
∠CAD+∠BAD=90°
∠B=∠CAD
S△ABC=2S△ABD=2××BD×AD=16
△BAD,△ADC是等腰直角三角形
BD=AD=DC=4
BC=8
8. 如图,CD为Rt△ABC斜边AB上的中线,
点E为边AC的中点.
第8题图
(1)若AC=8,CD=5,
则DE= ;
(2)若∠A=35°,
则∠CDE的度数为 .
3
55°
9. 如下图,在Rt△ACB中,∠ACB=90°,点M为边AB的中点,点E在线段AM上,EF⊥AC于点F,连接CM,CE. 已知∠A=50°,∠ACE=30°.
(1)求证:CE=CM;
第9题图
证明:∵∠ACB=90°,点M为边AB的中点,
∴MC=MA=MB.
∴∠MCA=∠A=50°.
∴∠MCB=∠B=40°.
∴∠EMC=∠MCB+∠B=80°.
∵∠ACE=30°,∴∠MEC=∠A+∠ACE=80°.
∴∠MEC=∠EMC. ∴CE=CM.
(2)若AB=4,求线段FC的长.
(2)解:∵AB=4,∴CE=CM= AB=2.
∵EF⊥AC,∠ACE=30°,
∴EF= CE=1.∴FC= .
解:∵AB=4,∴CE=CM= AB=2.
∵EF⊥AC,∠ACE=30°,
∴EF= CE=1.∴FC= .
10. △ABC的三边长a,b,c满足(a-b)2+ +
|c-3 |=0,则△ABC是( D )
A. 等腰三角形 B. 直角三角形
C. 锐角三角形 D. 等腰直角三角形
D
11. (2024·新疆)如下图,在Rt△ABC中,∠C=90°,
∠A=30°,AB=8.若点D在直线AB上(不与点A,B重合),
且∠BCD=30°,则AD的长为 .
第11题图
6或12
12. 如图,已知△ABC中,AB=AC,∠BAC=90°,直角
∠EDF的顶点D是边BC的中点,两边DE,DF分别交边
AB,AC于点E,F. 若BE=1,CF= ,则DE= .
第12题图
【方法提示】在等腰直角三角形ABC中,点D为边BC的中
点,DE⊥DF,一般要连接斜边中线 .
结论:△CDF≌△ ,△DEF为 三角形.
AD
ADE
等腰直角
13. 如下图①,点O为线段AD上一点,CO⊥AD于点O,且
OA=OB,OC=OD,点M,N分别是边AC,BD的中点,
连接OM,ON,MN.
(1)求证:AC=BD;
证明:∵CO⊥AD,∴∠AOC=∠DOB=90°.
∵OA=OB,OC=OD,
∴△AOC≌△BOD(SAS).∴AC=BD.
(2)试判断△MON的形状,并说明理由;
13. 如下图①,点O为线段AD上一点,CO⊥AD于点O,且OA=OB,
OC=OD,点M,N分别是边AC,BD的中点,连接OM,ON,MN.
解:△MON是等腰直角三角形.理由:
∵AM=CM,BN=ND,∠AOC=∠DOB=90°,
∴OM= AC,ON= BD.
∵△AOC≌△BOD,∴∠C=∠D,AC=BD.
∴OM=ON. ∵OM=CM,ON=ND,
∴∠C=∠MOC,∠D=∠NOD.
∴∠MOC=∠NOD. ∴∠MON=∠COD=90°.
∴△MON是等腰直角三角形.
(3)若AC=2,在下图②中,点M在DB的延长线上,求△AMD的面积.
13. 如下图①,点O为线段AD上一点,CO⊥AD于点O,且OA=OB,
OC=OD,点M,N分别是边AC,BD的中点,连接OM,ON,MN.
解:解法一:如图②,连接AB.
∵△AOC≌△BOD,∴∠C=∠D.
∵∠CBM=∠OBD,∴∠CMB=∠DOB=90°.
∴MB⊥AC. ∵MA=CM,∴BC=BA.
∵△MON是等腰直角三角形,
∴∠MNO=45°=∠D+∠NOD.
∵NO=ND,∴∠NOD=∠D=22.5°.
∴∠C=∠BAC=22.5°.
∴∠ABO=∠C+∠BAC=45°.
∵AO=OB,设OA=OB=a,
∴AB=BC= a.
在Rt△AOC中,∵AC2=OA2+OC2,
∴4=a2+(a+ a)2.∴a2=2- .
∵OM=ON,∠MOC=∠NOD,OC=OD,
∴△MOC≌△NOD(SAS).
∴S△AMD=S△AOM+S△MON+S△NOD=S△AMO+S△MOC+S△MON
=S△AOC+S△MON= ·a·(a+ a)+ ×1×1= .
解法二:由直角三角形斜边上的中线性质直接求得
AM=OM=ON=ND=1,
再由Rt△OMN得MN= ,
∵△AOC≌△BOD,
∴∠C=∠D.
∵∠CBM=∠OBD,∴∠CMB=∠DOB=90°.
∴MB⊥AC. ∴S△AMD= AM·DM= .
(3)若AC=2,在下图②中,点M在DB的延长线上,求△AMD的面积.
13. 如下图①,点O为线段AD上一点,CO⊥AD于点O,且OA=OB,
OC=OD,点M,N分别是边AC,BD的中点,连接OM,ON,MN.
【辅助设问】通过(1)中全等可得∠C=∠D,进而可得△AMD
为 三角形.°.AC=BD.
直角
课堂小结
直角三角形
性质
判定
边
角
边
角
互逆定理
勾股定理
勾股定理的逆定理
同课章节目录
