第22讲 多边形与平行四边形 2025年中考一轮数学专题复习课件(湖南)(共26张PPT)
文档属性
| 名称 | 第22讲 多边形与平行四边形 2025年中考一轮数学专题复习课件(湖南)(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 22:15:09 | ||
图片预览








文档简介
(共26张PPT)
第22讲
多边形与平行四边形
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第五单元 第22讲
课标要求 作业目标
多边形与平行四边形 1.了解多边形的概念了解四边形及多边形的顶点、边、内角、外角与对角线;探究多边形的内角和与外角和公式.2.理解两平行线之间距离的概念,能度量两平行线之间的距离.3.理解平行四边形的概念,了解四边形的不稳定性. 4.探索并证明平行四边形的性质定理及判定定理. 掌握平行四边形的概念及性质定理,并能运用它们解决几何证明问题和简单的实际问题
了解两平行线之间距离的意义,会度量两平行线之间的距离
掌握平行四边形的判定定理,并能运用它们解决几何证明问题和简单的实际问题
掌握三角形的中位线定理,能解释三角形中位线定理的证明方法
了解多边形的概念及多边形的顶点、边、内角、外角与对角线;
掌握多边形内角和与外角和公式。
要求与目标
教材整合 核心归纳
02
第五单元 第22讲
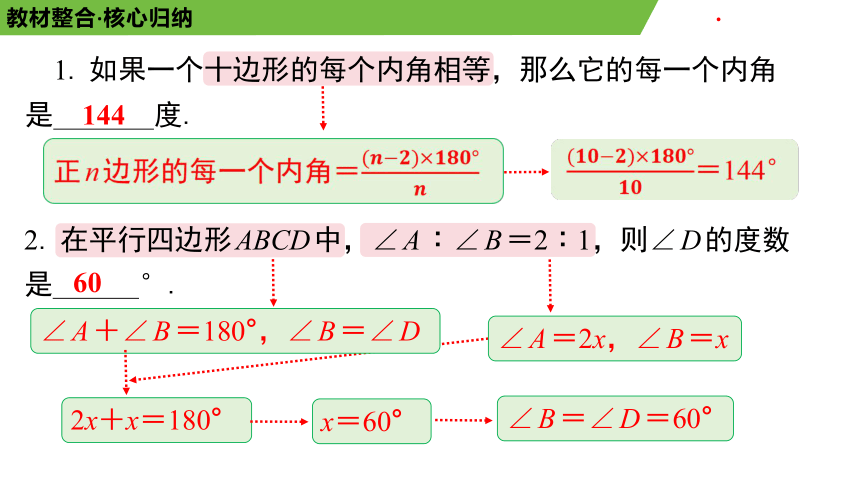
1. 如果一个十边形的每个内角相等,那么它的每一个内角
是 度.
144
60
2. 在平行四边形ABCD中,∠A∶∠B=2∶1,则∠D的度数
是 °.
正n边形的每一个内角=
=144°
∠A+∠B=180°,∠B=∠D
∠B=∠D=60°
∠A=2x,∠B=x
2x+x=180°
x=60°
操作2:将两根木棒的中点处钉上钉子,如图②,转动木棒,顺次连接木棒的端点得到四边形ABCD,则四边形ABCD为
形.
3. 操作1:将两个全等的三角形纸片按图①所示方式拼成一
个四边形ABCD,则四边形ABCD为 形;
第3题图
平行四边
平行四边
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
梯形 梯形是指只有一组对边平行的四边形【2022课标新增】
多边
形 内角和定理:n 边形的内角和等于 ;
外角和定理:n边形的外角和都等于 ;
对角线:过n边形的每一个顶点可以引 条对角线,n边形共有 条对角线
(n-2)×180°
360°
(n-3)
考点 梯形的概念与多边形的性质【省卷T6】
正多
边形 定义:各边 ,各角也 的多边形叫作正多边形;
对称轴:正n边形有 条对称轴;
内外角:正n边形的每一个内角都等于 ,每一个外角都等于
相等
相等
n
考点清单
定义 两组对边分别平行的四边形叫作平行四边形
性
质 边:两组对边平行且相等,即下图①中,AB CD,AD ;
角:两组对角分别相等,即下图①中,∠DAB= ,∠ABC=∠ADC;
对角线:对角线互相平分,即下图①中,AO=CO,
BO= ;
对称性:是中心对称图形;
面积:S=底×高,即下图①中,S=AB· ;
如下图②,S1=S2,S3=S4;如下图③,S1+S2=S3;
如下图④, =
BC
∠DCB
DO
DE
考点 平行四边形的性质与判定【省卷T22,长沙T23,T24】
考点清单
判
定 判定方法 几何语言
两组对边分别平行 ∵AB∥CD, ,
∴四边形ABCD是平行四边形
AD∥BC
判
定 两组对边分别相等 ∵AB=CD, ,
∴四边形ABCD是平行四边形
一组对边平行且相等 ∵AB∥CD, ,
∴四边形ABCD是平行四边形
两组对角分别相等 ∵∠DAB=∠DCB, ,
∴四边形ABCD是平行四边形
对角线互相平分 ∵AO=CO, ,
∴四边形ABCD是平行四边形
AD=BC
AB=CD
∠ABC=∠ADC
BO=DO
考点 平行四边形的性质与判定【省卷T22,长沙T23,T24】
考点清单
重难精讲
变式探究
03
第五单元 第22讲
例 改编问题链 如图①,点E,F是平行四边形ABCD对角线上的两点,给出下列三个条件:①BE=DF;
②AF=CE;③∠AEB=∠CFD.
(1)从上述三个条件中选择一个,能够使四边形AECF
是平行四边形的条件有 (填序号).
①③
例题图①
AB∥CD
AB=CD
∠ABD=∠CDB
①BE=DF
△ABE≌△CDF
③∠AEB
=∠CFD
+
AE=CF
同理可证△DFA≌△BEC
AF=EC
△ABE≌△CDF
AE=CF
∠AED=∠CFE
AE∥CF
四边形AECF
是平行四边形
(2)从(1)中选择一个加以证明.
解法一:选择条件 (填序号);
例题图①
①
例 改编问题链 如图①,点E,F是平行四边形ABCD对
角线上的两点,给出下列三个条件:①BE=DF;②AF=
CE;③∠AEB=∠CFD.
证明:∵四边形ABCD是平行四边形,∴AB=CD,
AB∥CD. ∴∠ABE=∠CDF.
又∵BE=DF,∴△BEA≌△DFC(SAS).∴AE=FC.
同理可证△DFA≌△BEC(SAS),
从而得AF=EC. ∴四边形AECF是平行四边形.
解法二:选择条件 (填序号).
证明略.
③
证明略.
(3)如图②,在 ABCD中,若AE⊥BD于点E,CF⊥BD于
点F,AE=3,EF=2,求AC的长.
例题图②
解:如图,设AC交BD于点O.
易得四边形AECF为平行四边形,
在Rt△AEO中,
AO= = .
∴AC=2AO=2 .
∴OE=OF= EF=1,AO=OC.
O
类比(1)中③易得,
四边形AECF为平行四边形
运用勾股定理求AO的长
(4)如下图③,在 ABCD中,若BE=EF=DF,在不添加任
何辅助线的情况下,请直接写出图中所有面积
与四边形AECF面积相等的三角形.
例题图③
解:△ABF,△ADE,△CBF,△CDE.
类比(1)中①易得,
四边形AECF为平行四边形
S AECF=2S△AEF=2S△CEF
根据同底等高,S△AEF=S△ABE=S△AFD=S△CEF=S△BEC=S△CFD
1. 一个多边形外角和是内角和的 ,则这个多边形的边数为 .
2. 如图,在正五边形ABCDE中,连接AC,
那么∠BAC的度数为 .
第2题图
11
36°
3. (2024·遂宁)佩佩在“黄娥古镇”研学时学习扎染技术,得到一个内角和为1080°的正多边形图案,这个正多边形的每个外角为( C )
A. 36° B. 40°
C. 45° D. 60°
(n-2)×180°=1080°
C
n=8
=
4. (2023·邵阳)如图,在四边形ABCD中,AB∥CD,若添加一个条件,使四边形ABCD为平行四边形,则下列正确的是( )
A. AD=BC B. ∠ABD=∠BDC
C. AB=AD D. ∠A=∠C
第4题图
D
5. (2024·广州)如图, ABCD中,BC=2,点E在DA的延长线上,BE=3.若BA平分∠EBC,则DE= .
5
第5题图
6. 如图,在 ABCD中,AD=10,对角线AC与BD相交于
点O,AC+BD=22,则△BOC的周长为 .
第6题图
【变式题】在 ABCD中,已知AC+BD=22,
则AD长度的取值范围为 .
21
0<AD<11
BO+OC=(AC+BD)
BO+OC=11
BC=AD=10
△BOC的周长=21
△BOC的周长=BO+OC+BC
三角形的任意两边之和大于第三边
7. (2023·长沙)如下图,在 ABCD中,DF平分∠ADC,交
BC于点E,交AB的延长线于点F.
(1)求证:AD=AF;
证明:在 ABCD中,∵AB∥CD,
∴∠CDE=∠F.
∵DF平分∠ADC,
∴∠ADE=∠CDE.
∴∠F=∠ADF.
∴AD=AF.
平行四边形+内角平分线,可得等腰三角形.
(2)若AD=6,AB=3,∠A=120°,求BF的长度和△ADF的
面积.
7. (2023·长沙)如下图,在 ABCD中,DF平分∠ADC,交
BC于点E,交AB的延长线于点F.
解:∵AD=AF=6,AB=3,
∴BF=AF-AB=3.
如图,过点D作DH⊥AF交FA的延长线于点H,
∵∠BAD=120°,∴∠DAH=60°.
∴∠ADH=30°.∴AH= AD=3.
∴DH= =3 .
∴△ADF的面积= AF·DH= ×6×3 =9 .
8. (2024·湖南)如下图,在四边形ABCD中,AB∥CD,点E在边AB上, .
请从“①∠B=∠AED;②AE=BE,AE=CD”这两组条件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形BCDE为平行四边形;
①(或②)
证明如下:
∵∠B=∠AED,
∴BC∥DE.
∵AB∥CD,
∴四边形BCDE为平行四边形.
或选择②.证明如下:
∵AE=BE,AE=CD,
∴BE=CD.
∵AB∥CD,
∴四边形BCDE为平行四边形.
第8题图
BC∥DE
BE=CD
(2)若AD⊥AB,AD=8,BC=10,求线段AE的长.
第8题图
解:由(1)可知,
四边形BCDE为平行四边形,
∴DE=BC=10.
∵AD⊥AB,∴∠A=90°.
∴AE= = =6.
即线段AE的长为6.
四边形BCDE为平行四边形
8
10
10
DE=BC=10
勾股定理AE==6
9. (2024·赤峰)如下图是正n边形纸片的一部分,其中l,m是
正n边形两条边的一部分,若l,m所在的直线相交形成的锐角
为60°,则n的值是( B )
A. 5
B. 6
C. 8
D. 10
第9题图
B
10. 如下图,在 ABCD中,O是对角线AC,BD的交点,过
点O的直线分别交AD,BC于点M,N. 若△CON的面积为
3,△DOM的面积为5,则 ABCD的面积是( C )
A. 16 B. 24 C. 32 D. 40
第10题图
C
11. 已知平面直角坐标系xOy内,点A,C的坐标分别是(3,0),(1,2).
第11题图
(1)如图,四边形ABCO为平行四边形,则顶点B的坐标
为 ;
(4,2)
(2)【易错变式】若以A,B,C,O四点构成的四边形为平行
四边形,则点B的坐标为 .
(4,2)或(-2,2)或(2,-2)
课堂小结
多边形与平行四边形
多边形
n边形的性质
平行四边形
定义
性质
判定
正n边形的性质
第22讲
多边形与平行四边形
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第五单元 第22讲
课标要求 作业目标
多边形与平行四边形 1.了解多边形的概念了解四边形及多边形的顶点、边、内角、外角与对角线;探究多边形的内角和与外角和公式.2.理解两平行线之间距离的概念,能度量两平行线之间的距离.3.理解平行四边形的概念,了解四边形的不稳定性. 4.探索并证明平行四边形的性质定理及判定定理. 掌握平行四边形的概念及性质定理,并能运用它们解决几何证明问题和简单的实际问题
了解两平行线之间距离的意义,会度量两平行线之间的距离
掌握平行四边形的判定定理,并能运用它们解决几何证明问题和简单的实际问题
掌握三角形的中位线定理,能解释三角形中位线定理的证明方法
了解多边形的概念及多边形的顶点、边、内角、外角与对角线;
掌握多边形内角和与外角和公式。
要求与目标
教材整合 核心归纳
02
第五单元 第22讲
1. 如果一个十边形的每个内角相等,那么它的每一个内角
是 度.
144
60
2. 在平行四边形ABCD中,∠A∶∠B=2∶1,则∠D的度数
是 °.
正n边形的每一个内角=
=144°
∠A+∠B=180°,∠B=∠D
∠B=∠D=60°
∠A=2x,∠B=x
2x+x=180°
x=60°
操作2:将两根木棒的中点处钉上钉子,如图②,转动木棒,顺次连接木棒的端点得到四边形ABCD,则四边形ABCD为
形.
3. 操作1:将两个全等的三角形纸片按图①所示方式拼成一
个四边形ABCD,则四边形ABCD为 形;
第3题图
平行四边
平行四边
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
梯形 梯形是指只有一组对边平行的四边形【2022课标新增】
多边
形 内角和定理:n 边形的内角和等于 ;
外角和定理:n边形的外角和都等于 ;
对角线:过n边形的每一个顶点可以引 条对角线,n边形共有 条对角线
(n-2)×180°
360°
(n-3)
考点 梯形的概念与多边形的性质【省卷T6】
正多
边形 定义:各边 ,各角也 的多边形叫作正多边形;
对称轴:正n边形有 条对称轴;
内外角:正n边形的每一个内角都等于 ,每一个外角都等于
相等
相等
n
考点清单
定义 两组对边分别平行的四边形叫作平行四边形
性
质 边:两组对边平行且相等,即下图①中,AB CD,AD ;
角:两组对角分别相等,即下图①中,∠DAB= ,∠ABC=∠ADC;
对角线:对角线互相平分,即下图①中,AO=CO,
BO= ;
对称性:是中心对称图形;
面积:S=底×高,即下图①中,S=AB· ;
如下图②,S1=S2,S3=S4;如下图③,S1+S2=S3;
如下图④, =
BC
∠DCB
DO
DE
考点 平行四边形的性质与判定【省卷T22,长沙T23,T24】
考点清单
判
定 判定方法 几何语言
两组对边分别平行 ∵AB∥CD, ,
∴四边形ABCD是平行四边形
AD∥BC
判
定 两组对边分别相等 ∵AB=CD, ,
∴四边形ABCD是平行四边形
一组对边平行且相等 ∵AB∥CD, ,
∴四边形ABCD是平行四边形
两组对角分别相等 ∵∠DAB=∠DCB, ,
∴四边形ABCD是平行四边形
对角线互相平分 ∵AO=CO, ,
∴四边形ABCD是平行四边形
AD=BC
AB=CD
∠ABC=∠ADC
BO=DO
考点 平行四边形的性质与判定【省卷T22,长沙T23,T24】
考点清单
重难精讲
变式探究
03
第五单元 第22讲
例 改编问题链 如图①,点E,F是平行四边形ABCD对角线上的两点,给出下列三个条件:①BE=DF;
②AF=CE;③∠AEB=∠CFD.
(1)从上述三个条件中选择一个,能够使四边形AECF
是平行四边形的条件有 (填序号).
①③
例题图①
AB∥CD
AB=CD
∠ABD=∠CDB
①BE=DF
△ABE≌△CDF
③∠AEB
=∠CFD
+
AE=CF
同理可证△DFA≌△BEC
AF=EC
△ABE≌△CDF
AE=CF
∠AED=∠CFE
AE∥CF
四边形AECF
是平行四边形
(2)从(1)中选择一个加以证明.
解法一:选择条件 (填序号);
例题图①
①
例 改编问题链 如图①,点E,F是平行四边形ABCD对
角线上的两点,给出下列三个条件:①BE=DF;②AF=
CE;③∠AEB=∠CFD.
证明:∵四边形ABCD是平行四边形,∴AB=CD,
AB∥CD. ∴∠ABE=∠CDF.
又∵BE=DF,∴△BEA≌△DFC(SAS).∴AE=FC.
同理可证△DFA≌△BEC(SAS),
从而得AF=EC. ∴四边形AECF是平行四边形.
解法二:选择条件 (填序号).
证明略.
③
证明略.
(3)如图②,在 ABCD中,若AE⊥BD于点E,CF⊥BD于
点F,AE=3,EF=2,求AC的长.
例题图②
解:如图,设AC交BD于点O.
易得四边形AECF为平行四边形,
在Rt△AEO中,
AO= = .
∴AC=2AO=2 .
∴OE=OF= EF=1,AO=OC.
O
类比(1)中③易得,
四边形AECF为平行四边形
运用勾股定理求AO的长
(4)如下图③,在 ABCD中,若BE=EF=DF,在不添加任
何辅助线的情况下,请直接写出图中所有面积
与四边形AECF面积相等的三角形.
例题图③
解:△ABF,△ADE,△CBF,△CDE.
类比(1)中①易得,
四边形AECF为平行四边形
S AECF=2S△AEF=2S△CEF
根据同底等高,S△AEF=S△ABE=S△AFD=S△CEF=S△BEC=S△CFD
1. 一个多边形外角和是内角和的 ,则这个多边形的边数为 .
2. 如图,在正五边形ABCDE中,连接AC,
那么∠BAC的度数为 .
第2题图
11
36°
3. (2024·遂宁)佩佩在“黄娥古镇”研学时学习扎染技术,得到一个内角和为1080°的正多边形图案,这个正多边形的每个外角为( C )
A. 36° B. 40°
C. 45° D. 60°
(n-2)×180°=1080°
C
n=8
=
4. (2023·邵阳)如图,在四边形ABCD中,AB∥CD,若添加一个条件,使四边形ABCD为平行四边形,则下列正确的是( )
A. AD=BC B. ∠ABD=∠BDC
C. AB=AD D. ∠A=∠C
第4题图
D
5. (2024·广州)如图, ABCD中,BC=2,点E在DA的延长线上,BE=3.若BA平分∠EBC,则DE= .
5
第5题图
6. 如图,在 ABCD中,AD=10,对角线AC与BD相交于
点O,AC+BD=22,则△BOC的周长为 .
第6题图
【变式题】在 ABCD中,已知AC+BD=22,
则AD长度的取值范围为 .
21
0<AD<11
BO+OC=(AC+BD)
BO+OC=11
BC=AD=10
△BOC的周长=21
△BOC的周长=BO+OC+BC
三角形的任意两边之和大于第三边
7. (2023·长沙)如下图,在 ABCD中,DF平分∠ADC,交
BC于点E,交AB的延长线于点F.
(1)求证:AD=AF;
证明:在 ABCD中,∵AB∥CD,
∴∠CDE=∠F.
∵DF平分∠ADC,
∴∠ADE=∠CDE.
∴∠F=∠ADF.
∴AD=AF.
平行四边形+内角平分线,可得等腰三角形.
(2)若AD=6,AB=3,∠A=120°,求BF的长度和△ADF的
面积.
7. (2023·长沙)如下图,在 ABCD中,DF平分∠ADC,交
BC于点E,交AB的延长线于点F.
解:∵AD=AF=6,AB=3,
∴BF=AF-AB=3.
如图,过点D作DH⊥AF交FA的延长线于点H,
∵∠BAD=120°,∴∠DAH=60°.
∴∠ADH=30°.∴AH= AD=3.
∴DH= =3 .
∴△ADF的面积= AF·DH= ×6×3 =9 .
8. (2024·湖南)如下图,在四边形ABCD中,AB∥CD,点E在边AB上, .
请从“①∠B=∠AED;②AE=BE,AE=CD”这两组条件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形BCDE为平行四边形;
①(或②)
证明如下:
∵∠B=∠AED,
∴BC∥DE.
∵AB∥CD,
∴四边形BCDE为平行四边形.
或选择②.证明如下:
∵AE=BE,AE=CD,
∴BE=CD.
∵AB∥CD,
∴四边形BCDE为平行四边形.
第8题图
BC∥DE
BE=CD
(2)若AD⊥AB,AD=8,BC=10,求线段AE的长.
第8题图
解:由(1)可知,
四边形BCDE为平行四边形,
∴DE=BC=10.
∵AD⊥AB,∴∠A=90°.
∴AE= = =6.
即线段AE的长为6.
四边形BCDE为平行四边形
8
10
10
DE=BC=10
勾股定理AE==6
9. (2024·赤峰)如下图是正n边形纸片的一部分,其中l,m是
正n边形两条边的一部分,若l,m所在的直线相交形成的锐角
为60°,则n的值是( B )
A. 5
B. 6
C. 8
D. 10
第9题图
B
10. 如下图,在 ABCD中,O是对角线AC,BD的交点,过
点O的直线分别交AD,BC于点M,N. 若△CON的面积为
3,△DOM的面积为5,则 ABCD的面积是( C )
A. 16 B. 24 C. 32 D. 40
第10题图
C
11. 已知平面直角坐标系xOy内,点A,C的坐标分别是(3,0),(1,2).
第11题图
(1)如图,四边形ABCO为平行四边形,则顶点B的坐标
为 ;
(4,2)
(2)【易错变式】若以A,B,C,O四点构成的四边形为平行
四边形,则点B的坐标为 .
(4,2)或(-2,2)或(2,-2)
课堂小结
多边形与平行四边形
多边形
n边形的性质
平行四边形
定义
性质
判定
正n边形的性质
同课章节目录
